L. Pandolfi
Lezioni di Analisi Matematica 2
Il testo presenta tre blocchi principali di argomenti:
A
Successioni e serie numeriche e di funzioni:
Cap.
1, e
2.
B
Questa parte consta di due, da studiarsi
in sequenza.
B1 Funzioni di più variabili
e integrazione (multipla, di curva e
di superficie): Cap.
3–
8.
B2 Campi
conservativi,Cap.
9.
C
Sistemi di equazioni differenziali: Cap.
10.
Lo studio dei blocchi A e B può scambiarsi di ordine senza problemi. Invece, è
consigliabile studiare C per ultimo. Infatti, lo studio del Cap. 10 richiede il
concetto di continuità e differenziabilità di funzioni di più variabili, studiato ai
paragrafi 4.1–4.2. Ovunque nello studio del Cap. 10 è necessario conoscere il
concetto di curva (ma non le proprietà differenziali delle curve, né gli integrali di
curva). L’esponenziale di matrici richiede la definizione di serie, Cap. 1, e 2 e il
paragrafo 10.4 richiede il Cap. 9.
Indice
Elenco delle figure
1.1 Il test di MacLaurin1.2
a sinistra, a
destra 1.3
a sinistra, a
destra 1.4 a
sinistra e a
destra2.1 Distanza
2.2 Le distanze
e 2.3 Convergenza
uniforme e convergenza in media2.4 La convergenza uniforme non implica
la convergenza della successione delle derivate2.5 Gli intervalli che si
usano nella dimostrazione del teorema di Abel2.6 Somme parziali della
serie (2.3) (a sinistra e della serie (2.4) (a destra)2.7 Somma parziali della
serie (2.5)2.8 Illustrazione del Teorema 83 2.9 Estensione per periodicità
della funzione (2.32)2.10 Il fenomeno di Gibbs 2.11 Le serie di Fourier delle
restrizioni a
di (sinistra
sopra ), di (destra
sopra), di
(sinistra sotto) e di (destra
sotto) 3.1 Insieme connesso, a sinistra, e convesso a destra. 3.2 Senso
positivo di rotazione e verso sugli assi coordinati3.3 Sfera di centro
l’origine in norme diverse3.4 Teorema di Pitagora e identità
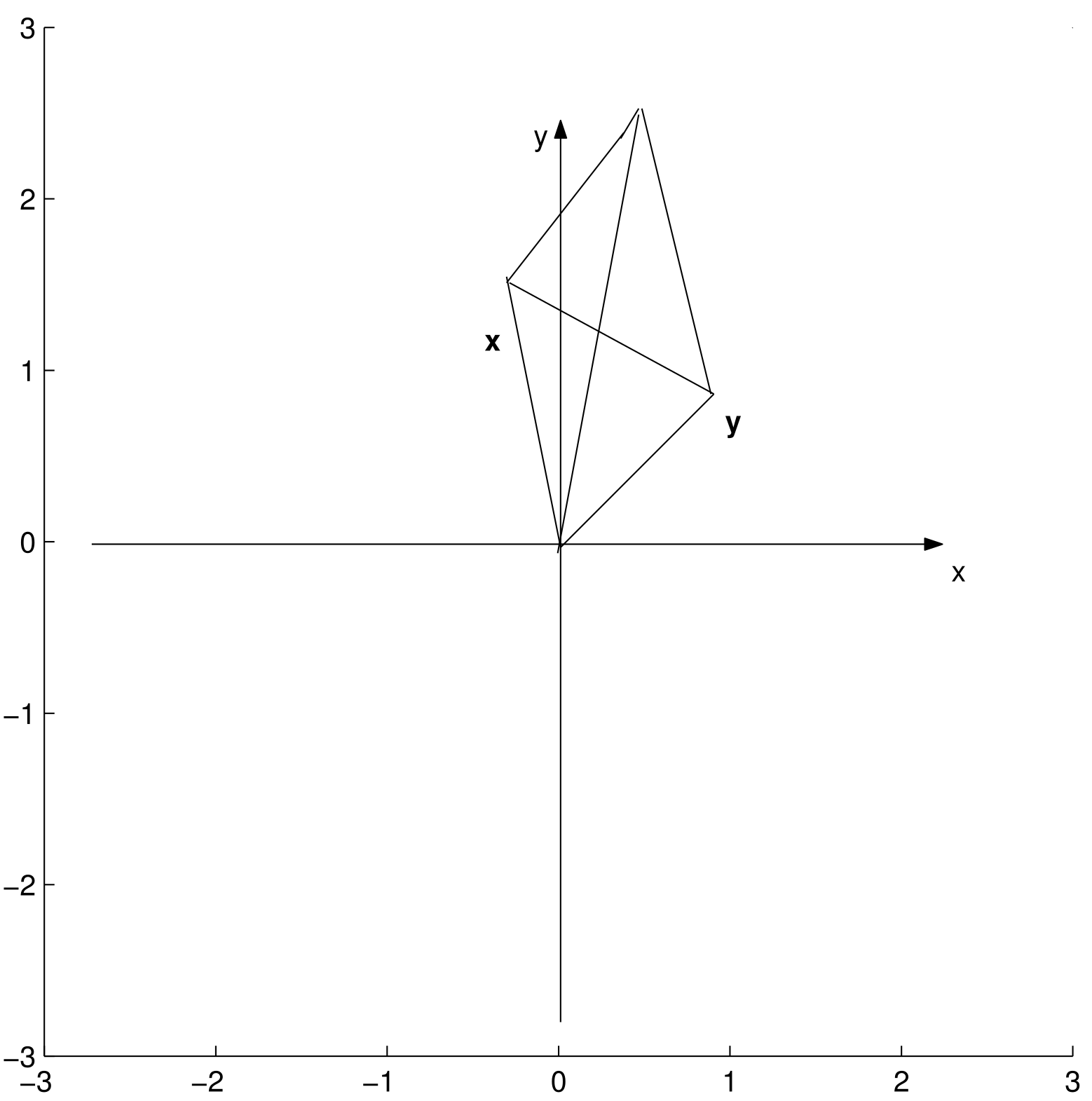
del parallelogramma 3.5 Calcolo dell’area di un parallelogramma
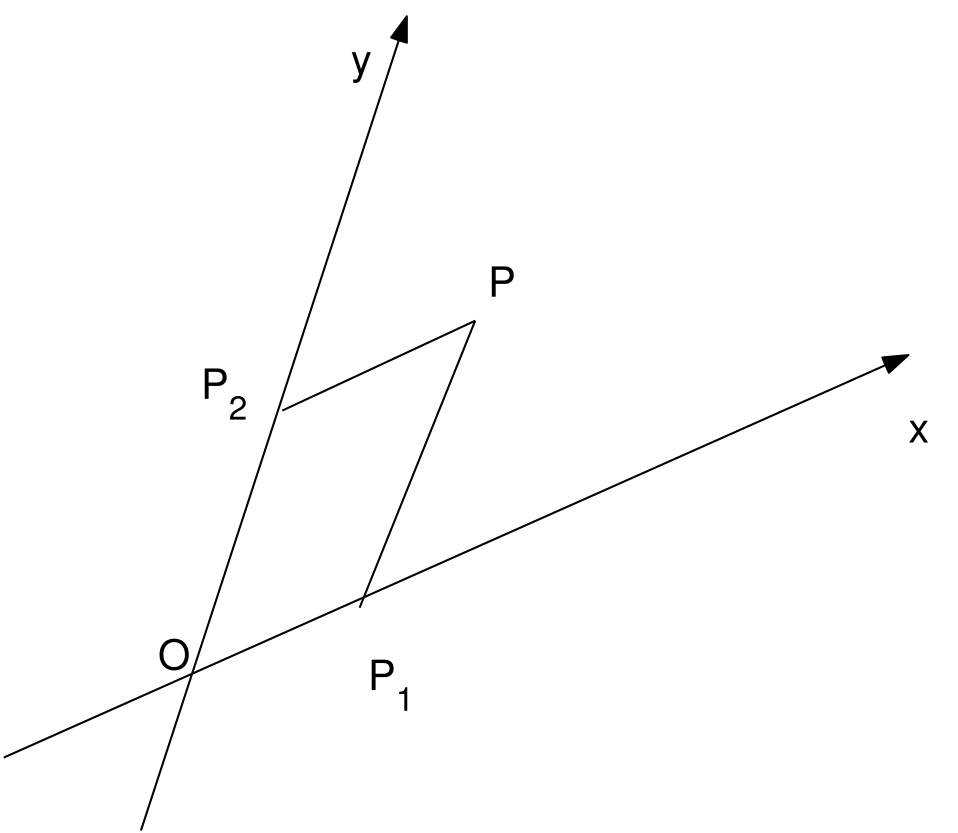
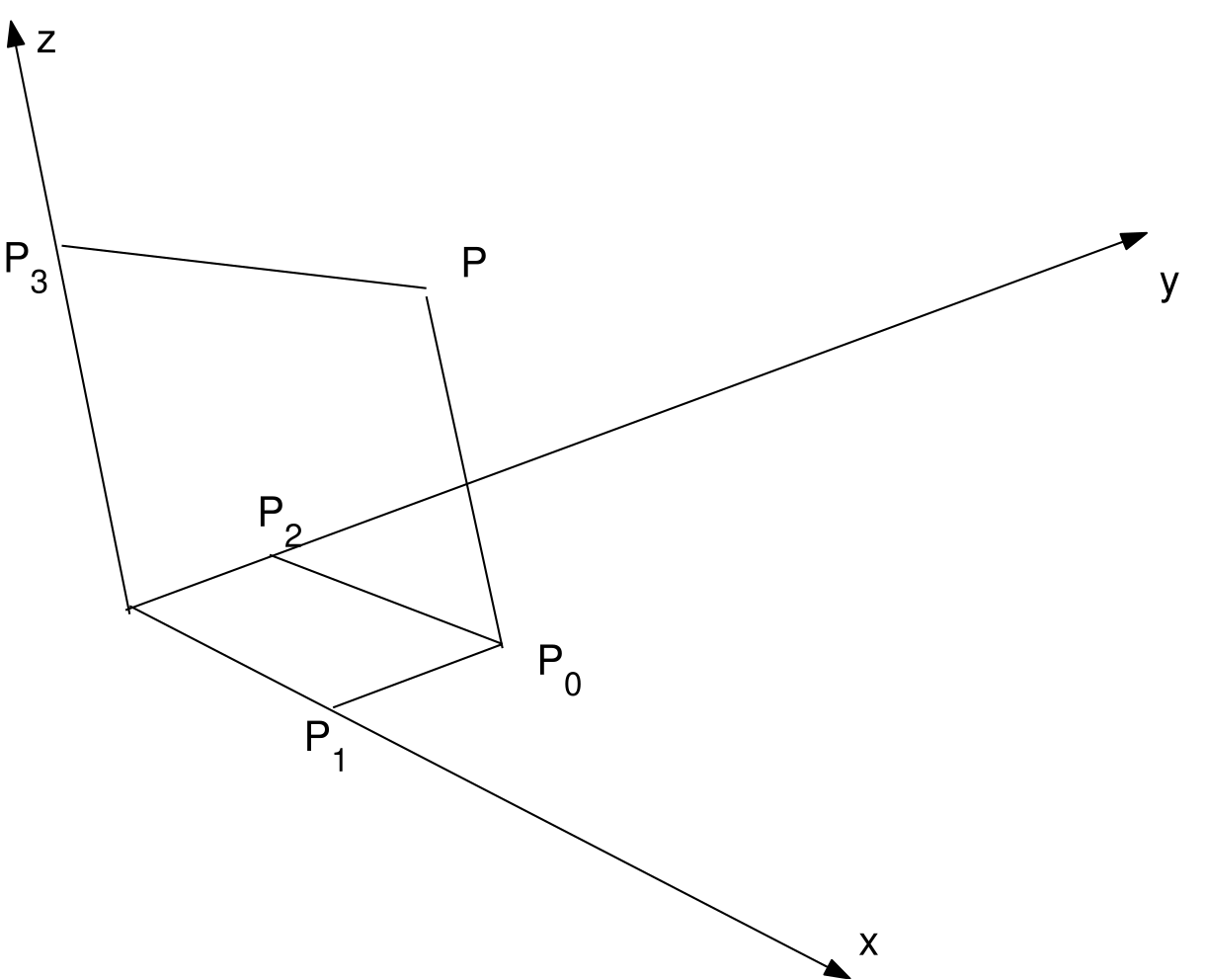
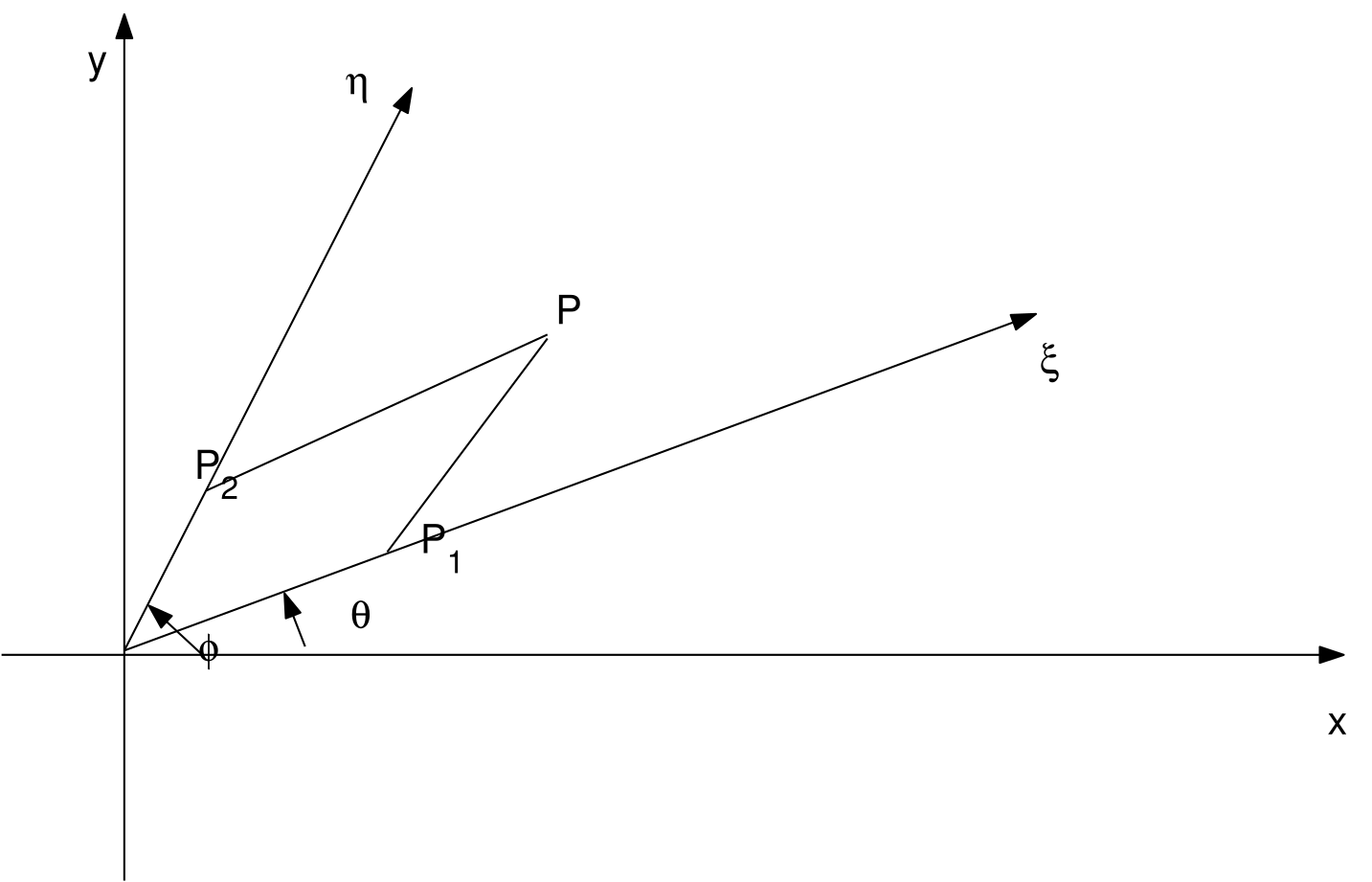
3.6 Coordinate oblique3.7 Trasformazione a coordinate oblique3.8 coordinate
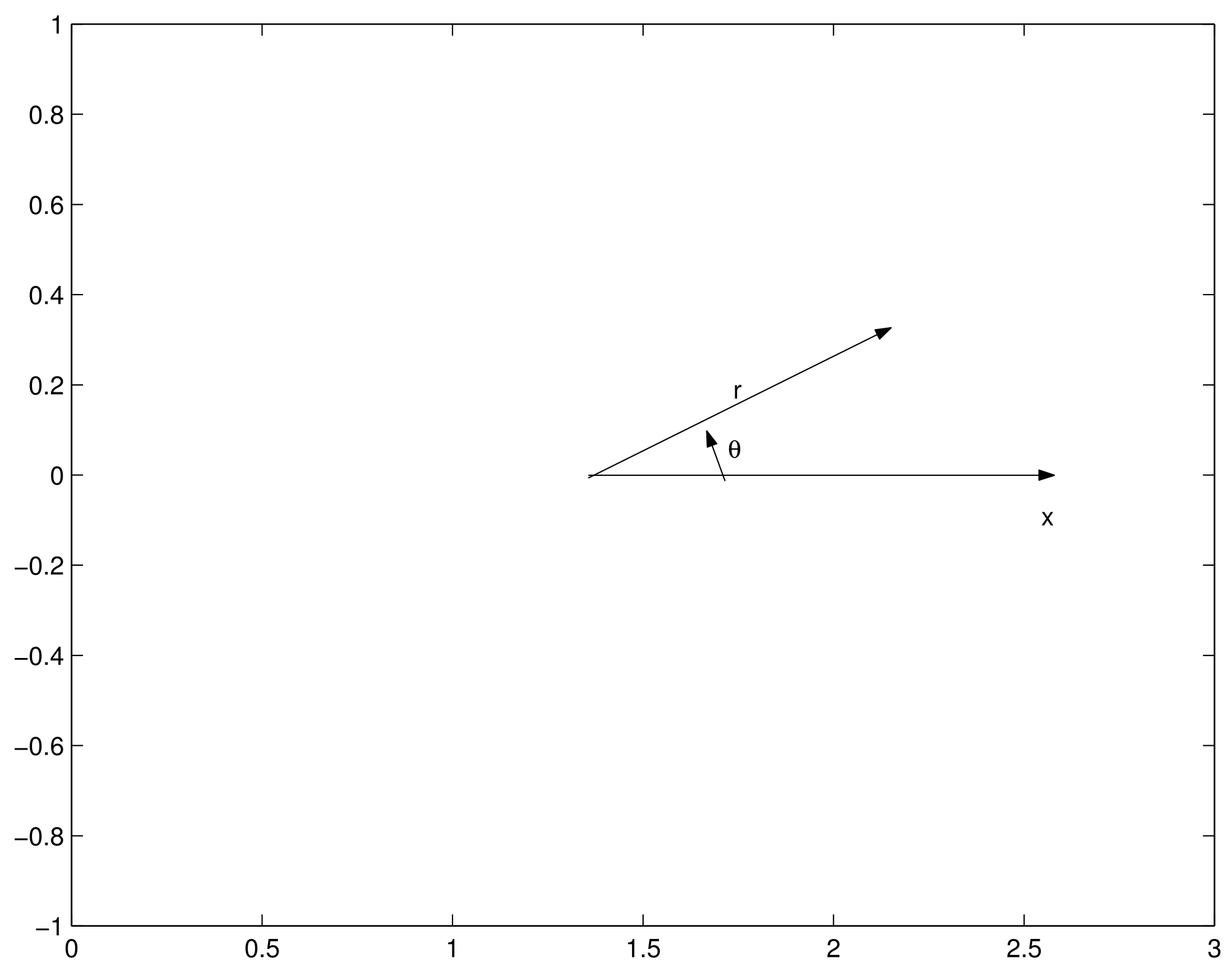
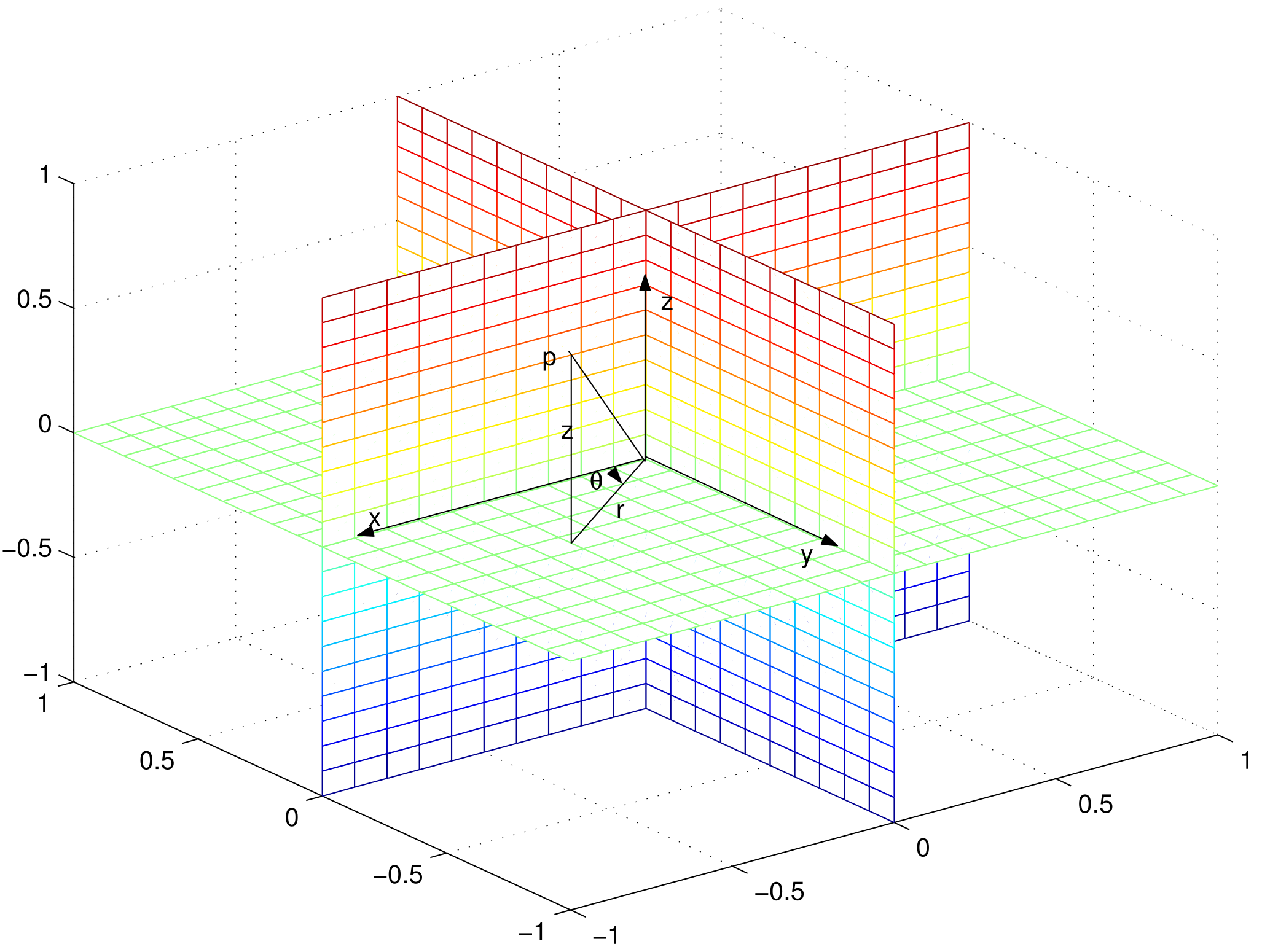
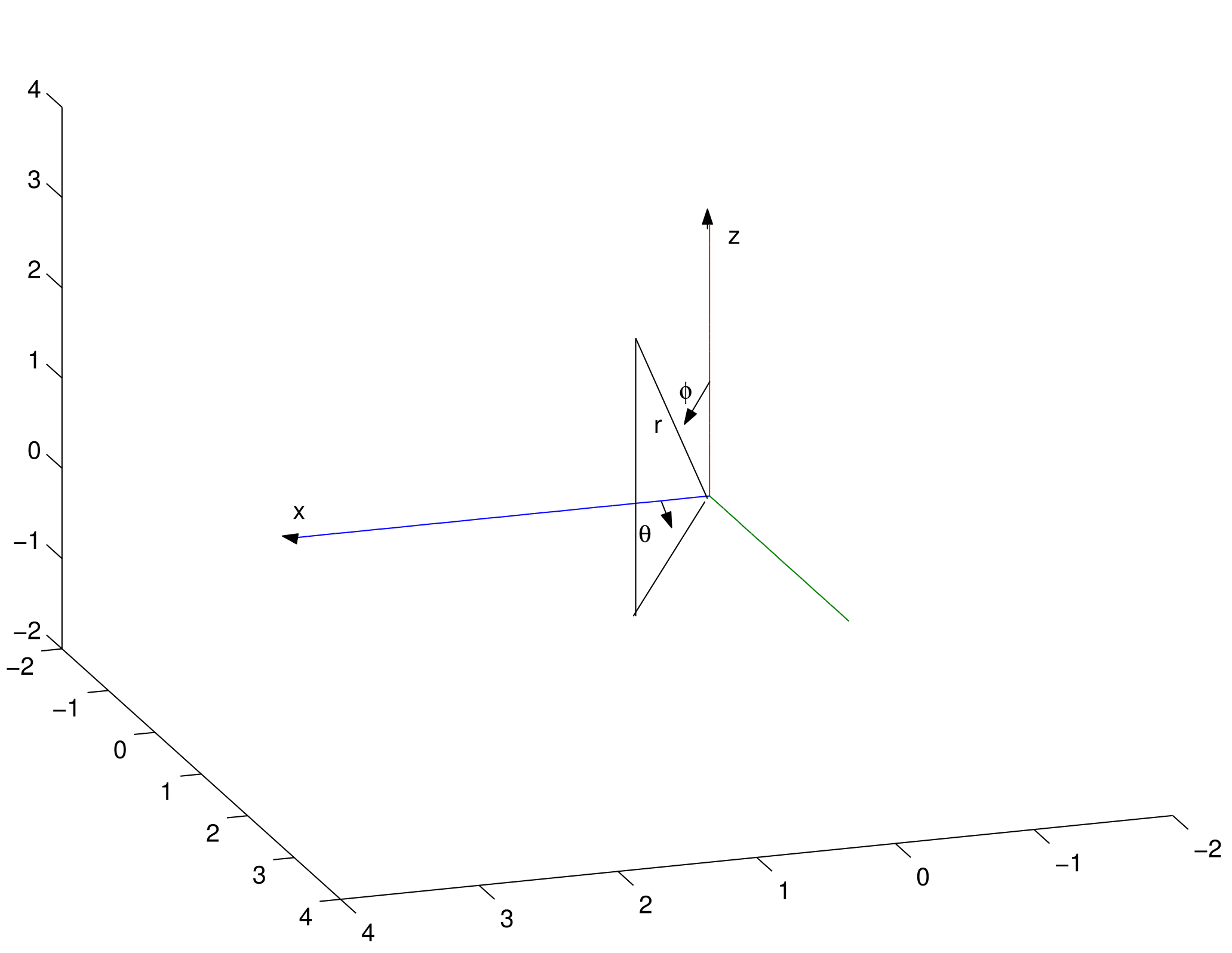
polari3.9 coordinate cilindriche 3.10 coordinate sferiche 4.1 La funzione
dell’esempio 1264.2 Piano tangente e vettore normale4.3 Un punto di
minimo e un punto di sella4.4 Un parallelogramma, la sua immagine e il
parallelogramma che la approssima4.5 un campo vettoriale4.6 Paraboloide
di rotazione4.7 Paraboloide di rotazione e sue curve di livello4.8 La
funzione (4.10)4.9 Una funzione omogenea4.10 Funzione omogenea di grado
4.11 Superficie
di rotazione4.12 Una funzione periodica4.13 La funzione (4.11)4.14 La
funzione (4.12)4.15 Lunghezza d’onda5.1 Esistenza o non esistenza
della funzione implicita5.2 La dimostrazione del teorema della funzione
implicita5.3 Il grafico della funzione 5.4 Esiste
la funzione implicita anche se le condizioni del teorema non sono
soddisfatte5.5 Il grafico della funzione (5.8)5.6 Gradiente nullo ma curva
di livello regolare5.7 Intersezione di due cilindri5.8 Estremi vincolati
e curve di livello5.9 Grafici tangenti e estremi vincolati5.10 6.1 Le
curve (6.1) e (6.3)6.2 La definizione di lunghezza: una curva e i suoi
vettori approssimanti6.3 Versore tangente e versore normale6.4 Le
regioni interna ed esterna e la normale esterna6.5 Regola d’Ampère
per una curva piana6.6 Insieme su cui si proietta una calotta6.7 Una
calotta ed il suo “bordo”6.8 Ancora una calotta col suo “bordo”6.9 Il
piano tangente e la normale ad una superficie6.10 Riferimento mobile
su una curva nello spazio7.1 Domini di integrazione7.2 Suddivisione in
rettangoli di un dominio di integrazione7.3 Riduzione di un integrale
doppio7.4 Riduzione per fili e per strati di un integrale triplo7.5 Volume
di una superficie di rotazione8.1 “Operazioni” sugli archi8.2 Gli
archi (8.8) e (8.9) a sinistra. A destra una regione delimitata da due
archi8.3 Archi che “si elidono”8.4 Integrali di curva di seconda specie ed
archi che “si elidono”8.5 Il flusso8.6 Versi di percorrenza8.7 Formula di
Green8.8 Area di una regione di Jordan8.9 Estensione della formula di
Green8.10 Area di una calotta8.11 Calotta di rotazione (caso particolare:
paraboloide di rotazione)8.12 Flusso attraverso una superficie8.13 Una
sfera e la parte “sotto l’equatore”8.14 Le due regioni8.15 Una sezione
della regione8.16 Ancora la regione8.17 Le due orientazioni del
bordo8.18 Estensione al caso del cilindro8.19 Estensione ad una superficie
non regolare8.20 La costruzione del nastro di Möbius8.21 Il cilindro
e il nastro di Möbius9.1 Un campo vettoriale conservativo ed uno non
conservativo10.1 Spezzata di Eulero 10.2 Nodo e punto di sella 10.3 Centro
e fuoco 10.4 Nella definizione di stabilità in generale si deve scegliere
10.5 Il
caso dell’esempio 277: la limitatezza delle soluzioni non implica la stabilità
10.6 Integrali primi e stabilità 10.7 Il caso considerato nell’esempio 285
Capitolo 1
Serie numeriche
Le serie numeriche vogliono generalizzare la somma di un numero finito di termini
al caso in cui si sommano infiniti termini. Per questo si introduce il limite di una
opportuna successione di “somme parziali”. Prima di tutto quindi ricapitoleremo i
concetti fondamentali relativi alle successioni numeriche.
1.1 Successioni numeriche: ricapitolazione
Una successione numerica è una funzione definita su
ed a valori
in (oppure
in . Noi
qui ci limitiamo a considerare successioni a valori reali). Una successione si indica col
simbolo e si
sottintende che .
Talvolta,
è un qualsiasi numero intero maggiore od uguale ad un certo
che può
anche essere negativo. Se è necessario specificare il primo dei valori dell’indice
scriveremo
. La
successione si chiama:
- “limitata” quando esiste
tale che
per ogni ;
- “convergente”, quando esiste finito il limite ,
che spesso si indica semplicemente come ;
- “divergente” quando
oppure quando ;
- “regolare” quando è convergente oppure divergente;
- “oscillante” quando non è regolare; ossia quando
non esiste, né finito né
né .
Ricordiamo che una successione si dice fondamentale o di Cauchy quando
per ogni
esiste un
tale che
per ogni
e per ogni
si ha:
In simboli:
Vale:
Teorema 1 Ogni successione convergente è fondamentale; ogni successione
fondamentale è limitata e quindi ogni successione convergente è limitata.
Naturalmente, esistono successioni limitate e non convergenti. Per esempio la successione di
termine generale .
Invece:
Teorema 2 Ogni successione fondamentale è convergente.
Dim. Accenniamo ai passi cruciali della dimostrazione, che si trova nei testi di Analisi Matematica 1. Sia
la successione. Prima di tutto
si prova che la successione
ammette s.successioni convergenti. Questo si vede così: dato che una successione fondamentale è limitata,
l’immagine di ,
ossia l’insieme
è limitato. Se è finito, almeno uno dei suoi elementi è immagine di infiniti
e quindi la successione
ha una s.successione
costante e quindi
convergente, di ciamo ad .
Se l’insieme
è infinito, esso ammette almeno un punto di accumulazione
,
per il Teorema di Bolzano-Weierstrass. Si costruisce quindi una s.successione
convergente
ad .
L’ultimo passo della dimostrazione consiste nel mostrare che è la successione
stessa che
converge ad ,
usando la definizione di successione fondamentale. _ Una successione
è crescente
quando implica
; decrescente
quando
implica .
Un altro risultato importante da ricordare è il teorema delle funzioni monotone, la
cui formulazione particolarizzata al caso delle successioni è la seguente:
Teorema 3 Sia
una succesione monotona. Esiste
ossia, ogni successione monotona è regolare.
Infine, ricordiamo che se una successione
è regolare, anche la successione che si ottiene da essa trascurandone un numero finito di termini,
ossia è regolare, ed
ha il medesimo limite.
1.2 Le serie numeriche
Sia
una successione di numeri. Per fissare le idee sia
, ma
in modo analogo si può trattare il caso in cui il primo indice sia per esempio
o comunque sia
diverso da . Si chiama
serie dei numeri una
nuova successione
costruita come segue:
|
| (1.1) |
ossia, detto in modo più conciso:
I numeri si chiamano le
somme parziali della serie.
La nuova successione
si indica anche col simbolo
I numeri
si chiamano i termini della serie e si dice che
è il termine
generale della serie. Nella definizione precedente niente si richiede al comportamento della
successione o della
successione . Se
però la successione
converge allora si dice che la serie converge; se la successione
diverge (a
oppure a
)
allora si dice che la serie diverge (rispettivamente a
oppure a
). Se la
successione
è priva di limite, si dice che la serie è oscillante o indeterminata.
Una serie si dice regolare quando converge oppure diverge. Il carattere
della serie o comportamento della serie è la proprietà di essere
convergente, divergente o oscilante. Ricapitolando, se la successione
converge
ad
oppure diverge, dovremmo indicare questo col simbolo
rispettivamente
uguale a
oppure
oppure .
Più brevemente si scrive
Si dice brevemente che
è la somma della serie. Ovviamente, scambiando l’ordine di un numero finito di
termini di una serie, non si cambia nè il comportamento della serie nè la sua
somma, nel caso che la serie sia convergente (diremo più avanti cosa accade
scambiando tra loro infiniti termini della serie). E’ anche vero che, sopprimento o
aggiungendo un numero finito di termini, oppure cambiando il valore di un numero
finito di termini, la serie rimane convergente, divergente o oscillante; ossia:
Teorema 4 Il carattere di una serie non muta alterandone un numero finito
di termini.
Va detto esplicitamente che se la serie è convergente, la somma della
serie cambia alterandone un numero finito di termini. Se invece è
divergente, la sua somma non cambia.
Inoltre:
Teorema 5 Se
converge allora .
Dim. Si indichi con . L’ipotesi è
che la successione converge e
quindi anche la successione
converge, ed al medesimo limite. Dunque,
Di conseguenza:
Esempio 6 La serie di “termine generale” ,
ossia la serie
non converge. _
Invece:
Esempio 7 La successione
(con
fissato) si chiama progressione geometrica (di ragione ).
La serie
si chiama serie geometrica E’ noto che, se ,
e quindi
Si noti che la serie geometrica per definizione inizia con l’indice .
Se per qualche ragione si deve iniziare con un primo indice diverso, di ciò va
tenuto conto nel calcolo della somma. Per esempio
1.2.1 Serie telescopiche
Sia
una successione e sia
(ovviamente definita per ).
Consideriamo la serie
Una serie ottenuta con questo procedimento si chiama serie telescopica E’ facile
calcolare le somme parziali di una serie telescopica:
e, in generale,
Dunque:
Teorema 8 La serie telescopica costruita sopra converge se e solo se
e in tal caso
diverge se
oppure se .
La serie è oscillante se e solo se la successione
è priva di limite.
Esempi
Vediamo alcuni esempi.
Esempio 9 Consideriamo la serie
Questa serie diverge. Infatti,
Sia ha quindi una serie telescopica e
Esempio 10 Consideriamo la serie
Si vede che questa è una serie telescopica notando che
e inoltre .
Dunque,
Se per qualche ragione si devono sommare i termini con ,
allora
Consideriamo ora la serie
Decomponendo in fratti semplici,
Si tratta quindi di una serie telescopica, la cui somma è . _
Infine:
Esempio 11 Anche la serie seguente è una serie telescopica:
Infatti,
e quindi la serie è uguale a
Dunque, la serie converge e la sua somma è . _
Nonostante gli esempi importanti della serie geometrica e delle serie telescopiche,
calcolare esplicitamente le somme parziali di una serie è pressoché impossibile.
L’unica cosa che si può fare è dare condizioni per la convergenza o divergenza di
serie, e quindi, se già si sa che la serie converge, approssimarne numericamente la
somma.
1.3 Criteri di convergenza
Come si è detto, è ben diffcile calcolare esplicitamente le somme parziali di una
serie. Per questo è necessario conoscere dei criteri che assicurino la convergenza o
meno di una serie, senza calcolarne le somme parziali. Dato che la somma
di una serie è il limite della successione delle somme parziali, dovremo
basarci su criteri per l’esistenza del limite, che non facciano intervenire la
preliminare conoscenza del limite stesso. Essenzialmente, questi criteri si
riducono a due soli: il teorema di Cauchy per le successioni e il teorema
delle funzioni monotone. Esaminiamone le conseguenze per il caso delle
serie.
1.3.1 Il teorema di Cauchy per le serie
Vediamo come si trascrive il Teorema di Cauchy nel caso in cui
è la
successione delle somme parziali della serie
Sia, per fissare le idee,
.
Allora,
Possiamo quindi enunciare il Teorema di Cauchy come segue:
Teorema 12 La serie (1.3) converge se e solo se per ogni
esiste
tale che per ogni coppia di indici ,
con
vale
D’altra parte, notiamo che
e quindi:
Corollario 13 Se la serie
converge, anche la serie
converge.
Dim. Infatti, se
converge, per ogni
esiste tale
che per
si ha
E quindi anche la serie
converge, grazie al Teorema 12. _ Più avanti vedremo una
diversa dimostrazione di questo corollario. Si dice che la serie
converge assolutamente quando è convergente la serie
. Il
corollario precedente quindi può enunciarsi in questo modo:
Teorema 14 Una serie assolutamente convergente è convergente.
Questo risultato è molto importante perché la serie
è una serie a termini positivi. Criteri di convergenza facilmente usabili
esistono appunto per il caso delle serie a termini positivi, come ora andiamo a
vedere.
1.3.2 Monotonia e serie a termini di segno costante
Usando il teorema delle funzioni monotone, è facile vedere che
Teorema 15 Sia
una successione a termini positivi. La serie degli
converge se e solo se esiste
tale che
per ogni .
Dim. Ricordiamo il significato di :
prima si costruisce la successione
e poi si studia il limite .
La successione è
crescente perché, essendo
per ogni ,
Dunque la successione
ammette limite, finito o meno, per il teorema delle funzioni monotone. Il limite è finito se e solo
se la successione
è superiormente limitata, ossia se e solo se esiste
tale che
per ogni
. _ Il
teorema facilmente si estende al caso di successioni a termini negativi oppure
definitivamente positive o negative. Inoltre:
Teorema 16 (Teorema del confronto) siano
e
due serie a termini positivi, con
per ogni .
Allora, se
converge, anche
converge; se
diverge lo stesso fa .
Questo semplice risultato ha come conseguenza due importanti criteri di convergenza
per le serie a termini positivi:
Teorema 17 (Criterio della radice) Sia
per
ogni :
Dim. Da
segue infatti e, se
, la convergenza
della serie
segue dall’esempio 7 e dal Teorema del confronto. Se per un
vale
allora
Di conseguenza il termine generale della serie non tende a zero, e quindi la serie
non converge. _ Si ha inoltre:
Teorema 18 (Criterio del rapporto) Se vale definitivamente
allora
converge; se
allora
diverge.
Dim. Proviamo l’asserto nel caso in cui la (1.4) valga per ogni
. Se
allora
,
e, in
generale, . Si
sa che se
allora
converge, si veda l’esempio 7. L’asserto segue quindi dal Teorema del confronto. In
modo analogo si vede il secondo asserto. _ Ricordando i teoremi sui limiti, si può
enunciare il corollario seguente:
Corollario 19 Sia
una serie a termini positivi. Vale:
- se
allora la serie converge;
- se
allora la serie converge;
- se
allora la serie diverge;
- se
allora la serie diverge.
Concludiamo con un esempio:
Esempio 20 Consideriamo la serie
Mostriamo che questa serie è divergente. Si noti che per ogni
vale
Infatti, la funzione
è concava e quindi ha grafico che sta sotto a ciascuna delle sue tangenti; e
è la
tangente nell’origine. In particolare vale
Abbiamo visto che la serie a termini positivi
diverge, si veda l’esempio 9. Dunque, per confronto, anche la serie (1.5)
diverge. _
La serie (1.5) si chiama serie armonica. Si osservi che il carattere della serie
armonica non può determinarsi usando il criterio del rapporto oppure quello della
radice. Infatti, nel caso della serie armonica,
All’esempio 24 vedremo una serie di termine generale
che
è convergente e tale che anche per essa vale
Combinando questi due esempi si ha:
niente può dedursi dai criteri della
radice e del rapporto, se il numero
che compare in tali criteri è uguale ad
.
Le serie a termini positivi hanno una notevole proprietà, che non è condivisa dalle
generiche serie a termini di segno variabile: se si altera l’ordine di infiniti termini di
una serie si trova una nuova serie, che generalmente ha un comportamento diverso
da quello della serie di partenza. Invece:
Teorema 21 Due serie a termini positivi, con gli stessi elementi in ordine
diverso, hanno la medesima somma.
La formula di Stirling
Per ragioni che vedremo, molto spesso il termine generale di una serie contiene dei
fattoriali. I fattoriali hanno un “buon comportameno” rispetto al rapporto, nel
senso che permettono facilmente di fare semplificazioni. Invece, il criterio della
radice sembra diffcile da usare in presenza dei fattoriali. In realtà non è
così grazie alla formula di Stirling
|
| (1.6) |
La dimostrazione si trova nei testi di Analisi Matematica 1.
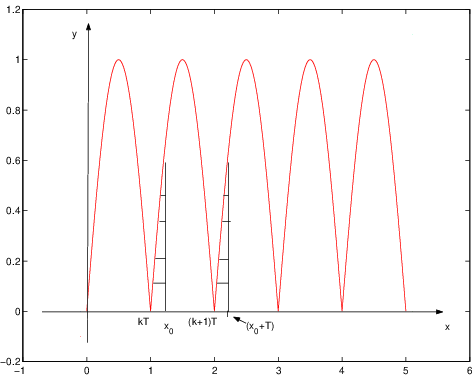
1.3.3 Il test di MacLaurin
Consideriamo le somme parziali di una serie a termini positivi
Esse sono
Queste espressioni si possono interpretare come somma di aree di rettangoli interpretando
come misura
della base ed
come misura dell’altezza.
ove
è la funzione costante a tratti
Dunque, la somma della serie è l’integrale improprio di
:
Pensiamo ora ai rettangoli messi come in figura 1.1, a sinistra, e supponiamo di poter trovare
due funzioni,
e , che
prendono valori maggiori o uguali a zero e tali che inoltre valga
Si veda la figura 1.1, a destra. In tal caso si ha
La serie è a termini positivi e quindi regolare; le funzioni sono non negative e
quindi ammettono integrale improprio finito o meno. Dunque, dal teorema di
confronto per i limiti, si ha
Ricapitolando,
- Se
allora la serie diverge;
- Se
allora la serie converge. In questo caso si trovano anche stime, da sotto
e da sopra, per la somma della serie.
Il caso tipico in cui quest’argomento si applica facilmente è il caso in cui esiste una funzione
definita
su ,
decrescente e inoltre
In questo caso,
|
| (1.7) |
Definiamo, per ,
e notiamo che la (1.7) si scrive
Inoltre,
|
|
Ossia, nel caso descritto, i due integrali impropri hanno il medesimo
comportamento e questo comportamento è ereditato dalla serie. Possiamo quindi
enunciare:
Teorema 22 (Test di MacLaurin) Sia
una funzione non negativa e decrescente definita su .
Si consideri la serie
Le sue somme parziali verificano
|
| (1.8) |
In particolare, la serie a termini positivi
converge se e solo se
L’interesse di questo teorema sta nel fatto che talvolta l’integrale di
può
esplicitamente calcolarsi mediante il calcolo delle primitive; e comunque esistono
test effcienti per lo studio della convergenza o divergenza degli integrali impropri.
Esempio 23 Si sa già che la serie armonica
diverge. La serie
converge, come si vede dal criterio di MacLaurin. Infatti, la funzione
ha integrale improprio convergente:
Procedendo in modo analogo
si provi invece che
Esempio 24 Si calcola immediatamente
Dunque,
converge per ,
diverge altrimenti. _
Possiamo combinare l’esempio 24 col criterio di confronto, ottenendo:
Corollario 25 Consideriamo la serie
.
Vale:
In particolare, possiamo enunciare:
Se
e se
esiste
tale che
allora la serie
converge.
Per ora, stiamo lavorando con serie a termini positivi, ma non abbiamo scritto
esplicitamente questa condizione perché vedremo, al Corollario 27, che il test
precedente vale per ogni serie.
1.3.4 Serie a termini di segno qualsiasi
Sulle serie a termini di segno qualsiasi, limitiamoci ad
osservare due proprietà. Si è già detto che se la serie
converge, si
dice che la serie
converge assolutamente. Ricordiamo, dal teorema 15:
Teorema 26 Una serie assolutamente convergente è convergente.
Ricordiamo ora che quando
è un infinitesimo, e
ciò accade se e solo se
è un infinitesimo. Quindi:
Corollario 27 Se esite
tale che ,
allora la serie
converge assolutamente, ed è quindi convergente.
Infine, si dice che una serie è a segni alterni se ha forma
|
| (1.10) |
ossia se gli addendi si susseguono cambiando segno ad ogni passo. Esiste, per le
serie a segni alterni, una notevole condizione suffciente di convergenza, e anche una
stima per la somma della serie:
Teorema 28 (Criterio di Leibniz) Se valgono ambedue le condizioni
-
- la succesione
è decrescente, ossia
per ogni
allora la serie a segni alterni (1.10) converge; inoltre, detta
la somma della
serie, per ogni
vale:
La dimostrazione della convergenza è nell’Appendice 1.8.2.
Esempio 29 Consideriamo la serie
Questa serie si chiama serie di Mengoli Il criterio di Leibniz mostra che questa
serie converge. La somma della serie è nota:
Il Teorema 28 dà anche una stima dell’errore che si commette sommando
termini: l’errore è minore di . _
1.4 Alcuni esempi numerici
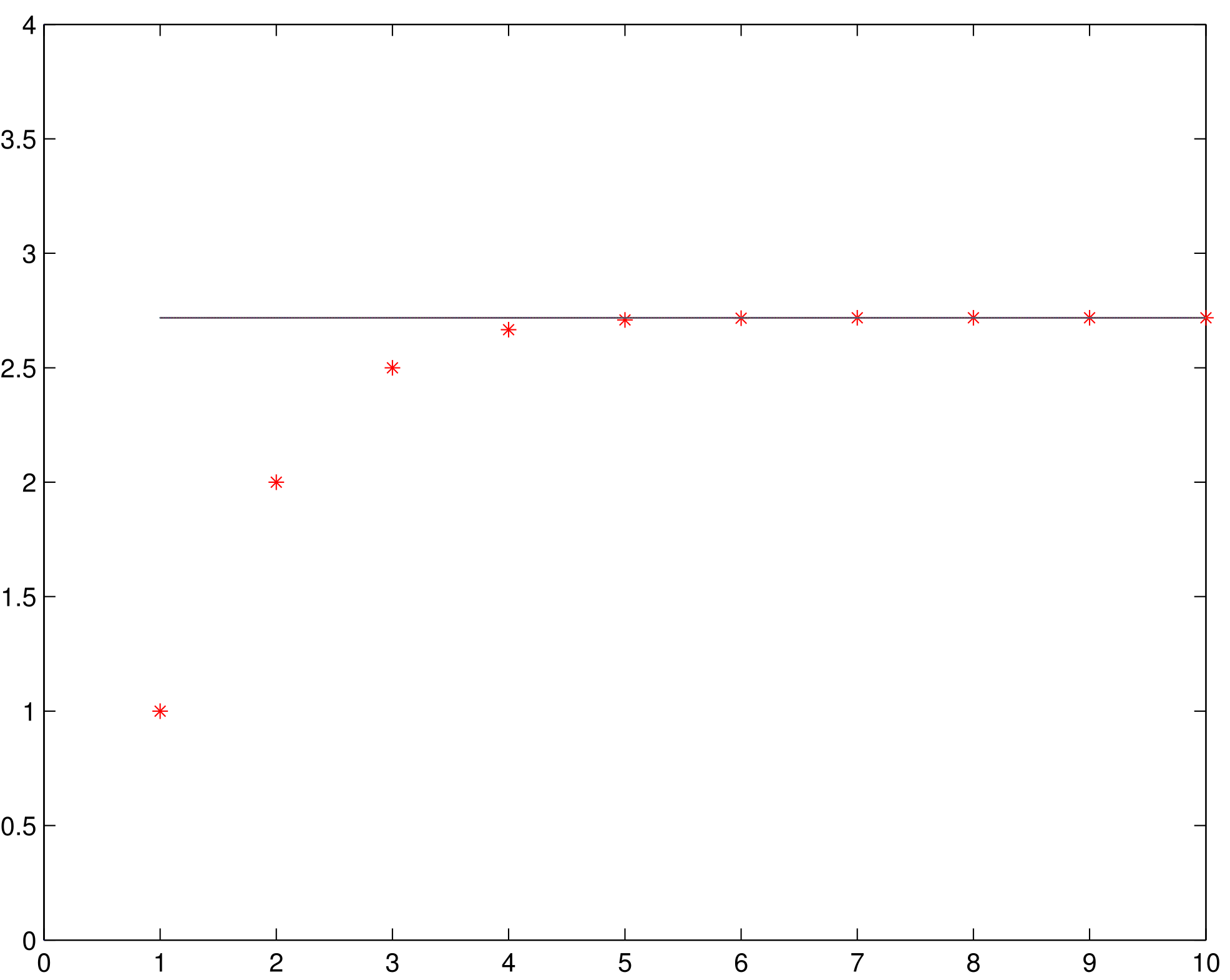
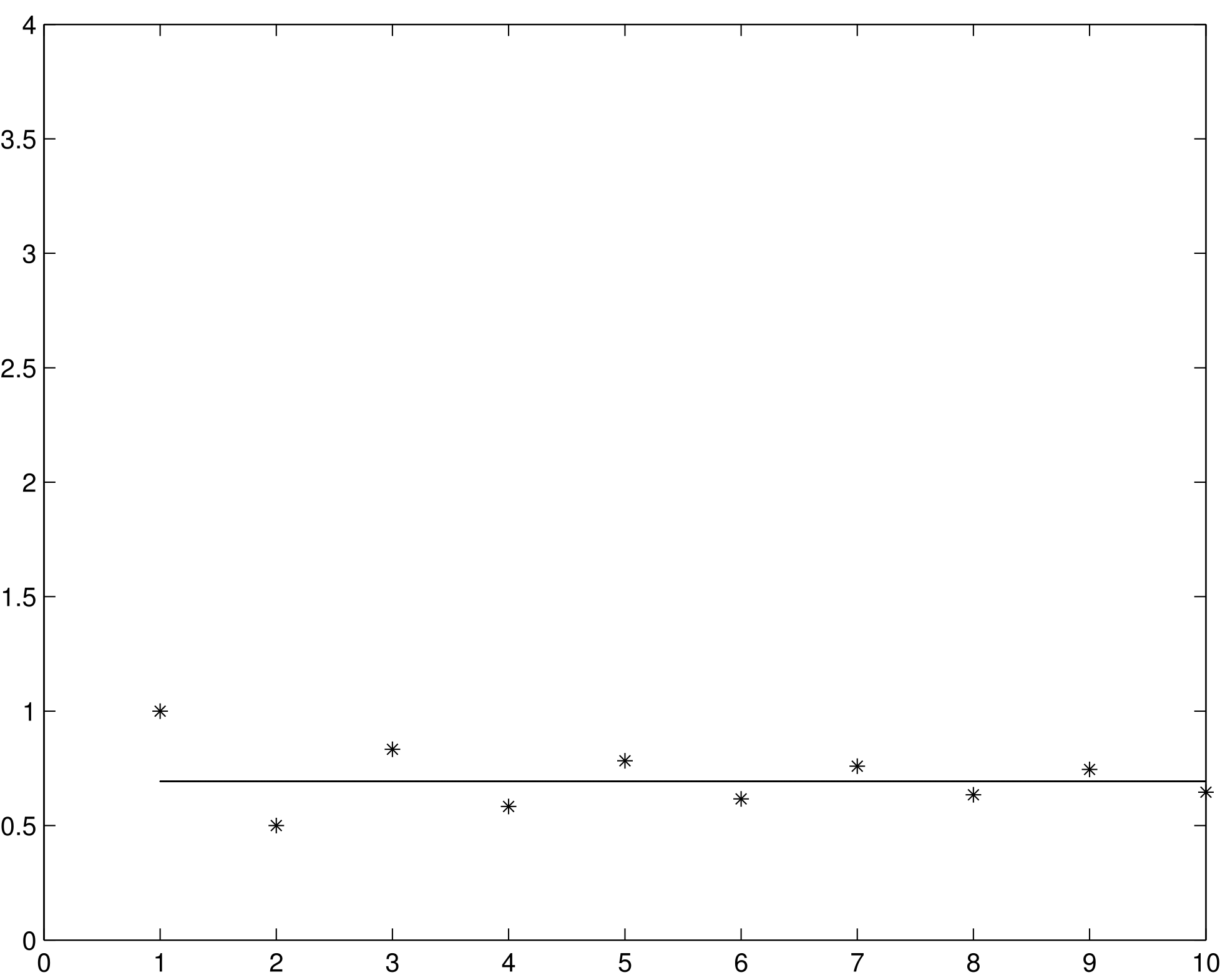
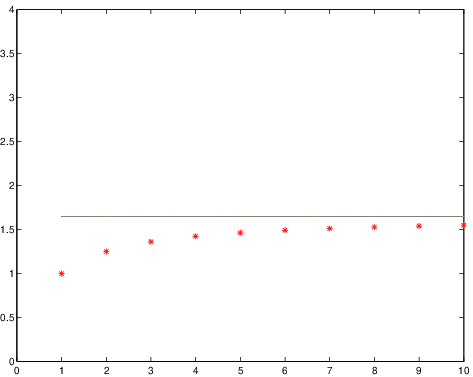
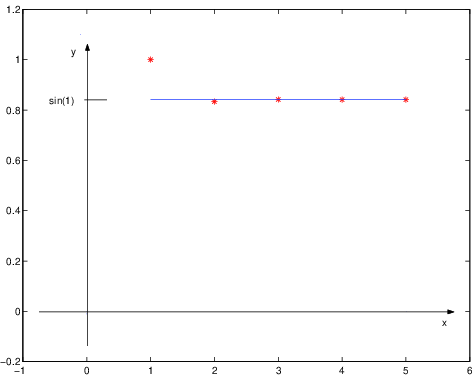
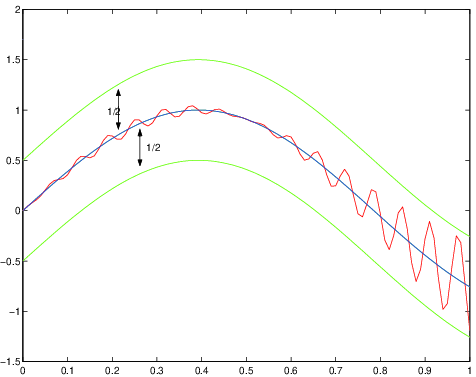
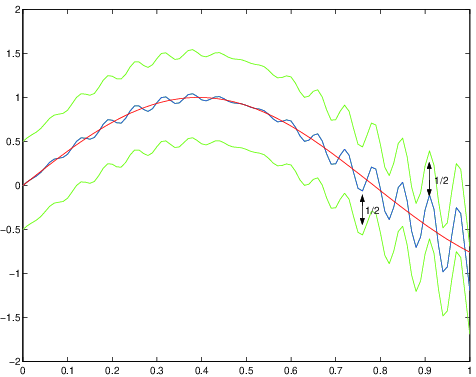
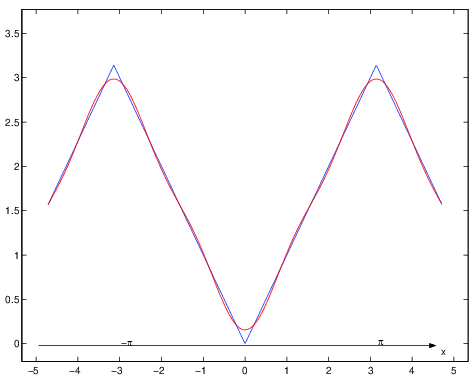
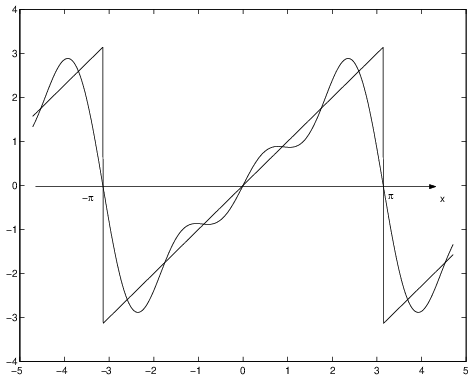
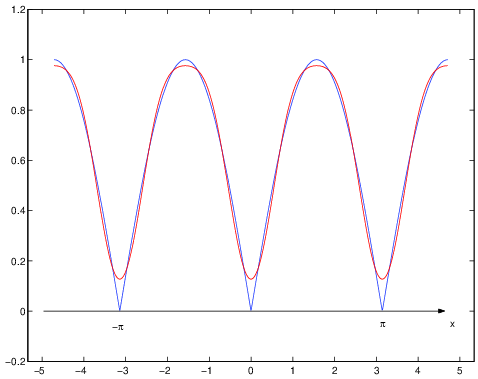
Le figure 1.2, 1.3 e 1.4 mostrano alcuni esempi numerici di somme parziali di
serie convergenti. Le serie sono specificate nelle intestazioni delle figure.
1.5 Convergenza condizionata ed incondizionata
Il concetto di serie generalizza quello di somma finita. In una somma finita il
risultato non dipende dall’ordine degli addendi (proprietà commutativa
dell’addizione). Nel caso delle serie, l’asserto analogo vale se si scambiano tra di loro un
numero finito di termini. E’ FALSO se si scambia il posto di infiniti termini. Mostriamo
un esempio:
Esempio 30 Consideriamo la serie di Mengoli .
Si sa che questa serie converge. Mostriamo che è possibile scambiare il posto di
infiniti termini, in modo da ottenere una serie divergente a .
Ricordiamo per questo che
diverge e quindi anche
diverge. Conviene vedere una dimostrazione di questo fatto, diversa da quella
già vista: consideriamo
(si è usato il fatto che si sommano
termini, ciascuno dei
quali è maggiore di ).
Ciò contrasta col criterio di convergenza di Cauchy, e mostra che la serie diverge.
Dato che il carattere di una serie non dipende dai primi elementi, anche ciascuna
delle serie
è divergente. Ora consideriamo la serie di Mengoli, per semplicità cambiata di segno.
Essa converge a .
Vogliamo riordinarne gli elementi in modo da trovare una serie divergente a
. Per
questo sommiamo prima i termini di indice pari, fino ad un certo indice
tale
che
Questa è la somma parziale
della serie riordinata. Sottraiamo quindi il primo termine di indice dispari, ossia
ottenendo una
somma parziale
tale che
Consideriamo ora la serie (1.11) con .
Come si è detto, questa serie diverge. Dunque, possiamo
sommare ulteriori termini di indice pari alla somma parziale
già ottenuta, fino a trovare una somma parziale maggiore di
;
sottraiamo quindi il primo dei termini di ordine dispari non ancora usati (che è
, minore di
). Si trova una nuova
somma parziale, diciamo ,
maggiore di :
Continuiamo a sommare termini di indice pari (e quindi positivi) fino ad avere una somma parziale
maggiore di
e quindi sottraiamo il primo termine di indice dispari non usato (che è certamente minore
di , infatti è
). Si trova una
somma parziale
tale che
Procedendo in questo modo si trova un riordinamento che conduce ad una serie
divergente a . _
Si potrebbe mostrare che per ogni scelta di
è
possibile riordinare la serie di Mengoli in modo tale da trovare una serie convergente ad
, inclusi
ed
,
o anche in modo da trovare una serie oscillante. Diciamo che una
serie converge incondizionatamente quando una serie converge ad
e inoltre
quando qualunque serie ottenuta riordinandone gli elementi converge al medesimo
numero .
La convergenza incondizionata si caratterizza come segue:
Teorema 31 (Teorema di Dirichlet) Una serie converge incondizionatamente
se e solo se converge assolutamente. Se ciò non accade è possibile riordinare
gli elementi della serie in modo da cambiare il carattere della serie, e anche in
modo da ottenere una serie convergente ad un qualsiasi numero assegnato, o
divergente a
oppure a .
In particolare:
Corollario 32 Ogni serie a termini di segno costante converge
incondizionatamente.
1.5.1 Serie dipendenti da un parametro e serie di funzioni
Torniamo a considerare la serie geometrica,
Questa serie dipende dal parametro
e, come si è visto, converge se ,
diverge se ed oscilla
se . Facendo variare
il parametro ,
ciascuno degli addendi viene ad essere una funzione di
,
Dunque, la serie geometrica può intendersi come serie di funzioni. In generale, data la
successione
i cui elementi sono funzioni (tutte con lo stesso dominio) si chiama serie di funzioni
la serie
La somma della serie si calcola punto per punto; ossia, per ogni fissato valore di
si calcola la somma della
serie di numeri . Il dominio
comune alle funzioni
è ,
ma abbiamo notato che la serie geometrica converge (ad
) soltanto
per .
Dunque, in generale, il dominio su cui è definita la somma di una serie di funzioni
è più piccolo del dominio comune delle funzioni. Le serie di funzioni si studieranno
al Capitolo 2. Va tenuta presente la loro definizione per capire alcune sottigliezze
del paragrafo 1.6.
1.6 Operazioni algebriche e serie
Il concetto di “serie” estende quello di “somma finita”. Le somme finite godono di
utili proprietà, come per esempio la proprietà distributiva del prodotto sulla
somma, la proprietà associativa e “dissociativa”. Ci possiamo chiedere se le
analoghe proprietà valgono per le serie. Per questo dobbiamo tener conto di due
problemi:
- la “somma di somme finite” non dipende dall’ordine degli addendi:
Si sa già che la somma della serie varia cambiando l’ordine dei suoi
termini. Quindi dovremo aspettarci che una proprietà analoga non valga
necessariamente per le serie.
- la somma di serie è definita tramite il concetto di limite; le relazioni tra
limiti ed operazioni sono dissimmetriche. Di ciò dobbiamo tener conto per
enunciare i risultati relativi alle serie.
Queste osservazioni suggeriscono di elencare prima le relazioni tra limiti ed operazioni
sia nella versione “giusta” che nella versione “sbagliata”:
Ricordiamo brevemente perché le affermazioni a destra sono sbagliate: per esempio
nel caso 1, il limite della somma di due funzioni può esistere, senza che le due
funzioni individualmente abbiano limite, come è il caso del limite, per
,
quando le due funzioni sono
In questo caso,
Questo limite non è uguale a
per la semplice ragione che i due limiti non esistono. Il caso 2, del prodotto è
analogo. Vale la pena però di vedre un caso banale che però può inndurre in
errore nel caso delle serie: NON è vero che la formula seguente vale per OGNI numero
reale :
Questa formula vale solo se
oppure se
esiste finito, come mostrano gli esempi delle funzioni
In ambedue i casi, se ,
mentre le espressioni
non hanno senso. Vediamo ora il caso 3a. Chiaramente, da
non si può dedurre la
convergenza a zero di :
si consideri il caso
ed .
Il caso 3b: si consideri l’esempio della successione
con
, convergente
ad , mentre
. La
successione
è oscillante. Richiamato ció, definiamo:
Somma di serie
Prodotto di una serie per un numero
In queste definizioni, l’ordine degli addendi è quello indicato. Supponiamo
Allora:
-
- 1) somma di serie. Vale
purché uno almeno dei due limiti sia un numero oppure sia
che
siano ambedue
oppure .
-
- 2) prodotto di un numero per una serie. La definizione ha senso (e
l’uguaglianza vale) solo se
oppure se la serie converge.
La definizione di prodotto di serie è più complessa e si vedrà nel paragrafo 1.7. Si
potrebbe anche provare:
Teorema 33 Sia
e sia
per ogni .
Sia
una successione limitata. Allora, la serie
converge.
Gli esempi seguenti mostrano i problemi che si possono incontrare usando le operazioni
sulle serie senza le dovute cautele:
Esempio 34 Consideriamo la serie seguente:
Ovviamente la somma della serie è .
Scrivendo
si potrebbe essere tentati di usare una specie di “regola dello scomponendo”
e scrivere
Ovviamente questo non ha senso, perché le due serie a destra non convergono;
e quindi non definiscono numeri che si possano sommare. Un esempio analogo,
un po’ più riposto, è quello delle serie
Le due serie non convergono mentre la serie
converge. _
La regula del prodotto sembra “più innocua” nel senso che sembra più diffcile
sbagliare. In realtà anche questa regola è fonte di errori, come mostra l’esempio
seguente:
Esempio 35 Sia
un parametro reale. Studiare la convergenza della serie
|
| (1.12) |
Si lascia per esercizio di provare che la serie converge per ogni
. Si noti che essa
certamente converge per
perché in tal caso tutti i termini della serie sono nulli. Però, sembra del tutto naturale mettere
in evidenza
portandolo fuori dal segno di serie, scrivendo
e magari studiando la convergenza della serie “piú semplice”
Si dimentica in questo modo che il parametro
può essere nullo. Se
questa serie converge e il procedimento seguito, di mettere in evidenza ,
è corretto. Se però ,
l’ultima serie scritta non converge, mentre la (1.12) ovviamente converge.
L’errore è consistito nel “mettere in evidenza” il fattore
dai termini della serie, errore favorito dal fatto che il fattore è stato indicato
col generico simbolo .
_
Ci sono anche altri errori nei quali si può cadere trattando le operazioni sulle serie
senza la dovuta attenzione:
Esempio 36 Un modo veloce di “calcolare” la somma della serie geometrica
è il seguente:
Dunque,
Questo risultato, apparentemente giusto, è in realtà sbagliato. Infatti da
nessuna parte si è usata la condizione
e quindi sembrerebbe da questo calcolo che la serie geometrica converga per
ogni valore di ,
cosa notoriamente falsa. Si lascia per esercizio di trovare l’errore in questo
ragionamento. _
Infine, vediamo una diversa dimostrazione del Teorema 26 basata sulle proprietà illustrate in questo paragrafo:
La serie
è una serie a termini positivi. Se essa converge, dal teorema 15 convergono anche le due serie
e
,
con
Quindi, per il teorema 16, converge anche
che è .
1.7 Prodotto alla Cauchy
Il prodotto di serie può definirsi in vari modi. Quello più utile è il prodotto alla
Cauchy L’espressione del prodotto alla Cauchy può sembrare macchinosa,
ma se ne capisce la ragione se si considera l’esempio di un prodotto di
polinomi. Consideriamo il caso del prodotto di due polinomi di grado
. Il
prodotto
è la somma di tutti i possibili addendi
con
,
.
Raccogliendo i coeffcienti degli addendi del medesimo grado il prodotto si scrive
come
|
|
Posto ,
il prodotto
si trova scritto come segue:
|
|
Ciò suggerisce le due definizioni seguenti:
- Si chiama convoluzione delle due successioni
e
la successione
con
- Si chiama prodotto alla Cauchy delle due serie
|
| (1.13) |
la serie
Osservazione 37 Se l’indice di una, o ambedue, le serie non parte da zero,
la formula del prodotto alla Cauchy si intende scritta aggiungendo un numero
finito di termini tutti nulli, in modo da far partire gli indici da . _
La convergenza di ambedue le serie (1.13) non implica la convergenza del loro prodotto
alla Cauchy. Vale invece:
Teorema 38 Le due serie (1.13) convergano, ed abbiano somma rispettivamente
e
.
Allora:
- se le due serie convergono ambedue assolutamente, anche il loro prodotto
alla Cauchy converge assolutamente ad .
- se una delle due serie converge e l’altra converge assolutamente, il prodotto
alla Cauchy converge ad ,
in generale non assolutamente.
Concludiamo con un esempio che mostra due serie convergenti (non
assolutamente), il cui prodotto alla Cauchy non converge.
Esempio 39 Consideriamo la serie (convergente per il criterio di Leibniz)
e calcoliamone il prodotto alla Cauchy con se stessa. Notiamo che l’indice di
questa serie parte da
invece che da zero e quindi la formula del prodotto alla Cauchy va lievemente
modificata come detto nell’sservazione 37:
Si vede facilmente che la funzione
è crescente per
e decrescente per
e quindi ha minimo per
e per .
Il minimo vale .
Dunque
il termine generale del prodotto alla Cauchy non converge a zero e quindi la
serie ottenuta come prodotto alla Cauchy non converge. _
1.8 Appendici
1.8.1 Appendice: ancora sul test di MacLaurin
Il test di MacLaurin può ulteriormente precisarsi notando che la (1.8),
ossia
si può anche scrivere come
e che, al crescere di ,
la successione
decresce. e quindi ammette limite compreso tra
ed
.
Infatti, si ha:
|
|
Ossia, al crescere di ,
i valori delle somme parziali e dell’integrale “si avvicinano” anche se l’integrale
improprio (e quindi anche la serie) diverge. Quest’osservazione può usarsi per
ottenere “stime asintotiche” delle somme parziali della serie per grandi valori di
.
Mostriamo questo considerando l’esempio della serie armonica. Sia
La serie armonica è
e quindi diverge, dal criterio di MacLaurin. E’ questo un modo di vedere che la
serie armonica diverge, diverso da quello visto all’esempio 1.5. Però, il criterio di
MacLaurin dà un’informazione in più:
ossia
E inoltre,
esiste, . Il
numero
così definito si chiama costante d’Eulero
1.8.2 La dimostrazione del Teorema di Leibniz
La dimostrazione di questo teorema, e di teoremi più generali di Abel e di Dirichlet
che ora vedremo, è interessante perché permette di introdurre il concetto di
sommazione per parti, da confrontare con quello di integrazione per parti. Nonostante
che il carattere di una serie non dipenda dai primi addendi, in quest’appendice è
bene specificare con cura i valori degli indici. Quindi scriveremo per esempio
per intendere che il valore del primo indice della successione è
. Inoltre, se
indica una
successione, con
intendiamo la successione delle sue somme parziali:
Sia una successione.
Con intendiamo
la successione .
Sia .
La formula di sommazione per parti è:
Questa formula si dimostra facilmente scrivendo la somma per esteso:
|
|
Ci serve inoltre un risultato preliminare:
Lemma 40 Sia
una serie tale che la successione
delle somme parziali sia limitata e sia
una successione positiva decrescente. Allora, la serie
converge assolutamente.
Dim. Si noti che la successione
è convergente, ,
per il teorema della funzione monotona, e quindi limitata. Anzi,
Inoltre, .
L’asserto del lemma segue perché ora proviamo che
.
Infatti,
Osservazione 41 Si noti che il Lemma 40 non richiede la convergenza della
serie . _
Consideriamo ora la serie
e notiamo che
Introducendo i numeri
definiti da
e usando la regola di sommazione per parti con primo indice
, le
sue somme parziali si rappresentano come segue:
|
|
Dunque, per garantire la convergenza della serie
,
basta dare condizioni che garantiscano l’esistenza dei due limiti
|
| (1.15) |
Un criterio per questo è dato dal Teorema di Dirichlet, che immediatamente
implica il criterio di Leibniz:
Teorema 42 (Teorema di Dirichlet) Sia
una successione a valori positivi, decrescente e convergente a zero. Sia
una serie tale che
rimane limitata. Allora, la serie
converge.
Dim. Infatti, il limite (1.14) è nullo perché
è limitata e
. Il limite (1.15)
esiste per il Lemma 40. _ Dimostrazione del criterio di convergenza di Leibniz.
La dimostrazione del criterio di Leibniz per la serie a segni alterni
con
decrescente e convergente a zero, segue immediatamente: basta definire
e
e
notare che
e quindi
rimane limitata. Una diversa condizione per l’esistenza dei due limiti (1.14)
e (1.15) è data dal teorema seguente:
Teorema 43 (Teorema di Abel) Sia
una successione a valori positivi e decrescente. Sia
una serie convergente. Allora, la serie
converge.
Dim. Per ipotesi, esistono ambedue i limiti
e
. Dunque, esiste il
limite (1.14). La successione ,
essendo convergente è anche limitata e quindi il limite (1.15) esiste per il
Lemma 40. _
Capitolo 2
Successioni e serie di funzioni
In questo capitolo studiamo le successioni e le serie di funzioni.
Studiamo quindi particolari metodi per approssimare una data funzione
mediante serie i cui termini sono funzioni elementari: monomi o funzioni
trigonometriche.
2.1 Introduzione
Ricordiamo, dal Par. 1.5.1, che una successione di funzioni è una trasformazione che ad ogni numero
naturale associa una
funzione definita
su un dominio ,
lo stesso per ogni .
Stando così le cose, il problema della convergenza della successione di funzioni si studia per
ogni fissato ;
ossia si studia una successione numerica per ogni valore del parametro
. Se la succesisone
converge a
per ogni
, si dice che la
successione converge
puntualmente ad
su . In
realtà questo è un modo piuttosto semplicistico di procedere. Le
applicazioni richiedono infatti di studiare la convergenza rispetto ad
opportuni concetti di “distanza” tra funzioni. Ciò è quanto facciamo
in questo capitolo. Notazione. Da ora in poi di regola useremo una
notazione meno “elementare”: per indicare una funzione invece di scrivere
scriveremo semplicemente
. Invece, col simbolo
intenderemo il
valore che la funzione
assume nel punto .
In certi casi questo può condurre ad ambiguità ed allora useremo notazioni del tipo
per indicare la
funzione che ad
associa . Va detto
che la notazione
non si può usare per specifiche funzioni: la funzione
si indicherà
semplicemente con .
Dunque, successioni e serie di funzioni di regola si indicheranno con la
notazione
ecc. Invece scriveremo esplicitamente
quando dovremo considerare successioni o serie di funzioni particolari, per
esempio
2.2 Distanze tra funzioni
Noi considereremo funzioni definite su un fissato insieme
che
sarà sempre un intervallo. Specificheremo volta per volta se tale intervallo deve essere
limitato e/o chiuso. Inoltre, non considereremo tutte le possibili funzioni definite su
, ma
le funzioni di una delle tre classi seguenti:
- col simbolo
si intende l’insieme delle funzioni continue su .
Implicitamente usando questo simbolo si intende che
sia limitato e chiuso, .
- col simbolo
si intende l’insieme delle funzioni il cui valore assoluto è integrabile su
:
L’insieme
è ora un intervallo qualsiasi.
- col simbolo ,
si intende l’insieme delle funzioni tali che
L’insieme
è ora un intervallo qualsiasi. Si noti la presenza del segno
e del quadrato. Ovviamente, se la funzione prende valori reali, .
Però molto spesso la funzione
prende valori complessi e in tal caso il segno di modulo è necessario.
Osservazione 44 L’integrale che usiamo è l’integrale di Riemann. Si
ricordi che una funzione integrabile secondo Riemann è necessariamente
limitata. Usando questa proprietà, si potrebbe mostrare che, se l’intervallo
è limitato, i due insiemi
ed
hanno i medesimi elementi. I due insiemi invece sono diversi se
è illimitato o se si usano concetti diversi di integrale, che permettono di
integrare anche funzioni illimitate. A noi interessa sapere che:
I tre insiemi sopra definiti sono spazi lineari, nel senso visto nei corsi di geometria,
rispetto alle operazioni
In questi spazi lineari si introduce una distanza come segue:
- in
si pone
(si noti che il massimo esiste, dal teorema di Weierstrass, perché
l’intervallo
è limitato e chiuso.) La distanza sopra definita si indica anche col simbolo
- Le distanze in
e in
si indicano anche, rispettivamente, con i simboli
e sono definite da
Si noti che in questi simboli l’intervallo
è sottinteso e che spesso si scrive, rispettivamente,
usando il simbolo di “norma della differenza”, al posto di quello di distanza
Osservazione 45 Non ci serve essere precisi su questo. Però va detto che
solamente la norma
è effettivamente una norma e che solo
è effettivamente una distanza. Infatti, se ,
se
per ogni
e se
per
mentre ,
allora ,
nonostante che
e
siano tra loro diverse. _
Accade che
quando il grafico di
sta in un “tubo” di ampiezza
intorno a quello di ,
come in figura 2.1. Si noti che il “tubo” può essere disegnato intorno ad una
qualsiasi delle due funzioni. Ciò fatto si richiederà che il grafico dell’altra
stia in tale “tubo”.
Invece, quando
accade che è minore di
l’area del trapezoide di ,
ossia l’area della superficie compresa tra i grafici delle due
funzioni. La figura 2.2, a sinistra, riporta il grafico di
ed a destra quello
di (per le medesime
due funzioni
e )
con tratteggiata la regione la cui area deve essere “piccola”
se si vuole che queste “distino di poco” rispettivamente in
ed in
. La figura suggerisce che
la distanza, nel senso ,
o , tra due
funzioni possa essere “piccola” anche se i due grafici diventano “molto distanti” per certi
valori di .
Scriviamo ora esplicitamente la definizione di convergenza rispetto alla distanza
.
Questo tipo di convergenza si chiama convergenza uniforme
La successione di funzioni
converge uniformemente ad
su
se per ogni
esiste
tale che
per ogni
vale
ossia, per
vale
Per contrasto, diamo la definizione di convergenza puntuale: la successione
converge
puntualmente ad
su quando per
ogni e per ogni
esiste un numero
tale che se
si ha, per questo
particolare numero ,
. Cambiando il
punto cambia
anche il numero .
Si ha convergenza uniforme quando si può trovare un numero
che va bene per ogni
. Diamo ora la definizione
di convergenza in
ed in .
La successione
converge ad
in
se per ogni
esiste
tale che
per ogni
si ha
La successione
converge ad
in
se per ogni
esiste
tale che
per ogni
si ha
La convergenza in
si chiama anche convergenza in media e la convergenza in
si chiama
anche convergenza in media quadratica mentre, come si è già detto, la convergenza
in si
chiama convergenza uniforme.
Osservazione 46 Supponiamo che la successione di funzioni
sia definita su un dominio ,
.
Se la successione converge uniformemente su ,
essa converge uniformemente sia su
che su
e, viceversa, se la successione converge uniformemente su
e anche su ,
essa converge uniformemente anche su .
Asserto analogo vale anche per la convergenze in media e per la convergenze
in media quadratica. _
Vediamo ora due figure che illustrano il significato della convergenza uniforme e
della convergenza in media. La fig. 2.3 a sinistra suggerisce la convergenza
uniforme. La figura a destra vuol suggerire la convergenza in media, e
vuol sottolineare che la convergenza in media non implica la convergenza
puntuale. I grafici rappresentati a destra sono quelli delle funzioni
con ,
,
,
.
Si provi dettagliatamente, facendo uso della definizione, che la successione
,
,
converge a zero in media ed in media quadratica, ma non uniformemente.
Infine, enunciamo il lemma seguente, immediata conseguenza del teorema di
confronto per i limiti. La dimostrazione è lasciata per esercizio.
Lemma 47 Sia
una successione di funzioni su un intervallo .
Su tale intervallo sia anche definita una funzione .
Sia
una successione numerica tale che
- se vale
allora la successione
converge uniformemente a .
- se vale
allora la successione
converge a
in .
- se vale
allora la successione
converge a
in .
2.2.1 Il prodotto interno su
Su si
può definire un prodotto interno o prodotto integrale come segue: siano
e
due funzioni a quadrato integrabile. Si può provare che il loro prodotto
è integrabile. Definiamo allora il prodotto interno delle due funzioni
e
ponendo
Si noti che se le funzioni prendono valori reali allora il segno di coniugio non ha
alcun effetto; se però esse prendono valori complessi il coniugio è importante
perché è grazie ad esso che si ottiene
Quest’uguaglianza giustifica il termine “prodotto interno”
(o “prodotto scalare”): nel caso dei “vettori ordinari” di
si ha
infatti
Diciamo che due funzioni
e sono
ortogonali in
quando
Naturalmente, per dire che
è ortogonale a ,
scriveremo
Una proprietà importante del prodotto interno in
è
che per esso vale il teorema di Pitagora:
Teorema 48 Se
allora .
Dim. Infatti si ha
In particolare,
Osservazione 49 Va notato esplicitamente che non esiste nessun concetto
analogo a quello di prodotto interno per le distanze in
o di . _
2.2.2 Proprietà della convergenza uniforme
La sola convergenza puntuale è troppo debole per avere proprietà importanti di
qualche tipo. Infatti:
- esistono successioni di funzioni integrabili che convergono puntualmente
a funzioni non integrabili.
Per vedere un esempio, ricordiamo che i numeri razionali sono
numerabili, ossia sono immagine di una successione iniettiva. Sia
questa successione e definiamo la funzione
Ciascuna delle funzioni
è integrabile, con integrale uguale a zero, perché
è zero salvo che in un numero finito di punti. La successione
converge alla funzione
di Dirichlet, che vale
sui razionali e vale
sugli irrazionali. Questa funzione non è integrabile.
- esistono successioni di funzioni continue che convergono puntualmente a
funzioni discontinue.
Un esempio è il seguente: sia
e sia .
Ciascuna funzione è continua, ma la successione di funzioni
converge
puntualmente su
alla funzione
Questa funzione è discontinua. E’ per questa ragione che vanno introdotti
concetti più restrittivi di convergenza. In questo paragrafo presentiamo le relazioni
tra il concetto di convergenza uniforme e le proprietà di limite, derivabilità ed
integrazione.
Il teorema centrale è il seguente:
Teorema 50 Sia
una successione di funzioni, definite su un intervallo ,
ciascuna delle quali è continua in un punto .
Se la successione converge ad una funzione
uniformemente su
allora anche la funzione
è continua in .
Omettiamo la dimostrazione. Ricordando che le funzioni continue su un intervallo
limitato e chiuso sono integrabili si ha:
Corollario 51 Sia
una successione di funzioni continue su un intervallo limitato e chiuso .
La successione converga uniformemente su
ad una funzione .
Allora, la funzione
è continua e quindi anche integrabile su .
Sotto le ipotesi del corollario precedente, può dirsi di più: l’integrale di
è il limite degli
integrali delle .
Ossia:
Teorema 52 Sia
una successione di funzioni continue su un intervallo limitato e chiuso
. La successione converga
uniformemente su
ad una funzione .
Allora,
|
| (2.1) |
Dim. Ricordando la definizione di limite, dobbiamo provare che per ogni
esiste
tale che
per ogni
si ha
Dalla linearità e dalla proprietà di monotonia degli integrali,
e quindi basta provare che
per
suffcientemente grande. Ricordiamo che la successione
converge ad
uniformemente
su : scelto un
qualunque
esiste tale
che, per ogni
si ha
e quindi anche
con la lunghezza
di . L’asserto
segue scegliendo
e . _
Osservazione 53 Ricordiamo, dall’Osservazione 46, che se
e se la successione
converge uniformemente su ,
essa converge uniformemente sia su
che su .
D’altra parte, l’integrale su
è la somma dei due integrali su
e su .
Quindi il teorema si applica facilmente anche a successioni uniformemente
convergenti di funzioni continue a tratti e questo è suffciente per molte
applicazioni. Si potrebbe però provare che la semplice integrabilità di ciascuna
delle funzioni
e la convergenza uniforme della successione ad
implica che la
è integrabile e che vale l’uguaglianza (2.1). _
Sia primitiva di
. La convergenza
della successione
non implica la convergenza della successione
. Questo si vede
facilmente scegliendo
per ogni ,
ed per
ogni .
Le cose cambiano se si assegna il comportamento che le
devono avere in un
medesimo punto :
Teorema 54 Sia
una successione di funzioni continue su un intervallo
e sia
Supponiamo che
e che la successione
converga uniformemente ad .
In tal caso la successione
converge uniformemente alla funzione
Dim. Ricordiamo che la funzione
è continua, come limite uniforme di una successione di funzioni continue. Dunque l’espressione
proposta per ha
senso. La differenza
si stima così:
La successione numerica
tende a zero per ipotesi, mentre la successione numerica
tende a zero per il Teorema 52. L’asserto segue quindi dal Lemma 47. _ Vediamo
ora le relazioni tra derivazione e convergenza uniforme. E’ facile trovare esempi che
mostrano che il limite uniforme di una successione di funzioni derivabili può non essere
derivabile.
Esempio 55 Consideriamo la successione di funzioni
Ciascuna di queste funzioni è derivabile ma la successione
di funzioni converge uniformemente alla funzione non derivabile
.
Il grafico di alcune di queste funzioni è in figura 2.4. _
Vale però:
Teorema 56 Sia
una successione di funzioni derivabili su un intervallo
.
Supponiamo che:
- esista un punto
tale che la successione numerica
converga;
- la successione
converga uniformemente su
ad una funzione .
In tal caso la successione
converge uniformemente su
ad una funzione che è
derivabile, ed inoltre ;
ossia
Dim. Per ipotesi,
L’asserto segue quindi dal Teorema 54. _
2.3 Serie di funzioni
Le serie di funzioni si definiscono in modo del tutto analogo alle serie numeriche: se
é
una successione di funzioni, la serie corrispondente si indica col simbolo
Se é necessario indicare i valori presi dall’indice scriveremo per esempio
Il significato del simbolo di serie é il seguente: supponendo che l’indice prenda tutti i valori
maggiori od uguali a ,
si costruisce la nuova successione
Se la successione di funzioni
converge uniformemente, si dice che la serie converge uniformemente; se la successione di
funzioni
converge in
oppure in ,
si dice che la serie converge in tal senso. Enunciamo il teorema seguente, senza
dimostrarlo:
Teorema 57 Sia convergente la serie di numeri positivi
Valga inoltre
ove
oppure oppure
.
Sotto queste ipotesi, esiste una funzione
(rispettivamente in ,
oppure )
tale che la serie
converge nel senso corrispondente a .
Sia
una serie di funzioni. Si dice che questa serie converge normalmente (in
oppure
in )
quando converge la serie
(con
uguale a ,
).
L’asserto del teorema precedente si esprime anche dicendo che una serie che converge
normalmente è anche una serie convergente. Il viceversa non vale. Nel caso di
, ossia
per la convergenza uniforme, il test per la convergenza dato nel Teorema 57 si
chiama anche test di Weierstrass A parte questo teorema, di dimostrazione diffcile,
i teoremi visti per la convergenza delle successioni di funzioni si adattano
facilmente allo studio della convergenza delle serie. Enunciamo in particolare:
Teorema 58 Una serie di funzioni continue
converga uniformemente su
ad una funzione .
Allora la funzione
è continua e, se
è limitato e chiuso, vale
Sia
una successione di funzioni derivabili, convergente puntualmente su
ad una funzione .
Supponiamo che la serie
converga uniformemente su
ad una funzione .
Allora la funzione
è derivabile, con derivata
ed inoltre la serie
converge ad
uniformemente su .
Esempio 59 Consideriamo la serie
Questa serie converge puntualmente su .
ossia converge per ogni .
Infatti, se
ogni termine della serie è nullo e quindi la somma della serie è ;
se
allora è lecito scrivere
Dunque, si ha
Dunque la somma della serie non è continua e quindi la serie, pur convergendo
puntualmente su ,
non converge uniformemente. _
2.4 Serie di potenze
Si chiamano serie di potenze le serie di funzioni della forma
|
| (2.2) |
ottenute a partire dalla successione di monomi
. Si noti che il primo
valore dell’indice è ora
ma niente vieta che sia
ossia che la serie “parta” per esempio con indice
. Se esiste
tale che
per
, allora la
serie di potenze si riduce ad un polinomio: le serie di potenze generalizzano i polinomi. Il
numero
si chiama il centro della serie e la serie di potenze converge sempre per
(e ivi
converge ad ).
Potrebbe non convergere in nessun altro punto.
Esempio 60 Si consideri la serie seguente, di centro :
Si fissi il valore di
e sia
tale che .
Allora, per ,
si ha
Dunque, se ,
il termine generale della serie non tende a zero, e quindi la serie non converge. _
Vale però:
Teorema 61 (Teorema di Abel) Una serie di potenze converga in un
punto
e sia
Allora, la serie di potenze converge uniformemente in
per ogni .
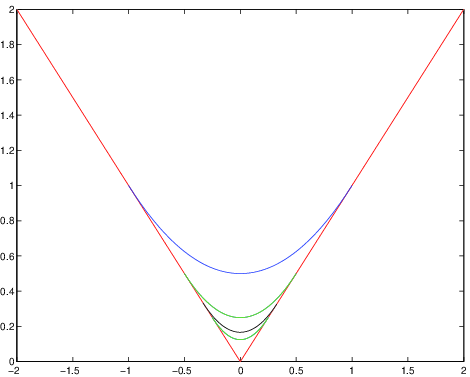
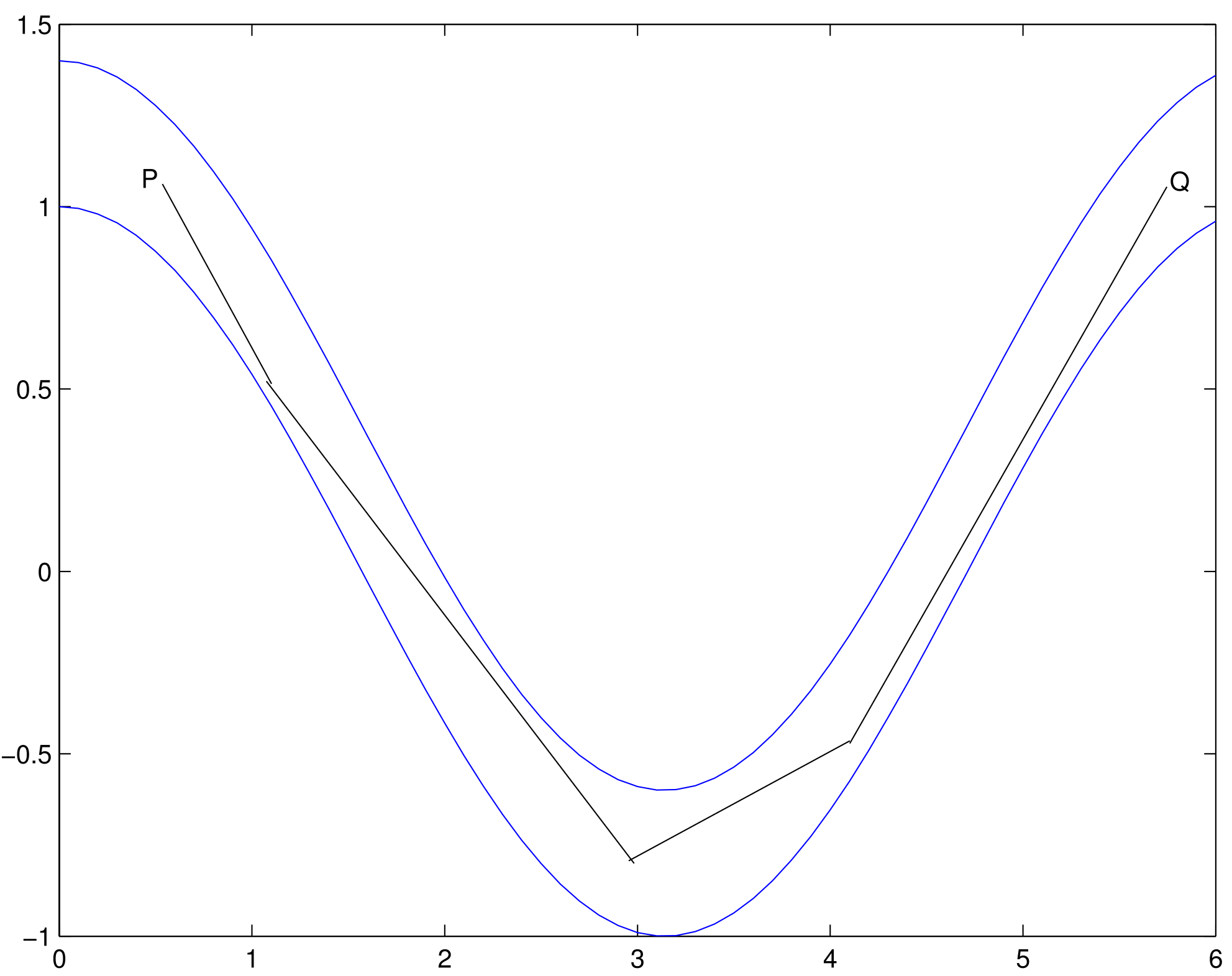
Dim. Si guardi la figura 2.5 per seguire questa dimostrazione.
Sia e
sia
così che
e quindi
La convergenza in
implica che la successione
è limitata (anzi tende a zero):
Inoltre,
Dunque, per
si ha
con e
quindi con .
La convergenza uniforme segue dal criterio di Weierstrass, Teorema 57. _
Questo risultato in particolare implica che se una serie di potenze
converge allora l’insieme su cui essa converge è un intervallo centrato in
(e non si esclude che
sia ridotto al solo ,
oppure che sia tutta la retta). Questo si chiama l’intervallo di convergenza della serie di
potenze e si chiama raggio di convergenza la sua semiampiezza. Il raggio di convergenza
può essere nullo, si veda l’esempio 60. Può essere un numero finito non nullo oppure
può essere :
è un numero finito non nullo nel caso particolare della serie geometrica, è
nel
caso in cui la serie di potenze si riduca ad un polinomio, ma non solo in tal caso:
Osservazione 62 Consideriamo la serie
fissato ,
si trova una serie numerica, convergente per ogni valore del parametro ,
come si vede facilmente usando il criterio del rapporto. _
Inoltre, la dimostrazione del Teorema 61 mostra che:
Teorema 63 (Teorema di Abel) Sia
il raggio di convergenza di una serie di potenze e sia
tale che .
La serie di potenze converge assolutamente e quindi incondizionatamente nel
punto .
Ciò mostra che l’ordine dei termini di una serie di potenze non influisce sulla somma
della serie nei punti interni all’intervallo di convergenza. Invece, niente può dirsi in
generale del comportamento della serie negli estremi dell’intervallo di convergenza,
come mostrano gli esempi seguenti.
Esempio 64 Consideriamo la serie di potenze
fissato si
trova una serie numerica e si vede facilmente, dal criterio del rapporto, che la sere converge
per ogni con
, diverge se
. Dunque il raggio
di convergenza è .
Se
oppure
si trovano rispettivamente le due serie
La prima divergente e la seconda convergente. Si è detto che la somma di una serie
di potenze non dipende dall’ordine degli elementi nei punti interni dell’intervallo di
convergenza. Quest’esempio mostra che, invece, può dipendere dall’ordine degli elementi
se è
uno degli estremi dell’intervallo di convergenza. Mostriamo ora una serie di potenze
che converge in ambedue gli estremi dell’intervallo di convergenza. La serie è
Di nuovo, fissato ,
si usi il criterio del rapporto per studiare la convergenza della
serie numerica che si ottiene. Si vede che si ha convergenza per
, estremi inclusi, mentre
la serie diverge per .
Infine, mostriamo una serie di potenze che diverge in ambedue gli estremi
dell’intervallo di convergenza. Questa è la serie
Questa è una serie geometrica di ragione
e quindi converge
se e solo se ,
estremi esclusi. Si noti che la somma di questa serie è la funzione
una funzione di classe .
La ragione per cui la serie corrispondente non debba convergere
negli estremi sembra misteriosa, e verrà chiarita al paragrafo 2.4.2.
E’ interessante vedere i grafici di alcune delle somme parziali delle
tre serie introdotte sopra. L’intervallo di convergenza delle serie è
.
I grafici delle somme parziali sono disegnati su un intervallo
un po’ più grande e, punteggiato, si riporta anche il
grafico della somma della serie, ovviamente solo sull’intervallo
.
La prima e la seconda serie sono alla figura 2.6
L’ultima serie è alla figura 2.7.
Il grafico punteggiato (tratto spesso) in questo caso rappresenta la funzione
,
che è la somma della serie sul solo intervallo .
E’ stato disegnato in un intervallo più grande per sottolineare che la questa
funzione è regolare anche nei punti
e . _
Inoltre, la convergenza essendo uniforme, dal Teorema 50:
Corollario 65 La somma di una serie di potenze è continua nei punti
interni all’intervallo di convergenza.
Si potrebbe inoltre provare che:
Teorema 66 Sia il raggio
di convergenza della serie .
Le due serie di potenze
|
|
hanno lo stesso raggio di convergenza e questo è uguale ad
.
Le due serie in (2.6) si dicono ottenute derivando termine a termine o integrando
termine a termine la serie data. Esse convergono uniformemente in
e
quindi, usando i teoremi 52 e 56, si trova l’uguaglianza
|
|
In particolare quindi anche la serie derivata può a sua volta venir
derivata termine a termine e ciò tante volte quante si vuole. Dunque:
Corollario 67 La somma di una
serie di potenze di raggio di convergenza non nullo è una funzione di classe
nell’intervallo di convergenza.
Chiediamoci ora come sia possibile calcolare il raggio di convergenza di una serie di
potenze. Esiste una formula per il raggio di convergenza, che non possiamo
presentare. Possiamo però presentare due test particolari, che si ottengono per
confronto con la serie geometrica. Il primo si può applicare quando si ha
per
ogni
(e basta che questa condizione sia soddisfatta per
maggiore di un
opportuno ).
Teorema 68 Supponiamo che
per ogni
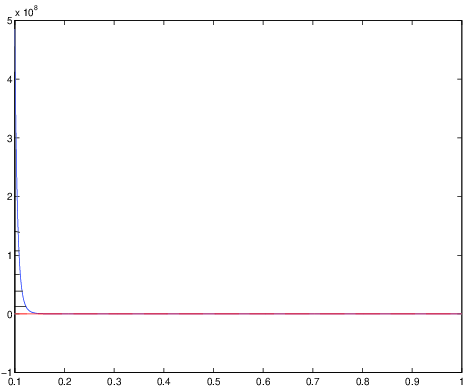
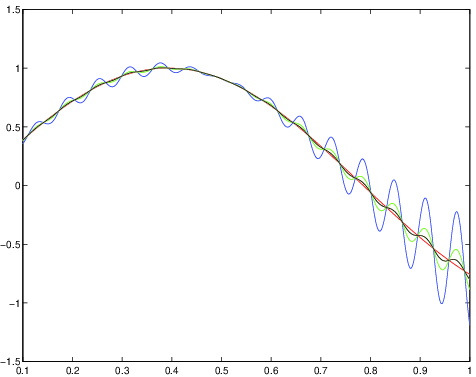
e che esista, finito o meno,
Allora il raggio di convergenza della serie è
Dim. Limitiamoci a considerare il caso .
Applichiamo il criterio del rapporto per la convergenza della serie di numeri
con
fissato. Il criterio del rapporto asserisce che condizione suffciente di convergenza è che
per
suffcientemente grande valga
|
| (2.6) |
La serie diverge se vale la disuguaglianza opposta, con
.
Proviamo che si ha convergenza se
In tal caso,
tale che
|
| (2.7) |
Sia .
Il teorema di permanenza del segno mostra l’esistenza di un numero
tale che
per ogni
vale
Essendo ,
la serie converge (si ricordi (2.6)). In modo analogo si trattano gli altri casi. _
Ripetiamo che il teorema precedente non può usarsi se infiniti coeffcienti
sono
nulli. Usando il criterio della radice invece del criterio del rapporto si prova invece:
Teorema 69 Se esiste, finito o meno, il limite
allora il raggio di convergenza è
Si noti che il Teorema 69 può usarsi anche se infiniti coeffcienti
sono
nulli. Mostriamo ora che esistono serie di potenze il cui raggio di convergenza
non può determinarsi né col criterio del rapporto né con quello della
radice
Esempio 70 Si consideri la serie
E’
Quindi,
E’:
e quindi
In casi di questo tipo, conviene considerare
come una parametro e studiare la convergenza della serie numerica ottenuta,
per ogni valore di .
Usando il criterio della radice per ogni
fissato, si vede che
se
e quindi se ,
per qualche .
Dunque il raggio di convergenza è almeno .
D’altra parte, se
allora per ,
pari, si trova
Quindi, il termine generale non tende a zero e la serie non converge. Quindi, il
raggio di convergenza è uguale ad . _
2.4.1 Operazioni sulle serie di potenze
Le operazioni sulle serie di potenze si eseguono con le regole delle
operazioni sulle serie numeriche, per ogni fissato valore del parametro
. Ci
interessa però notare esplicitamente:
Somma di serie Siano ,
due serie di potenze
col medesimo centro
e con raggio di convergenza rispettivamente
ed
.
Sia
Allora, ambedue le serie convergono per
e
quindi la loro somma può scriversi nuovamente come serie di potenze di centro
, convergente
per :
Il raggio di convergenza della serie somma può essere maggiore di
. Per
esempio, se ,
allora la serie somma ha raggio di convergenza
anche se
. Ciò però può
aversi solamente se .
Infatti, se per esempio
allora .
Infatti, scrivendo
si vede che il raggio di convergenza della prima serie è almeno uguale
a
e questo sarebbe maggiore di
se fosse .
L’operazione di somma può usarsi anche “al contrario” per calcolare il raggio di
convergenza in certi casi nei quali falliscono sia il criterio del rapporto che quello
della radice:
Esempio 71 Torniamo a considerare la serie vista all’esempio 70. La serie
di quest’esempio si può vedere come somma delle due serie
Ora, rinominando
l’indice
della prima serie, si trova
Sostituendo
si trova la serie di potenza
a cui si può applicare sia il criterio del rapporto che quello della radice. Il
raggio di convergenza è
per la serie della variabile ,
e quindi
per la serie della variabile .
Analogamente, la seconda serie converge per .
Dunque, il raggio di convergenza della serie somma è esattamente . _
Unicità della serie di potenze Mostriamo che la serie di potenze che converge ad
una funzione ,
se esiste, è unica:
Teorema 72 Siano
due serie di potenze con raggio di convergenza rispettivamente
ed .
Sia .
Se
per ogni
con
allora
per ogni
e quindi .
Dim. Basta provare che se
per allora
. Posto
si trova
infatti e
quindi l’uguaglianza precedente si scrive
Dunque si ha anche
Calcolando per
si vede e
dunque
Il procedimento può quindi ripetersi trovando
, e
così via. _
Prodotto alla Cauchy di serie di Potenze Consideriamo le due serie di potenze col
medesimo centro
Calcoliamo tutti i possibili prodotti di un termine della prima con un termine della
seconda e raccogliamo i coeffcienti dei termini con la medesima potenza
. Si trova
quando si fa il
prodotto di
con tutti i termini della forma
Ossia, il coeffciente di
viene ad essere
Ciò suggerisce la definizione di prodotto alla Cauchy, definito da
E’ appena il caso di notare che il “nome“ degli indici non ha
effetto sulla somma della serie. Si sono usati “nomi” diversi
(,
ed
) solo
per chiarezza. Il teorema che si può provare è il seguente:
Teorema 73 Due serie di potenze abbiamo raggio di convergenza rispettivamente
ed
coan .
La serie prodotto alla Cauchy ha raggio di convergenza almeno uguale ad
.
Osservazione 74 Consideriamo l’esempio seguente:
Il prodotto alla Cauchy contiene potenze
solo se
può scriversi nella forma
per certi valori di
e .
Il coeffciente di questa potenza è la somma di tanti numeri
quanti sono i modi di scrivere
in tale forma. Ma ora,
e il loro prodotto è
Vedremo, al paragrafo 2.4.3, un modo diverso per rappresentare questa
funzione come somma di una serie di potenze, che calcola i coeffcienti della
(unica!) espansione
in serie di potenze facendo derivate. precisamente vedremo che il coeffciente
di
è
In questo modo, dato ,
si calcola facilmente in quanti modi questo si può rappresentare come somma
di tante “monete” di valore
e tante “monete” di valore . _
2.4.2 Serie di potenze nel campo complesso
Le operazioni algebriche e le operazioni di limite possono anche calcolarsi tra numeri complessi.
Quindi, le serie di potenze possono trattarsi anche nel campo complesso. Il Teorema 61 e il
Teorema 63 si riformulano come segue:
Teorema 75 (Teorema di Abel) Una serie di potenze
nel campo complesso, converge sempre nel punto .
Se converge anche in altri punti, allora essa converge in un disco aperto di centro
e raggio
(si scrive
se la serie converge per ogni ).
La convergenza è uniforme in ogni disco di centro
e raggio ;
è assoluta in ciascun punto
interno al disco di convergenza.
Per convergenza assoluta nel caso di serie di potenze a valori complessi, si intende la convergenza della
serie
La dimostrazione è del tutto analoga a quella vista per le serie di potenze reali. Però, ora può mostrarsi
di più: sia
la somma di una serie di potenze di raggio di convergenza
. Esiste almeno
un punto tale
che , nel quale
la funzione
non è regolare. Ciò chiarisce la stranezza notata all’Esempio 64. Per
vale
e la funzione
è di classe .
Non si vede quindi quale fenomeno possa bloccare la convergenza della serie. Se però la serie si
legge nel campo complesso, allora
e la funzione non è
definita nei punti ,
che distano
dal centro della serie.
2.4.3 Serie di Taylor
Sia una funzione
di classe in un
intorno di .
Ad essa può associarsi la serie di Taylor
Questa si chiama la serie di Taylor della funzione
.
Questa serie può non convergere e, se converge, può non convergere alla funzione
, come
mostra l’esempio seguente:
Esempio 76 Sia
Questa funzione è di classe
su
e le sue derivate in
sono tutte nulle. Dunque la serie di Taylor di centro
associata ad
ha tutti i coeffcienti nulli: converge su
alla funzione identicamente zero e non ad . _
Ci possiamo chiedere quindi sotto quali condizioni la serie di Taylor di
effettivamente converga
ad . Scrivendo la
formula di Taylor di
arrestata all’ordine
e col resto in forma di Lagrange, si vede che
dove dipende
da ed è
compreso tra
ed . La serie di
Taylor converge ad
quando il resto converge a zero. Una condizione perché ciò accada è:
Teorema 77 Esistano ,
tali che
La serie di Taylor di
converge su
e converge alla funzione .
Dim. Ricordiamo che per ogni
si ha
Si osservi ora che
Il membro destro tende a zero e quindi, per il criterio del confronto, tende a zero
uniformemente anche l’errore
La condizione del Teorema 77 è soddisfatta nel caso delle funzioni di cui
correntemente si usano gli sviluppi di Taylor, almeno su un opportuno
intervallo. La tabella seguente riporta alcune funzioni e il raggio di convergenza
della relativa serie di McLaurin (ossia, della serie di Taylor di centro
).
Infine, studiamo la relazione tra parità di una funzione e sua serie di Taylor. Vale:
Teorema 78 Sia
f(x) = ∑
n=0+∞a
nxn.
La funzione è pari se e solo se sono nulli i coeffcienti
an
di indice dispari; la funzione è dispari se e solo se sono nulli i coeffcienti
an
di indice pari.
Dim. Sia f(x)
sviluppabile in serie di Taylor. Se è dispari, essa si annulla in
0. Dunque
a0 = 0.
La sua derivata prima è pari ma la derivata seconda è dispari e quindi
f″(0) = 0 ossia vale
anche a2 = 0.
Iterando questo procedimento si vede che ogni
a2k è nullo.
Se f(x) è
pari, sono dispari tutte le sue derivate di ordine dispari e quindi sono nulli gli
a2k+1. Il
viceversa è ovvio. _
2.4.4 Serie di potenze ed equazioni differenziali lineari
Consideriamo il problema di Cauchy
x′ = ax,x(0) = x
0.
Il coeffciente a è costante.
Per definizione, la soluzione x
è continua e quindi, dall’uguaglianza, è addiritture continuamente derivabile; e
quindi
x″ = ax′ = a2x.
Così proseguendo,
x(n) = anx
e quindi, per t = 0,
x(n)(0) = anx
0.
Dunque, la soluzione x(t)
è di classe C∞
e verifica le condizioni del Teorema 77 su tutti gli intervalli chiusi contenenti
x0.
Dunque, la soluzione si esprime in forma di serie di potenze
x(t) = ∑
n=0+∞ 1
n!antn
D’altra parte si verifica immediatamente che questa è la serie dell’esponenziale e
quindi si ritrova il risultato noto
x(t) = eatx
0.
Consideriamo ora il sistema di equazioni differenziali lineari
ove x→ è un
vettore di ℝn ed
A è una matrice
n × n che è costante, ossia
non dipende n’e da t
n’e da x.
Vogliamo rappresentare la soluzione di questo sistema che verifica l’ulteriore
condizione
x→(t0) = x→0.
E’ facile vedere che tutto ciò che abbiamo detto sulle serie di potenze e sulle serie
di Taylor si estende senza cambiamenti a funzioni a valori vettori o matrici e quindi
è ancora vero che
x→(t) = ∑
n=0+∞ 1
n!An(t − t
0)n x→
0.
Questa serie si indica col simbolo
|
eA(t−t0) = ∑
n=0+∞ 1
n!An(t − t
0)n.
| (2.9) |
Ciò definisce l’esponenziale di una matrice, e la (2.9) rappresenta in forma
compatta le soluzioni dell’equazione differenziale lineare a coeffcienti costanti (2.8):
Osservazione 79 Va notato un fatto importante: l’esponenziale di matrice
può essere un polinomio. Per esempio, se
A = 01 0 0
allora
A2 = 0
e quindi
eAt = 1t
10 :
eAt
è un polinomio di primo grado. Si prova invece che se
A = 0 1 − 1 0
allora
eAt = cos t sin t
− sin t cos t .
Proprietà importanti della matrice esponenziale
eAt sono
espresse dal teorema seguente, che non proviamo:
Teorema 80 Vale:
- AeAt = eAtA.
- det eA = exp{∑
i=1na
ii}.
Dunque, det eA
è sempre diverso da zero: la matrice eA
è invertibile per ogni A.
- eA −1 = e−A.
- Se AB = BA
allora eAeB = eA+B.
In particolare, vale sempre eAteAt′ = eA(t+t′).
- La funzione t → eAt
è derivabile e
d
dteAt = AeAt.
L’introduzione dell’esponenziale eAt
della matrice At
permette anche di rappresentare la soluzione del problema
x→′ = Ax→ + f→(t)x→(t
0) = x→0.
Procediamo esattamente come già si è visto (nel corso di Analisi
Matematica 1) per l’equazione scalare: moltiplicando i due membri per
e−At si
trova
|
e−Atx→′(t) − Ae−Atx→(t) = e−Atf→(t).
| (2.10) |
La regola della derivata del prodotto si estende al prodotto di una matrice per un
vettore
e quindi la (2.10) è
d
dt e−Atx→(t) = e−Atf→(t).
Integrando i due membri da t0
a t si
trova
|
e−Atx→(t) − e−At0
x→0 = ∫
t0te−Asf→(s)ds.
| (2.11) |
Moltiplichiamo i due membri di (2.11) per
eAt e
usiamo le proprietà nel teorema 80. Si trova
x→(t) = eA(t−t0)x→
0 + ∫
0teA(t−s)f→(s)ds.
2.5 Serie di Fourier: introduzione
Oltre alle serie di potenze, nelle applicazioni si incontrano molti altri tipo di “serie
di funzioni”, la cui teoria comunque è sostanzialmente più complessa e viene qui
esaminata per sommi capi nel caso di gran lunga più importante delle serie di
Fourier. Si chiamano serie di Fourier le serie del tipo
|
a0 + ∑
n=1+∞a
n cos nπ
Lx + bn sin nπ
Lx.
| (2.12) |
I coeffcienti an
e bn sono
reali. Se L = π
si trova
a0 + ∑
n=1N a
n cos nx + bn sin nx.
Si noti che, usando sin 0x = 0, si potrebbe
assorbire il coeffciente a0
nella serie scritta con n ≥ 0
invece che con n ≥ 1.
Vedremo che c’è una buona ragione per separare
a0 dagli
an con
n > 0.
Ovviamente una serie di Fourier non sempre converge. La
convergenza sarà implicata da opportune proprietà dei coeffcienti
an e
bn.
Per esempio, certamente si ha convergenza (uniforme) quando
an = bn = qn, con
|q| < 1. Il
problema della convergenza puntuale o uniforme delle serie di Fourier comunque è assai
delicato e lo illustreremo più avanti. Per ora notiamo che se la serie converge per un
x0 ∈ [−L,L] allora essa converge
in ogni punto x0
di forma x0 + 2kL con
k intero; e se converge
per ogni x ∈ [−L,L] essa
converge per ogni x ∈ ℝ
e converge ad una funzione peridica di periodo
T = 2L. Per
questa ragione, prima di studiare le serie di Fourier, vogliamo richiamare alcune
proprietà delle funzioni periodiche.
2.5.1 Premesse: le funzioni periodiche
Sia f(x) una funzione
della variabile reale x.
Si dice che f(x) è
periodica di periodo T
quando:
- E’ T≠0.
- la funzione f(x)
è definita in x + T
se e solo se è definita in x.
E’ conseguenza di questo che la funzione è definita in x + nT
(ove n
è intero qualsiasi) se e solo se è definita in x.
- per ogni x
nel dominio della funzione, si ha f(x) = f(x + T)
e quindi anche f(x) = f(x + nT)
per ogni numero intero n.
Teorema 81 Sia f(x)
periodica di periodo T
e sia S
numero reale. La funzione f(Sx)
ha periodo T∕S.
In particolare, se S = T∕(2π),
la funzione ha periodo 2π.
La verifica è immediata:
f(S(x + T∕S)) = f(T + Sx) = f(Sx).
Una funzione periodica non ha un solo periodo: se
T è un periodo
anche 2T,
−T,
−2T ecc. sono
periodi. L’insieme dei periodi positivi ha però un estremo inferiore che può essere
nullo.
Molto spesso, quando si parla di “periodo” di una funzione periodica si
intende che esista un minimo periodo positivo, e per periodo si intende tale
numero. Se
T è il (minimo)
periodo di f(x), allora
1∕T si chiama la
frequenza di f(x) mentre
2π∕T si chiama la frequenza
angolare di f(x). Per
esempio, le funzioni sin ωx e
cos ωx sono funzioni periodiche
di periodo 2π∕ω ovunque
definite mentre tan ωx è una
funzione di periodo π∕ω,
che però non è ovunque definita.
Osservazione 82 Vediamo come i concetti precedenti si applicano alla serie
di Fourier (2.12). Le funzioni cos n(π∕L)x
e sin n(π∕L)x
hanno (minimo) periodo 2L∕n
e quindi tutti i termini della serie di Fourier hanno periodo (non necessariamente
minimo) T = 2L.
Per questa ragione potremo limitarci a studiare la serie di Fourier sull’intervallo
[−L,L]
o su un qualsiasi altro intervallo di lunghezza 2L,
per esempio [0, 2L].
La frequenza di cos n(π∕L)x
e sin n(π∕L)x
è n∕2L
mentre la loro frequenza angolare è
2π 1
T = nπ
L :
il coeffciente di x
nei due termini in posizione n
della serie di Fourier è la frequenza angolare nπ∕L. _
Vale:
Teorema 83 Sia f(t)
continua su ℝ
e periodica di periodo T.
Per ogni x ∈ ℝ
si ha
∫
0T f(s)ds = ∫
xx+T f(s)ds,∫
0T f(x + s)ds = ∫
0T f(s)ds.
Dim. Conviene provare la prima uguaglianza in due passi:
-
- Passo 1. Proviamo che per ogni k
intero si ha:
∫
0T f(s)ds = ∫
kT (k+1)T f(s)ds;
ossia proviamo l’uguaglianza richiesta nel caso particolare x = kT.
Per questo sostituiamo s = kT + r
nell’integrale a destra. Si trova
∫
kT (k+1)T f(s)ds = ∫
0T f(kT + r)dr = ∫
0T f(r)dr.
L’ultima uguaglianza vale perché la funzione è periodica di periodo
T
e quindi f(kT + r) = f(r).
-
- Passo 2. Consideriamo ora il caso generale
kT < x < (k + 1)T < x + T.
Proviamo che vale
∫
xx+T f(s)ds = ∫
kT (k+1)T f(s)ds.
Ciò fatto, l’uguaglianza richiesta seguirà dal passo 1. Per capire questa
parte del calcolo, si guardi la figura 2.8. Come suggerito dalla figura,
scriviamo
|
∫
xx+T f(s)ds = ∫
x(k+1)T f(s)ds + ∫
(k+1)T x+T f(s)ds.
| (2.13) |
La sostituzione s = T + r
mostra che
∫
(k+1)T x+T f(s)ds = ∫
kT xf(T + r)dr = ∫
kT xf(r)dr.
L’ultima uguaglianza vale perché
f(x) è periodica
di periodo T
e quindi f(r) = f(T + r).
Tornando alla (2.13) si vede che
∫
xx+T f(s)ds = ∫
x(k+1)T f(s)ds + ∫
kT xf(r)dr = ∫
kT (k+1)T f(r)dr,
come volevamo provare.
La seconda uguaglianza è conseguenza della prima perché
∫
0T f(x + s)ds = ∫
xx+T f(r)dr = ∫
0T f(r)dr.
Si noti che nel teorema precedente T
non è necessariamente il minimo periodo. _
2.5.2 Premesse: le formule d’Eulero
Ricordiamo le formule d’Eulero, incontrate nello studio delle equazioni differenziali
lineari:
eix = cos x + i sin x
e quindi
e−ix = cos x − i sin x.
Osservazione 84 Le formule d’Eulero mostrano che la funzione x → eix
è periodica di periodo 2π.
E’ anche vero che l’estensione della funzione esponenziale al piano complesso
ex+iy = ex(cos y + i sin y)
è periodica di periodo 2πi,
ossia è periodica quando il suo argomento si muove parallelamente all’asse immaginario. _
Sommando e sottraendo membro a membro, si trovano le uguaglianze
sin x = eix − e−ix
2i , cos x = eix + e−ix
2 .
Anch’esse vanno sotto il nome di formule d’Eulero Sostituendo queste espressioni
in
a0 + ∑
n=1N a
n cos nx + bn sin nx
si trova (si ricordi che −i = 1∕i)
a0 + ∑
n=1Nan − ibn
2 einx + ∑
n=1Nan + ibn
2 e−inx = ∑
n=−NNc
neinx
ove ora i cn
sono i numeri complessi
|
c0 = a0
cn = an−ibn
2 sen > 0
cn = an+ibn
2 sen < 0
| (2.14) |
e quindi tali che
c−n = c̄n.
Si osservi che anche in questa scrittura il termine con
n = 0 ha un ruolo
particolare: c0 = c̄0
è reale. Sostituendo in
|
a0 + ∑
n=1N a
n cos nπ
Lx + bn sin nπ
Lx
| (2.15) |
si trova
|
∑
n=−NNc
nein(π∕L)x
| (2.16) |
con i coeffcienti cn
ancora dati da (2.14) e quindi con
|
c−n = c̄n,e c0 = c̄0.
| (2.17) |
E’ facile vedere che si fa anche il passaggio inverso: se valgono le (2.17) allora
nella (2.16) i termini puramente immaginari si elidono e la somma (2.16) si riduce
a (2.15), con coeffcienti reali. Un’espressione della forma (2.16) si chiama un
polinomio trigonometrico Se valgono le (2.17), il polinomio trigonometrico (2.16) si
può scrivere nella forma “reale” (2.15). L’espressione (2.15) è una somma
parziale della serie di Fourier (2.12). Per questa ragione, la serie di Fourier (2.12) si
può anche scrivere in “forma complessa”,
|
∑
n−=∞+∞c
nein(π∕L)x.
| (2.18) |
Il fatto importante da ricordare è che se vogliamo che questa serie corrisponda
alla (2.12) le somme parziali vanno prese in modo simmetrico: le somma parziali sono
|
∑
n=−NNc
nein(π∕L)x
| (2.19) |
e non
|
∑
n=−KNc
nein(π∕L)x
| (2.20) |
con K
ed N
tra loro indipendenti. E infatti può accadere che per
K →−∞ ed
N → +∞,
indipendentemente, la (2.20) non ammetta limite nemmeno se (2.19) ammette limite
per N → +∞.
Avremo bisogno di calcolare derivate e integrali di funzioni
f(x) + ig(x)
della variabile reale x,
a valori numeri complessi. Per definizione,
d
dx[f(x)+ig(x)] = f′(x)+ig′(x),∫
ab[f(x)+ig(x)]dx = ∫
abf(x)dx+i∫
abg(x)dx
e quindi
∫
ab d
dx[f(x) + ig(x)]dx = [f(b) + ig(b)] − [f(a) + ig(a)].
Essendo
d
dxeinx = ineinx,
si trova:
|
∫
−ππ cos nx cos mxdx = 2πsen = m = 0 0 se n≠ m
π sen = m≠0
∫
−ππ sin nx cos mxdx =0 per ogni n, m.
∫
−ππ sin nx sin mxdx = 0sen≠m π se n = m
| (2.21) |
Per verificare la prima delle uguaglianze precedenti (con
n≠m)
calcoliamo, usando le formule d’Eulero
|
∫
−ππ cos nx cos mxdx = 1
4 ∫
−ππ einx + e−inx eimx + e−imx dx
= 1
4 ∫
−ππ ei(n+m)x + ei(n−m)x + e−i(n+m)x + e−i(n−m)x dx.
|
L’asserto ora segue perchè, essendo per esempio
d
dxei(n+m)x = i(n + m)ei(n+m)x,
si ha
∫
−ππei(n+m)xdx = 1
i(n + m) ei(n+m)π − e−i(n+m)π = 2
n + m sin((n+m)π) = 0.
Le altre uguaglianze si provano in modo analogo.
Osservazione 85 a queste conclusioni si può arrivare in modo più
elementare se si ricordano le formule di Werner. il primo integrale si può
calcolare ricordando che
[cos nx][cos mx] = 1
2 cos(n + m)x + cos(n − m)x.
Più in generale, su un intervallo [−L,L]
vale
|
∫
−LLein(π∕L)xdx = 2Lsen = 0
0 sen≠0
∫
−LL cos nx cos mxdx = 2Lsen = m = 0 0 se n≠ m
L sen = m
∫
−LL sin nx cos mxdx =0 per ogni n, m.
∫
−LL sin nx sin mxdx = 0 sen≠m
Lsen = m
| (2.22) |
Le uguaglianze precedenti mostrano che le funzioni
1
2L, 1
L cos nπ
Lx, 1
L sin nπ
Lx,
equivalentemente
1
2Lein(π∕L)x,
sono due a due ortogonali in ℒ2(−L,L)
e tutte di norma uguale ad 1.
Si dice brevemente che sono sistemi ortonormali in
ℒ2(−L,L).
Quest’osservazione suggerisce che l’ambiente in cui è più facile studiare la serie di Fourier
sia lo spazio ℒ2(−L,L) e
non lo spazio C(−L,L).
2.6 La serie di Fourier in ℒ2(−L,L)
Non è stato possibile introdurre in modo rigoroso lo spazio
ℒ2(−L,L) e ciò
indica che lo studio della serie di Fourier è molto più complesso di quello delle
serie di potenze, e può essere solo accennato. Consideriamo il polinomio
trigonometrico
|
∑
n=−NNc
nein(π∕L)x,c
n = c̄−n
| (2.23) |
equivalentemente, se cn = an + ibn = c̄−n,
|
a0 + ∑
n=1N a
n cos n(π∕L)x + bn sin n(π∕L)x.
| (2.24) |
Indichiamo questo polinomio trigonometrico col simbolo
P(x). Ovviamente,
P(x) è una funzione
continua e periodica su ℝ.
Se i valori di P(x)
su [−L,L]
si conoscono, da questi si ricavano facilmente i coeffcienti
cn ed i
coeffcienti an
e bn.
Infatti, moltiplicando i due membri dell’uguaglianza
P(x) = ∑
n=−NNc
nein(π∕L)x
per e−ir(π∕L)x e
integrando su [−L,L]
si trova 0
se r≠N.
Altrimenti si trova
cr = 1
2L∫
−ππP(x)e−ir(π∕L)xdx.
Analogamente,
a0 = 1
2L ∫
−LLP(x)dx
ak = 1
L ∫
−LLP(x) cos k(π∕L)xdx(se k > 0)
bk = 1
L ∫
−LLP(x) sin k(π∕L)xdx.
(ossia, la formula per a0
non si ottiene da quella di ak
ponendo k = 0. Per questa
ragione conviene scrivere a0
separato dalla sommatoria). Vale inoltre:
Teorema 86 E’:
|
1
2L∫
−LL|P(x)|2dx = ∑
n=−N+N|c
n|2
1
2L∫
−LL|P(x)|2dx = a
02 + 1
2 ∑
n=1+∞a
n2 + b
n2 .
| (2.25) |
L’identità precedente va sotto il nome di Identità di Parseval Si noti il significato di
a0 e di
c0: questi numeri sono
le medie integrali di P(x).
Analogamente, il membro sinistro dell’identità di Parseval è la media integrale di
|P(x)|2. Sia ora
f(x) ∈ℒ[−L,L]. Chiamiamo coeffcienti
di Fourier della funzione f(x)
i numeri
|
cr = 1
2L∫
−LLf(x)e−ir(π∕L)xdx
| (2.26) |
(se vogliamo scrivere la serie di Fourier con gli esponenziali complessi),
|
a0 = 1
2L ∫
−LLf(x)dx
ak = 1
L ∫
−LLf(x) cos k(π∕L)xdx(se k > 0)
bk = 1
L ∫
−LLf(x) sin k(π∕L)xdx
| (2.27) |
(se vogliamo scrivere la serie di Fourier nel campo reale). Si chiama serie di Fourier associata
alla funzione f(x)
la serie (2.12) con i coeffcienti dati da (2.27) o, equivalentemente, la serie (2.18)
con i coeffcienti dati da (2.26). Per fissare le idee e scrivere formule più semplici,
usiamo ora la serie di Fourier scritta mediante gli esponenziali complessi.
Considerazioni del tutto analoghe valgono anche per la serie di Fourier scritta nel
campo reale. Consideriamo la serie
∑
−∞+∞c
neinx
e la sua somma parziale N–ma
SN(x) = ∑
−N+Nc
neinx.
Si noti che SN(x)
è il polinomio trigonometrico (2.23) e che, se
cn = an + ibn = c̄−n,
allora SN(x)
può scriversi nella forma (2.24). Si può provare:
Teorema 87 Sia f ∈ℒ2(−L,L).
Vale:
lim N→+∞∫
−LL f(x) − S
N(x) 2dx = 0ossia lim
N→+∞||f − SN||ℒ2(−L,L) = 0.
Inoltre, la serie converge incondizionatamente, ossia la serie converge, e
sempre alla medesima funzione f(x),
anche riordinandone i termini.
Dunque, la successione delle somme parziali
(SN(x)) converge
ad f(x) nella
distanza di ℒ2(−L,L).
Sottolineiamo nuovamente che il teorema riguarda
SN(x) e non per esempio una
somma ∑
n=−Kn=Nc
nein(π∕L)x. Anche se i
cn sono i coeffcienti
di Fourier di f,
niente può dirsi del comportamento di questa serie per
N → +∞,
K → +∞
in modo indipendente. Diamo un’interpretazione geometrica di
SN(x). Consideriamo il
sottospazio lineare 𝒱N,
𝒱N = ∑
n=−N+Nγ
nein(π∕L)x,γ
n = γ̄−n,γn ∈ ℂ
Che è uno spazio vettoriale di dimensione
2N + 1. Si
ha:
Teorema 88 La somma parziale SN(x)
di f(x)
è l’elemento di 𝒱N
che ha minor distanza da f(x)
nel senso della distanza di ℒ2(−L,L).
Dim. Facciamo la dimostrazione nel caso
N = 1.
La dimostrazione nel caso generale è analoga. Gli elementi dello spazio
𝒱1 sono
le funzioni
γ0 + γ1eix + γ̄
1e−ixγ
i ∈ ℂ,
equivalentemente
α0 + α1 cos(π∕L)x + β1 sin(π∕L)x,α0,α1,β1 ∈ ℝ.
Tra queste funzioni dobbiamo trovare quella che ha minima distanza da
f(x). Si
tratta quindi di studiare un problema di minimo al variare dei parametri complessi
γ0 e
γ1
o, equivalentemente, al variare dei parametri reali
α0,
α1,
β1. Dato
che i problemi di minimo che si sono studiati sono quelli di funzioni di variabile
reale, conviene studiare il minimo della funzione
Φ(α0,α1,β1) = ∫
−LL[f(x) − α
0 − α1 cos(π∕L)x − β1 sin(π∕L)x]2dx.
Il minimo esiste, come conseguenza del Teorema di Weierstrass, perché la
funzione
(α0,α1,β1)→Φ(α0,α1,β1)
è continua e tende a +∞ per
||(α0,α1,β1)||→ +∞. Per trovarlo, annulliamo
le derivate prime.
Si trovano le condizioni
|
∫
−LL[f(x) − α
0 − α1 cos(π∕L)x − β1 sin(π∕L)x]dx = 0
∫
−LL[f(x) − α
0 − α1 cos(π∕L)x − β1 sin(π∕L)x] cos(π∕L)xdx = 0
∫
−LL[f(x) − α
0 − α1 cos(π∕L)x − β1 sin(π∕L)x] sin(π∕L)xdx = 0.
|
Usando le uguaglianze (2.21), si trova che le tre derivate parziali si annullano
solamente quando
|
α0 = (1∕2L) ∫
−LLf(x)dx
α1 = (1∕L) ∫
−LLf(x) cos xdx
β1 = (1∕L) ∫
−LLf(x) sin xdx;
|
ossia, il punto di 𝒱1
che meno dista da f(x)
è S1(x). _
Dunque l’interpretazione della serie di Fourier in
ℒ2(−L,L) è la seguente: per
ogni N si considera
il sottospazio 𝒱N di
dimensione finita 2N + 1
di ℒ2(−L,L). Si scrive la serie
di Fourier di f(x) e si
tronca all’indice N. Si
trova un elemento di 𝒱N
che è proprio l’elemento che meglio approssima la funzione
f(x) nel senso
di ℒ2(−L,L).
Usando una terminologia della geometria elementare, diremo che
SN(x) è la proiezione
ortogonale di f(x)
su 𝒱N. Il
Teorema 87 si può riassumere dicendo che la successione delle proiezioni di
f sui
𝒱N converge
ad f in
ℒ2(−L,L).
Diciamo infine che l’identità di Parseval vale per ogni
f(x) ∈ℒ2(−L,L):
1
2L∫
−LL|f(x)|2dx = ∑
n=−∞+∞|c
n|2
ossia
1
2L∫
−LL|f(x)|2dx = a
02 + 1
2 ∑
n=1+∞[a
n2 + b
n2].
Di conseguenza:
Teorema 89 La successione dei coeffcienti di Fourier tende a zero.
L’identità di Parseval ha un’interpretazione importante per le applicazioni, che
illustriamo con riferimento alla forma complessa, che scriviamo come:
∫
−LL|f(x)|2dx = 2L ∑
n=−∞+∞|c
n|2 .
Interpretiamo la variabile x
come “posizione” ed f(x)
come “velocità”. Il primo integrale si interpreta come “energia” per esempio cinetica:
la “somma” delle energie associate ad ogni particella del corpo. La “componente” di
frequenza n∕2L,
ossia
cnein(π∕L)x
ha quindi “energia” 2L|cn|2.
Quindi,
l’energia totale ottenuta sommando le energie in tutte le posizioni è
uguale alla somma delle energie delle componenti di tutte le frequenze.
Naturalmente, niente vieta che nella rappresentazione di un segnale
f(x) la componente di
frequenza n0∕2L abbia
“energia” nulla, ossia che cn0 = 0.
Le considerazioni precedenti mostrano che l’energia di
f(x) si ripartisce
tra i segnali einx
per cui cn≠0. La
successione (n∕2L,cn)
si chiama lo spettro del segnale. Infine, notiamo che l’identità di Parseval mostra
che se i coeffcienti di Fourier sono tutti nulli allora la funzione è nulla, ed
ovviamente vale anche il viceversa. Ossia:
Teorema 90 Due funzioni f,
g in
ℒ2(−L,L) con i
medesimi coeffcienti di Fourier verificano
|
∫
−LL f(x) − g(x) 2dx = 0.
| (2.28) |
Se accade che le due funzioni f(x)
e g(x)
sono continue, allora la condizione (2.28) implica che esse coincidono. In
generale, se vale (2.28), le due funzioni possono “considerarsi equivalenti” nel
senso che danno il medesimo contributo alle espressioni integrali nelle quali
figurano.
Il calcolo dei coeffcienti di Fourier
Il calcolo dei coeffcienti di Fourier richiede il calcolo di integrali piuttosto noiosi. In
certi casi si possono usare dei trucchi che semplificano il calcolo. Per esempio:
- Il prodotto di una funzione pari e di una dispari è dispari; e una funzione
dispari ha integrale nullo su [−L,L].
Dunque, se f(x)
è dispari, i coeffcienti an
sono tutti nulli. Analogamente, se f(x)
è pari i coeffcienti bn
sono tutti nulli.
- Si voglia calcolare la serie di Fourier della funzione f(x) = x.
Questa è una funzione dispari e quindi vanno calcolati i soli coeffcienti
bn,
bn = 1
L∫
−LLx sin nπ
Lxdx.
Questi integrali si calcolano facilmente per parti ma ciò richiede un
calcolo indipendente per ogni valore di n.
Un modo più veloce è il seguente: si consideri la funzione
s→x sin sxossias→ − d
ds cos sx.
Il numero Lbn è
il valore per s = nπ∕L
della funzione
|
−∫
−LL d
ds cos sxdx = −d
ds∫
−LL cos sxdx =
− d
ds 2
s sin sL = 2
s2 sin sL −2L
s cos sL
|
(formula valida per s≠0).
Calcolando per s = nπ∕L e
dividendo per L,
si trova
bn = 2(−1)n+1 L
nπ.
Dunque,
|
x = 2L
π∑
n=1+∞(−1)n+1
n sin nπ
Lx.
| (2.29) |
Procedendo in modo analogo si verifichi che
x2 = L2
3 −4L2
π2 ∑
n=1+∞(−1)n
n2 cos nπ
Lx.
- Generalmente non è lecito derivare termine a termine una serie di Fourier. Invece, se
f(x) ∈ℒ2(−L,L), la serie di
Fourier di f(x)
può integrarsi termine a termine: se
f(x) = a0 + ∑
n=1+∞a
n cos n(π∕L)x + bn sin n(π∕L)x
allora
|
F(x) = ∫
0xf(s)ds = a
0x + L
π∑
n=1+∞bn
n
+ L
π∑
n=1+∞an
n sin n(π∕L)x −bn
n cos n(π∕L)x.
|
Si noti che quella ottenuta non è una serie di Fourier, a causa del primo addendo
a0x. Se vogliamo la
serie di Fourier di F(x)
dobbiamo esprimere anche la funzione
x
mediante la sua serie di Fourier, usando (2.29). In questo modo si trova
|
F(x) = L
π∑
n=1+∞bn
n
+ L
π∑
n=1+∞2(−1)n+1a
0 + an
n sin n(π∕L)x −bn
n cos n(π∕L)x.
|
2.6.1 Estensioni pari e dispari, e serie di Fourier
Il fatto seguente si è già notato: la funzione
f(x) sia
pari,
f(x) = f(−x).
In questo caso, ciascuna delle funzioni
f(x) sin nx
è dispari e quindi ha integrale nullo: i coeffcienti
bn
sono tutti nulli. Ovviamente, vale anche il viceversa se i coeffcienti
bn sono
tutti nulli, la somma della serie è una funzione pari. Analogamente, se
f(x) è
dispari,
f(x) = −f(−x),
sono nulli i coeffcienti an
e viceversa. Dunque:
Teorema 91 Sia
f(x) = a0 + ∑
n=1+∞a
n cos nπ
Lx + bn sin nπ
Lx.
La funzione f(x),
periodica di periodo T = 2L,
è pari se e solo se bn = 0
per ogni n;
è dispari se e solo an = 0
per ogni n.
Supponiamo ora che sia data una funzione
f(x) definita
solamente su [0,L].
Ad essa possono associarsi infinite serie di Fourier, una per ciascuna “arbitraria” estensione
di f(x) a
[−L, 0]. Tra
queste estensioni due sono privilegiate: l’estensione pari e l’estensione dispari.
L’estensione pari conduce ad una serie di soli coseni mentre l’estensione dispari
conduce ad una serie di soli seni. Dunque:
Teorema 92 Sia f(x) ∈ℒ2(0,L).
Essa è somma di un’unica serie di Fourier di soli seni, e di un’unica serie di
Fourier di soli coseni. La prima definisce l’unica estensione dispari di f(x)
ad ℝ,
periodica di periodo 2L;
la seconda definisce l’unica estensione pari di f(x)
ad ℝ,
periodica di periodo 2L.
Le formule per la serie di Fourier di f(x)
di soli seni e di soli coseni si ottengono scrivendo nelle (2.27) le opportune estensioni di
f(x). Per esempio, usando
l’estensione pari, per k≠0
si trova
ak = (1∕L) ∫
−LLf(x) cos k(π∕L)xdx = 2
L∫
0Lf(x) cos k(π∕L)xdx.
Dato che queste formule (e la corrispondente identità di Parsevale) sono
di uso molto comune, vanno ricordate. E’ bene quindi scriverle in modo
esplicito:
Sviluppo di Fourier in soli coseni
Sia f(x) ∈ℒ2(0,L).
Si ha:
f(x) = α0 + ∑
n=1+∞α
n cos n(π∕L)x
con
|
α0 =(1∕L) ∫
0Lf(x)dx
αn =(2∕L) ∫
0Lf(x) cos n(π∕L)xdx(se n > 0)
| (2.30) |
La corrispondente identità di Parseval è
1
L∫
0L|f(x)|2dx = α
02 + ∑
n=1+∞α
n2 = ∑
n=0+∞α
n2.
Sviluppo di Fourier in soli seni
Sia f(x) ∈ℒ2(0,L).
Si ha:
f(x) = ∑
n=1+∞β
n sin n(π∕L)x
con
|
βn = (2∕L) ∫
0Lf(x) sin n(π∕L)xdx.
| (2.31) |
La corrispondente identità di Parseval è:
1
L∫
0L|f(x)|2dx = ∑
n=1+∞β
n2.
Osservazione 93 Sia f(x) = cos(π∕L)x,
definita su [0,L].
Vogliamo calcolarne lo sviluppo di Fourier in soli coseni ed in soli seni. Lo
sviluppo di Fourier in soli coseni è
f(x) = cos(π∕L)x.
Invece, per lo sviluppo di Fourier di soli seni dobbiamo calcolare i coeffcienti
bn
usando la formula (2.30). Ricordiamo la formula di Werner seguente:
(sin a)(cos b) = 1
2 sin(a + b) + sin(a − b) .
Si trova:
|
βn = 2
L∫
0L cos(π∕L)x sin n(π∕L)xdx
= 1
L∫
0L sin π
L(n + 1)x + sin π
L(n − 1)xdx
= − 1
π(n + 1) cos π(n + 1) − 1 − 1
π(n − 1) cos π(n − 1) − 1
= 4
π n
n2−1se n è pari
0 se n è dispari.
|
Dunque,
cos π
Lx = 8
π∑
k=1+∞ k
4k2 − 1 sin 2kπ
Lx,0 < x < L.
E’ questa la serie di Fourier dell’estensione per periodicità della funzione
f(x)
seguente, il cui grafico (con L = 3)
è riportato in figura 2.9.
|
f(x) = cos π
Lx se 0 < x < L − cos π
Lxse − L < x < 0
| (2.32) |
2.7 La convergenza puntuale della serie di Fourier
E’ un fatto che la convergenza nel senso della norma di
ℒ2(−L,L)
non implica la convergenza puntuale, nemmeno in un solo punto.
Anzi, si prova che esistono funzioni continue e periodiche su
[−L,L] la cui
serie di Fourier non converge. Esistono però anche casi in cui la serie di Fourier
converge puntualmente. Come abbiamo detto questo accade se, per esempio,
an = bn = qn con
|q| < 1.
Ci si può chiedere se sia possibile dare condizioni sulla funzione
f(x) che
implichino la convergenza puntuale della serie di Fourier. Condizioni per questo
sono note. In particolare si ha:
Teorema 94 Sia (a,b) ⊆ [−L,L]
ed esistano M e
α ∈ [0, 1] tali che per
ogni coppia x,
y di punti
di (a,b)
valga
|
|f(x) − f(y)| < M|x − y|α.
| (2.33) |
Sia [a′,b′] ⊆ (a,b). La serie
di Fourier di f(x)
converge ad f(x)
uniformemente in [a′,b′].
Una funzione f(x)
ovunque derivabile con derivata limitata,
|f′(x)| < M,
in particolare verifica
|f(x) − f(y)| < M|x − y|
e quindi soddisfa alle condizioni del teorema. D’altra parte le
ipotesi del teorema 94 implicano la continuità della funzione
f(x) e
questa è una condizione eccessivamente restrittiva per molte applicazioni
nelle quali interviene la serie di Fourier. Per cercare di indebolire
quest’ipotesi, studiamo cosa accade vicino ad un punto di salto di
f(x). Vale:
Vale:
Teorema 95 La funzione f(x) ∈ℒ2(−L,L)
abbia un salto nel punto x0.
Supponiamo inoltre che esistano a < x0
e b > x0
tali che f(x)
ammetta derivata prima continua sia su (a,x0)
che su (x0,b)
e che esistano finiti i limiti
lim x→x0−f′(x), lim
x→x0+f′(x).
In questo caso la serie di Fourier di f(x)
converge in ogni punto di (a,b)
e inoltre:
- Se [a′,b′] ⊆ (a,x
0)
oppure se [a′,b′] ⊆ (x
0,b)
allora la serie converge uniformemente ad f(x)
su [a′,b′].
- in x0
la serie di Fourier converge alla media dei valori dei limiti direzionali in
x0:
1
2 f(x0−) + f(x0+) .
Esempio 96 Sia
χ(x) = − 1se − π < x < 0 5 se x = 0
1 se 0 < x < π.
Si noti che questa funzione differisce dalla funzione sgn(x)
per il valore che assume in 0;
ma il valore assunto in un solo punto non altera gli integrali che definiscono i
coeffcienti di Fourier. Dunque le funzioni definite su [−π,π]
ed uguali a χ(x)
ed a sgn(x)
hanno la medesima serie di Fourier, che è la serie
4
π sin x
1 + sin 3x
3 + sin 5x
5 + ⋯
Per x = 0
questa serie converge e converge al valore 0,
media dei limiti direzionali di χ(x)
per x →±0.
Per il teorema 95 la somma della serie è quindi sgn(x).
La convergenza non può essere uniforme perché le somme parziali sono
continue mentre la somma della serie non è continua. Se si disegnano alcune
somme parziali, come in figura 2.10, si vede che le somme parziali saltano sopra
e sotto il valore ±1
di una quantità che non si attenua al crescere di N.
Calcoli piuttosto laboriosi mostrano che
lim N→+∞SN(1∕N) = d
e si può mostrare che d
è strettamente maggiore di 1:
d > 1, 089.
E quindi al crescere di N
l’errore tra SN(x)
e sgn(x)
non si attenua (ma si concentra sempre di più intorno al salto
x = 0). _
Il fenomeno appena illustrato non dipende dalla particolare funzione
sgn(x)
usata nell’esempio. Si può provare che, nelle ipotesi del Teorema 95, esso
si verifica in vicinanza di ogni salto. Tale fenomeno va sotto il nome di
Fenomeno di Gibbs. Infine, riportiamo alcune serie di Fourier di funzioni
f(x) periodiche
di periodo 2π
e, nelle figure seguenti, i grafici della restrizione della funzione a
(−π,π),
con sovrapposti i grafici di alcune somme parziali. Nella colonna
di sinistra della tabella, si riporta l’espressione della funzione su
(−π,π). La funzione è
poi estesa ad ℝ
per periodicità.
signx
4
π sin x
1 + sin3x
3 + sin 5x
5 + ⋯
|x|
π 2 − 4 π ( cos x 1 2 + cos 3 x 3 2 + c o s 5 x 5 2 + ⋯ )
x
2 ( sin x 1 − sin 2 x 2 + sin 3 x 3 − ⋯ ) .
{ x + 2 π s e − π < x < 0 x s e 0 < x < π
π − 2 ( sin x 1 + sin 2 x 2 + sin 3 x 3 + ⋯ )
| sin x |
2 π − 4 π ( cos 2 x 1 ⋅ 3 + cos 4 x 3 ⋅ 5 + cos 6 x 5 ⋅ 7 + ⋯ ) .
s g n ( x ) cos x
8 π ( sin 2 x 1 ⋅ 3 + 2 sin 4 x 3 ⋅ 5 + 3 sin 6 x 5 ⋅ 7 )
Capitolo 3
Lo spazio lineare normato
ℝn
In questo capitolo richiamiamo e precisiamo alcuni concetti che dovrebbero essere
noti dai corsi precedenti, in particolare dal corso di Geometria. Tratteremo
- lo spazio lineare ℝn.
- introdurremo “norme” e “distanze” in ℝn,
che permetteranno di definire i punti di accumulazione, gli insiemi aperti
e gli insiemi chiusi. Ciò fatto sarà possibile studiare limiti continuità
e derivabilità.
- introdurremo quindi il concetto di “insieme convesso” e di “insieme
connesso”.
- richiameremo le trasformazioni di coordinate in ℝn
e la loro relazione con l’orientazione dello spazio.
- introdurremo altri modi (altri “sistemi di coordinate”) per rappresentare
i punti di ℝ2
e di ℝ3.
- studieremo le funzioni da ℝ
in ℝn.
I casi su cui insisteremo di più saranno i casi
n = 2 ed
n = 3.
3.1 Lo spazio lineare ℝn
Non intendiamo qui richiamare la definizione astratta di spazio lineare, vista nei corsi
di Geometria. Ci limitiamo a richiamare le sole nozioni necessarie per lo studio di
ℝn. Gli
elementi di ℝn
sono le n-ple
ordinate di numeri reali che chiameremo indifferentemente “punti”
o “vettori”. E’ bene essere precisi con la notazione. Una di tali
n-ple
si potrà scrivere come una sequenza ordinata di
n numeri
reali x1,
x2,
⋯,
xn
scritta in orizzontale o in verticale, ossia come
x1x2x3⋯xn oppure x1
x2
x3
⋮ x
n .
Noi useremo sempre la rappresentazione in verticale. Però, talvolta
sarà conveniente scrivere in orizzontale, con un apice (segno di trasposizione).
Ossia intendiamo
x1x2x3⋯xn ′ = x1
x2
x3
⋮ x
n .
Notiamo inoltre che la definizione di ℝn
è suggerita dalla rappresentazione del piano in coordinate cartesiane. Quando
n = 2 oppure
n = 3, per indicare
il punto x1x2x3 ′
useremo anche la notazione dellla geometria analitica,
P(x1,x2,x3). Gli
elementi di ℝn,
ossia i “vettori”, si indicheranno con una lettera in grassetto:
x→ = x1
x2
x3
⋮ x
n .
Ricordiamo che nei corsi di fisica i vettori si indicano con
lettere in grassetto oppure con una freccia sovrapposta,
x→; talvolta con una lettera
maiuscola, X, oppure con
una lettera sottolineata, x̲.
I numeri xi si chiamano le
componenti del vettore x→.
Il vettore le cui componenti sono tutte nulle si chiama vettore nullo e si indica col simbolo
0 → (da non confondere
col simbolo 0 usato per
l’elemento nullo di ℝ). In
geometria analitica, il punto 0 →
si chiama anche origine delle coordinate e si indica col simbolo
O, iniziale di “origine”.
Di regola, se x→
indica un vettore, le sue componenti si indicheranno come
xi.
Ricordiamo che spesso i vettori si indicano col simbolo
v→, iniziale di “vettore”,
ma anche col simbolo r→,
iniziale di “raggio vettore”. Questo per quanto riguarda le notazioni con cui si indicano gli
elementi di ℝn.
Lo spazio ℝn
però non è solo un isieme di elementi, ma è anche uno
spazio vettoriale.
Infatti gli elementi di ℝn
si possono moltiplicare per numeri reali (che si chiamano anche scalari) e si possono sommare
tra loro. Se α
è un numero reale, per definizione si ha
α x1
x2
x3
⋮ x
n = αx1
αx2
αx3
⋮ αx
n .
La somma dei vettori x→
e y→
si ottiene sommando le componenti corrispondenti:
x→ = x1x2x3⋯xn ′,
y→ = y1y2y3⋯yn ′, la
loro somma è
x→+y→ = x1
x2
x3
⋮ x
n + y1
y2
y3
⋮ y
n = x1 + y1
x2 + y2
x3 + y3
⋮ x
n + yn .
Si rinvia ai corsi di Geometria per le proprietà di queste operazioni. Ricordiamo però
che se n = 3
l’operazione di somma appena definita corrisponde alla somma di vettori con la regola
del parallelogramma nota dai corsi di fisica. Come terminologia, diremo anche che
x→ + y→ è ottenuto
traslando di x→
il vettore y→
o, in modo equivalente che è ottenuto traslando di
y→ il vettore
x→. Si considerino
ora r
vettori v→1,
…, v→r di
ℝn. Il
vettore
∑
i=1rα
iv→i
(con αi
numeri reali) si chiama combinazione lineare dei vettori
v→i.
L’insieme delle combinazioni lineari si chiama s.spazio lineare generato dai vettori
v→1, …,
v→r di
ℝn. Esso contiene sempre
0 →, che si ottiene scegliendo
nulli tutti gli αi. Si potrebbe
trovare 0 → anche con altre
scelte degli αi. Se ciò
non accade, i vettori v→i
si chiamano linearmente indipendenti Ossia, i vettori
v→i sono
linearmente indipendenti quando
∑
i=1rα
iv→i = 0 →
implica αi = 0 per tutti gli indici
i. In questo caso l’insieme
dei vettori v→i si chiama
una base del s.spazio. Se r = n
e se i vettori v→i
sono linearmente indipendenti, lo spazio da essi generato è
ℝn e si dice che i
vettori v→i sono
una base di ℝn.
Osserviamo che ogni s.spazio lineare è esso stesso uno spazio lineare
rispetto alle operazioni di somma e di prodotto per scalari. Come base di
ℝn si potranno
scegliere n
vettori indipendenti qualsiasi. Scegliendo però i vettori
e→k,
e→k = 0 0
⋮ 1
⋮ 0
con 1 nella
posizione k
e gli altri elementi tutti nulli, si ha la base canonica.
Esempio 97 Si sa dalla geometria analitica che i s.spazi di ℝ2
sono 0 →,
ℝ2
e le rette per l’origine. Se invece n = 3
i s.spazi sono 0 →,
ℝ3,
le rette per l’origine ed i piani per l’origine. _
Siano ora X ed
Y due s.insiemi
di ℝn. Col
simbolo X + Y
si intende l’insieme
X + Y = {x→ + y→,x→ ∈ X,y→ ∈Y }.
A noi interessa in particolare il caso in cui
Y è un s.spazio
mentre X ha
l’unico elemento x→0.
L’insieme X + Y
in questo caso si indica col simbolo
x→0 + Y
e si chiama s.spazio affne di ℝn,
parallelo ad Y ,
ottenuto traslando Y
di x→0 o anche
in x→0. Si
noti che:
- Se x→0∉Y
allora 0 →∉x→0 + Y .
- in generale, un s.spazio affne non è un s.spazio lineare. Lo è se e solo se
si ha x→0 + Y = Y
e ciò avviene se e solo se x→0 ∈ Y ;
Come terminologia, in generale chiameremo semplicemente “s.spazi” i s.spazi lineari
mentre l’aggettivo “affne” non verrà mai omesso, salvo nei casi particolari
seguenti, nei quali useremo i termini “retta” e “piano” propri della geometria:
- Gli spazi della forma {ty→0}t∈ℝ
(con y→0≠0)
si chiamano rette per l’origine e x→0 + ty→0,
t ∈ ℝ,
si chiama retta per x→0
parallela ad y→0
(che deve essere non nullo).
- si chiama piano per l’origine in ℝn
l’insieme dei punti x→
le cui componenti x1,
…,xn
verificano l’equazione lineare
a1x1 + a2x2 + ⋅ + anxn = 0.
I parametri a1,
…an
sono fissati, non tutti nulli. Se X
è un piano per l’origine ed y→ = y1…yn ′
un punto fissato di ℝn,
l’insieme y→ + X
si chiama piano per y→
e si vede facilmente che le componenti dei suoi punti verificano
a1(x1 − y1) + a2(x2 − y2) + ⋅ + an(xn − yn) = 0.
Vettori colineari e rette parallele
Due vettori non nulli v→
e w→ si
dicono colineari quando le componenti corrispondenti sono proporzionali, ossia quando
esiste α ∈ ℝ,
α≠0, tale
che
v→ = αw→.
Col linguaggio della geometria analitica, i due vettori
v→ e
w→ sono
colineari quando identificano la medesima retta uscente dall’origine. Consideriamo ora
due rette,
|
x→0 + tv→,t ∈ ℝ , y→0 + τw→,τ ∈ ℝ .
| (3.1) |
Le due rette si dicono parallele quando i due vettori
v→ e
w→
sono colineari. Geometricamente questo significa che un punto
Q della seconda retta si
ottiene da un punto P
della prima retta, traslandolo mediante il vettore
y→0 −x→0, indipendente
dai punti P
e Q
considerati. Due rette non parallele possono avere un punto comune,
o meno. Nel secondo caso le rette si dicono sghembe Se le due rette
hanno un punto comune, si dicono incidenti Ciò accade quando esistono
t e
τ tali
che
x→0 + tv→ = y→0 + τw→ossiax→0 −y→0 = τw→ − tv→.
Dunque, le due rette (3.1) sono incidenti se e solo se
x→0 −y→0 appartiene al
piano generato da v→
e w→.
Osservazione 98 Sia m≠0.
Le due rette
x→0 + ty→0,x→0 + tmy→0,t ∈ ℝ
coincidono. _
3.1.1 Connessione e convessità
I punti di una retta hanno rappresentazione
Il punto x→0 si
ritrova scegliendo t = 0.
Per questo, come si è detto, questa retta si chiama “retta per
x→0, parallela
ad y→0”. Sia ora
x→1 un secondo punto di
ℝn. Chiediamoci se, per qualche
selta di y→, la retta (3.2) contenga
x→1 ossia, come si dice, “passi
anche per x→1”. Ciò avviene
quando per un certo valore t1
del “parametro” t
si ha
x→0 + t1y→ = x→1.
Questo è un insieme di n
equazioni nelle n componenti
di y→. L’uguaglianza si
ottiene solo quando y→
è dato da
y→ = 1
t1 x→1 −x→0 .
Il valore t1
può scegliersi arbitrariamente, purché non
nullo. Dunque,
scelto t1 = 1, la
retta per x→0
e x→1 si
rappresenta come
x→ = x→0 + t x→1 −x→0 .
Il suo s.insieme
x→0 + t x→1 −x→0 ,t ∈ [0, 1]
si chiama segmento congiungente x→0
ed x→1. I
punti x→0
ed x→1
si chiamano gli estremi del segmento. Precisamente,
x→0, ottenuto per
t = 0, si chiama il “primo
estremo” ed x→1, ottenuto
per t = 1, si chiama il
“secondo estremo”.
Se x→0 = x→1, il segmento
degenera nel punto x→0:
x→0 = x→0 + t x→1 −x→0 = x→0 + t x→0 −x→0
per ogni t.
Definiamo ora cosa si intende per “spezzata” di
ℝn.
Questo termine indica un numero finito di segmenti che “si susseguono”;
ossia tali che il secondo estremo di uno sia anche primo estremo
del successivo; ossia, consideriamo un numero finito di segmenti
I1,
I2, …,
Ik. Se accade che per
1 < j < k il primo estremo di
Ij+1 coincide col secondo
estremo di Ij, l’insieme
∪j=1kI
j si dice una spezzata. Si
dice che una spezzata ∪j=1kI
j
congiunge i due punti x→
ed y→ quando
x→ è il primo
estremo di I1 e
y→ è il secondo
estremo di Ik.
Se accade che tali due punti coincidono, la spezzata si dice chiusa. Sia ora
A un s.insieme
di ℝn. L’insieme
A si dice
connesso quando ogni
coppia di punti di A
può essere congiunta con una spezzata i cui punti appartengono ad
A. Inoltre,
si considerano connessi anche gli insiemi costituiti da un solo punto. Un insieme che è
sia aperto che connesso si chiama un dominio Può accadere che l’insieme connesso
A contenga un punto
x→0 con questa proprietà: ogni
altro punto x→1 ∈ A può essere
congiunto ad x→0 mediante
un segmento contenuto in A;
ossia mediante una spezzata costituita da un unico segmento. In tal caso l’insieme
A si dice stellato
rispetto ad x→0.
Sia ora C un
s.insieme di ℝn.
Si dice che C
è convesso
- quando è vuoto oppure contiene un solo punto
- oppure quando contiene il segmento congiungente due qualsiasi dei suoi
punti.
Ossia, se a
C
appartengono almeno due punti, allora
C
è convesso quando è stellato rispetto a ciascuno dei suoi punti. La figura 3.1
rappresenta un insieme connesso, a sinistra, ed un insieme convesso, a destra.
Per n = 1
le tre definizioni di insieme connesso per archi, stellato e convesso si riducono a
quella di intervallo.
3.1.2 Vettori liberi e vettori applicati
L’uso dei vettori è suggerito dalle applicazioni fisiche: un “vettore” può
rappresentare, per esempio, una forza o uno spostamento. Domanda
ovvia: spostamento da dove, o forza applicata dove? I vettori come
n-ple
ordinate di numeri reali non permettono di rispondere a queste domande. Tali
vettori possono usarsi per rappresentare uno “spostamento” nel senso della distanza
percorsa, in una certa direzione e in un certo verso, indipendentemente da quale sia
il punto di partenza; o una forza di una certa intensità diretta secondo una certa
direzione e con un certo verso, indipendentemente da dove essa sia applicata. Per
questa ragione, i vettori che abbiamo introdotto si chiamano in fisica vettori liberi
Si può decidere di applicare tutti i vettori liberi in un punto convenzionalmente
scelto. La scelta naturale è di applicarli nell’origine: i vettori liberi verranno
interpretati anche come vettori applicati nell’origine e quindi, per esempio, il vettore
135 ′rappresenta lo spostamento,
in linea retta, da O
al punto P(1, 3, 5).
Se vogliamo rappresentare un vettore applicato dobbiamo dare una coppia di
vettori: il primo rappresenta il punto di applicazione e il secondo rappresenta il
vettore (forza, spostamento,…) in esso applicato. A noi non serve essere troppo
formali a questo proposito, ma è necessario sapere che:
- sui vettori applicati nel medesimo punto si fanno tutte le operazioni (sia
quelle già introdotte che quelle che introdurremo) che possono farsi tra
vettori liberi. Dunque, se 123 ′
e 456 ′
rappresentano due vettori applicati nel medesimo punto, per esempio nel
punto P(4, 4, 4),
la loro somma è il vettore 579 ′
ancora applicato in P(4, 4, 4).
- Non si fanno operazioni tra vettori applicati in punti diversi.
- Un vettore v→
applicato in P
può spostarsi per parallelismo in un vettore applicato in Q
procedendo come segue: al vettore v→
applicato in P
si fa corrispondere il vettore v→
applicato in Q.
- Se si vogliono fare operazioni tra vettori applicati in punti diversi,
bisogna prima di tutto traslarli per parallelismo, applicandoli in un punto
comune.
3.2 Basi e basi ordinate
Ricordiamo che una base di ℝn
è un insieme di n
vettori linearmente indipendenti. Un insieme non cambia se si
cambia l’ordine col quale se ne elencano gli elementi. Se però
B è
un insieme finito e si stabilisce un ordine tra i suoi elementi, si dice che
B è un insieme
ordinato e se B
è una base di ℝn,
si dice che B
è una base ordinata. Per esempio, se si stabilisce di elencare gli elementi della base canonica
elencando ej
al j–mo posto
si ha una base ordinata, ma si ha una base ordinata anche se si stabilisce di elencarne gli
elementi a rovescio, oppure prima quelli di indice pari e poi quelli di indice dispari. Quando in
ℝn si è stabilita una
base ordinata si possono fare cose che non sono possibili con basi non ordinate. Per esempio, sia
𝒜 è una trasformazione
lineare da ℝn
in ℝm e siano
rispettivamente {e→i} ed
{→ẽj} due basi ordinate
la prima di ℝn e la
seconda di ℝm. La
trasformazione 𝒜
si può rappresentare con una matrice come segue. Si considera l’elemento
𝒜e→1 ∈ ℝm.
Questo si rappresenta come
𝒜e→1 = ∑
j=1ma
1j →ẽ
j.
Si costruisce una matrice mettendo il numero
a1j nella
posizione j
della prima colonna. La seconda colonna si costruisce in modo analogo a partire da
𝒜e→2 e così via fino
a costruire l’n-ma
colonna. Si costruisce così una matrice
A che rappresenta la
trasformazione lineare 𝒜.
Se la base prescelta è quella canonica e se non si stabilisce diversamente in modo
esplicito, si intende che la base canonica è una base ordinata e che gli elementi della
base si susseguono nell’ordine dei loro indici:
e→1,e→2,…,e→n.
Si dice che una base ordinata subordina un’orientazione di
ℝn. Visto che
una base di ℝn
contiene n
elementi, ci sono n!
modi di elencarli e quindi si potrebbe pensare che in
ℝn ci siano
(almeno) n!
orientazioni diverse. Invece non è così. Consideriamo per questo una base ordinata
B1 ed una seconda
base ordinata B2,
(che potrebbe essere ottenuta dagli stessi elementi di
B1,
ordinati in modo diverso). Si sa dal corso di Geometria che i cambiamenti
di base si rappresentano mediante una matrice invertibile. Sia
P
la matrice che trasforma ordinatamente gli elementi di
B1 in quelli
di B2.
Essendo P
invertibile, il suo determinante non è zero e quindi delle due l’una:
det P > 0oppure det P < 0.
Se det P > 0 si dice che
le due basi B1 e
B2 subordinano la medesima
orientazione di ℝn,
altrimenti subordinano orientazioni opposte. Dunque, in
ℝn si
trovano due orientazioni, che si dicono opposte l’una dell’altra.
3.2.1 Il piano e lo spazio
I punti del piano si mettono in corrispondenza biunivoca con quelli di
ℝ2
procedendo come segue: si fissano due rette incidenti (e tra loro diverse)
r ed
s del piano ed un’unità di
misura per le lunghezze.
Il punto comune alle due rette si chiama origine. Su ciascuna delle
due rette si fissa un verso (che si chiama “positivo”). Il segmento
PO della
retta r
ha lunghezza positiva quando un punto che parte da
O incontra
P
muovendosi nel verso positivo; negativo altrimenti. In tal caso si dice che
P
appartiene al semiasse positivo. La stessa convenzione si usa sulla retta
s. Si
fissa quindi un ordine tra le due rette. La prima si chiama asse delle ascisse o asse
x e la seconda asse
delle ordinate o asse y
Le due rette si chiamano assi coordinati Le rette del piano parallele agli assi coordinati
si chiamano rette coordinate Facendo ciò, si dice che si è definita un’orientazione
del piano. Si fa quindi corrispondere l’orientazione del piano con quella di
ℝ2 associando il vettore
e→1 al punto dell’asse delle
ascisse a distanza +1
dall’origine e il vettore e→2
col punto dell’asse delle ordinate a distanza
+1 dall’origine. Sia
P un punto del piano. Si
fanno passare per P due
rette r1, parallela all’asse
delle ordinate, ed r2 parallela
a quella delle ascisse. Sia P1
il punto in cui r1 incontra
l’asse delle ascisse e P2
l’intersezione di di r2 con
quello delle ordinate. Siano x
ed y le lunghezze, con
segno, rispettivamente di OP1
e di OP2. Al
punto P
si fa corrispondere il vettore
x→ = xe→1 + ye→2.
Viceversa, ad ogni vettore x→
si fa corrispondere un punto del piano. Si noti che perchè ciò abbia senso, va
stabilito prima quale asse scegliere come asse delle ascisse, e quale dei due elementi
della base considerare per primo. Ossia, la corrispondenza biunivoca che
abbiamo costruito è tra il piano, a cui abbiamo imposto un’orientazione, ed
ℝ2, a cui
abbiamo imposto un’orientazione. In pratica, si segue questa convenzione:
- La base canonica di ℝ2
si ordina scegliendo prima e→1;
- sia fissato l’asse delle ascisse e il verso su di esso. Il semiasse “positivo”
delle ascisse si può sovrapporre ad uno dei semiassi delle ordinate con
due rotazioni una oraria ed una antioraria. Dei due angoli, uno è minore
dell’altro. L’orientazione positiva sull’asse delle ordinate si sceglie in
modo che la sovrapposizione avvenga girando l’asse delle ascisse in verso
antiorario e dell’angolo minore.
La figura 3.2 illustra la situazione.
Il più delle volte gli assi coordinati si prendono ortogonali tra loro e
l’asse delle ascisse si rappresenta orizzontale, col verso positivo verso destra.
In tal caso il verso positivo dell’asse delle ordinate punta verso l’alto. La
rappresentazione dello spazio è analoga. Senza entrare nei dettagli, consideriamo
subito il caso di un sistema cartesiano ortogonale. Si scelgono tre rette
tra loro ortogonali che si chiamano rispettivamente delle ascisse o asse
x, delle ordinate
o asse y, delle
quote o asse z
Gli assi x ed
y identificano un
piano, il piano (x,y), a cui
l’asse z è ortogonale.
L’orientazione sul piano (x,y)
si fissa come si è detto sopra. Rimane quindi da scegliere il verso positivo dell’asse
z.
Questo si sceglie in modo che un osservatore in piedi sul piano
(x,y), appoggiato
all’asse z
e con la testa nel verso positivo veda che il semiasse
x positivo si riporta
sul semiasse y
positivo ruotandolo dell’angolo minore e in verso antiorario. Consideriamo ora il punto
(1, 0, 0). Ruotando l’asse
delle ascisse di un’angolo giro, esso descrive una circonferenza e, se l’orientazione del piano
(x,y) è positiva,
raggiunge il punto (0, 1, 0)
dopo una rotazione di un angolo retto in verso antiorario. Un insetto che parta da
(1, 0, 0)
e si muova lungo la circonferenza verso il punto
(0, 1, 0), raggiungendolo
dopo la rotazione di π∕2,
vede il disco alla sua sinistra. E’ questa la prima comparsa della regola
d’Ampère per la determinazione dell’orientazione dello spazio. Ogni punto
P si rappresenta mediante
le sue tre coordinate x,
y e
z. Queste si ottengono
facendo passare per P
tre piani, paralleli ai piani individuati dalle coppie di assi coordinati (che si chiamano piani
coordinati). L’ascissa x
di P è
la distanza dall’origine dell’intersezione tra l’asse delle ascisse e il piano per
P paralello
agli assi y
e z,
presa con segno. L’ordinata e la quota si definiscono in modo analogo. Si chiamano
rette coordinate le rette dello spazio parallele agli assi cartesiani. Sia ora
P un punto (del piano o
dello spazio), P(x,y,x). Facciamogli
corrispondere il vettore v→ = xe→1 + ye→2 + ze→3
che si interpreta come “spostamento” percorso da un punto
che partendo dall’origine raggiunge la posizione occupata da
P.
In questo modo, lo spazio si mette in corrispondenza biunivoca con
ℝ3, che
si pensa orientato mediante la sua base canonica. Quando si lavora con un
sistema di assi cartesiani ortogonali, si usano i simboli sequenti: lavorando sul
piano,
i→ = e→1 = 1 0 ,j→ = e→2 = 0 1 .
Invece lavorando nello spazio
i→ = e→1 = 1 0
0 ,j→ = e→2 = 0 1
0 ,k→ = e→3 = 0 0
1 .
3.3 Norme e distanze
La teoria dei limiti per le funzioni di una variabile dipende in modo essenziale dalle
proprietà seguenti del valore assoluto:
- Per ogni x
reale, |x|≥ 0
e |x| = 0
se e solo se x = 0;
- Il valore assoluto di un prodotto è il prodotto dei valori assoluti: |xy| = |x|⋅|y|;
- la disuguaglianza triangolare: |x + y|≤|x| + |y|.
Ricordiamo che da queste proprietà segue anche:
||x|−|y|| ≤|x − y|.
Esaminando il corso di Analisi Matematica 1, si vede facilmente che queste sono le
uniche proprietà che servono per la teoria dei limiti, eccezion fatta per quei
teoremi che richiedono una relazione di ordine, come i teoremi del confronto o delle
funzioni monotone. L’osservazione precedente suggerisce di definire norma su
ℝn una funzione
definita su ℝn
ed a valori reali, con le proprietà che ora descriviamo. Una norma si indica col
simbolo ∥⋅∥.
Con questo simbolo, le proprietà sono:
- la norma prende valori non negativi: ∥x→∥≥ 0
per ogni x→;
- la norma si annulla solo in 0 →:
∥x→∥ = 0
implica x→ = 0 →;
- vale ∥tx→∥ = |t|⋅∥x→∥
per ogni x→
e per ogni numero reale t.
Si noti che scegliendo t = 0
si trova ∥0 →∥ = 0.
- vale la disuguaglianza triangolare: per ogni coppia di vettori x→
e y→
si ha:
∥x→ + y→∥≤∥x→∥ + ∥y→∥.
Non è diffcile provare:
Lemma 99 Per ogni x→,
y→
vale
|∥x→∥−∥y→∥| ≤∥x→ −y→∥.
Dim. Esattamente come nel caso dei numeri, si nota che la disuguaglianza da provare
equivale alle due disuguaglianze
−∥x→ −y→∥≤∥x→∥−∥y→∥≤∥x→ −y→∥.
La seconda disuguaglianza segue dalla disuguaglianza triangolare, scrivendo
∥x→∥ = ∥x→ −y→ + y→∥≤∥x→ −y→∥ + ∥y→∥.
L’altra segue in modo analogo, scrivendo
∥y→∥ = ∥y→ −x→ + x→∥≤∥y→ −x→∥ + ∥x→∥ = ∥x→ −y→∥ + ∥x→∥.
Dunque, definita una norma, è possibile trattare la teoria dei limiti su
ℝn esattamente
come per n = 1,
provando tutti i medesimi teoremi, con le stesse dimostrazioni, a parte
quelli che fanno intervenire la monotonia. Mostriamo che norme su
ℝn
esistono:
Esempio 100 Le seguenti sono norme su ℝ2:
xy ′
1 = |x|+|y|, xy ′
∞ = max{|x|,|y|}.
Si mostri per esercizio che le due funzioni definite sopra effettivamente
soddisfano alle proprietà richieste per la definizione di norma. _
Quindi, su ℝ2
possono definirsi almeno due norme diverse. In realtà si possono definire infinite
norme diverse. Infatti:
Teorema 101 Sia p ≥ 1
e sia ℝn
rappresentato rispetto alla base canonica. Ciascuna delle seguenti è una norma
su ℝn:
∥x→∥p = ∑
i=1n|x
i|p 1∕p.
Diciamo subito che la norma di gran lunga più importante è la norma che corrisponde al numero
p = 2, che si chiama
norma euclidea:
∥x→∥2 = |x1 |2 + |x2 |2 + ⋯ + |xn |2.
Introdotta una norma si può introdurre la distanza tra i vettori,
d(x→,y→) = ∥x→ −y→∥
e quindi definire:
Definitione 1 Sia x→0
un punto di ℝn
e sia r > 0.
Si chiama intorno di x→0
di raggio r,
o palla aperta di centro x→0
e raggio r
l’insieme
B(x→0,r) = {v→|∥x→0 −v→∥ < r}.
Dato un insieme A
di ℝn ed un
vettore x→0,
si dice che:
- Un insieme è limitato quando esiste una palla che lo contiene.
- x→0
è interno ad A
se esiste r > 0
tale che B(x→0,r) ⊆ A;
- Si dice che x→0
è punto di accumulazione per A
se per ogni r > 0
esiste a→ ∈ A,
a→≠x→0,
con a→ ∈ B(x→0,r).
- Il punto x0
è punto della frontiera di A
se non è interno né ad A
né al suo complementare.
- Un insieme si dice aperto se tutti i suoi punti sono interni, oppure se è
vuoto; chiuso se contiene tutti i suoi punti di accumulazione oppure se
è vuoto. Si mostra facilmente che un insieme è aperto se e solo se il
suo complementare è chiuso.
- Si chiama successione a valori in ℝn
una funzione che ad ogni numero naturale associa un vettore di ℝn.
- Una successione è limitata quando limitata è la sua immagine.
- Sia {v→n}
una successione. Si dice che
lim nv→n = v→0
quando, per ogni 𝜖 > 0
esiste N𝜖
tale che se n > N𝜖
si ha v→n ∈ B(v→0,𝜖).
Dato che le norme su ℝn
sono infinite, potrebbe sembrare che ci siano infinite teorie dei limiti
tra loro diverse. Invece, fortunatamente, le proprietà di avere o non
avere limite, il valore dell’evenuale limite e le proprietà dei limiti
non dipendono dalla definizione di norma che si decide di usare in
ℝn.
Prima di provare questo fatto, illustriamone
la ragione intuitiva consideriamo le tre norme
∥⋅∥1,
∥⋅∥2
e ∥⋅∥∞
in ℝ2.
La figura 3.3 mostra le palle di centro
0
e raggio 1
relative alle tre norme. La palla relativa alla norma euclidea è un
disco, in figura rappresentata come un ellisse perché l’unità di
misura sui due assi non è la medesima. Le altre due palle sono
quadrati (rettangoli in figura, per la ragione detta sopra). Quello
con i lati paralleli agli assi coordinati è la palla nella norma
∥⋅∥∞.
Si vede da questa figura che se una successione
v→n
tende a zero rispetto ad una di queste norme, entra e rimane definitivamente
dentro ciascuna delle tre palle; e quindi tende a zero anche rispetto alle altre
norme.
Il risultato generale è conseguenza delle disuguaglianze seguenti. La prima è
ovvia mentre omettiamo la dimostrazione della seconda.
Lemma 102 Sia ∥⋅∥p,
1 ≤ p ≤ +∞ una
norma di ℝn.
Valgono le due disuguaglianze seguenti:
- Per ogni i
vale |xi|≤∥x→∥;
- Esiste un numero M
(che dipende da n
e da p)
tale che ∥x→∥p ≤ M∑
i−1n|x
i| = ∥x→∥1.
In definitiva, per 1 ≤ p ≤ +∞
si ha
|
∥x→∥1 ≤ n∥x→∥p ≤ Mn∥x→∥1.
| (3.3) |
Accettando questo lemma possiamo provare:
Teorema 103 In ℝn,
una successione (v→n)
converge a v→0
in norma p
se e solo se converge al medesimo limite v→0
in qualsiasi altra norma q.
Si ha ∥v→n∥p → +∞
se e solo se ∥v→n∥q → +∞.
Dim. Proviamo il primo asserto. Sostituendo
v→n con
v→n −v→0
si può studiare il caso della convergenza a zero. Proviamo che
∥v→n∥p → 0 se e solo
se ∥v→n∥1 → 0. Questo
è immediato dal teorema del confronto per i limiti (di successioni a valori reali)
applicato alla disuguaglianza (3.3). Il secondo asserto si prova in modo ovvio. _ Inoltre,
sia (vni)
la successione di numeri reali ottenuta considerando la componente
i-ma dei
vettori v→n.
Le disuguaglianze (3.3) mostrano:
Teorema 104 La successione (v→n)
converge se e solo se ciascuna delle successioni di numeri reali (vni)
è convergente e il vettore lim v→n
ha per i-ma componente il numero lim vni.
Osservazione 105 Si noti che un asserto analogo non vale per successioni
divergenti ossia tali che
lim ∥v→n∥ = +∞.
Per questo basta che una delle successioni
(vni)
diverga! _
3.3.1 Completezza di ℝn
Si chiama successione fondamentale o successione di Cauchy una successione
(v→n) con
questa proprietà:
Per ogni 𝜖 > 0
esiste N𝜖
tale che se n > N𝜖,
m > N𝜖
allora
∥v→n −v→m∥ < 𝜖.
In simboli,
∀𝜖 > 0∃N𝜖|n > N𝜖,m > N𝜖⇒∥v→n −v→m∥ < 𝜖.
Una dimostrazione analoga a quella del Teorema 103 mostra che la proprietà di
essere fondamentale non dipende dalla norma usata e per questo nella
definizione precedente abbiamo usato il generico simbolo di norma. Inoltre le
disuguaglianze (3.3) mostrano che:
Teorema 106 La successione
(v→n)
è fondamentale se e solo se ciascuna delle sue componenti è una successione
fondamentale di numeri reali.
Si sa dal corso di Analisi Matematica 1 che una successione di numeri converge
se e solo se è fondamentale. E quindi quest’asserto vale anche in
ℝn:
Teorema 107 Una successione
(v→n)
di
ℝn
converge se e solo se è fondamentale.
Per dire che in ℝn
le successioni convergenti sono tutte e sole le successioni fondamentali si dice che
ℝn è completo
Una successione (v→n)
si dice limitata la sua immagine è limitata, ossia quando esiste
M tale
che
per ogni n vale ∥v→n∥ < M.
Le disuguaglianze (3.3) mostrano che una successione è limitata se e
solo se sono limitate le successioni delle sue componenti; e quindi anche in
ℝn vale il
Teorema di Bolzano-Weierstrass:
Teorema 108 (di Bolzano-Weierstrass) Ogni successione limitata
ammette s.successioni convergenti.
3.4 La norma euclidea
La norma di gran lunga più utile è la norma
∥⋅∥2, perché
essa ha una proprietà ben particolare, che ora illustriamo. Dai corsi di Geometria
si sa che è possibile definire il prodotto scalare, detto anche prodotto interno, in
ℝn e
che quando si conoscono le componenti di due vettori rispetto alla base
canonica
x→ = ∑
i=1nα
ie→i,y→ = ∑
i=1nβ
ie→i.
il prodotto scalare si calcola come
x→ ⋅y→ = ∑
i=1nα
iβi.
Si vede quindi che:
Osservazione 109 Si osservi che il prodotto scalare di vettori associa a due
vettori un numero (e non un vettore)! _
Diciamo infine che un vettore che ha norma euclidea uguale ad
1 si chiama versore I
particolari versori i→,
j→,
k→ di
ℝ3 (o di
ℝ2 se non si
considera k→)
si chiamano i versori degli assi coordinati. Chiamiamo ora ortogonali due vettori che
hanno prodotto scalare nullo e mostriamo che vale:
Teorema 110 (Teorema di Pitagora) Se x→
e y→
sono due vettori di ℝn,
si ha
∥x→ + y→∥22 = ∥x→∥
22 + ∥y→∥
22.
Dim. Si ricordi dai corsi di geometria che il prodotto scalare gode della
proprietà distributiva:
x→ ⋅ (y→ + z→) = x→ ⋅y→ + x→ ⋅z→ = (y→ + z→) ⋅x→.
Dunque,
|
∥x→ + y→∥22 = (x→ + y→) ⋅ (x→ + y→)
= x→ ⋅x→ + (x→ ⋅y→ + y→ ⋅x→) + y→ ⋅y→ = ∥x→∥22 + |y→∥
22
|
perché ambedue gli addendi in parentesi sono nulli. _
Quando x→
e y→
sono ortogonali, il vettore x→ + y→
è l’ipotenusa del triangolo rettangolo di cateti
x→
e y→,
si veda la figura 3.4. Dunque Il Teorema
di Pitagora si interpetra dicendo che in
ℝ2
il quadrato costruito sull’ipotenusa di un triangolo rettangolo ha per area la
somma delle aree dei quadrati costruiti sui cateti.
Mostriamo ora una particolarissima proprietà della norma euclidea, che si
chiama identità del parallelogramma
Teorema 111 Siano x→
e y→
due vettori di ℝn.
Vale
∥x→ + y→∥2 + ∥x→ −y→∥2 = 2 ∥x→∥2 + ∥y→∥2 .
Dim. Usando la proprietà distributiva del prodotto scalare, calcoliamo
|
∥x→ + y→∥2 + |x→ −y→∥2 = (x→ + y→) ⋅ (x→ + y→) + (x→ −y→) ⋅ (x→ −y→)
= (x→ ⋅x→ + x→ ⋅y→ + y→ ⋅x→ + y→ ⋅y→)
+ (x→ ⋅x→ −x→ ⋅y→ −y→ ⋅x→ + y→ ⋅y→) = 2x→ ⋅x→ + 2y→ ⋅y→ = 2 ∥x→∥2 + ∥y→∥2 .
|
La norma euclidea è l’unica norma che gode di questa proprietà. Per esercizio, si
mostri che la proprietà del parallelogramma non vale per i vettori
01 ′e
10 ′di
ℝ2 con
∥⋅∥∞. La
figura 3.4 a destra mostra il significato dell’identità del parallelogramma in
ℝ2:
x→ + y→ e
x→ −y→
sono le diagonali del parallelogramma identificato dai due vettori
x→ e
y→ e
quindi l’identità del parallelogramma è un’estensione del teorema di Pitagora: in
un parallelogramma, la somma delle aree dei quadrati costruiti sulle due
diagonali è uguale alla somma delle aree dei quadrati costruiti sui quattro lati.
Il prodotto scalare si definisce tra vettori liberi; la definizione si estende
quindi al caso dei vettori applicati nel medesimo punto come si è detto al
paragrafo 3.1.2.
Da ora in poi, se non si specifica esplicitamente il contrario, la norma in
ℝn
sarà la norma |⋅|2,
che indicheremo |⋅|,
sottintendendo l’indice. Useremo norme diverse per fare delle
dimostrazioni se questo sarà conveniente. Infatti, il fatto che la
relazione di convergenza non dipenda dalla particolare norma usata
per verificarla può usarsi per semplificare alcune dimostrazioni.
3.4.1 ℝ2
e ℝ3 con
la norma euclidea
Vogliamo ora esaminare più in dettaglio il caso di
ℝ2 e di
ℝ3 con
norma euclidea. Diamo però la definizione seguente che vale anche in
ℝn,
dotato della norma euclidea e quindi del prodotto interno: due vettori
x→ e
y→ si
dicono ortogonali quando hanno prodotto scalare nullo:
x→ ⊥y→quando x→ ⋅y→ = 0.
Si fissi ora il vettore v→ = ai→ + bj→≠0 →. Sono
ad esso ortogonali i vettori w→1 = bi→ − aj→
e w→2 = −bi→ + aj→.
Le matrici che trasformano la base canonica rispettivamente nella base
{v→,w→1} e
{v→,w→2} sono
rispettivamente
a b b − a , a b − b a .
La prima ha determinante negativo mentre la seconda ha determinante positivo. Dunque,
la base {v→,w→2}è
orientata positivamente, ossia, come anche si dice, ha orientazione concorde con quella dello
spazio. Per questa ragione, se non si specifica esplicitamente il contrario, come vettore
ortogonale a v→
sceglieremo −bi→ + aj→.
Vediamo ora di chiarire il significato geometrico dei determinanti di matrici
2 × 2 e
3 × 3. Siano
v→ e
w→ due vettori, di componenti
rispettivamente (a,b)
e (c,d) rispetto alla
base canonica di ℝ2.
Questi vettori identificano i due punti del piano
P ≡ (a,b) e
Q ≡ (c,d).
Vogliamo calcolare l’area del parallelogramma in figura 3.5. Si sa
che l’area è il prodotto della lunghezza di un lato per l’altezza ad
esso relativa. Scegliendo come lato quello identificato dal vettore
v→ = ai→ + bj→,
vogliamo calcolare
|v→||h→|
ove h→ è il vettore,
applicato in Q,
indicato in figura 3.5.
Dividendo per |v→| non
è restrittivo supporre |v→| = 1,
ossia a2 + b2 = 1. In questo
caso l’area è |h→|.
L’altezza è il vettore
h→ = w→ − (w→ ⋅v→)v→.
Ricordando che a2 + b2 = 1,
si calcola:
|
|h→|2 = w→ − (w→ ⋅v→)v→ ⋅w→ − (w→ ⋅v→)v→
= [c − (ca + bd)a]2 + [d − (ca + bd)b]2
= c2 − 2ac(ca + bd) + d2 − 2bd(ca + bd) + (a2 + b2)(ca + bd)2
= c2(1 − a2) + d2(1 − b2) − 2cabd = (cb)2 + (da)2 − 2cabd
= (cb − ad)2
|
e quindi l’area è
|cb−ad| = det ac b d .
Si trova quindi un’interpretazione geometrica per il valore assoluto del determinante di una
matrice 2 × 2: il
numero det v→w→
è l’area del parallelogramma identificato dai due vettori
v→ e
w→
(applicati nell’origine). Il determinante stesso si interpretra anche come “area con
segno” del parallelogramma identificato dai vettori che sono le colonne della matrice. Si
può quindi concludere che valgono le affermazioni seguenti, per ogni coppia di vettori
v→,
w→ di
ℝ2 (in
quest’ordine) e per la matrice
A = v→w→ :
- Condizione necessaria e suffciente perché i due vettori siano colineari è
che il determinante di A
sia nullo;
- se il determinante è non nullo, i due vettori v→
e w→
(in quest’ordine) sono una base ordinata di ℝ2;
il parallelogramma che essi identificano ha “area con segno” che è
positiva se e solo se essi, presi nell’ordine dato, sono una base orientata
positivamente;
- la matrice A
subordina una trasformazione lineare in
ℝ2. Siano
r→ e
r→′ due vettori (applicati
nell’origine) e r→̃ = Ar→,
r→̃′ = Ar→′ le loro immagini
mediante la matrice A.
Sia R
il parallelogramma identificato dai vettori
r→
e r→′ e
sia R̃
il parallelogramma identificato dalle loro immagini. L’area del parallelogramma
R̃ è il prodotto
di | det A| per l’area del
parallelogramma R:
|
(area di R̃) = det A ⋅(area di R).
| (3.5) |
Risultati del tutto analoghi valgono anche in
ℝ3. Dati tre
vettori u→,
v→ e
w→, in
quest’ordine, si costruisce la matrice
A = u→v→w→ .
Il valore assoluto del suo determinante è il volume del parallelepipedo
identificato dai tre vettori (applicati nell’origine). La matrice
A identifica
una trasformazione lineare. Tale trasformazione applicata ai punti di un parallelepipedo
lo trasforma in un altro, il cui volume differisce da quello del primo per il fattore
| det A|. Il
numero det A
si interpreta come “volume con segno”.
3.5 Il prodotto vettoriale
A differenza delle operazioni tra vettori introdotte fino ad ora, che valgono in
ℝn per
ogni n,
l’operazione di prodotto vettoriale è specifica di
ℝ3. Essa
si definisce ponendo:
i→ ∧i→ = 0, j→ ∧j→ = 0, k→ ∧k→ = 0,
i→ ∧j→ = k→, j→ ∧k→ = i→, k→ ∧i→ = j→,
i→ ∧j→ = −j→ ∧i→,j→ ∧k→ = −k→ ∧j→,k→ ∧i→ = −i→ ∧k→.
Completiamo ora la definizione di prodotto vettoriale ponendo
v→∧w→ = (ai→+bj→+ck→)∧(xi→+yj→+zk→) = (bz−cy)i→+(cx−az)j→+(ay−bx)k→
formalmente ottenuta distribuendo le somme sui prodotti e facendo uso delle regole
per i prodotti vettoriali degli elementi della base. Di conseguenza, si verificano le
regole seguenti:
- v→ ∧w→ = −w→ ∧v→;
- v→ ∧w→
è ortogonale sia a v→
che a w→;
- vale:
(r→∧v→)⋅w→ = det r→v→w→ .
Quindi, il valore assoluto |(r→ ∧v→) ⋅w→|
è il volume del parallelepipedo identificato dai tre vettori (pensati applicati
nell’origine);
- In particolare,
det r→v→r→ ∧v→ = (r→∧v→)⋅(r→∧v→).
Questo numero è zero se i vettori r→
e v→
sono colineari. Altrimenti è positivo. Dunque, i tre vettori r→,
v→,
r→ ∧v→
(presi in quest’ordine e con r→
e v→
non colineari) subordinano in ℝ3
l’orientazione positiva.
Si noti che:
- Il prodotto vettoriale si definisce per vettori liberi; la definizione si estende
quindi al caso dei vettori applicati nel medesimo punto come si è detto
al paragrafo 3.1.2.
- Il prodotto vettoriale di due vettori è un vettore. Per contrasto, il
prodotto scalare di due vettori è un numero.
- Il prodotto vettoriale è nullo se e solo se i due vettori sono colineari.
Per contrasto, il prodotto scalare è nullo se e solo se i due vettori sono
ortogonali.
Infine, si noti che le regole per il calcolo del prodotto vettoriale sono definite in modo
da “mimare” quelle per il calcolo dei determinanti.
Osservazione 112 Il prodotto vettoriale può definirsi in particolare per
vettori complanari, per esempio per vettori del piano z = 0.
In tal caso il prodotto vettoriale è un vettore “verticale”, ossia parallelo
all’asse z. _
Osservazione sulla notazione La notazione col punto,
v→ ⋅w→,
per indicare il prodotto scalare è oggi universalmente
usata.
Invece, la notazione per il prodotto vettoriale non è cosìuniforme. La notazione
v→ ∧w→ si trova
principalmente in testi europei, mentre in testi americani (ed anche inglesi) il prodotto vettoriale
è indicato v→ ×w→.
3.6 Coordinate curvilinee nel piano e nello spazio
Il modo più comune per rappresentare i punti del piano, o dello spazio, usa
le coordinate cartesiane ortogonali. Però, punti del piano e dello spazio
possono rappresentarsi, oltre che in coordinate cartesiane ortogonali mediante
coordinate cartesiane oblique o anche con altri “sistemi di coordinate” che
generalmente costruiscono corrispondenze biunivoche tra i punti (del piano o dello
spazio) (o talvolta di opportuni loro s.insiemi) ed opportuni s.insiemi di
ℝ2 oppure
di ℝ3.
Per ragioni che vedremo, si parla in tal caso di coordinate curvilinee Noi
esamineremo prima le coordinate cartesiane oblique (nel piano. La semplice
estensione allo spazio è lasciata al lettore). Poi studieremo alcuni casi
particolari di coordinate curvilinee: vedremo l’uso delle coordinate polari e delle
coordinate ellittiche per rappresentare i punti del piano cartesiano e l’uso
delle coordinate cilindriche, sferiche ed ellittiche per rappresentare i punti
dello spazio, che supporremo dotato di un sistema di coordinate cartesiane
ortogonali.
Coordinate cartesiane oblique nel piano (e nello spazio). fissata l’origine
O,
tracciamo per essa due rette non coincidenti (tre rette non complanari
nello spazio). Queste rette si chiamano assi cartesiani obliqui. Si decida
quale è la prima retta, asse delle ascisse, la seconda, asse delle ordinate,
un verso positivo su di esse e un’unità di misura (che potrebbe anche
essere diversa. Noi assumeremo che sia la medesima). Da un punto
P
facciamo uscire due rette, parallele agli assi delle ordinate e delle ascisse. La retta
parallela all’asse delle ordinate interseca l’asse delle ascisse in un punto
P1 la cui distanza distanza
(con segno) da O si chiama
l’ascissa di P. In modo analogo
si definisce l’ordinata di P.
La coppia ordinata dell’ascissa e dell’ordinata rappresenta univocamente il punto
P. Si
veda la figura 3.6.
Un problema importante è di passare da un sistema di coordinate ad un altro.
Limitiamoci a studiare il caso di due sistemi di coordinate, uno un sistema di
coordinate cartesiane ortogonali del piano ed uno un sistema di coordinate
oblique. Provvisoriamente indichiamo con lettere greche le coordinate oblique:
ξ è l’asse delle ascisse
(oblique) ed η quello delle
ordinate. Indichiamo con i→
e j→ i
versori degli assi cartesiani ortogonali e siano
v→1 = i→ cos 𝜃 + j→ sin 𝜃,v→2 = i→ cos ϕ + j→ sin ϕ
i versori degli assi obliqui, si veda la figura 3.7.
Si conoscano le coordinate cartesiane ortogonali
(x,y) del punto
P. Le coordinate
oblique di P
sono le distanze dall’origine dei vettori dei punti
P1 e
P2, che
avranno forma
ξv→1,ηv→2
per certe scelte dei parametri ξ
e η. Poiché
v→1 e
v→2 sono versori, le
coordinate oblique di P
sono proprio i numeri ξ
e η, che
ora vogliamo calcolare. Ciò si fa notando che
xi→ + yj→ = ξv→1 + ηv→2 = ξ(i→ cos 𝜃 + j→ sin 𝜃) + η(i→ cos ϕ + j→ sin ϕ).
Uguagliando le componenti si ottiene immediatamente
ξ = y cos ϕ−x sin ϕ
sin(𝜃−ϕ) ,
η = x sin 𝜃−y cos 𝜃
sin(𝜃−ϕ) , x = ξ cos 𝜃 + η cos ϕ y = ξ sin 𝜃 + η sin ϕ.
Si noti che il denominatore è non nullo perchè gli assi obliqui
non coincidono. Si osservi un caso particolare: supponiamo che
ϕ − 𝜃 = π∕2. In questo
caso gli “assi obliqui” sono tra loro perpendicolari e si vuol rappresentare il medesimo
punto P
rispetto a due sistemi di assi cartesiani ortogonali ruotati l’uno rispetto all’altro.
Precisamente, il secondo sistema è ottenuto ruotando il primo dell’angolo
𝜃
(in senso positivo o negativo). Essendo in questo caso particolare
ϕ = 𝜃 + π∕2, le
coordinate (ξ,η)
sono date da
ξ = x cos 𝜃 + y sin 𝜃 η = −x sin 𝜃 + y cos 𝜃, x = ξ cos 𝜃 − η sin 𝜃 y = ξ sin 𝜃 + η cos 𝜃.
Coordinate polari nel piano. Sia
P il punto da rappresentare.
Si rappresenta P mediante
la sua distanza da O
e mediante l’angolo 𝜃
tra la retta r che
esce dall’origine O
e punta verso P
e il semiasse positivo delle ascisse. L’angolo si sceglie col segno in questo modo: si orienta
la retta r
da O verso
P; si riporta il semiasse
x > 0 sulla semiretta
r, ruotando dell’angolo
minore. L’angolo 𝜃
cosìottenuto si intende positivo se la rotazione è antioraria (si confronti con la
regola d’Ampère).
In questo modo si stabilisce una corrispondenza biunivoca tra i punti del piano
(x,y), escluso
O, e le coppie
di numeri (ρ,𝜃)
con ρ > 0 e
0 ≤ 𝜃 < 2π. Dunque, ogni
punto P del
piano (x,y), escluso
O, viene identificato dalla
coppia dei numeri ρ e
𝜃, che si chiamano le
coordinate polari di P. L’origine
invece è identificata da (0,𝜃)
per ogni 𝜃. Si veda la
figura 3.8. Il numero ρ si
chiama il definmodulo e 𝜃
si chiama l’ argomento}o anomalia}o anomalia di
P.
La relazione tra le coordinate cartesiane e le coordinate polari è data
da:
x = ρ cos 𝜃,y = ρ sin 𝜃.
nel contesto delle coordinate polari, il semiasse positivo delle ascisse si chiama
anche asse polare e il suo estremo, ossia l’origine, si chiama anche polo
Osservazione 113 Va notato che la corrispondenza (ρ,𝜃)↦(x,y)
è suriettiva ma non iniettiva; dunque non invertibile. Si trova una corrispondenza
biunivoca di ℝ2 ∖{0}
se (ρ,𝜃) ∈ (0, +∞) × [0, 2π).
Coordinate polari ellittiche piano. Siano assegnati due numeri positivi
a e
b. Le
coordinate polari ellittiche nel piano si ottengono rappresentando i punti
(x,y) mediante i
numeri (ρ,𝜃)
tali che
x = ρa cos 𝜃,y = ρb sin 𝜃.
Le curve coordinate delle coordinate polari od ellittiche. Torniamo alle
relazioni
x = ρa cos 𝜃,y = ρb sin 𝜃.
Queste relazioni identificano un punto
(x,y) del piano per
ogni scelta di (ρ,𝜃).
Si chiamano curve coordinate quelle ottenute da queste espressioni per
𝜃 fissato al variare
di r (rette per
l’origine) e per r
fissato al variare di 𝜃
(ellissi; nel caso particolare delle coordinate polari si hanno circonferenze).
Coordinate cilindriche nello spazio. Sia
P ≡ (x,y,z) un
punto dello spazio, riferito ad un sistema di coordinate cartesiane ortogonali. Il punto
Q ≡ (x,y, 0) si chiama la proiezione
ortogonale di P
sul piano z = 0.
Il punto Q
si può rappresentare mediante le sue coordinate polari
(ρ,𝜃) e quindi
P viene ad essere
rappresentato mediante (ρ,𝜃,z).
Quando si fa uso di questa rappresentazione si dice che si rappresenta lo spazio in
coordinate cilindriche, si veda la figura 3.9. Se invece delle coordinate polari, sul
piano si usano le coordinate ellittiche, le corrispondenti coordinate nello spazio si
chiamano cilindriche ellittiche
Le superfici coordinate delle coordinate cilindriche. Le curve coordinate
sono quelle curve che si ottengono tenendo fissi i valori di due parametri
e facendo variare il terzo. Sono quindi rette per l’origine, circonferenze
(o ellissi) e rette verticali. Però nello spazio si possono anche definire le
superfici coordinate, ottenute tenendo fisso un parametro e facendo
variare gli altri due. Quindi, nel caso delle coordinate cilindriche ellittiche,
le superfici coordinate sono cilindri ellittici di asse parallelo all’asse
z (ottenuti tenendo fisso il
valore di ρ); piani per l’asse
z (ottenuti tenendo fisso il
valore di 𝜃); piani perpendicolari
all’asse z (ottenuti tenendo
fisso il valore di z).
Coordinate sferiche ed ellittiche nello spazio. Le coordinate sferiche nello
spazio sono l’analogo delle coordinate polari nel piano. Per rappresentare un punto
P(x,y,z), si costruisce la
retta congiungente O
con P. Si
rappresenta P
mediante (r,𝜃,ϕ)
dove r è la
distanza di P da
O e ancora si chiama
l’argomento di P;
𝜃 è l’argomento
della proiezione Q
di P sul
piano z = 0,
ϕ è l’angolo tra
il versore ν→ che
sulla retta da O
a P punta
verso P ed il
versore k→.
L’ampiezza di quest’angolo si intende compresa tra
0 e
π.
Dunque, si veda la figura 3.10, P
si rappresenta anche con la terna (r,𝜃,ϕ)
con
r ≥ 0,0 ≤ 𝜃 < 2π,0 ≤ ϕ ≤ π.
Questi numeri si chiamano le coordinate sferiche di
P. La
relazione tra le coordinate cartesiane e le coordinate sferiche è la seguente:
x = r cos 𝜃 sin ϕ,y = r sin 𝜃 sin ϕ,z = r cos ϕ.
Il numero r si chiama ancora
modulo, il numero 𝜃 si chiama
longitudine mentre il numero ϕ
si chiama colatitudine. Siano dati ora tre numeri positivi
a,
b e
c.
Le coordinate ellittiche di un punto nello spazio sono le coordinate
(ρ,𝜃,ϕ) che si
ottengono imponendo
x = ra cos 𝜃 sin ϕ,y = rb sin 𝜃 sin ϕ,z = rc cos ϕ.
Le superfici coordinate delle coordinate sferiche ed
ellittiche. Nel caso delle coordinate sferiche, le superfici coordinate
sono sfere di centro l’origine (ottenute tenendo fisso il valore di
r); piani per l’asse
z (ottenuti fissando il valore
di 𝜃; (semi)coni circolari di
asse sull’asse z (ottenuti
tenendo fisso il valore di ϕ).
Per esercizio, se ne identifichino le curve coordinate e si identifichino anche le curve
e le superfici coordinate delle coordinate ellittiche.
3.7 Funzioni da ℝ
in ℝn
Studiamo ora le proprietà di limite e continuità delle funzioni definite su sottoinsiemi di
ℝ ed a valori
in ℝn. Sia
x→ ∈ ℝn un vettore
e siano xi
le sue componenti. E’ utile tener presente le disuguaglianze seguenti (si vedano
le (3.3)):
- Per ogni i
vale |xi|≤|x→|;
- Esiste un numero M = Mn,p
tale che |x→|p ≤ M∑
i=1n|x
i|.
Le funzioni da ℝ
in ℝ sono
state studiate nel corso di Analisi Matematica 1. E’ facile adattare gli argomenti
visti nel corso di Analisi Matematica 1 al caso di funzioni a valori vettoriali. Per
l’uso che a noi servirà, consideriamo funzioni definite su un intervallo
I, aperto o meno, limitato
o meno, a valori in ℝn.
Dunque, si specifica la funzione assegnando ad ogni valore
t ∈ I un vettore
x→(t) ∈ ℝn, ossia assegnando
le sue n
componenti. Si costruisce cosìuna funzione
t →x→(t) = x1(t)
x2(t) ⋮
xn(t) = x1(t)e→1+x2(t)e→2+⋯+xn(t)e→n.
Nel caso di ℝ2
o di ℝ3
scriveremo anche
x→(t) = x(t)i→ + y(t)j→ + z(t)k→.
Notiamo che le componenti di x→(t)
sono funzioni da ℝ
in ℝ e
quindi le nozioni apprese nel corso di Analisi 1 possono essere applicate a ciascuna
componente. Ora definiamo:
Si fissi un punto t0. Il
punto t0 può essere
un punto di I o
anche un estremo di I
che non gli appartiene.
Si dice che
lim t→t0x→(t) = l→
quando assegnata una
qualsiasi palla
B(l→,𝜖)
centrata in
l→
esiste un intorno
I𝜖(t0)
tale che se
t ∈ I𝜖 ∩ I,
t≠t0,
allora
x→(t) ∈ B(l→,𝜖).
In simboli,
∀𝜖∃δ|t ∈ Ie0 < |t − t0| < δ ⇒|x→(t) −l→| < 𝜖.
Se
t ∈ I
e inoltre
lim t→t0x→(t) = x→(t0)
si dice che la funzione è continua in
t0.
Si lascia per esercizio di definire i limiti per
t → +∞ e per
t →−∞,
sulla falsariga della definizione del limite di successioni, vista al
paragrafo 3.3. Si noti però che non è possibile definire limiti uguali a
±∞. Se
x→(t)
non rimane limitata allora possiamo definire solamente
lim |x→(t)| = +∞ e si
ricade in un caso già trattato nel corso di Analisi Matematica 1 perch’e la funzione
t →|x→(t)| è una
funzione da ℝ in
s’e. Siano xi(t) le
componenti di x→(t)
ed li quelle
di l→. Il
teorema seguente è analogo al Teorema è.
Teorema 114 Vale lim x→(t) = l→
se e solo se per ogni i
vale lim xi(t) = li.
Una funzione t →x→(t)
da ℝ
in ℝn
è continua se e solo se ciascuna sua componente è una funzione continua da
ℝ
in ℝ.
Noto ciò, è immediato dedurre il risultato seguente:
Teorema 115 Siano
t →x→(t)
e
t →y→(t)
due funzioni da
ℝ
in
ℝn
definite sul medesimo intervallo
I
ed ambedue continue e sia
t → k(t)
una funzione da
ℝ
in
ℝ
definita su
I
e continua. Le funzioni
t → k(t)x→(t),t →x→(t) + y→(t),t →x→(t) ⋅y→(t)
(il punto indica il prodotto scalare calcolato per ogni valore di t)
sono continue. Se n = 3,
anche la funzione t →x→(t) ∧y→(t)
è continua.
Si lascia per esercizio di enunciare i teoremi corrispondenti per i limiti.
- i simboli di Landau Si dice che x→(t)
è un infinitesimo per t → t0
quando
lim t→t0x→(t) = 0.
Siano x→(t) e
y→(t)
due funzioni definite sul medesimo intervallo
I e se ne vogliano
studiare le relazioni per t → t0.
Diciamo che:
-
- i) x→ = O→(y→)
quando esistono un numero M
ed un intorno J
di t0
tali che:
t ∈ I ∩ J ⇒|x→(t)|≤ M|y→(t)|.
-
- ii) x→ = o→(y→)
quando |y(t)|≠0
per t≠t0
in un intorno di t0
e inoltre
lim t→t0|x→(t)|
|y→(t)| = 0.
In queste definizioni le due funzioni x→(t)
e y→(t)
potrebbero avere valori in spazi di dimensione diversa. In particolare,
y→(t)
potrebbe essere una funzione a valori in ℝ.
Se y(t)
prende valori in ℝ
ed è costantemente uguale ad 1,
la condizione x→ = o→(1)
vul dire che x→(t)
è un infinitesimo (sottinteso, per t → t0).
Sia t0 punto interno
di I. Si dice che
un vettore l→ è
la derivata di x→(t)
quando
l→ = lim t→t0x→(t) −x→(t0)
t − t0 .
La derivata si indica con uno dei soliti simboli,
dx→(t0)
dt ,x→′(t
0),x→̇(t0),Dx→(t0),Dt0x→ecc.
Se t indica il tempo e se
x→(t) indica la posizione di
un punto all’istante t,
allora il quoziente
x→(t) −x→(t0)
t − t0
indica la velocità media del punto, nell’intervallo di tempo
(t0,t);
e quindi la derivata si interpreta come velocità del punto all’istante
t.
Usando le disuguaglianzein (3.3), si vede che
Teorema 116 La funzione
x→(t)
è derivabile in
t0
se e solo se ciascuna sua componente è derivabile in
t→0
e inoltre
x→′(t
0) = x1′(t
0)
x2′(t
0) ⋮
xn′(t
0) .
Dunque, una funzione derivabile in un punto
t0
è ivi continua.
In modo del tutto analogo si definiscono le derivate direzionali. Le usuali regole di
calcolo delle derivate si possono applicare alle singole componenti del vettore
x→(t) e
quindi, per esempio, vale ancora la proprietà di linearità della derivata:
Dt0{x→(t) + y→(t)} = x→′(t
0) + y→′(t
0).
Teorema 117 Siano x→(t)
ed y→(t) derivabili in
t0. I prodotti scalare
e vettoriale sono
derivabili in t0
e valgono le uguaglianze
|
d
dt x→(t) ⋅y→(t) = x→′(t) ⋅y→(t) + x→(t) ⋅y→′(t),
d
dt x→(t) ∧y→(t) = x→′(t) ∧y→(t) + x→(t) ∧y→′(t).
|
Dim. Proviamo l’asserto per il prodotto vettoriale. Bisogna calcolare
lim h→0x→(t + h) ∧y→(t + h) −x→(t) ∧y→(t)
h .
Aggiungendo e sottraendo al numeratore
x→(t) ∧y→(t + h) si
vede che la derivata è uguale a
lim h→0x→(t + h) −x→(t)
h ∧y→(t+h)+lim h→0x→(t)∧y→(t + h) −y→(t)
h = x→′(t)∧y→(t)+x→(t)∧y→′(t)
perchè
lim h→0y(t + h) = y(t)
perché la funzione y→(t),
essendo derivabile, è anche continua La dimostrazione per il prodotto scalare è
simile. _
Osservazione 118 Nella regola per la derivata del prodotto vettoriale i fattori
non possono scambiarsi; invece la derivata del prodotto scalare non dipende
dall’ordine dei fattori. _
In particolare:
Teorema 119 Sia x→(t)
una funzione derivabile a valori in ℝn
e tale che |x→(t)|≡ 1.
Allora, x→′(t) ⊥x→(t) .
Dim. Infatti, derivando i due membri dell’uguaglianza
1 = |x→(t)|2 = x→(t) ⋅x→(t)
si trova
2x→′(t) ⋅x→(t) ≡ 0
ossia
x→′(t) ⊥x→(t).
Ovviamente, se x→(t)
è derivabile in t0,
vale la prima formula degli incrementi finiti
x→(t) = x→(t0) + x→′(t
0)(t − t0) + o→(t − t0).
Osservazione 120 Va esplicitamente notato che la seconda formula degli incrementi
finiti, ossia il Teorema di Lagrange, NON vale. Per rendersi conto di ciò, consideriamo
la funzione x→(t) = x(t)i→ + y(t)j→.
Il Teorema di Lagrange può applicarsi alle due componenti separatamente,
ottenendo
x(t′) − x(t″) = x′(c
1)(t′− t″),y(t′) − y(t″) = y′(c
2)(t′− t″)
e generalmente c1≠c2. _
Se le singole componenti di x→(t)
sono ciascuna derivabile 2
volte, potremo introdurre le derivate seconde e, in generale, le derivate
k-me in
t0. Se ciascuna
componente ammette k
derivate in t0
si può anche scrivere la formula di Taylor con resto in forma di Peano,
x→(t) = x→(t0) + ∑
j=1kx→(j)(t
0)
j! (t − t0)j + o→(t − t
0)k.
Se t →x→(t) è definita
su [a,b]
e ciascuna sua componente è integrabile, si definisce
∫
abx→(t)dt
come quel vettore che ha per componenti i numeri
∫
abx
i(t)dt.
Capitolo 4
Funzioni da ℝn
in ℝm
Studiamo ora le funzioni di più di una variabile; ossia funzioni
F→(x→)
a valori in ℝm,
della variabile x→ ∈ ℝn,
in generale con n≠m.
Ovviamente, le prime proprietà da studiare saranno le proprietà
relative ai limiti ed alla continuità. Come vedremo, non si incontrano
situazioni sostanzialmente diverse da quelle delle funzioni da
ℝ in
ℝ
(però le proprietà relative agli estremi saranno tipiche delle funzioni a
valori reali). Differenze profonde si troveranno invece nello studio della
differenziabilità.
4.1 Limiti e continuità
Ricordiamo che col simbolo |r→|
intendiamo la norma di r→,
senza esplicitamente indicare la dimensione del vettore. Per esempio,
|
se r→ = x ∈ ℝ allora |r→| = x2 = |x|;
se r→ = (x,y) allora |r→| = x2 + y2;
se r→ = (x,y,z) allora |r→| = x2 + y2 + z2.
|
Se vorremo specificare che la norma è quella di
ℝn allora
scriveremo
|r→|ℝn.
Sia F→(r→) una funzione
definita su un insieme Ω
di ℝn, a valori
in ℝm e sia
r→0 un punto di
accumulazione di Ω.
Diremo che
lim r→→r→0F→(r→) = L→
Se per
ogni 𝜖 > 0
esiste un intorno
I𝜖(r→0)
del punto
r→0
tale che
per
ogni r→ ∈ Ω ∩ I𝜖(r→0),
r→≠r→0
si ha
|F→(r→) −L→|ℝm < 𝜖.
In simboli:
∀𝜖 > 0∃I𝜖(r→0)|∀r→ ∈ Ω ∩I𝜖(r→0) −{r→0}⇒|F→(r→) −L→|ℝm < 𝜖.
Se L→ = 0 allora si dice
che la funzione F→(r→) è
infinitesima per r→ →r→0.
Se accade che F→(r→)
è definita in r→0 e
se inoltre lim r→→r→0F→(r→) = F→(r→0), allora
si dice che F→(r→) è
continua in r→0.
Si noti che la definizione di limite e quella di continuità sono formalmente analoghe a quelle
note per funzioni di una variabile. la differenza importante da tener presente è che ora il simbolo
I𝜖(r→0) indica una palla
aperta di centro r→0.
E’ un po’ diversa la definizione dei limiti infiniti o per
r→
tendente ad infinito, perché non si definisce il limite “direzionale”. Piuttosto, si
definisce
Sia
Ω
un insieme illimitato. Si dice che
lim |r→|ℝn→+∞F→(r→) = L→
se per
ogni
𝜖 > 0
esiste
δ
tale che se
|r→|ℝn > δ
e
r→ ∈ Ω
si ha
|F→(r→) − L|ℝm < 𝜖.
Sia
r→0
punto di accumulazione di
Ω.
Si dice che
lim r→→r→0|F→(r→)|ℝm = +∞
se per
ogni
𝜖 > 0
esiste
δ > 0
tale che se
r→ ∈ Ω,
r→≠r→0
e
|r→ −r→0|ℝn < δ
si ha
|F→(r→)|ℝm > 𝜖.
In queste definizioni, per completezza, abbiamo usato gli indici
ℝn e
ℝm per
indicare esplicitamente gli spazi nei quali le norme vanno lette; da ora in poi però
ometteremo tali indici.
Osservazione 121 Una funzione F→(r→)
da ℝn
in ℝm
è infinitesima (per r→ →r→0 →
oppure per |r→|→ +∞)
se e solo se |F→(r→)|
è infinitesima come funzione da ℝn
in ℝ. _
Si rileggano i teoremi sui limiti delle funzioni di una variabile, identificando quelle
dimostrazioni che, grazie alle proprietà della norma, si ripetono senza alcuna
modifica nel caso delle funzioni di più variabili. Naturalmente non rientrano tra
queste quelle dimostrazioni che dipendono dall’ordine tra i numeri reali, come il
teorema delle funzioni monotone e le sue conseguenze. Sottolineiamo che in
particolare valgono:
- Il teorema di unicità del limite;
- il teorema di limitatezza locale;
- i teoremi che correlano i limiti e la continuità con le operazioni. Naturalmente,
tra funzioni a valori vettoriali non si fanno divisioni; e il teorema del
prodotto va applicato al prodotto scalare o anche, quando m = 3,
al prodotto vettoriale: i prodotti scalari e vettoriali di funzioni continue sono
funzioni continue;
- i teoremi relativi ai limiti di funzioni composte;
- per funzioni a valori in ℝ,
il teorema di confronto per i limiti e il teorema di permanenza del segno;
- il teorema di confronto per gli infiniti e gli infinitesimi.
In particolare, vale
Lemma 122 Sia
lim r→→r→0 F→(r→)
|r→ −r→0| = 0.
Sia
lim t→t0r→(t) = r→0
ed esista un intorno di t0
su cui la funzione r→(t)
non prende valore r→0.
In tal caso vale
lim t→t0 F→(r→(t))
|r→(t) −r→0| = 0.
Notiamo un caso particolare del teorema sulla continuità delle funzioni composte, già
usato nel corso di Analisi Matematica 1, trattando le equazioni differenziali:
Teorema 123 Sia f(x→)
un funzione da ℝn
in ℝm,
continua su un insieme Ω.
Sia x→(t)
una funzione continua della variabile reale t ∈ [a,b],
a valori in Ω.
La funzione composta f(x→(t))
è continua su [a,b].
Come si è detto, una funzione che ha limite zero (per
r→ →r→0) si chiama ancora un
infinitesimo (per r→ →r→0);
e si può istituire un confronto tra gli infinitesimi, esattamente come nel caso di
funzioni di una variabile. Per esempio, il simbolo
F→ = o(|r→ −r→0|)
significa
lim r→→r→0 |F→(r→)|
|r→ −r→0| = 0.
Usando il linguaggio degli infinitesimi, possiamo enunciare:
Teorema 124 Si ha
lim r→→r→0F→(r→) = L→
se e solo se la funzione F→(r→) −L→
è infinitesima per r→ →r→0.
Infine, notiamo che le disuguaglianze (3.3) permettono di provare:
Teorema 125 Siano Fi(r→)
le componenti della funzione F→(r→)
da ℝn
in ℝm.
Si ha lim r→→r→0F→(r→) = L→
se e solo se per ogni indice i
vale lim r→→r→0Fi(r→) = Li,
ove Li
sono le componenti del vettore L→.
Si enunci il risulato analogo per i limiti per
|r→|→ +∞.
Nonostante che abbiamo insistito sulla completa corrispondenza che intercorre
tra definizioni e teoremi in una e più variabili, bisogna sottolineare una
importante dissimmetria, che illustriamo con riferimento a funzioni da
ℝ2 in
ℝ2. Sia
quindi
F→(x,y) = f(x,y)i→ + g(x,y)j→.
Da
|
|f(x,y)|≤|F→(x,y)|≤|f(x,y)| + |g(x,y)|
|g(x,y)|≤|F→(x,y)|≤|f(x,y)| + |g(x,y)|
|
si vede che F→(x,y)
è infinitesima se e solo se ambedue le sue componenti lo sono; è continua
se e solo se ambedue le sue componenti lo sono; ossia, come asserito dal
Teorema 125, limiti e continuità possono studiarsi esaminando separatamente le
due componenti dei valori assunti dalla funzione, ossia le due componenti
f(x) ed
g(x) di
F→(x).
Ciò non accade nello spazio di partenza; ossia le due componenti
x ed
y non possono
trattarsi separatamente. Per vedere questo, basta considerare una sola delle componenti di
F→(x,y), per esempio la
funzione a valori reali f(x,y).
La funzione
|
ϕ(x) = lim y→y0f(x,y)
| (4.1) |
può essere definita per ogni x,
e può esistere lim x→x0ϕ(x); però tale
limite è in generale diverso da lim (x,y)→(x0,y0)f(x,y),
come mostra l’esempio seguente:
Esempio 126 Sia
f(x,y) = 1se|x| < |y| 0 se |x| ≥ |y|.
La funzione
f(x,y)
è priva di limite per
(x,y)
tendente a zero, mentre
lim x→0 lim y→0f(x,y) = 0, lim y→0 lim x→0f(x,y) = 1.
Si veda la figura 4.1.
Può anche accadere che esista
lim (x,y)→(x0,y0)f(x,y)
ma che non esista il limite che definisce
ϕ(x)
in (4.1), come mostra l’esempio seguente:
Esempio 127 Sia
f(x,y) = x sgn(y) .
Essendo |f(x,y)|≤|x|,
il teorema di confronto dei limiti mostra che
lim (x,y)→(0,0)f(x,y) = 0;
ma,
lim y→0f(x,y)
esiste soltanto se x = 0. _
Infine, ricordiamo che successione è il termine che si usa per designare
una funzione definita sui numeri naturali. Una successione a valori in
ℝm si indicherà col simbolo
(r→n) o, più frequentemente
{r→n}.
Come nel caso particolare delle successioni a valori reali, le definizioni e i
teoremi sui limiti delle successioni sono casi particolari di quelli relativi alle
funzioni.
4.1.1 Funzioni continue su insiemi
E’ possibile provare l’analogo del Teorema di Bolzano-Weierstrass: ogni successione limitata
a valori in ℝn
ammette sottosuccessioni convergenti. Un insieme
Ω si dice compatto, quando
ogni successione in Ω
ammette sottosuccessioni convergenti a punti di
Ω. Si
può ancora provare:
Teorema 128 Un insieme
Ω
è compatto se e solo se è limitato e chiuso.
Grazie a ciò, si prova l’analogo del Teorema di Weierstrass con la medesima
dimostrazione vista per funzioni di una variabile. Diremo che:
- un punto r→0
è punto di minimo, o di massimo, per una funzione f(r→)
a valori reali, se vale, rispettivamente,
f(r→) ≥ f(r→0)oppuref(r→) ≤ f(r→0)
per ogni r ∈ Ω;
- diremo che la funzione F→(r→),
da ℝn
in ℝm
è uniformemente continua se per ogni 𝜖 > 0
esiste δ > 0
tale che
r→ ∈ Ω,r→0 ∈ Ω,|r→ −r→0| < δimplica|F→(r→) −F→(r→0)| < 𝜖.
Vale:
Teorema 129 Sia f(r→)
una funzione a valori reali definita e continua su un compatto K ⊆ ℝn.
La funzione f(r→)
ammette in K
sia punti di minimo che punti di massimo.
Il teorema di esistenza degli zeri, equivalentemente quello dei valori intermedi, richiede,
per funzioni di una variabile, di lavorare su intervalli. Gli insiemi aperti e connessi
sono gli analoghi degli intervalli aperti, nel senso che per essi vale il teorema
seguente:
Teorema 130 Sia Ω
un insieme aperto e connesso e sia f(r→)
una funzione a valori reali e continua su Ω.
Se r→0
e r→1
sono due punti di Ω,
la funzione assume ogni valore c
compreso tra f(r→0)
e f(r→1).
Dim. Sia
f(r→0) = a,f(r→1) = b.
Se è possibile congiungere r→0
e r→1 con un segmento
contenuto in Ω,
si considera la restrizione della funzione a tale segmento. Si trova una funzione di
una sola variabile, continua e definita su un intervallo, che assume i valori
a e
b. Dunque assume anche
il valore intermedio c.
Nel caso che i due punti si congiungano con una poligonale, ossia, con un numero
finito di segmenti, si procede in modo analogo sui singoli segmenti. _ Esistono
versioni del teorema precedente anche per funzioni a valori vettoriali. Si veda per
esempio il paragrafo 7.5.2.
4.2 Le proprietà di differenziabilità
Per lo studio di queste proprietà, conviene separare lo studio delle funzioni a valori in
ℝ da quello delle
funzioni a valori in ℝm
con m > 1.
4.2.1 Il differenziale delle funzioni a valori reali
Quando la funzione f(x,y)
dipende da due variabili, la derivata parziale rispetto ad
x è la funzione
sia di x
che di y
definita da
lim h→0f(x + h,y) − f(x,y)
h .
Per indicare questa funzione si usa uno dei simboli
∂
∂xf(x,y),fx(x,y).
In modo analogo si definisce la derivata parziale rispetto ad
y e
quella rispetto alle ulteriori variabili nel caso che la funzione dipenda da più di due
variabili. Si noti esplicitamente che trattando delle equazioni differenziali si è
dovuto richiedere però non la sola esistenza delle derivate parziali, ma la loro
continuità. In effetti, la sola esistenza delle derivate parziali è un concetto molto
debole. Infatti:
Esempio 131 L’esistenza delle derivate parziali in un punto (x0,y0),
non implica la continuità della funzione in tale punto, come mostra l’esempio
seguente:
f(x,y) = 0sex ⋅ y = 0 1 altrimenti, (x0,y0) = (0, 0).
Per contrasto, si ricordi che l’esistenza della derivata prima in un punto di una funzione di
una sola variabile, implica la continuità in tale punto. Ricordiamo che la
dimostrazione di ciò segue dalla prima formula degli incrementi finiti e che
praticamente tutte le proprietà delle funzioni derivabili di una variabile seguono
dalla prima oppure dalla seconda formula degli incrementi finiti. Dunque, se si vuol
sperare di ripetere, per le funzioni di più variabili, una teoria simile a quella delle
funzioni di una variabile, dovremo dare condizioni per l’esistenza di una formula
analoga alla prima formula degli incrementi finiti: ossia, nel caso di funzioni
di due variabili, vorremo condizioni perchè valga la formula seguente
|
f(x,y) − f(x0,y0) = a(x − x0) + b(y − y0) + o(|(x − x0,y − y0)|).
| (4.2) |
Il risultato che vogliamo provare è:
Teorema 132 Sia f(x,y)
una funzione di due variabili. Supponiamo che essa ammetta ambedue le derivate
parziali in ogni punto (x,y)
di un intorno di (x0,y0)
e che queste siano continue in tale intorno. Esistono numeri a,
b
per i quali vale la formula (4.2), ed è:
a = fx(x0,y0),b = fy(x0,y0).
La dimostrazione è in appendice. Passando al limite per
dist((x,y), (x0,y0)) tendente a zero
in (4.2) si vede che lim f(x,y) = f(x0,y0).
Si ha quindi in particolare:
Corollario 133 Se una funzione ha derivate parziali continue un intorno di
(x0,y0),
essa è continua in (x0,y0).
Argomenti del tutto analoghi valgono per funzioni di tre o più variabili:
Teorema 134 Una funzione di n
variabili le cui n
derivate prime esistono e sono continue su un aperto
Ω è continua
su Ω e
per essa vale
|
f(ξ1,ξ2,…,ξn) = f(x1,x2,…,xn) + ∑
i=1n(ξi − xi)f
xi(x1,x2,…,xn)
+ o(|h→|),h→ = (ξ1 − x1), (ξ2 − x2),…, (ξn − xn) .
|
Si chiama differenziale della funzione f
in r→ = x1x2…xn ′ la trasformazione
che al vettore (y1,…,yn)
associa il numero
∑
i=1ny
ifxi(x1,x2,…,xn).
Una funzione dotata di differenziale si chiama differenziabile. Il vettore
fx1(r→)
fx2(r→) ⋮
fxn(r→) r→ = x1
x2
⋮ xn
si chiama il gradiente della funzione f(r→)
e si indica col simbolo ∇f(r→).
Il simbolo ∇
si legge “grad”, oppure “del” od anche “nabla”. Usando questo simbolo, la (4.3) si
scrive
f(r→) − f(r→0 →) = ∇f(r→0 →) ⋅ (r→ −r→0 →) + o(|r→ −r→0 →|).
Si chiama piano tangente al grafico di
f(r→) nel
punto r→0 = (x01,…,x
0n)
il grafico della funzione
r→ →r→0 + ∇f(r→0) ⋅ (r→ −r→0).
Dunque, l’equazione del piano tangente è
y→ = r→0 + ∇f(r→0) ⋅ (r→ −r→0).
Il vettore ∇f(r→0)
è ortogonale al piano tangente. Per definizione,
si chiama il vettore normale al grafico di
f(r→)
nel punto r→0,f(r→0).
Si veda la figura 4.2.
Una funzione dotata di derivate parziali prime continue su un aperto
Ω si chiama una
funzione di classe C1(Ω)
e si scrive f ∈ C1(Ω). Si noti
che, per noi, il gradiente è un vettore colonna. D’altra parte, il differenziale, come trasformazione da
ℝn, dotato della base
canonica, ad ℝ, si rappresenta
mediante una matrice 1 × n,
ossia mediante un vettore riga. Il vettore riga che rappresenta il differenziale è il
trasposto del gradiente. Diciamo infine che si chiamano punti stazionari di
f(r→) i punti nei quali si
annulla il gradiente ∇f(r→).
Tali punti si chiamano anche punti estremali o punti critici
4.2.2 Regole di derivazione
Dato che la derivata parziale rispetto ad
x di una funzione
f(x,y) si calcolano fissando prima
il valore di y, e lavorando
con la funzione della sola x,
si hanno immediatamente le regole seguente:
|
∂
∂xaf(x,y) = a ∂
∂xf(x,y)∀a ∈ ℝ;
∂
∂x f(x,y) + g(x,y) = ∂
∂xf(x,y) + ∂
∂xg(x,y);
∂
∂x f(x,y)g(x,y) = ∂
∂xf(x,y) g(x,y) + f(x,y) ∂
∂xg(x,y) ;
∂
∂tf(x(t),y) = ∂
∂xf(x(t),y) x′(t).
|
Però nello studio della funzione composta si incontrano casi più complessi: può
essere che sia x
che y
vengano a dipendere dalla medesima variabile, ossia che si voglia calcolare
d
dtf(x(t),y(t)).
In questo caso si ha:
Teorema 135 Sia f(x,y)
differenziabile in ogni punto di una regione
Ω ⊆ ℝ2 e sia
(x(t),y(t)) una funzione
derivabile di t ∈ (a,b)
a valori in Ω.
Allora per ogni t
si ha:
|
d
dtf(x(t),y(t)) = fx(x(t),y(t))ẋ(t) + fy(x(t),y(t))ẏ(t).
| (4.3) |
Dim. Si fissi un punto t0
in cui si vuol calcolare la derivata, e si ponga
a = fx(x(t0),y(t0)),
b = fy(x(t0),y(t0)). Si
ha:
|
f(x(t),y(t)) − f(x(t0),y(t0)) = a[x(t) − x(t0)] + b[y(t) − y(t0)]
+ o(|(x(t) − x(t0),y(t) − y(t0))|)
= [aẋ(t0) + bẏ(t0)](t − t0) + o(t − t0) + o(|(x(t) − x(t0),y(t) − y(t0))|).
|
Notando che
o(|(x(t) − x(t0),y(t) − y(t0))|)
|(x(t) − x(t0),y(t) − y(t0))| ⋅|(x(t) − x(t0),y(t) − y(t0))|
t − t0
si vede che
o(|(x(t) − x(t0),y(t) − y(t0))|) = o(t − t0).
Infatti
o(|(x(t) − x(t0),y(t) − y(t0))|)
|(x(t) − x(t0),y(t) − y(t0))|
tende a zero per il Lemma 122 mentre
|(x(t) − x(t0),y(t) − y(t0))|
t − t0
rimane limitata, come si vede dalla seconda formula degli incrementi finiti applicata
sia ad x(t)
che ad y(t):
|
|(x(t) − x(t0),y(t) − y(t0))|
t − t0 = (ẋ (c))2 + (ẏ (d))2.
|
Sia ora
g(t) = f(x(t),y(t)).
L’uguaglianza
|
g(t) − g(t0) = [aẋ(t0) + bẏ(t0)](t − t0) + o(t − t0)
+ o(|(x(t) − x(t0),y(t) − y(t0))|)
= [aẋ(t0) + bẏ(t0)](t − t0) + o(t − t0)
|
mostra che g(t) è
derivabile per t = t0,
con
ġ(t) = d
dtf(x(t),y(t)) = aẋ(t0) + bẏ(t0).
Osservazione 136 Si noti che usando il Lemma 122, si è implicitamente
assunto che in un opportuno intorno di t0
la funzione (x(t),y(t))
non prenda valore (x(t0),y(t0)).
Si provi per esercizio che questa condizione può rimuoversi. _
Naturalmente, il Teorema 135 si estende al caso di funzioni di
n
variabili e, ricordando il Teorema 134, possiamo enunciare:
Corollario 137 Sia f(r→) ∈ C1(Ω)
e sia r→(t)
una funzione di t ∈ (a,b)
a valori in Ω,
derivabile. Allora, la funzione composta f(r→(t))
è derivabile su (a,b)
ed inoltre:
d
dtf(r→(t)) = ∇f(r→(t)) ⋅r→̇(t)
(il simbolo
⋅
indica il prodotto scalare).
Sia ora x = x(u,v),
y = y(u,v). Applicando il teorema
precedente alla variabile u,
con v fissato, e quindi
alla variabile v,
con u
fissato si trova:
Teorema 138 Sia f(x,y) ∈ C1(Ω).
Siano x = x(u,v),
y = y(u,v) due funzioni
definite su Ω ̃ e
di classe C1(Ω ̃), a
valori in Ω.
Valgono le uguaglianze
|
∂
∂uf(x(u,v),y(u,v)) = fx(x(u,v),y(u,v))xu(u,v) + fy(x(u,v),y(u,v))yu(u,v)
= ∇f(x(u,v),y(u,v)) ⋅xu(u,v)
yu(u,v) ,
∂
∂vf(x(u,v),y(u,v)) = fx(x(u,v),y(u,v))xv(u,v) + fy(x(u,v),y(u,v))yv(u,v)
= ∇f(x(u,v),y(u,v)) ⋅xv(u,v)
yv(u,v)
|
(il punto indica il prodotto scalare di vettori colonna). Questa formula si chiama anche
formula della derivazione a catena. Consideriamo ora un caso particolare: sia
x = tv1,
y = tv2. In questo
caso, i punti (x0 + tv1,y
0 + tv2)
sono punti di una retta nella direzione del vettore
v→ = (v1,v2), uscente
da (x0,y0).
La derivata
d
dtf(x0 + tv1,y
0 + tv2)
calcolata per t = 0 si chiama la
derivata secondo il vettore v→
della funzione e si indica col simbolo
∂f
∂v→(x,y).
Dal Teorema 135 segue che, se f(x,y)
è di classe C1,
∂f
∂v→(x,y) = fx(x,y)v1 + f
y(x,y)v2 = ∇f(x,y) ⋅v→.
Se v→
è un versore, allora si parla di derivata direzionale nella direzione
v→. E’
facile estendere gli argomenti precedenti a funzioni di tre o più variabili.
4.2.3 La direzione del gradiente e la direzione di massima velocità
crescita
Sia f(r→)
una funzione differenziabile a valori reali e sia
r→0 un
punto del suo dominio, che supponiamo aperto. fissiamo un segmento uscente da
r→0, dato
da
|
r→ = r→0 + tv→,t ∈ (−𝜖,𝜖).
| (4.4) |
Il numero 𝜖
si sceglie piccolo, in modo che il segmento sia contenuto nel dominio della funzione, e
v→ è un versore.
La derivata in t = 0
della funzione f(r→0 + tv→)
rappresenta la velocità di variazione dei valori della restrizione di
f(r→) al
segmento (4.4). E’
d
dtf(r→0 + tv→)|t=0 = ∇f(r→0) ⋅v→.
Questo numero rappresenta la componente di
∇f(r→0) lungo
v→
e quindi il suo valore assoluto è sempre minore di
|∇f(r→0)|; è uguale quando
accade che v→
è il versore
v→ = ∇f(r→0)
|∇f(r→0)|.
In questo caso si ha anche
∇f(r→0) ⋅v→ = |∇f(r→0)|;
ossia, la funzione f(r→)
ha massima velocità di crescita nella direzione e verso di
∇f(r→0); nel
verso opposto essa ha massima velocità di decrescita.
4.2.4 Le funzioni definite tramite integrali
Sia f(x,y)
una funzione continua su un rettangolo chiuso
[a,b] × [c,d]. Per ogni fissata
coppia di numeri x ∈ [a,b]
e y ∈ [c,d] si
può definire il numero
ϕ(x,y) = ∫
cyf(x,s)ds.
Si trova così una seconda funzione definita su
[a,b] × [c,d]. Vale:
Teorema 139 La funzione f(x,y)
sia continua sul rettangolo chiuso R.
Allora, la funzione ϕ(x,y)
è continua in R.
Dim. Si scriva
|ϕ(x,y) − ϕ(x′,y′)|≤|ϕ(x,y) − ϕ(x′,y)| + |ϕ(x′,y) − ϕ(x′,y′)|.
Vogliamo provare che per ogni η > 0
esiste σ > 0
tale che se
d((x,y), (x′,y′)) < σ
allora vale
|
|ϕ(x,y) − ϕ(x′,y)| < η∕2,
| (4.5) |
|
|ϕ(x′,y) − ϕ(x′,y′)| < η∕2.
| (4.6) |
Studiamo (4.5):
|
|ϕ(x,y) − ϕ(x′,y)| = ∫
cyf(x,s)ds −∫
cyf(x′.s)ds
= ∫
cy f(x,s) − f(x′,s) ds ≤∫
cy f(x,s) − f(x′,s) ds
≤∫
cd f(x,s) − f(x′,s) ds.
|
La funzione f(x,y)
è continua sul rettangolo limitato e chiuso
R e quindi è uniformemente
continua: per ogni δ > 0
esiste σ > 0
tale che
|(x,y) − (x′,y′)| < σ⇒|f(x,y) − f(x′,y′)| < δ.
La condizione
|(x,y) − (x′,y′)| < σ
vale in particolare se y = y′ ∈ [c,d]
e se |x − x′| < σ.
Dunque,
|x − x′| < σ⇒|f(x,s) − f(x′,s)| < δ⇒∫
cd f(x,s) − f(x′,s) ds < (d − c)δ.
L’assero segue scegliendo
δ = η
2(d − c).
Studiamo il secondo addendo (4.6). Per fissare le idee sia
y < y′:
|ϕ(x′,y) − ϕ(x′,y′)| = ∫
cyf(x′,s)ds −∫
cy′
f(x′,s)ds ≤∫
yy′
f(x′,s) ds.
La funzione f(x,y) è continua sul
rettangolo limitato e chiuso R.
Dunque, per il Teorema di Weierstrass, è limitata. Sia
|f(x,y)| < M. Per
la monotonia dell’integrale si ha
|ϕ(x′,y) − ϕ(x′,y′)|≤ M(y′− y).
Per avere questa differenza minore di
η∕2 basta imporre la
condizione |y′− y| < η∕2M. _
Di conseguenza, dal teorema sulla continuità delle funzioni composte, viene ad
essere continua anche la funzione
∫
cg(x,y)f(x,s)ds,
per ogni funzione continua g(x,y).
Scegliendo in particolare g(x,y)
costantemente uguale a b
si trova:
Teorema 140 Sia
f(x,y)
continua su
[a,b] × [c,d]
e sia
ϕ(x) = ∫
abf(x,y)dy.
La funzione ϕ(x)
è continua su [a,b].
Studiamo ora la derivabilità:
Teorema 141 Il rettangolo chiuso R
sia interno ad una regione Ω
su cui la funzione f(x,y)
ammette derivate parziali continue. Si ha:
|
∂
∂xϕ(x,y) = ∂
∂x∫
cyf(x,s)ds = ∫
cyf
x(x,s)ds
∂
∂yϕ(x,y) = ∂
∂y∫
cyf(x,s)ds = f(x,y).
|
Dim. La seconda uguaglianza è ovvia perchè il calcolo dell’integrale e quello della derivata parziale
rispetto ad y si
fanno per ogni x
fissata; e quindi di fatto si lavora con funzioni della sola variabile
y.
Proviamo la prima uguaglianza. Scriviamo
ϕ(x + h,y) − ϕ(x,y)
h −∫
cyf
x(x,s)ds = ∫
cy f(x + h,s) − f(x,s)
h − fx(x,s) ds.
Vogliamo provare che questa differenza tende a zero per
h → 0.
fissiamo s ∈ [c,d]
e scriviamo la formula della media per la funzione della sola variabiled
x:
f(x + h,s) − f(x,s)
h − fx(x,s) = fx(x̃,s) − fx(x,s)
ove x̃ dipende
sia da h che da
s. E’ però un punto
dell’intervallo (x,x + h). La funzione
fx(x,y) è uniformemente
continua su R e
quindi, dato 𝜖 > 0,
esiste δ𝜖 > 0
tale che
se |h| < δ𝜖 vale|fx(x̃,s) − fx(x,s)| < 𝜖;
e quindi,
ϕ(x + h,y) − ϕ(x,y)
h −∫
cyf
x(x,s)ds ≤∫
cy𝜖ds ≤ (d − c)𝜖.
Ciò prova che il limite per h
tendente a zero è nullo. _ Torniamo ora a considerare la funzione
ϕ(x) = ∫
cdf(x,y)dy.
Essendo questa funzione continua, essa può venir integrata rispetto alla variabile
x:
∫
ab ∫
cdf(x,y)dydx
Si chiama questo integrale iterato della funzione
f(x,y).
Naturalmente, si può anche introdurre un secondo integrale iterato,
∫
cd ∫
abf(x,y)dxdy
e si pone il problema di sapere se i loro valori coincidano o meno. La risposta
affermativa si vedrà nel cap. 7.
4.3 Le derivate di ordine superiore
Ricordiamo che le derivate parziali sono a loro volta funzioni di più variabili, e
quindi può accadere che esse siano ulteriormente derivabili. Si possono quindi
definire le funzioni
fxx(x,y) = ∂
∂x ∂
∂xf(x,y),fxy(x,y) = ∂
∂x ∂
∂yf(x,y)fyy(x,y) = ∂
∂y ∂
∂yf(x,y)
e cosìvia. Quando una funzione ammette tutte le derivate parziali continue fino all’ordine
k incluso su un
aperto Ω, si dice che
essa è di classe Ck(Ω).
La notazione
∂n
∂xnf(x,y)
indica la derivata n–ma
di f(x,y) rispetto
alla variabile x,
ossia la derivata ottenuta tenendo fisso il valore di
y e derivando
n volte
rispetto ad x.
Significato analogo ha il simbolo
∂n
∂ynf(x,y).
Le cose sono più complicate se si vogliono le derivate miste,
ossia le derivate ottenute derivando alcune volte rispetto ad
x e anche
rispetto ad y
perché in generale dovremo tener conto dell’ordine con cui si eseguono le derivate.
Per esempio, in generale
Dx Dyf(x,y) = ∂
∂x ∂
∂yf(x,y) ≠ ∂
∂y ∂
∂xf(x,y) = Dy Dxf(x,y) .
Fortunatamente, ciò non avviene nei casi più interessanti per le applicazioni.
Vale infatti:
Teorema 142 (di Schwarz) Sia f(x,y)
una funzione delle due variabili (x,y),
di classe C1
un intorno V
di (x0,y0).
Supponiamo che nei punti di V
esistano le derivate miste Dx Dyf(x,y)
ed Dy Dxf(x,y),
e supponiamo che queste siano continue. Allora, per ogni (x,y)
vale
Dx Dyf(x,y) = Dy Dxf(x,y) .
Esaminando la dimostrazione, in appendice, si vede facilmente che il teorema si estende al
caso di funzioni di più di due variabili. Grazie a questo teorema, le due derivate miste
rispetto ad x
ed y di
f(x,y) si
indicano semplicemente con i simboli
fx,y(x,y), ∂2
∂x∂yf(x,y),
senza preoccuparsi dell’ordine di derivazione. Il Teorema di Schwarz si estende a
funzioni di n
variabili, ed a qualsiasi ordine di derivazione, come segue:
Corollario 143 Sia f(r→) ∈ Cn(Ω).
Si derivi la funzione k1
volte rispetto alla prima componente di r→;
k2
rispetto alla seconda ecc., ma con
k1 + k2 + ⋯ + kn ≤ n.
La derivata che si ottiene non dipende dall’ordine col quale si eseguono le
derivate.
Indicare derivate successive di funzioni di più variabili è alquanto
noioso. Un simbolo comodo si ottiene in questo modo. Sia
f(r→) una funzione
di r→ ∈ ℝn. Chiamiamo
multiindice un vettore α = (α1,α2,…,αn)
le cui componenti sono numeri interi nulli o positivi. Indichiamo con
|α| la
lunghezza del multiindice:
|α| = α1 + α2 + α3 + ⋯ + αn.
Col simbolo r→α
intendiamo:
r→α = (r
1α1
,r2α2
,…,rnαn
).
Col simbolo
Dαf(r→) = ∂|α|
∂r→αf(r→)
si intende la derivata di f(r→) che si
ottiene derivando la funzione f(r→)
nell’ordine, prima α1 volte rispetto
alla prima variabile, poi α2
volte rispetto alla seconda variabile, ecc. (intendendo che se
αi = 0 la
corrispondente derivata non si esegue). Il Teorema di Schwarz assicura che se ciascuna derivata
di ordine |α| di
f(r→) è continua allora le
derivate miste di ordine |α|
non dipendono dall’ordine con cui vengono calcolate. Ciò giustifica la notazione
f ∈ Ck(Ω), che si usa quando la
funzione f(r→) ammette tutte
le derivate di ordine k
su Ω, e
queste sono continue.
4.3.1 La formula di Taylor per le funzioni a valori reali
Cosìcome nel caso delle funzioni di una variabile, gli argomenti che hanno condotto alla
prima formula degli incrementi finiti possono iterarsi se la funzione ammette continue le
successive N
derivate. Senza entrare nei dettagli della dimostrazione (simile a quella del
Teorema 132), limitiamoci a dare la formula che si ottiene nel caso delle
derivate seconde. Quando la funzione dipende da due variabili, si trova
|
f(x,y) = f(x0,y0)
+ fx(x0,y0)(x − x0) + fy(x0,y0)(y − y0)
+ 1
2 fxx(x0,y0)(x − x0)2 + f
xy(x0,y0)(x − x0)(y − y0)
+fyx(x0,y0)(x − x0)(y − y0) + fyy(x0,y0)(y − y0)2 + R(x,y).
|
e
|
lim d((x,y),(x0,y0))→0 R(x,y, )
[d((x,y), (x0,y0))]2 = 0,ossiaR(x,y) = o |(x − x0,y − y0)|2 .
| (4.7) |
Grazie al Teorema di Schwarz, la formula precedente si può scrivere
|
f(x,y) = f(x0,y0)
+ fx(x0,y0)(x − x0) + fy(x0,y0)(y − y0)
+ 1
2 fxx(x0,y0)(x − x0)2 + 2f
xy(x0,y0)(x − x0)(y − y0) + fyy(x0,y0)(y − y0)2
+ R(x,y).
|
Questa formula si chiama ancora formula di Taylor arrestata al secondo ordine perché il
resto R(x,y) verifica
la condizione (4.7). Naturalmente, aggiungendo i termini con le derivate rispetto ad una
terza variabile z
si trova la formula di Taylor in tre variabili e, in generale, in
n
variabili. Si immagina facilmente che le formule divengano via via
più complesse, in particolare se la funzione dipende da più di due
variabili e si vuole scrivere la formula di Taylor di ordine maggiore di
2.
E’ però possibile scrivere queste formule in modo compatto
come segue. Riguardiamo il caso della formula di Taylor di
f(x,y) arrestata
all’ordine 2.
Si noti che il termine
fx(x0,y0)(x − x0) + fy(x0,y0)(y − y0)
si può pensare ottenuto come segue:
1
1! (x − x0) ∂
∂x + (y − y0) ∂
∂yf(x,y) = 1
1! fx(x0,y0)(x − x0) + fy(x0,y0)(y − y0) .
Consideriamo ora il termine di ordine
2:
1
2 fxx(x0,y0)(x − x0)2 + 2f
xy(x0,y0)(x − x0)(y − y0) + fyy(x0,y0)(y − y0)2
si può ottenere con questa regola mnemonica: si “calcola”
1
2! (x − x0) ∂
∂x + (y − y0) ∂
∂y2
scrivendo
1
2! (x − x02) ∂2
∂x2 + 2(x − x0)(y − y0) ∂2
∂x∂y + (y − y02) ∂2
∂y2 .
Si “applica” quindi questo alla funzione
f(x,y)
scrivendo
|
1
2! (x − x02) ∂2
∂x2 + 2(x − x0)(y − y0) ∂2
∂x∂y + (y − y02) ∂2
∂y2 f(x,y)
= 1
2! (x − x0)2f
xx(x0,y0) + 2(x − x0)(y − y0)fxy(x0,y0) + (y − y0)2f
xx(x0,y0) .
|
Questa “regola mnemonica” si estende al caso dell’ordine maggiore di
2 e
fornisce l’espressione corretta della formula di Taylor arrestata all’ordine
k:
f(x,y) = ∑
j=0k 1
j! (x − x0) ∂
∂x + (y − y0) ∂
∂yjf(x,y)+o (x − x
0)2 + (y − y0)2 k.
In questa formula si intende che
(x − x0) ∂
∂x + (y − y0) ∂
∂y0f(x,y) = f(x
0,y0).
L’estensione di questa formula al caso di funzioni dipendenti da più di due
variabili è ovvia.
4.4 Gli estremi
La formula di Taylor, arrestata al primo ordine, ha già dato un’informazione
importante. Infatti, ha condotto a provare che ogni funzione le cui derivate parziali
sono ovunque continue è essa stessa continua. Daltra parte, nel caso delle funzioni
di una sola variabile, la formula di Taylor si usa per dedurre regole che
possono condurre ad identificare i punti di massimo o di minimo. Si può
immaginare che anche per funzioni di più variabili si possa fare uno studio
analogo. Per renderci conto di ciò, repetiamo la definizione degli estremi:
Definitione 2 Sia f(r→)
una funzione da ℝn → ℝ.
Un punto r→0
interno al dominio di f(r→)
si dice punto di minimo (relativo) per la funzione f(r→)
se esiste ν > 0
tale che
d(r→,r→0) < ν⇒f(r→0) ≤ f(r→).
In modo analogo si definiscono i punti di massimo. _
La figura 4.3 (a sinistra) mostra un punto di minimo.
Quando l’intorno di r→0
coincide con Ω, si
parla di estremi assoluti o estremi globali E naturalmente a questo caso ci si può ricondurre,
sostituendo Ω
con tale intorno. Studiamo ora il caso degli estremi relativi di
funzioni di due variabili, che sono interni al dominio. Notiamo che se
(x0,y0) è punto di minimo,
allora la funzione g(x)
della sola variabile x,
g(x) = f(x,y0)
ha minimo in x0
ed x0 è
punto interno al dominio. Dunque, se è derivabile, essa ha derivata nulla in
x0, per il Teorema di
Fermat. Per definizione, g′(x
0) = fx(x0,y0).
Se (x0,y0) è
punto di minimo, esso è anche punto di minimo per la funzione
h(y) = f(x0,y)
e quindi h′(y
0) = 0; e naturalmente
il discorso si ripete se (x0,y0) è
punto di massimo per f(x,y).
Dunque:
Teorema 144 Se la funzione
f(x,y)
ammette derivate parziali prime nel punto di minimo (o di massimo)
(x0,y0)
interno al dominio, esse sono ambedue nulle:
fx(x0,y0) = 0,fy(x0,y0) = 0.
Ossia: gli estremi di una funzione vanno ricercati tra i suoi punti stazionari. Naturalmente,
un punto stazionario, ossia un punto nel quale si annulla il gradiente della funzione,
non è necessariamente un estremo. Una coindizione suffciente per gli estremi si
vedrà più avanti. Però, in generale la funzione può avere un comportamente
quanto mai vario nei punti nei quali si annulla il gradiente. In particolare definiamo:
Definitione 3 Si dice che r→0
è punto di sella se è un punto stazionario e se, inoltre, la funzione f(r→) − f(r→0)
cambia segno in ogni intorno r→0. _
La figura 4.3, a destra, illustra un punto di sella. Dunque il piano tangente in un punto di
minimo o di massimo o di sella (interno al dominio) è orizzontale e, se la funzione è
di classe C2,
può scriversi:
|
f(x,y) = f(x0,y0) + 1
2 fxx(x0,y0)(x − x0)2
+2fxy(x0,y0)(x − x0)(y − y0) + fyy(x0,y0)(y − y0)2 + R(x,y)
|
con R(x,y)∕[(x − x0)2 + (y − y
0)2]
infinitesima. Per capire se è possibile ripetere, per le funzioni di più variabili, uno
studio analogo a quello delle funzioni di una variabile, consideriamo il caso particolare
in cui x0 = 0,
y0 = 0,
fxx(0, 0) = 1,
fxy(0, 0) = 0,
fyy(0, 0) = 1. In
questo caso,
|
f(x,y) = f(0, 0) + 1
2 fxx(0, 0)x2 + 2f
xy(0, 0)xy
+fyy(0, 0)y2 + R(x,y)
= f(0, 0) + (x2 + y2) ⋅1
2 + R(x,y)
x2 + y2.
|
Il teorema della permanenza del segno mostra che per
x2 + y2
abbastanza piccolo,
1 + 1
2 R(x,y)
x2 + y2 > 0
e quindi f(x,y)
ha, in (0, 0),
un punto di minimo relativo, cosìcome la funzione di confronto
g(x,y) = x2 + y2. In generale
se f(x,y) è di
classe C2
e le sue derivate prime sono ambedue nulle in un punto
(x0,y0) dalla
formula di Taylor si ha
f(x,y) = f(x0,y0) + g(x − x0,y − y0) + o(|(x − x0,y − y0)|2)
e la funzione di confronto g(x,y)
ha forma
g(x,y) = 1
2{fxx(x0,y0)(x−x0)2+2f
xy(x0,y0)(x−x0)(y−y0)+fyy(x0,y0)(y−y0)2}.
Le proprietà che il punto (x0,y0)
ha per le funzioni
g(x,y) = a(x − x0)2 + 2b(x − x
0)(y − y0) + c(y − y0)2
sono note dai corsi di geometria, caratterizzate mediante la matrice
H = ab b c .
Con una dimostrazione del tutto analoga a quella vista sopra in un
caso particolare, si prova: Se questa matrice è definita positiva, il
punto è di minimo; e tale proprietà è ereditada dalla funzione
f(x,y); se la
matrice è indefinita il punto è di sella, e tale proprietà è ereditata dalla funzione
f(x,y); se la matrice
è definita negativa, il punto è di massimo; e tale proprietà è ereditada dalla funzione
f(x,y). Se invece la
matrice è semidefinita positiva oppure semidefinita negativa, NIENTE PUÒ DIRSI SULLA
FUNZIONE f(x,y).
Ricordando i criteri introdotti nei corsi di geometria, per lo studio della definitezza
delle matrici, si ha:
- se a > 0
e det H > 0
la matrice H
è definita positiva, ed il punto è di minimo.
- se a < 0
e det H > 0
si ha un punto di minimo.
- se ac = 0
ma det H≠0
la matrice è indefinita ed il punto è di sella.
- se det H = 0
la funzione g(x,y)
ha per grafico un cilindro parabolico e niente può dirsi della funzione
f(x,y).
Questo risultato può estendersi a funzioni di
n
variabili. Introduciamo per questo la matrice hessiana della funzione
f(r→),
r→ = (x1,…,xn):
H(r→) = fx1,x1(r→)fx1,x2(r→)…fx1,xn(r→)
fx2,x1(r→)fx2,x2(r→)…fx2,xn(r→) ⋮
fxn,x1(r→)fxn,x2(r→)…fxn,xn(r→) .
Vale:
Teorema 145 Siano nulle le derivate parziali prime di
f(r→) in
r→0. In
tal caso:
- se la matrice hessiana è definita positiva, il punto è di minimo per
f(r→);
- se la matrice hessiana è indefinita il punto è di sella per f(r→);
- se la matrice hessiana è definita negativa, il punto è di massimo per
f(x,y).
Invece, NIENTE PUÒ DIRSI se la matrice hessiana è soltanto semidefinita positiva
oppure negativa.
Osservazione 146 E’ possibile dare ulteriori condizioni necessarie che devono
essere soddisfatte nei punti di minimo oppure di massimo. Ricordiamo che in un
punto di minimo r→0 = (x0,y0)
le derivate parziali prime devono essere tutte nulle. Questa condizione necessaria
si ottiene facilmente considerando la restrizione della funzione ad una delle
rette coordinate passanti per il punto; ossia, considerando la funzione f(x,y0)
si trova che deve essere fx(x0,y0) = 0.
Se esiste la derivata seconda, fxx(x0,y0)
non può essere negativa, altrimenti la funzione f(x,y0)
avrebbe in x0
un punto di massimo, invece che di minimo. Dunque, in un punto di minimo
(x0,y0)
si deve avere
fxx(x0,y0) ≥ 0,fyy(x0,y0) ≥ 0e quindi anche fxx(x0,y0) + fyy(x0,y0) ≥ 0.
In un punto di massimo deve aversi invece
fxx(x0,y0) ≤ 0,fyy(x0,y0) ≤ 0e quindi anche fxx(x0,y0) + fyy(x0,y0) ≤ 0.
Questa condizione si generalizza immediatamente al caso di funzioni
dipendenti da più variabili. Un’ulteriore condizione ancora solamente
necessaria ma più precisa è la seguente: In un punto di minimo le derivate
parziali prime sono nulle e inoltre la matrice hessiana è definita positiva oppure
semidefinita positiva. Infatti, se la matrice hessiana fosse definita negativa si
avrebbe un punto di massimo, se fosse indefinita si avrebbe un punto di
sella. Analogamente, In un punto di massimo le derivate parziali prime sono
nulle e inoltre la matrice hessiana è definita negativa oppure semidefinita
negativa. _
4.5 Il differenziale delle funzioni a valori in
ℝm
Sia F→(r→) una
funzione da ℝn
ad ℝm e sia
J→(r→) una trasformazione
lineare da ℝn ad
ℝm. Si dice che la
trasformazione lineare J→(r→)
è il differenziale di F→(r→)
in r→0
se
|F→(r→) −F→(r→0) −J→(r→ −r→0)| = o |r→ −r→0|.
Ovviamente, la i–ma
componente Fi(r→)
è una funzione a valori reali e dalla disuguaglianza
|Fi|≤|F→|seF→ = (F1,F2,…,Fm)
segue
|Fi(r→) − Fi(r→
0) − Ji(r→ −r→
0)| = o(|r→ −r→0|).
ove Ji(r→) è la
i–ma componente
di J→(r→). Segue che
una funzione da ℝn
in ℝm che
è differenziabile ha differenziabile, e quindi continua, ciascuna delle sue
componenti:
Teorema 147 Se la funzione F→(r→)
è differenziabile in r→0,
essa è ivi continua.
Viceversa, dalle disuguaglianze (3.3), esiste un
M per
cui
|F→(r→)−F→(r→0)−J→(r→−r→0)|≤ M∑
i=1m|Fi(r→)−Fi(r→
0)−Ji(r→−r→
0)|.
Dunque:
Teorema 148 La funzione
F→(r→)
è differenziabile in
r→0
se e solo se ciascuna delle sue componenti lo è.
Ricordiamo che le trasformazioni lineari da
ℝn ad
ℝm (che
rappresentiamo rispetto alle basi canoniche) si rappresentano mediante matrici. Sia
J la matrice della
trasformazione lineare J→(r→),
differenziale in r→0
della funzione F→(r→).
La sua i–ma
riga rappresenta il differenziale della componente
Fi(r→)
e quindi è il trasposto del gradiente della funzione
Fi(r→); e
quindi
J(r→0) = ∂
∂x1F1(r→
0) ∂
∂x2F1(r→
0) … ∂
∂xnF1(r→
0)
∂
∂x1F2(r→
0) ∂
∂x2F2(r→
0) … ∂
∂xnF2(r→
0) ⋮
∂
∂x1Fm(r→
0) ∂
∂x2Fm(r→
0)… ∂
∂xnFm(r→
0)
La matrice J
si chiama la matrice jacobiana della funzione
F→(r→), calcolata
in r→0.
Quando n = m,
il suo determinante si chiamo lo jacobiano della trasformazione. Per mezzo della
matrice jacobiana, possiamo scrivere
|
F→(r→) = F→(r→0) + J(r→0)(r→ −r→0) + o(|r→ −r→0|).
| (4.8) |
Quest’uguaglianza si chiama ancora formula degli incrementi finiti. Ovviamente,
lavorando per componenti, si potrà scrivere anche una formula di Taylor per funzioni
da ℝn in
ℝm,
su cui non indugiamo. Come nel caso delle funzioni a valori in
ℝ, la
sola esistenza delle derivate parziali non implica né la continuità né la
differenziabilità; ma la continuità delle derivate parziali in un insieme aperto
implica la differenziabilità, su tale insieme, di ciascuna delle componenti
Fi(r→) e quindi
di F→(r→),
ossia:
Teorema 149 Le derivate parziali ∂
∂xiFj(r→
0)
per 1 ≤ i ≤ n,
1 ≤ j ≤ m
esistano continue in un intorno di r→0.
Allora, la funzione F→(r→)
è differenziabile e quindi continua in r→0.
Rappresentiamo ℝn rispetto alla
base canonica e sia J una
trasformazione lineare di ℝn in
sé. Col medesimo simbolo J
indichiamo anche la matrice che rappresenta la trasformazione. Si sa che la trasformazione
J trasforma un
parallelepipedo in un altro e l’area del secondo è uguale all’area del primo moltiplicata
per | det J|.
Consideriamo ora una trasformazione differenziabile da
ℝ2 in
sé:
x = x(u,v),y = y(u,v).
fissiamo un punto r→0 = (u0,v0)
ed un rettangolo R
con un vertice in r→0.
L’immagine di R
è
x(u,v) y(u, v)
, (u,v) ∈ R = x(u0,v0)
y(u0,v0) + J u − u0
v − v0 + o→ u − u0
v − v0
ove J
indica la matrice jacobiana della trasformazione. Quest’insieme non è un
rettangolo. E’ un insieme dalla struttura più complicata, ma approssimato dal
parallelogramma
R̃ = x(u0,v0)
y(u0,v0) + J u − u0
v − v0 .
Dal paragrafo 3.5
(area di R̃) = det J ⋅(area di R).
Asserto analogo vale per le trasformazioni di
ℝ3.
Quest’osservazione verrà utilizzata nel paragrafo 7.3.1.
Esempio 150 La figura 4.4 riporta, a sinistra, il rettangolo
R = [1, 2] × [1, 3∕2]
del piano
(u,v)
e a destra la sua immagine mediante la trasformazione
x = u + (uv)2,y = v2 + uv.
Il parallelogramma a destra è R̃.
Osservazione 151 Si vede dalla formula degli incrementi finiti che la matrice
jacobiana ha, nel caso delle funzioni da ℝn
in ℝm,
lo stesso ruolo che la derivata ha nel caso n = m = 1.
Per questa ragione la matrice jacobiana talvolta si indica anche col simbolo
∂F→(r→)
∂r→ .
Per esempio, nel caso n = m = 2
e F→(x,y) = f(x,y)g(x,y) ′,
la matrice jacobiana si trova anche indicata con la notazione
∂ f(x,y),g(x,y)
∂(x,y) .
Osservazione 152 (Sulle notazioni) Non esiste una notazione standard
per lo jacobiano o per la matrice jacobiana. Nei testi di meccanica del continuo
e di scienza delle costruzioni lo jacobiano viene indicato col simbolo ∇,
come il gradiente. Si faccia attenzione però che se lo spazio d’arrivo ha
dimensione 1
allora ∇=“grad”
indica un vettore colonna mentre ∇=“matrice
jacobiana” indica un vettore riga.
Si faccia anche attenzione a questo: nei testi di meccanica del continuo si
considerano funzioni u→ = u→(X→,t)
con X→
e u→
in ℝ3
e t ∈ ℝ.
La notazione ∇u→ = ∇u→(X→,t)
indica la matrice jacobiana fatta rispetto al vettore X→,
ossia
∇u→(X→,t) = ∂u1(X1,X2,X3,t)
∂X1 ∂u1(X1,X2,X3,t)
∂X2 ∂u1(X1,X2,X3,t)
∂X3
∂u2(X1,X2,X3,t)
∂X1 ∂u2(X1,X2,X3,t)
∂X2 ∂u2(X1,X2,X3,t)
∂X3
∂u3(X1,X2,X3,t)
∂X1 ∂u3(X1,X2,X3,t)
∂X2 ∂u3(X1,X2,X3,t)
∂X3
.
I testi di meccanica del continuo usano una notazione interessante per le
derivate: le derivate si indicano con indici numerici preceduti da virgola. Per
esempio, sia
u→(x1,x2,x3) = u1(x1,x2,x3)u2(x1,x2,x3)u3(x1,x2,x3) ′.
Il simbolo
u→i,j
indica la derivata rispetto ad xj
della componente ui;
ossia il numero prima della virgola specifica la componente e quello dopo
specifica la variabile rispetto a cui si deriva. Questo simbolo si può iterare e
per esempio
u→2,13 = ∂2
∂x1∂x3u2(x1,x2,x3).
4.5.1 Regole di calcolo della matrice jacobiana
Usiamo il simbolo JF→(r→)
per indicare la matrice jacobiana della funzione
F→ nel
punto r→.
E’ immediatamente evidente che
|
JAF→(r→) = AJF→(r→)per ogni matrice costante A;
JF→+G→(r→) = JF→(r→) + JG→(r→).
|
Supponiamo ora di esprimere r→ ∈ ℝn
come funzione
r→ = r→(u→),u→ ∈ ℝk.
Vale
Teorema 153 (della derivazione a catena) Sia F→(r→)
di classe C1
in una regione Ω
di ℝn;
r→(u→)
sia di classe C1
in una regione Ω ̃ ⊆ ℝk,
ed a valori in Ω.
Sia G→(u→) = F→(r→(u→)).
Si ha
JG→(u→0) = JF→(r→(u→0))Jr→(u→0).
Il prodotto tra matrici si intende come prodotto righe per colonne.
Omettiamo la dimostrazione.
4.6 Campi vettoriali
Nel trattare le funzioni a valori vettoriali, abbiamo sempre specificato “a valori in
ℝm ”. Si
ricordi che ℝm
è uno spazio di vettori liberi, equivalentemente, applicati nell’origine. In
molte applicazioni si devono considerare funzioni che associano ad un punto
r→ di
ℝn un vettore
ad n
dimensioni, applicato nel punto stesso. Ossia si devono studiare trasformazioni che
trasformano r→
nella coppia (r→,V →(r→)).
Trasformazioni di questo tipo si chiamano campi vettoriali. E’ comune usare la lettera
V → per indicare campi
vettoriali. Si scrive cioè V →(r→)
sottintendendo che questo vettore è applicato in
r→,
invece di scrivere la notazione completa, ma pedante,
(r→,V →(r→)) La
figura 4.5 illustra il modo con cui usualmente si rappresentano i campi vettoriali:
da ciascun punto si fa uscire una freccia che indica direzione e verso del vettore.
La lunghezza della freccia è proporzionale al modulo. Quando si lavora
con campi vettoriali, i concetti di continuità e di differenziabilità sono
concettualmente diversi da quelli incontrati per i vettori liberi, perché non si
fanno operazioni tra vettori applicati in punti diversi. Per questo la definizione
di continuità di un campo vettoriale si definisce confrontando il vettore
V →(r→), applicato in
r→ col vettore
PARALLELO a V →(r→′),
anch’esso applicato in r→
invece che in r→′.
Fortunatamente, la somma di vettori applicati nel medesimo punto si
fa operando per componenti, e queste non mutano per spostamenti per
parallelismo. Si ha quindi che un campo vettoriale è continuo se e solo se sono
continue le sue componenti. Discorso analogo vale per le derivate. Si fissi
r→0 ed un vettore
libero v→.
Si considerino i vettori
r→0 + tv→
che sono i vettori di una retta parallela a
v→, passante per
r→0. Si chiama derivata
secondo il vettore v→
il limite
Dv→V →(r→0) = lim t→0V →(r→0 + tv→) −V →(r→0)
t .
La differenza al numeratore si calcola supponendo di traslare per parallelismo il vettore
V →(r→0 + tv→) applicandolo nel
punto r→0. Dunque,
anche il vettore Dv→V →(r→0)
è applicato in r→0.
Se v→ è il
versore e→i,
tale derivata si chiama anche derivata direzionale. Il teorema di derivazione della
funzione composta immediatamente dà:
Teorema 154 Sia V →(r→)
un campo vettoriale le cui componenti sono funzioni di classe
C1. Esso
ammette derivate direzionali in tutte le direzioni, e vale
|
Dv→V →(r→0) = JV →(r→0)v→
| (4.9) |
In questo teorema, il simbolo JV →(r→0)
indica la matrice jacobiana della trasformazione che al vettore libero
r→ associa il vettore
libero V →(r→). Il vettore
Dv→V →(r→0) si intende
applicato in r→0.
4.6.1 Operatori differenziali e campi vettoriali
Abbiamo visto che il gradiente di una funzione a valori scalari è il vettore
∇f(r→) = fx1(r→)
fx2(r→) ⋮
fxn(r→) .
Per molte applicazioni, conviene considerare questo un vettore applicato nel punto
r→.
Dunque il gradiente associa un campo vettoriale ad una funzione a valori scalari. Si
noti che
∇u→f(r→(u→)) ′ = ∇
r→f(r→(u→)) ′J
r→[u→]
ove
l’apice indica la trasposizione e l’indice sotto il simbolo
∇
indica le variabili rispetto alle quali si calcola il gradiente.
Introduciamo una notazione comoda: sia {e→1,…,e→n}
la base canonica di ℝn.
Scriviamo in modo formale
|
∇ =e→1 ∂
∂x1 + e→2 ∂
∂x2 + ⋯ + e→n ∂
∂xn
=e→1∂1 + e→2∂2 + ⋯ + e→n∂n
= ∂1
∂2
⋮ ∂
n .
|
Allora il gradiente si ottiene formalmente “moltiplicando” il “vettore”
∇ per lo
“scalare” f(r→),
e eseguendo le operazioni di derivazione. Introdotto il simbolo
∇, viene
naturale introdurre le operazioni
∇⋅V →(r→),∇∧V →(r→)
operando formalmente come se si trattasse di prodotti scalari o vettoriali (e quindi la seconda si
definisce solo in ℝ3).
La prima dà la divergenza del campo vettoriale:
divV →(r→) = ∂
∂x1V 1(r→) + ∂
∂x2V 2(r→) + ⋯ + ∂
∂xnV n(r→).
Il risultato della seconda operazione, DEfiNITA SOLO IN
ℝ3, si
chiama rotore: il rotore del campo vettoriale
V →(x,y,z) = u(x,y,z)i→ + v(x,y,z)j→ + w(x,y,z)k→
è quindi (sottintendendo le variabili indipendenti) il campo vettoriale
rotV → = ∇∧V → = (wy − vz)i→ + (uz − wx)j→ + (vx − uy)k→.
Si noti che, sviluppando formalmente secondo gli elementi della prima
riga,
rotV → = i→j→k→
∂
∂x ∂
∂y ∂
∂z
u v w .
Sia ora u(x,y,z)
una funzione due volte derivabile. Calcoliamo prima il gradiente di
u(x,y,z) e poi
la divergenza del gradiente:
∇⋅ (∇u(x,y,z)) = uxx(x,y,z) + uyy(x,y,z) + uzz(x,y,z).
Usa definire Δ,
che si chiama laplaciano, ponendo
Δu(x,y,z) = uxx(x,y,z) + uyy(x,y,z) + uzz(x,y,z).
Formalmente si scrive
Δ = ∇⋅∇.
Si vede facilmente che queste considerazioni valgono per funzioni di qualunque
numero di variabili.
Osservazione 155 (Sulle notazioni) Proseguiamo quanto si è detto all’osservazione 152.
Facendo intervenire le notazioni dei campi vettoriali, i testi di meccanica
del continuo e di scienza delle costruzioni scrivono la prima formula degli
incrementi finiti in questo modo. Sia u→(x→)
una funzione di tre variabili a valori in ℝ3.
Usando la notazione “con la virgola” introdotta all’osservazione 152, la prima
formula degli incrementi finiti è
u→(x→) = u→(0 →)+ u1,1(0 →)u1,2(0 →)u1,3(0 →)
u2,1(0 →)u2,2(0 →)u2,3(0 →)
u3,1(0 →)u3,2(0 →)u3,3(0 →) x1
x2
x3 +o(||x→||).
Invece di scrivere in questo modo, viene scritto:
u→(x→) = u→(0 →) + x→ ⋅∇u→(0 →) + o(||x→||)
ove x→ ⋅∇
indica un “prodotto scalare formale” tre i due vettori colonna x→
e ∇,
x→⋅∇ = x1
x2
x3 ⋅∂1
∂2
∂3 = x1∂1+x2∂2+x3∂3.
Si trova quindi un operatore differenziale che si applica al campo vettoriale
u→(x→),
applicandolo a ciascuna delle sue componenti:
|
x→ ⋅∇u→(x→) = x1
x2
x3 ⋅∂1
∂2
∂3 u→(x→)
= x1∂1 + x2∂2 + x3∂3 u→(x→) = x1u1,1 + x2u1,2 + x3u1,3
x1u2,1 + x2u2,2 + x3u2,3
x1u3,1 + x2u3,2 + x3u3,3
|
proprio come si voleva ottenere. _
4.7 Appendici
4.7.1 Appendice: Rappresentazione di funzioni di due variabile
In quest’appendice mostriamo alcune funzioni di due variabili a valori reali, ed il
modo di rappresentarle. Sostanzialmente, ci sono tre modi. Descriviamoli
prima di tutto in astratto e poi illustriamoli su opportuni esempi. Sia
f(x,y) una
funzione. Il modo più ovvio di rappresentarla consiste nel costruirne il grafico,
ossia nel costruire l’insieme
{(x,y,z)|z = f(x,y)}⊆ ℝ3.
Naturalmente questo richiede la costruzione di un modello per esempio di gesso o
di plastica. In pratica rappresenteremo il grafico su un foglio, mediante opportune
tecniche di disegno, che diano l’illusione della profondità. Inoltre, talvolta
conviene rappresentare, invece della superficie, solamente una famiglia di linee
sulla superficie. Il secondo metodo consiste nel tagliare il grafico a quota
c,
e quindi nel proiettare l’insieme intersezione sul piano
(x,y). Si disegna
cioè sul piano (x,y),
l’insieme delle soluzioni dell’equazione
f(x,y) = c.
Quest’insieme si chiama insieme di livello In molti
casi
un insieme di livello è una “curva” e quindi si parla di curva di livello Disegnando
“numerose” curve di livello si può avere un’informazione sul comportamento
della funzione: per esempio, le curve di livello sono più fitte dove il grafico
della funzione è più ripido. Il terzo metodo consiste nel colorare il piano
(x,y)
colorandolo con colori “freddi”, per esempio blu, dove i valori della funzione
sono più piccoli e con colori caldi, per esempio rosso, dove la funzione
prende valori maggiori. Molto spesso conviene combinare questi metodi,
attribuendo i colori alla superficie o alle sue curve di livello. Vediamo ora un
esempio. Consideriamo la funzione seguente, il cui grafico è un paraboloide di
rotazione:
f(x,y) = x2 + y2.
La figura 4.6 mostra vari modi di rappresentare il grafico di questa funzione.
La figura 4.7 mostra a sinistra la funzione rappresentata mediante le
sue curve di livello (e quindi mediante una rappresentazione sul piano
(x,y)) ed a
destra il grafico (fatto con fili) della medesima funzione, sovrapposto alle curve di
livello.
Ciò detto, passiamo ad esaminare alcuni esempi di funzioni.
Funzioni costanti rispetto ad una variabile Può accadere che una funzione
f(x,y) sia “costante
rispetto ad y”;
ossia che valga
f(x,y) = f(x,y′)
per ogni scelta di y
e di y′,
purché la x
prenda il medesimo valore a destra ed a sinistra. Vediamo le conseguenze “grafiche”
di questa proprietà. La funzione è costante sulle rette verticali del piano
(x,y), che
pertanto sono tutte contenute in insiemi di livello. Per esempio la funzione
ha gli insiemi di livello rappresentati nella figura 4.8 a sinistra.
Rette del medesimo colore corrispondono al medesimo livello e quindi
gli insiemi di livello in quest’esempio non sono “curve”, ma sono insiemi
di (infinite) rette verticali. Dal punto di vista del grafico, il grafico della
funzione è unione di rette orizzontali, e quindi tutte parallele tra loro. Il
termine superficie verrà introdotto più avanti, ma è un fatto che sono
“superfici” i grafici di funzioni (differenziabili). Una superficie che è unione di
rette tutte tra loro parallele si chiama cilindro Dunque, i grafici di funzioni
f(x,y)
costanti rispetto ad una variabile sono cilindri. Il cilindro corrispondente alla
funzione in esame è nella figura (4.8), a destra.
Funzioni omogenee Si chiamano funzioni omogenee di grado
ν (non
necessariamente intero) quelle funzioni che verificano l’uguaglianza
f(rx,ry) = |r|νf(x,y).
Se ν = 0 la
funzione è costante sulle rette che escono dall’origine, che pertanto appartengono
ad insiemi di livello. Un esempio è la funzione
f(x,y) = x2 − y2
x2 + y2.
Dato che il denominatore si annulla in
(0, 0),
per evitare diffcoltà di tipo numerico, consideriamola nel quadrati
0, 1 ≤ x ≤ 1,
0, 1 ≤ y ≤ 1.
La figura 4.9, a sinistra, presenta le curve di livello della funzione. Come
si è detto, queste sono rette, ma problemi di tipo numerico vicino a
(0, 0)
(dove si annullano sia il numeratore che il denominatore) provocano le
distorsioni visibili in figura. Il valore della funzione varia da retta a retta,
ma rimane costante sulle singole rette, come mostra la figura 4.9, a
destra. In questa figura abbiamo rappresentato, in verde, anche il piano
z = 0.
Se la funzione è omogenea di grado
1 allora
moltiplicando per r
sia x che
y, il valore di
z viene anch’esso
moltiplicato per r.
Dunque, se un punto (x0,y0,z0) è
sul grafico, anche i punti (rx0,ry0,rz0)
con r > 0 sono sul grafico.
Al variare di r,
questi descrivono semirette passanti per l’origine: il grafico è unione di
semirette passanti per l’origine. Un insieme unione di rette per un medesimo
punto si chiama cono E quindi il grafico di una funzione omogenea di grado
1 è un
semicono (con vertice nell’origine). La figura 4.10, a sinistra, illustra la situazione
nel caso della funzione
f(x,y) = xy
x + y.
La figura riporta sia il grafico della funzione sia alcune rette che escono dall’origine
e che appartengono al grafico. La figura 4.10, a destra, riporta invece il grafico della
funzione
f(x,y) = xy
x + y,
omogenea di grado 1∕2.
La figura riporta anche una retta per l’origine e per un punto del grafico che, come
si vede, non giace sul grafico.
Simmetrie del grafico, funzioni radiali e superfici di rotazione Il grafico
di una funzione di più variabili può avere proprietà di simmetria, che estendono
quelle note per le funzioni di una variable. Per esempio, diremo che una funzione
f(x,y) è
- dispari se f(x,y) = −f(−x,−y);
- pari se f(x,y) = f(−x,−y).
Come nel caso delle funzioni di una variabile, queste proprietà corrispondono a certe
simmetrie del grafico rispetto all’origine. Naturalmente, si possono avere altre
possibilità che non si incontrano nel caso di funzioni di una variabile (per esempio,
simmetrie rispetto ad una retta per l’origine, magari ad uno degli assi coordinati).
A noi ora interessa un caso molto particolare di funzione pari di due variabili,
ottenuta a partire da funzioni di una sola variabile. Si consideri la funzione
t↦f(t) di una sola variabile
definita su un intervallo
[a,b] e a
questa si associ la funzione di due variabili
(x,y)↦f x2 + y2
ossia la funzione
z = f x2 + y2 ,domf = (x,y),x2 + y2 ∈ [a,b] .
I grafici di queste funzioni hanno una proprietà particolare. Sia
(x0,y0) ∈ domf x2 + y2 edr0 = x0 2 + y0 2.
Il numero r0 è la
distanza di (x0,y0) dall’origine.
Qualunque altro punto (x,y)
che dista r0
dall’origine, ossia per cui
x2 + y2 = r0
appartiene al dominio della funzione ed inoltre,
f x2 + y2 = f x0 2 + y0 2 .
Dunque il dominio della funzione è una
corona circolare di centro l’origine (un disco se
a = 0,
l’esterno di un disco se a > 0
ed r = +∞),
e tutte le circonferenze di centro l’origine sono curve di
livello della funzione. Questo si interpreta in questo modo:
se il dominio della funzione contiene un punto
P,
esso contiene tutta la circonferenza di centro
O
che passa per P.
Inoltre su tale circonferenza la funzione è costante. Ossia se il punto
P
ruota su una circonferenza di centro
O
il corrispondente punto del grafico ruota
su una circonferenza parallela al piano
x,y,
centrata sull’asse delle quote. Detto in altro modo, ogni
piano perpendicolare all’asse delle quote se interseca il
grafico della funzione lo interseca lungo una circonferenza
(oppure in un solo punto). Una superficie come quella ora
descritta si chiama superficie di rotazione. L’intersezione tra un piano
z = z0
e il grafico, se non è vuota, si chiama un parallelo della superficie mentre
l’intersezione tra il grafico ed ogni piano passante per l’asse delle quote si
chiama meridiano della superficie di rotazione: la superficie di rotazione
può anche pensarsi ottenuta ruotando un meridiano intorno
all’asse delle quote. Il grafico nella figura 4.11 mostra una superficie di
rotazione, con indicati alcuni paralleli ed alcuni meridiani.
Funzioni periodiche Una funzione di due variabili,
f(x,y), si dice periodica
quando esiste un vettore v→0 = (ξ0,η0)
tale che
f(x→) = f(x + ξ0,y + η0) = f(x,y)
per ogni (x,y)
del suo dominio. Un esempio è la funzione
f(x,y) = (sin x)(sin 2 ∗ y).
Se
v→ = 2πi→ + πj→
si ha
f(x→ + v→) = f(x + 2π,y + π) = sin(x + 2pi) sin 2(y + π) = f(x,y).
La figura 4.12 mette a confronto il grafico della funzione
f(x,y), a
sinistra, con le sue curve di livello, a destra.
4.7.2 Appendice: Propagazione ondosa
In molte applicazioni si incontrano funzioni della forma
f(ϕ(x→) − vt)oppuref(ϕ(x→) + vt)
con v > 0. In queste
applicazioni la variabile t
si interpreta come “tempo” mentre la variabile
x→
indica una posizione nello spazio. Dunque la funzione
f(ϕ(x→) ± vt) descrive una
configurazione f(ϕ(x→))
che “si muove” al passare del tempo e ciò suggerisce un
linguaggio particolare, che illustriamo con riferimento al caso
x→ = x ∈ ℝ e
ϕ(x) = x oppure
ϕ(x) = mx. In queste applicazioni,
la funzione f(x)
si chiama onda Potremmo pensare al suo grafico come alla configurazione all’istante
t = 0 di un
corpo elastico. Vediamo come si interpetano le due funzioni
F1(x,t) = f(x − vt),F2(x,t) = f(x + vt)
con v > 0. Consideriamo
la funzione F1(x,t).
fissiamo un valore t0.
La funzione x → f(x − vt0)
si può interpretare in due modi diversi: come la funzione
f(x) rappresentata
rispetto ad un sistema di riferimento ottenuto traslando l’origine nella posizione
−vt0 dell’asse
x. Dunque in
dietro, perché v > 0.
Questo modo di intendere le cose è il più comune nelle applicazioni
geometriche. Invece, nelle applicazioni fisiche e nell’analisi si
incontra più frequentemente un’interpretazione diversa: si pensa ad
f(x) ed
f(x − vt0)
come a due diverse funzioni rappresentate rispetto al medesimo
sistema di riferimento. In tal caso, il grafico della funzione
f(x − vt0) è ottenuto traslando
in avanti il grafico di f(x).
Se t si
interpreta come “tempo”, nell’unità di tempo il grafico è andato avanti di una
quantità v.
Dunque, v
rappresenta la velocità dello spostamente del grafico. Pensando al grafico di
f(x) come ad un’“onda”,
si dice che v
è la velocità di propagazione dell’onda. Le stesse considerazioni si possono ripetere per la
funzione F2(x,t)
con la sola differenza che ora il grafico si sposta in dietro (grazie al fatto che
v si è
scelto positivo). Le considerazioni precedenti suggeriscono di chiamare la funzione
F1(x,t) = f(x − vt) onda progressiva mentre
la funzione F1(x,t) = f(x + vt) si chiama onda
regressiva (ricordiamo che v > 0).
La figura 4.13 riporta i grafici delle funzioni
a sinistra sono riportati i grafici delle funzioni
x → e−(x+t)2 nel medesimo sistema
di assi cartesiani (x,y),
per diversi valori di t.
A destra è stato costruito il grafico della funzione di due variabili
(x,t) → e−(x+t)2, nello spazio riferito
agli assi cartesiani (x,t,z).
Questo grafico è stato sezionato con i piani
t = 0,
t = 2,
t = 3 e
t = 4, e
sono stati disegnati i grafici risultanti da queste sezioni.
Il termine “onda” o “moto ondoso” usato per descrivere la situazione
illustrata sopra è particolarmente intuitivo nel caso di funzioni
f(x)
periodiche. La figura 4.14 riporta grafici analoghi a quelli della figura 4.13, ma
questa volta con la funzione
Si noti che questa funzione è periodica di periodo
2π∕m. Il valore scelto nella
figura per il periodo è 3.
Il caso in cui f(x) = sin(mx)
oppure f(x) = cos(mx) è
particolarmente importante nelle applicazioni. Le “onde” costruite a partire da queste
funzioni si dicono onde armoniche e in questo caso si usano notazioni e definizioni
peculiari che verranno illustrate al paragrafo 4.7.2. Consideriamo ora la funzione
F1(x,t) = f(x − vt). Questa funzione
prende il valore f(k)
in tutti i punti (x,t)
nei quali
x − vt = k.
Per ogni k
si viene cosìa descrivere una retta nei punti della quale l’onda ha il
medesimo valore. Ciò suggerisce di dare un nome alla quantità
x − vt: questa si
chiama la fase dell’onda progressiva. Al trascorrere del tempo, si rimane sulla stessa fase
k se si passa dal
punto x al punto
x + vt, ossia se si sposta il punto
osservato x in avanti con
velocità v. Per questa
ragione, il numero v
si chiama anche (e più frequentemente) velocità di fase Considerazioni analoghe
per le onde regressive si lasciano per esercizio. Si noti che talvolta un’onda viene
scritta come
f(hx − mt) = f h(x − (m∕h)t) .
In tal caso, la velocità di fase è v = m∕h.
Se x→ ∈ ℝ2
oppure x→ ∈ ℝ3
si incontra un nuovo concetto, che illustriamo con riferimento a
x→ ∈ ℝ2,
x→ = xy ′.
Consideriamo le due onde progressive seguenti:
Φ1(x→,t) = Φ1(x,y,t) = f(ax+by−vt),Φ2(x→,t) = Φ2(x,y,t) = f x2 + y2 − vt.
Ci si può chiedere su quali insiemi del piano
(x,y)
l’onda ha la medesima fase per ogni fissato valore di
t. Lavorando con
la funzione Φ(x→,t),
fissato t = t0, la
fase vale k
nei punti della retta
ax + by = k + vt0;
nel caso della funzione Φ2(x→,t)
fissato t = t0, la
fase vale k
nei punti della circonferenza
x2 + y2 = k + vt
0.
Per questa ragione, l’onda Φ1(x→,t) si
chiama onda piana mentre l’onda Φ2(x→,t)
si chiama onda sferica
Onde e moto armonico
Ricordiamo che si chiama moto armonico il moto di un punto lungo una circonferenza,
se questo avviene con velocità angolare costante. I punti di una circonferenza di
raggio A
hanno coordinate
|
A cos(ωt + ϕ),A sin(ωt + ϕ) .
| (4.13) |
Il numero (2π)∕ω
è il tempo necessario a descrivere una volta tutta la circonferenza e quindi
T = 2π
ω
è il periodo del moto mentre il suo reciproco
f = ω
2π
si chiama frequenza del moto. La frequenza indica quanti giri (o parti di
giro) percorre il corpo lungo la circonferenza in un’unità di tempo. Il
numero di radianti di cui varia la posizione del corpo nell’unità di tempo è
ω e per questo
il coeffciente ω
si chiama velocità angolare Dunque,
ω = 2πf.
Dato che ω = (2π)∕T,
la (4.13) si può anche scrivere (si confronti con l’osservazione 82 dove però il
periodo è 2T)
A cos 2π
T t,A sin 2π
T t.
Questo legame col moto armonico suggerisce di chiamare onde armoniche le
onde
A cos(kx − ωt + ϕ),A sin(kx − ωt + ϕ)
(e le analoghe onde regressive, il cui esame si lascia per esercizio). Consideriamo
per fissare le idee l’onda progressiva
A sin(kx − ωt + ϕ).
Il numero A si chiama l’ampiezza
dell’onda e il numero kx − ωt + ϕ
si chiama la fase Le due onde
A sin(kx − ωt + ϕ),A sin(kx − ωt + ψ)
(con gli stessi valori di ω
e di k) si dicono
sfasate di ϕ − ψ
e questo numero si chiama sfasamento tra le due
onde. Per semplicità di
scrittura, poniamo ora ϕ = 0.
L’onda che si trova all’istante t = 0
è l’onda
f(x) = sin kx,
periodica di periodo 2π∕k.
Però, i fisici riservano i termini “periodo” e “frequenza” alla variabile tempo. Il
numero
λ = 2π
k
si chiama invece lunghezza d’onda Infatti, l’onda prende i medesimi valori nei punti che distano
l’uno dall’altro di 2π∕k.
Questo può visualizzarsi in questo modo: consideriamo la funzione
fe(x) = sin kx,x ∈ [0, 2π∕k) = [0,λ).
chiamiamola “onda
elementare”. Allora il grafico di f(x)
si può pensare ottenuto giustapponendo i grafici di
fe(x + n(2π∕k)) per ogni
numero intero n.
La figura 4.15 illustra ciò, usando colori diversi per vedere i grafici che si sono
giustapposti.
Il numero di onde elementari che si ripetono nell’unità di spazio è
1
diviso per la lunghezza dell’onda elementare, che è
k∕2π. Il
valore
1
λ = k
2π
si chiama numero d’onde mentre k
si chiama numero d’onde angolare Come si è detto, i termini “periodo”,
“frequenza” e “freqenza angolare” si riservano alla dipendenza dal tempo
t
dell’onda. Ossia, si riservano alla funzione
t → A sin(kx − ωt + ϕ)
con x fissato.
La terminologia è quella già illustrata nel contesto del moto armonico. Indicando
con T il
periodo, si ha
T = 2π
ω ,f = 1
T = ω
2π
Il numero ω,
che è la velocità angolare del moto armonico, nello studio delle onde
armoniche si chiama frequenza angolare Studiamo infine la velocità di fase,
scrivendo
sin(ωt + kx) = sin k ω
kt + x.
La velocità di fase, ossia la velocità di spostamento dell’onda, è
v = ω
k = λ
T.
Onde stazionarie
Le onde si “propagano” nello spazio, al trascorrere del tempo; questa almeno
sembra l’informazione che può ricavarsi dalle considerazioni precedenti. Però, in
uno stesso mezzo possono propagarsi onde diverse. Consideriamo due onde
armoniche con la medesima ampiezza
f(x − vt) = A cos k(x − vt),g(x − vt) = A cos m(x − νt).
Se le due onde hanno il medesimo numero d’onde,
k = m e la medesima
velocità, v = ν,
allora nel mezzo si vede un’onda di ampiezza doppia,
2A cos(kx − vt).
Altrimenti, si trova la funzione
(x,t)→A cos k(x − vt) + cos m(x − νt) .
Usando le formule di prostaferesi si trova la funzione
|
2A cos (k + m)x − (kv + mν)t
2 cos (k − m)x + (mν − kv)t
2
= 2A cos k + m
2 x −kv + mν
k + m t cos k − m
2 x + mν − kv
k − m t
|
Supponiamo ora che la velocità di propagazione sia uguale per le due onde,
v = ν. In
questo caso si trova il segnale
2A cos k − m
2 (x − vt) cos k + m
2 (x − vt)
Interpretiamo questa formula: quando i due segnali hanno numero d’onde molto simile,
k ∼ m e “molto grande”, allora
𝜖 = k − m è un numero piccolo
relativamente sia a k
che ad m. Tenendo
fissa la posizione x,
al variare del tempo in questa posizione si vede passare l’onda
cos k+m
2 (x − vt) ∼ cos k(x − vt), modulata dal segnale
di bassa frequenza 2A cos k−m
2 (x − vt).
Se l’onda in questione è un’onda sonora, nella posizione
x si sente un suono di
frequenza circa uguale a kv∕2π,
ed ampiezza 2A cos[(k − m)(x − vt)∕2]
lentamente variabile nel tempo, con legge periodica di “piccola“ frequenza
(k − m)v∕(4π). Si
ricordi che la minima frequenza dei suoni udibili dall’orecchio umano è
16 Herz.
Se accade che
(k − m)v
4π > 16
l’orecchio sente comparire un “terzo suono”, diverso dai due suoni emessi dagli
strumenti, ed in generale sgradevole. Questo suono si chiama appunto terzo suono o
suono di Tartini Il caso estremo si ha quando le due onde hanno il medesimo
numero d’onde e la medesima velocità, ma si propagano in verso opposto,
v = −ν. In
tal caso si trova
|
2A cos kx cos kvt.
| (4.14) |
In questo caso niente si propaga: la somma di onde uguali
propagantesi in versi opposti genera una configurazione
A cos kx, stazionaria, “modulata”
dal segnale sovrapposto cos kvt.
Nonostante che in questo caso niente si propaghi, per conservare la memoria
dell’origine di questo fenomeno, si chiama ancora “onda” la funzione (4.14) e, per
sottolineare che “niente si propaga”, la chiamiamo onda stazionaria
Interferenza
Consideriamo ora due onde uguali, ossia con la medesima ampiezza, numero d’onde
e velocità di propagazione, ma sfasate l’una rispetto all’alta. Ossia consideriamo le
due onde
f(x − vt) = A cos k(x − vt),g(x − vt) = A cos k(x − vt + ϕ).
Se queste due onde si propagano nel medesimo mezzo, il segnale propagantesi nel
mezzo è
A cos k(x − vt) + cos k(x − vt + ϕ) = 2A cos kϕ
2 cos kx − vt + ϕ
2 .
Si ha quindi un segnale di ampiezza 2A cos kϕ∕2.
che può essere nulla. In pratica, la differenza di fase è dovuta alla differente
lunghezza del cammino percorso dalle due onde; e quindi in realtà
ϕ varia cambiando
posizione, ϕ = ϕ(x).
Se l’onda in questione è un’onda sonora, in un punto
x
fissato si sente un suono uguale a quello descritto da
f(x), ma
con una diversa intensità. L’intensità varia al variare della posizione d’ascolto e
in certe posizioni può annullarsi. Questo fenomeno si chiama interferenza delle due
onde.
4.7.3 Appendice: Funzioni omogenee
Una funzione f(r→), con
r→ ∈ ℝn, si chiama positivamente
omogenea di grado ν
(anche non intero) se
f(tr→) = |t|νf(r→).
Supponiamo che una funzione omogenea di grado
ν sia di
classe C1 per
r→≠0. Derivando rispetto
a t i due membri e
calcolando le derivate per t = 1,
si trova l’uguaglianza
|
∇f(r→) ⋅r→ = νf(r→)∀r→.
| (4.15) |
Questa relazione si chiama identità di Eulero e caratterizza le funzioni omogenee e di
classe C1 (per
r→≠0) di grado
ν. Infatti,
consideriamo il caso t > 0.
Derivando la funzione
t−νf(tr→)
si trova
|
d
dtt−νf(tr→) = −νt−ν−1f(tr→) + t−ν(∇f(tr→) ⋅r→)
= t−ν−1 −νf(tr→) + ∇f(tr→) ⋅ (tr→) .
|
Per ipotesi la (4.15) vale per ogni
r→; in particolare
vale nel punto tr→,
ossia vale
νf(t,r→) = ∇f(t,r→) ⋅ (tr→);
e quindi
d
dtt−νf(tr→) = 0.
Dunque,
t−νf(tr→) = c,ossiaf(tr→) = ctν
ove c è una opportuna
costante. Ponendo t = 1
si trova c = f(r→)
e quindi
f(tr→) = tνf(r→).
In modo analogo si procede per t < 0
e quindi si trova che la funzione è omogenea di grado
ν.
4.7.4 Appendice: La dimostrazione del teorema 132
Dim. Per semplicità di notazioni, proviamo l’asserto con
x0 = 0,
y0 = 0. fissiamo
i punti x
ed y e
consideriamo la funzione di una sola variabile
ϕ(t) = f(tx,ty).
Si noti che ϕ(1) = f(x,y)
mentre ϕ(0) = f(0, 0).
Scriviamo
ϕ(t) = {f(tx,ty) − f(tx, 0)} + {f(tx, 0) − f(0, 0)}.
Consideriamo la funzione della sola variabile
t
m(t) = f(tx, 0).
In quest’espressione, il numero x
si considera come un parametro il cui valore è fissato.
Applichiamo ad essa la seconda formula degli incrementi finiti: esiste
c ∈ (0, 1) tale
che
f(x, 0) − f(0, 0) = m(1) − m(0) = d
dtm(t)|t=c = xfx(cx, 0).
Si noti che si sono usate in questo calcolo solamente proprietà delle
funzioni di una variabile e che, per applicare la seconda formula
degli incrementi finiti, si è usata l’esistenza della derivata di
f(tx, 0) che, a sua volta, implica la
continuità di f(tx, 0). Il numero
c dipende dalla particolare
funzione m(t) usata e quindi,
in definitiva, dipende da x.
Dato che c ∈ (0, 1),
si ha |cx| < |x|.
Usando ciò, stimiamo
x fx(cx, 0) − fx(0, 0)
x2 + y2 ≤fx(cx, 0) − fx(0, 0) .
La condizione |cx| < |x|
e la continuità della derivata prima mostrano che il limite per
(x2 + y2)
tendente a zero è nullo. Dunque vale
|
f(x, 0) − f(0, 0) = xfx(0, 0) + o(x,y).
| (4.16) |
Consideriamo ora la funzione n(τ),
dipendente dai parametri x
ed y,
n(τ) = f(x,τy).
Applicando a questa la seconda formula degli incrementi finiti, si trova
d ∈ (0, 1) tale
che
f(x,τy) − f(x, 0) = n(1) − n(0) = d
dτn(τ)|τ=c̃ = yfy(x,dy).
Si noti che il numero d
dipende dalla particolare funzione con cui si lavora, e quindi dai parametri
x ed
y
che la identificano. E’ però un numero compreso tra
0 ed
1. La precedente uguaglianza
vale per ogni τ ∈ (0, 1), in particolare
essa vale se come valore di τ
si sceglie 1:
f(x,y) − f(x, 0) = yfy(x,dy) = yfy(0, 0) + y fy(x,dy) − fy(0, 0) .
L’ultima differenza verifica
y fy(x,dy) − fy(0, 0)
x2 + y2 ≤|fy(x,dy) − fy(0, 0)|
e quindi tende a zero per dist((x,y), (0, 0)) tendente
a zero, per la continuità di fy
e perchè 0 < d < 1.
Dunque si può scrivere
|
f(x,y) − f(x, 0) = yfy(0, 0) + o(x,y).
| (4.17) |
Sommando la (4.16) e la (4.17) si trova la formula cercata. _
Osservazione 157 Si noti che per la dimostrazione è suffciente sapere che
la funzione f(x,y)
è derivabile ed ha derivate continue in un intorno di (x0,y0). _
4.7.5 Appendice: la dimostrazione del teorema di Schwarz
La dimostrazione del teorema di Schwarz è importante anche perché fornisce un’ulteriore
rappresentazione delle derivate miste. Limitiamoci a provare il teorema assumendo
(x0,y0) = (0, 0). Mostriamo
che, se fx,y(x,y) ed
fy,x(x,y) sono continue
in un intorno di (0, 0)
allora si ha
|
fxy(0, 0) = lim (h,k)→(0,0)f(h,k) − f(h, 0) − f(0,k) + f(0, 0)
hk = fy,x(0, 0).
| (4.18) |
L’uguaglianza implica in particolare che le derivate miste sono uguali. Introduciamo
la funzione ϕ(x) = f(x,k) − f(x, 0).
Vale:
ϕ(h) − ϕ(0) = f(h,k) − f(h, 0) − f(0,k) + f(0, 0).
Dal Teorema di Lagrange si ha
ϕ(h) − ϕ(0) = hϕ′(c) = h[f
x(c,k) − fx(c, 0)].
Il numero c
dipende sia da h
che da k,
c = c(h,k) e
verifica
0 < c(h,k) < k.
Si usi ora la continuità della derivata
fx(x,y), l’esistenza in ogni
punto della derivata fxy(x,y)
e di nuovo il Teorema di Lagrange per scrivere
ϕ(h) − ϕ(0) = h[fx(c,k) − fx(c, 0)] = hk[fxy(c(h,k),d)].
Il punto d
dipende da k e
da c, quindi in
definitiva da h
e da k,
d = d(h,k), e
verifica
0 < d(h,k) < k.
Dunque, dal Teorema di confronto per i limiti,
lim (h,k)→(0,0)c(h,k) = 0, lim (h,k)→(0,0)d(h,k) = 0
cosìche, per la continuità della derivata seconda mista
lim (h,k)→(0,0)ϕ(h) − ϕ(0)
hk = lim (h,k)→(0,0)fxy(c(h,k),d(h,k)) = fxy(0, 0).
Ciò prova la prima uguaglianza in (4.18). Per provare la seconda uguaglianza si
introduca la funzione
ψ(y) = f(h,y) − f(0,y).
Si procede in modo analogo a quanto fatto per la funzione
ϕ(x) e si
trova:
- ψ(k) − ψ(0) = f(h,k) − f(0,k) − f(h, 0) + f(0, 0)
= f(h,k) − f(h, 0) − f(0,k) + f(0, 0) = ϕ(h) − ϕ(0);
- lim (h,k)→(0,0)ψ(k)−ψ(0)
hk = fyx(0, 0) = lim (h,k)→(0,0)ϕ(h)−ϕ(0)
hk = fx,y(0, 0)
e quindi fxy(0, 0) = fyx(0, 0). _
Osservazione 158 Si noto che:
- per la dimostrazione del teorema di Schwartz basta che la funzione sia di
classe C1(V ),
con V
intorno di (x0,y0);
che esistono le derivate seconde miste in ogni punto di V
e che queste sono continue in (x0,y0).
Le derivate fxx(x,y),
fyy(x,y)
non intervengono.
- Supponiamo che la funzione dipenda da tre o più variabili e che x
ed y
denotino due delle variabili. Nel fare le derivate rispetto ad x
ed y,
tutte le altre variabili vengono tenute costanti; e quindi il teorema di
Schwarz vale per funzioni di classe C1,
qualunque sia il numero di variabili da cui la funzione dipende; e per tutte
le coppie (x,y)
di variabili tali che le rispettive derivate seconde miste siano continue.
Capitolo 5
Funzioni implicite ed estremi vincolati
I termini “curva” o “superficie” hanno vari significati, tra loro interdipendenti. E’
comodo conoscere da subito il significato di curva o superficie parametrica: diremo
che una curva è definita parametricamente quando è espressa mediante
un’equazione
x = x(t),y = y(t),t ∈ (a,b)
(se la curva è in ℝ3 c’è anche
una terza componente, z = z(t)).
Una superficie è definita parametricamente quando è definita mediante una trasformazione
da una regione Ω
di ℝ2 in
ℝ3,
x = x(u,v),y = y(u,v),z = z(u,v),(u,v) ∈ Ω.
Osserviamo che ogni grafico di funzione è una curva, o una
superficie, definita parametricamente. Infatti, considerando la funzione
f(x) della
variable x ∈ (a,b),
il suo grafico è identificato dalle equazioni
x = t,y = f(t)t ∈ (a,b).
In modo analogo, se la funzione dipende da due variabili
x ed
y, il
suo grafico è la superficie parametrica
x = u,y = v,z = f(u,v).
Se accade che una curva è grafico di una funzione
y = y(x) oppure
x = x(y), diciamo
che γ
è una curva cartesiana In modo analogo si definiscono le superfici
cartesiane come quelle superfici che sono grafici di funzioni di due variabili.
Chiameremo “curva” anche l’insieme immagine della parametrizzazione. Al
Cap. 6 saremo più precisi su questo punto. D’altra parte, si sa che la
geometria analitica definisce curve e superfici mediante equazioni: l’equazione
x2 + y2 = R2 definisce una
circonferenza di raggio R
(se R > 0;
altrimenti definisce un solo punto). In questo paragrafo vogliamo dare condizioni
perché un’equazione definisca una “curva” o una “superficie” in un senso che
spegheremo, e vogliamo studiare problemi di massimo e di minimo “vincolati“ a tali
curve o superfici.
5.1 Insiemi di livello
Sia F(r→) una funzione
definita su una regione Ω ⊆ ℝn
ed a valori in ℝ e si voglia
studiare l’equazione F(r→) = c.
Gli insiemi
ℱc = {r→|F(r→) = c}
si chiamano insiemi di livello della funzione
F(r→). Più precisamente,
l’insieme ℱc si chiama
l’insieme di livello c.
Notiamo esplicitamente che l’insieme di livello è un sottinsieme
del dominio della funzione e non del suo grafico. Per esempio se
r→ = (x,y)
l’insieme di livello si ottiene concettualmente con i tre passi seguenti:
- si costruisce il grafico della funzione, che è in ℝ3;
- si taglia il grafico col piano z = c;
- si proietta ortogonalmente la sezione ottenuta sul piano (x,y),
ottenendo l’insieme ℱc.
L’insieme ℱc
può avere la natura più varia, come mostrano gli esempi seguenti, nei quali
Ω = ℝ2 e
c = 0:
Esaminiamo più in dettaglio l’esempio 7. Come si è visto, si tratta di una curva parametrica. Se
(x0,y0) è una soluzione,
ossia un punto di ℱ0,
allora anche (x0,−y0) è
soluzione; e quindi l’insieme delle soluzioni non è un grafico di funzione (univoca). E’ però
vero che se |y0|≠0,
tagliando l’insieme delle soluzioni con una striscia
y0 − 𝜖 < y < y0 + 𝜖,
con 𝜖
abbastanza piccolo, si trova il grafico di una funzione
y = y(x).
Si veda la figura (5.1), a sinistra.
In questo caso particolare è facile determinare esplictamente la funzione,
perché
y(x) = 1 − x2sey0 > 0,y(x) = −1 − x2sey0 < 0.
Se invece y0 = 0,
l’insieme
{(x,y)|y0 − 𝜖 < y < y0 + 𝜖}∩{(x,y)|x2 + y2 = 1}
non è grafico di una funzione y = y(x).
E’ però grafico di una funzione x = x(y).
Per contrasto, vediamo l’esempio seguente:
- Esempio 8 E’ ancora c = 0
mentre la funzione F(x,y)
è
x2 − y2 = 0.
Quest’equazione è soddisfatta dai punti di ambedue le bisettrici e
l’intersezione delle bisettrici con un intorno di O
non è un grafico, né di una funzione y = y(x)
né di una funzione x = x(y),
si veda la figura (5.1), a destra.
Si pone quindi questo problema: supponiamo che l’insieme
ℱc sia non vuoto, e se ne
conosca un suo punto r→0.
Vogliamo dare condizioni sotto le quali esiste un intorno
W di
r→0 tale
che W ∩ℱc
sia una curva o una superficie cartesiana. Limitandoci al caso
n = 2 oppure
n = 3. Se
n = 2,
vogliamo capire se l’equazione
F(x,y) = c
si può “risolvere” rispetto per esempio ad
y, intendendo
x
come “parametro libero” ottenendo come grafico della funzione
(x,y(x)) l’insieme
W ∩ℱc; Se
n = 3,
vogliamo capire se l’equazione
F(x,y,z) = c
si può “risolvere” rispetto per esempio a
z, intendendo
(x,y)
come “parametro libero” ottenendo come grafico della funzione
(z,z(x,y)) l’insieme
W ∩ℱc. Quando
ciò accade, si dice che l’equazione considerata definisce implicitamente la funzione,
rispettivamente y = y(x)
oppure z = z(x,y).
Ciò si vedrà nel prossimo paragrafo, nel quale illustreremo anche il caso di un
sistema di due equazioni in tre variabili:
F1(x,y,z) = c1,F2(x,y,z) = c2.
Ci si chiede se, in un opportuno intorno di un punto
(x0,y0,z0), è
possibile risolvere questo sistema rispetto a due “incognite” per esempio
y e
z, intendendo
x come
“parametro libero”. Se ciò può farsi diremo che si è definita implicitamente una
funzione, che si interpreta come curva ottenuta come intersezione di due
superfici.
5.2 Il teorema della funzione implicita
Ricordiamo il problema: si ha un’equazione (o un sistema di equazioni)
di cui si conosce una soluzione: si vuol sapere se l’insieme delle soluzioni
è, localmente in un intorno di tale punto, una curva o una superficie
cartesiana. Considereremo con qualche dettaglio il caso di equazioni
F(x,y) = c
mentre ci limiteremo ad enunciare i risultati in due casi più generali.
5.2.1 Curve piane definite implicitamente
Ricordiamo il problema che si vuole studiare: Consideriamo l’equazione Sia
(x0,y0) una
soluzione dell’equazione
Vogliamo dare condizioni suffcienti per l’esistenza di un intorno
W di
(x0,y0) e di una
funzione y = y(x)
oppure x = x(y)
tali che
{(x,y) ∈ W|f(x,y) = c} = {(x,y) ∈ W|y = y(x)}
oppure
{(x,y) ∈ W|f(x,y) = c} = {(x,y) ∈ W|x = x(y)}.
La condizione che stiamo cercando è data dal teorema seguente:
Teorema 159 (della funzione implicita) Teorema della funzione implicita
Sia F(x,y)
una funzione di classe C1(Ω)
e sia (x0,y0) ∈ Ω.
Se
∇F(x0,y0)≠0 →
esiste un intorno
W
di
(x0,y0)
tale che
W ∩{(x,y)|F(x,y) = F(x0,y0)}
è grafico di una funzione y = y(x),
oppure x = x(y).
Più precisamente, se Fy(x0,y0)≠0
allora l’equazione (5.1) definisce implicitamente una funzione y = y(x)
di classe C1,
e vale
y′(x
0) = − Fx(x0,y0)
Ffy(x0,y0);
Se Fx(x0,y0)≠0
allora l’equazione (5.1) definisce implicitamente una funzione x = x(y)
di classe C1,
e vale
x′(y
0) = −Fy(x0,y0)
Fx(x0,y0).
Se ambedue le componenti di ∇F(x0,y0)
sono non nulle, allora l’equazione F(x,y) = f(x0,y0)
definisce implicitamente sia una funzione y = y(x)
che una funzione x = x(y).
Presentiamo (una parte della) dimostrazione di questo teorema, fissando l’attenzione sul
caso Fy(x0,y0)≠0. Il
punto (x0,y0)
è uno dei punti nel quale vale l’uguaglianza (5.1), ossia si ha
|
F(x,y) = c = F(x0,y0).
| (5.2) |
In tal caso, proviamo Si ha:
Teorema 160 Valga F(x0,y0) = c.
Sia F(x,y) di
classe C1 e sia
Fy(x0,y0)≠0. Sotto queste condizioni,
esistono un intorno U
di x0 ed un
intorno V di
y0 ed esiste un’unica
funzione y = y(x)
definita in U ed
a valori in V
che ha per grafico l’insieme (5.2) ossia tale che
- y(x0) = y0,
- F(x,y(x)) = c
per ogni x ∈ U,
- y(x) ∈ V .
Questa funzione è di classe C1
e inoltre
|
y′(x
0) = −Fx(x0,y0)
Fy(x0,y0).
| (5.3) |
Dim. Per seguire questa dimostrazione, si guardi la figura 5.2. In questa
figura,
x0 = y0 = 3
e il punto
(x0,y0)
è indicato con un asterisco.
Per il teorema della permanenza del segno, vale
Fy(x,y) > 0 in un
intorno W
di (x0,y0). Siano
Ũ0 un intorno
di x0 e
Ṽ0 un intorno
di y0 tali
che se x ∈Ũ0,
y ∈Ṽ0 allora
(x,y) ∈ W. Limitiamoci a
considerare le coppie (x,y)
con x ∈Ũ0,
y ∈Ṽ0. Siano
y1,
y2 elementi
di Ṽ0
tali che
y1 < y0 < y2.
Consideriamo la funzione ϕ(y) = F(x0,y).
Questa funzione è continua e strettamente crescente e
ϕ(y0) = c. Dunque,
ϕ(y1) < c,
ϕ(y2) > c.
Il Teorema della permanenza del segno mostra l’esistenza di un intorno
U ⊆Ũ0 di
x0 tale
che
F(x,y1) < c,F(x,y2) > c∀x ∈ U;
e, per ogni fissato x ∈ U, la funzione
y → F(x,y) è strettamente crescente.
Dunque, per x fissato,
esiste un unico numero y = y(x) ∈Ṽ
tale che
F(x,y(x)) = c.
Ciò prova l’esistenza della funzione y(x).
Omettiamo la dimostrazione della regolarità. Accettando il fatto non provato che
y(x) è
derivabile, si derivino i due membri dell’uguaglianza
F(x,y(x)) = 0.
Si trova, per il Teorema 135,
0 = Fx(x,y(x)) + Fy(x,y(x))y′(x)
e quindi
y′(x) = −Fx(x,y(x))
Fy(x,y(x)).
Calcolando per x = x0 si trova
la (5.3) _ La funzione y = y(x)
cosìcostruita si dece definita implicitamente dall’equazione (5.1).
5.2.2 Superfici definite implicitamente
Consideriamo ora l’equazione
|
F(x,y,z) = c = F(x0,y0,z0).
| (5.4) |
Vogliamo dare condizioni sotto le quali sia possibile considerare due delle tre
variabili come “parametri liberi” e risolvere rispetto alla terza, ottenendo quindi per
esempio una funzione implicita
z = z(x,y)
che interpretiamo come equazione cartesiana di una superficie. Limitiamoci ad
enunciare il teorema che dà una condizione solamente suffciente per l’esistenza
della funzione implicita.
Teorema 161 Sia F(r→,z)
una funzione a valori reali della variabile (r→,z) ∈ ℝn
(z
indica l’ultima componente del vettore (r→,z)
e pertanto è un numero reale). Supponiamo che la funzione sia di classe
C1
e che valga
F(r→0,z0) = c,Fy(r→0,z0)≠0.
Esiste un intorno
W
di
(r→0,z0)
ed esiste un’unica funzione
z = z(r→)
tale che
{(r→,z) ∈ W|F(r→,z) = c = F(r→0,z0)} = {(r→,z) ∈ W|z = z(r→)}.
La funzione z(r→)
è di classe C1
ed il suo gradiente è (indicando con x1,…,xn−1
le componenti di r→)
− 1
Fz(r→0,z0) Fx1(r→0,z0)Fx2(r→0,z0)…Fxn−1(r→0,z0) ′.
Nel caso particolare r→ = (x,y)
la funzione che si trova è
z = z(x,y),
ossia la rappresentazione parametrica di una superficie cartesiana.
Osservazione 162 Il teorema precedente si può applicare ad una qualsiasi
delle variabili, purché la derivata parziale relativa sia non nulla; per esempio,
si potrà applicare alla prima invece che all’ultima componente. _
5.2.3 Curve intersezione di due superfici
Studiamo ora un sistema di due equazioni in tre incognite. Consideriamo prima di
tutto un esempio:
Esempio 163 Studiamo il problema
x2 + y = 1,y − x + z = 0.
Questo sistema può scriversi come
z = x2 + x − 1,y = 1 − x2,
ossia il sistema ha infinite soluzioni, una per ogni valore di x.
Diremo che questo sistema definisce implicitamente le due funzioni z(x) = x2 + x − 1
e y(x) = 1 − x2
o meglio diremo che definisce una funzione della variabile reale x,
a valori in ℝ2. _
Consideriamo in generale il sistema delle due equazioni in tre incognite
|
f(x,y,z) = c,g(x,y,z) = d.
| (5.5) |
Supponiamo che (x0,y0,z0) risolva
questo sistema e, fissato x0,
consideriamo la funzione F→(y,z)
da ℝ2 in
ℝ2
F→(y,z) = F(x0,y,z)
G(x0,y,z) .
Lo jacobiano di questa trasformazione è
j(x0,y,z) = det Fy(x0,y,z)Fz(x0,y,z)
Fy(x0,y,z)Fz(x0,y,z) .
Vale:
Teorema 164 Siano
F(x,y,z)
e
F(x,y,z)
funzioni di classe
C1
e sia
j(x0,y0,z0)≠0.
Esiste un intorno W
di (x0,y0,z0) ed una unica
funzione di classe C1
da ℝ
in ℝ2,
tale che
{(x,y,z) ∈ W, soluzioni di (5.5)} = {(x,y,z)|y = ϕ(x),z = ψ(x)}.
La derivata della funzione x →ϕ(x)ψ(x) ′
è
d
dt ϕ(x0)
ψ(x0) = −Fy(x0,y0,z0)Fz(x0,y0,z0)
Gy(x0,y0,z0)Gz(x0,y0,z0) −1 Fx(x0,y0,z0)
Gx(x0,y0,z0) .
Omettiamo la dimostrazione. Naturalmente diremo che la funzione (5.6) è definita
implicitamente dal sistema di equazioni (5.5).
5.3 Il teorema della funzione inversa ed i cambiamenti di variabili
Il teorema della funzione inversa si può vedere come ulteriore caso del
teorema della funzione implicita, nel caso in cui l’equazione da risolvere
sia
F→(r→) = x→,r→ ∈ ℝn,x→ ∈ ℝn
ma conviene vederlo come studio dei cambiamenti di
variabile Cominciamo ad illustrarlo nel caso più semplice
n = 1. Abbiamo quindi una
funzione F(x) di una sola
variabile x definita su
un intervallo (a,b) ed ivi di
classe C1. Se la sua derivata
non si annulla, si ha F′(x) > 0
oppure F′(x) < 0 in ogni
punto di (a,b) e quindi
F(x) è strettamente
monotona su (a,b).
Dunque è invertibile. E’ naturale investigare se l’osservazione precedente
possa estendersi al caso di funzioni di più variabili. Lo studio di questo
problema conduce al “teorema della funzione inversa”, di cui ora illustriamo
l’interesse. Abbiamo visto che talvolta conviene rappresentare i punti di
ℝ3
mediante coordinate sferiche oppure, a seconda delle applicazioni, cilindriche.
In altri casi si usano coordinate ellittiche che, sul piano, sono date dalle
trasformazioni
x = ra cos 𝜃,y = rb sin 𝜃,r > 0,𝜃 ∈ [0, 2π).
In generale si ha questa situazione: si hanno due regioni
Ω ed
Ω′ di
ℝn
(conviene considerarle in due “copie diverse” di
ℝn) e una trasformazione
invertibile x→ = F→(r→) da
Ω′ con immagine
uguale ad Ω. In questo
caso i punti di Ω
si possono rappresentare, invece che con le loro coordinate cartesiane, con quelle del
punto r→
di Ω′ che
univocamente gli corrisponde. Per esempio lavorando con coordinate polari nel
piano,
r→ = (r,𝜃) ∈ (0, +∞)×[−π,π),x→ = (x,y) : x = r cos 𝜃 y = r sin 𝜃.
Questa è una trasformazione invertibile dalla striscia
Ω = (0, +∞) × (−π,π) alla regione
Ω che è il
piano ℝ2 privato
del semiasse {(x,y),x ≤ 0}.
Per molte applicazione è necessario che la trasformazione sia oltre che invertibile
anche differenziabile e con inversa essa stessa differenziabile. In pratica non è
diffcile riconoscere che la trasformazione con cui si lavora è differenziabile,
e spesso anche riconoscere che è invertibile; è più diffcile calcolare
esplicitamente l’inversa e verificare che essa è differenziabile. Fortunatamente
il teorema seguente dà una condizione suffciente per l’invertibilità (si
noti: solamente locale) e per la differenziabilità della funzione inversa.
Teorema 165 (teorema della funzione inversa) Sia x→ = F→(r→)
una funzione definita su un aperto Ω′ ⊆ ℝn
ed a valori in ℝn,
di classe C1(Ω′).
Sia r→0 ∈ Ω′
un punto in cui il determinante jacobiano è diverso da zero:
det JF→(r→0)≠0.
Sotto tali condizioni esistono un aperto
A contenente
r→0 ed un
aperto B
contenente x→0 = F→(r→0)
con queste proprietà:
Si noti che, accettando la differenziabilità della funzione inversa, la formula per
JG→(x→0)
discende dalla formula di derivazione a catena. Infatti, sia
G→(x→) la funzione inversa
di F→(r→) e supponiamo di
sapere che la funzione G→(x→)
è differenziabile. Per la definizione di funzione inversa,
G→(F→(r→)) = r→.
La matrice jacobiana della trasformazione
r→ →r→ è
I, la
matrice identità. Dunque, dalla formula di derivazione a catena,
I = JG→(x→0)JF→(r→0),x0 = F→(r→0)
ossia
JG→(x→0) = JF→(r→0) −1.
E’ importante notare che il teorema della funzione inversa afferma:
- l’invertibilità locale;
- la regolarità dell’inversa.
Invece, l’invertibilità su tutta Ω
generalmente non vale, come prova il caso delle coordinate polari nel piano. Per esse, lo jacobiano
è uguale ad r e
quindi non nullo per r > 0
e qualunque 𝜃;
ma se vogliamo una trasformazione biunivoca dobbiamo imporre a
𝜃
di appartenere ad un intervallo di lunghezza non maggiore di
2π. Il
teorema della funzione inversa ha numerose dimostrazioni, tutte interessanti. In
appendice mostriamo una dimostrazione nel caso di una trasformazione da
ℝ2 in
sé, basata sul teorema della funzione implicita.
In questo capitolo assumeremo che
F
sia di classe C1
e che gli zeri di ∇F
siano isolati. Ricordiamo che i punti nei quali
∇F(x0,y0) = 0
si chiamano punti critici della funzione
F.
5.4 Ulteriori esempi
Ricordiamo che il Teorema della funzione implicita dà una condizione suffciente
perchè un insieme di livello sia localmente grafico di una funzione: se
F(x,y) è di
classe C1, se
esiste (x0,y0) tale
che F(x0,y0) = c e se
Fy(x0,y0)≠0, allora esiste
un intorno W
di (x0,y0) la
cui intersezione con l’insieme di livello è grafico di una (unica) funzione
y = y(x).
Analogo risultato vale se Fx(x0,y0)≠0. In
questo caso la funzione è x = x(y).
Si ricordi che questa condizione è solamente suffciente, e non necessaria, come
prova l’esempio seguente:
Esempio 166 La funzione F(x,y) = (x − y)2
definisce implicitamente la funzione x = y.
Ma in (0, 0)
le sue derivate sono identicamente nulle. _
fissiamo un punto (x0,y0)
tale che ∇F(x0,y0)≠0.
Chiamiamo curva di livello o curva definita implicitamente l’insieme
γ = {(x,y)|F(x,y) = F(x0,y0)}.
Si noti che potrebbero esistere punti (x,y) ∈ γ
nei quali il gradiente si annulla. Noi abbiamo richiesto solamente che
∇F(x0,y0)≠0.
Ovviamente, ogni grafico di funzione è una curva definita implicitamente
dall’equazione
F(x,y) = y − f(x) = 0.
Si ricordi che avevamo già notato che gni grafico di funzione è anche curva definita
parametricamente. Se ∇F(x0,y0)≠0,
esiste un intorno W
di (x0,y0) tale
che W ∩ γ
è grafico di una funzione. Per esempio di una funzione
y = y(x). E’ quindi possibile
definire la tangente in (x0,y(x0)) = (x0,y0)
a tale grafico. Per definizione, la chiamiamo tangente alla curva
γ nel
punto (x0,y0).
La retta tangente è
|
y = y(x0) + y′(x
0)(x − x0)
= y(x0) −Fx(x0,y0)
Fy(x0,y0)(x − x0).
|
Essendo F(x,y(x))
identicamente nulla, la sua derivata è zero. La derivata per
x = x0
è
∇F(x0,y0)⋅1y′(x
0) ,
ossia, ∇F(x0,y0) è
ortogonale alla tangente. Per definizione, diremo che il gradiente è ortogonale alla
curva. Si ha quindi: Dunque:
Teorema 167 Sia γ
è una curva di livello di una funzione F(x,y)
di classe C1.
Il gradiente di F(x,y)
in ciascuno dei punti di γ
che non sono punti cretici di F,
è ortogonale alla curva stessa.
Per concludere, mostriamo che niente può dirsi nei punti nei quali le condizioni del
teorema della funzione implicita non valgono. Abbiamo già visto (esempio 166)
una funzione che non soddisfa alle condizioni del teorema della funzione
implicita, ma che definisce implicitamente una funzione regolare. D’altra parte:
Esempio 168 Consideriamo l’equazione
F(x,y) = y2 − x2 = 0.
Le due derivate parziali si annullano in (0, 0).
L’equazione si risolve facilmente, trovando le soluzioni
y = x,y = −x.
La figura 5.3 a sinistra mostra che l’insieme di livello non è una curva
cartesiana in nessun intorno dell’origine. A destra mostra la superficie (un
paraboloide a sella) di cui si considera l’insieme di livello. Consideriamo ora
l’equazione
F(x,y) = y3 − x2 = 0
Ancora si annullano le due derivate parziali di F(x,y)
in (0, 0).
L’equazione definisce però un’unica funzione,
y = x23.
Questa funzione non è derivabile in y = 0.
Il suo grafico è nella figura 5.4, a destra mentre a sinistra è rappresentata
la funzione di cui si calcola la curva di livello. _
Infine, consideriamo l’esempio seguente
Esempio 169 La funzione che si considera è
|
f(x,y) = {[(x − 2)2 + y2][(x + 2)2 + y2]}1∕5,
| (5.8) |
il cui grafico è riportato nella figura 5.5, a sinistra. A destra si riportano
alcune delle sue curve di livello, corrispondenti a varie quote.
Si noti che, per quote basse, la “curva di livello” si spezza in due curve e per
quota uguale a 0
si riduce a due punti (i due punti di minimo della funzione). La funzione ha un
punto di sella di coordinate (0,0, 1). La curva di livello 1
ha un “punto doppio” in (0, 0). _
Il teorema della funzione implicita asserisce che se
∇f(x0,y0)≠0 (ed
f(x,y) è di classe
C1) allora in un
intorno di (x0,y0)
la curva di livello
f(x,y) = f(x0,y0)
è grafico di una funzione y = y(x)
oppure x = x(y).
Si sa già che curva di livello può essere un grafico anche se
∇f(x0,y0) = 0.
L’esempio seguente ribadisce questo fatto.
Esempio 170 La funzione è
f(x,y) = y3 − x2y2 + x2y − x4
e il punto (x0,y0)
è (0, 0).
E’: ∇f(0, 0) = 0.
Ciò nonostante, la curva di livello f(x,y) = f(0, 0) = 0
è la parabola y = x2
perché
f(x,y) = (y − x2)(y2 + x2).
La figura 5.6 mostra a sinistra il grafico di
z = f(x,y)
e la sua intersezione col piano z = 0;
a destra varie curve di livello della funzione.
5.4.1 Superfici assegnate in modo implicito e curve intersezione di due
superfici
Cosìcome le curve, anche le superfici possono assegnarsi in modo implicito. Sia
F(r→) = F(x,y,z) una funzione di tre
variabili, di classe C1,
e si voglia risolvere l’equazione
F(x,y,z) = c.
Sia r→0 = (x0,y0,z0)
un punto che verifica l’equazione. Dal Teorema delle funzioni implicite si sa che
se
Fz(r→0)≠0
allora esiste un intorno W
di r→0 ed esiste
una funzione z = ϕ(x,y)
per cui
{(x,y,z) ∈ W|F(x,y,z) = c} = {(x,y,z) ∈ W|z = ϕ(x,y)}.
Ossia, localmente l’insieme delle soluzioni è il grafico della funzione
z = ϕ(x,y). Discorso
analogo vale se una delle altre due derivate parziali è non nulla. Di conseguenza, se
∇F(x,y,z) non si annulla, ogni
insieme di livello di F(r→)
è “fatto di tanti pezzi di grafici, e quindi di superfici”. Usa considerare anche un
tale insieme una superficie definita però in modo implicito. Si abbiano ora due
superfici definite in modo implicito da
f(x,y,z) = c,g(x,y,z) = d.
I punti (x,y,z)
che appartengono all’intersezione dei due sostegni risolvono il sistema
|
f(x,y,z) = c,g(x,y,z) = d.
| (5.9) |
Sia (x0,y0,z0)
una soluzione di questo sistema. Se lo jacobiano
det fy(x0,y0,z0)gy(x0,y0,z0)
fz(x0,y0,z0)gz(x0,y0,z0)
non è nullo, si sa (dal Teorema 164) che l’insieme delle
soluzioni di (5.9) che appartiene ad un opportuno intorno
W di
(x0,y0,z0) ha
forma
y = ϕ(x),z = ψ(x)
e quindi è una curva cartesiana di ℝ3;
ossia, localmente l’insieme delle soluzioni di (5.9) è una curva. Chiameremo ancora
curva l’insieme di tali soluzioni e, più precisamente, diremo che si tratta di una curva
ottenuta come intersezione di due superfici. La figura 5.7 illustra l’intersezione dei due
cilindri z = x2 e
z = y2.
5.5 Estremi vincolati
Diremo che un punto r→0,
rispettivamente o di γ
o di Σ,
è un massimo relativo, oppure un minimo relativo, di
g(r→) vincolato
a γ o a
Σ
quando è un massimo o un minimo della restrizione di
g(r→) alla curva
γ o, rispettivamente,
alla superficie Σ.
In questo capitolo vogliamo dare condizioni necessarie per gli estremi vincolati, che
estendano la condizione “derivata prima nulla nei punti estremi”.
Osservazione 171 Daremo condizioni solamente necessarieche devono venir
soddisfatte da un punto r→0
di massimo o di minimo vincolato ad una curva γ
o ad una superficie Σ,
definite implicitamente come curve, rispettivamente superficie, di livello di una
funzione di classe C1.
Quindi interessa solamente considerare il comportamento di F
e di g
in un intorno di r→0.
Dunque, non sarà necessario assumere che il gradiente di F
sia ovunque diverso da zero. Basterà assumere che sia ∇F(r→0)≠0.
Per continuità, il gradiente ∇F(r→)
sarà diverso da zero in un intorno di r→0. _
Esamineremo con qualche dettaglio il caso degli estremi vincolati ad una curva piana e,
per sommi capi, il caso degli estremi vincolati ad una superficie ed ad una curva
dello spazio.
5.5.1 Estremi vincolati ad una curva piana
Considerando ancora il caso di funzioni di due variabili, vogliamo studiare gli estremi di una funzione
g(x,y) vincolati ad una curva
γ; ossia, considerando i punti
di minimo, vogliamo
studiare quei punti (x0,y0) del
sostegno di γ con questa
proprietà: esiste un intorno I
di (x0,y0) tale che se
(x,y) ∈ I appartiene anche
al sostegno di γ
allora si ha
g(x0,y0) ≤ g(x,y).
Ovviamente, un caso è banale: se la curva
γ è
descritta parametricamente,
x = x(t),y = y(t)t ∈ (a,b)
il problema si riduce a studiare i punti di minimo relativo della funzione di una sola
variabile t → g(x(t),y(t)).
Il caso interessante è il caso in cui la curva è descritta in modo implicito. Il
problema di caratterizzare i punti di minimo ha carattere locale e, come si
è detto, nell’intorno di un punto nel quale il gradiente non si annulla,
ogni curva di livello può scriversi in forma parametrica. Però, in pratica,
trovarne l’espressione parametrica è tutt’altro che facile. Vogliamo quindi
dare una condizione necessaria soddisfatta dai punti di minimo, senza dover
esplicitare la curva di livello. Ricapitolando, è data una una funzione
F(x,y) di classe
C1 e un
punto (x0,y0).
Assumiamo
∇F(x0,y0)≠0.
E’ data una funzione g(x,y)
di classe C1 e supponiamo
che (x0,y0) sia punto di
minimo della g(x,y)
vincolato alla curva di livello
F(x,y) = F(x0,y0).
Una condizione necessaria che deve essere soddisfatta è data dal teorema
seguente.
Teorema 172 Siano
F(x,y)
e
g(x,y)
funzioni di classe
C1
su una regione
Ω
e sia
(x0,y0) ∈ Ω
un punto tale che
∇F(x0,y0)≠0.
Sia
γ
la curva di livello
F(x,y) = F(x0,y0).
Sia (x0,y0)
un punto di massimo o di minimo di g(x,y),
vincolato alla curva γ.
In tal caso esiste un numero λ
tale che
∇g(x0,y0) = λ∇F(x0,y0).
Il numero λ si
chiama moltiplicatore di Lagrange e quando si usa il teorema precedente per la
ricerca degli estremi vincolati si diche che si usa il metodo dei moltiplicatori di
Lagrange. Posponiamo la dimostrazione formale del teorema e presentiamone prima
di tutto una giustificazione di tipo geometrico.
Considerazioni geometriche che giustificano il metodo
dei moltiplicatori di Lagrange. fissiamo l’attenzione sul punto
(x0,y0) di
γ e consideriamo la
curva di livello σ
di g(x,y),
σ : g(x,y) = g(x0,y0).
Il punto (x0,y0) appartiene
sia a γ che a
σ. Supponiamo che
la γ passi da una
parte all’altra di σ.
In questo caso la γ
passa da una parte del piano in cui vale
g(x,y) < g(x0,y0)
ad una parte del piano in cui vale
g(x,y) > g(x0,y0)
e quindi il punto (x0,y0)
non è né di massimo né di minimo. Dunque, nei punti di massimo e di minimo vincolati, le due
curve di livello γ
e σ si
toccano senza attraversarsi. La fig. 5.8 illustra questo caso.
Usando gli sviluppi di Taylor si prova che le due curve
γ e
σ si attraversano nel
loro punto comune (x0,y0)
se le tangenti in tale punto si attraversano. Dunque nei punti di massimo e di minimo
vincolato le due curve devono avere la medesima retta tangente e quindi la medesima
retta normale. Questo caso è illustrato dalla figura 5.9 a sinistra mentre la
figura 5.9 a destra mostra che le due curve di livello possono attraversarsi anche nel
caso in cui le tangenti coincidono.
Sappiamo che la normale ad una curva di livello è nella direzione del gradiente
della funzione e quindi nei punti di massimo oppure di minimo vincolato,
∇F(x0,y0) e
∇g(x0,y0) sono vettori colineari:
esiste un numero λ
tale che ∇g(x0,y0) = λ∇F(x0,y0).
Dunque, studiando il sistema della tre equazioni
|
F(x,y) = 0
λFx(x,y) = gx(x,y)
λFy(x,y) = gy(x,y)
| (5.10) |
nelle tre incognite λ,
x ed
y, si
determinano dei punti tra i quali necessariamente si trovano gli estremi vincolati di
g(x,y).
Osservazione 173 Gli argomenti di tipo geometrico che abbiamo usato non
sono rigorosi e inoltre fanno intervenire la curva di livello σ.
Dunque implicitamente richiedono di lavorare in punti nei quali il gradiente
della funzione g(x,y)
non si annulla. Il teorema vale però anche se ∇g(x0,y0) = 0.
Infatti, la dimostrazione analitica presentata più avanti non fa uso di condizioni
sul gradiente di g(x,y).
I punti nei quali si annulla il gradiente di g(x,y)
si trovano dalle (5.10) scegliendo λ = 0. _
Alcuni esempi
Esempio 174 Si voglia calcolare il punto su una curva piana, più vicino
all’origine; ossia si voglia minimizzare sulla curva la funzione
g(x,y) = x2 + y2.
Consideriamo il caso delle quattro curve seguenti:
- la curva è implicitamente definita da
y2 − x + 1 = 0
ed è rappresentata in figura 5.10.
E’ facile vedere geometricamente che il punto del sostegno più vicino all’origine è il
punto (1, 0)
e questo è l’unico punto per cui esiste un
λ
tale che
y2 − x + 1 = 0
− 1 + 2λx = 0
y + λy = 0.
Il valore di λ
è 1∕2.
- Se F(x,y) = (y2 − x + 1)2
si ha il medesimo problema; ma ora il metodo dei moltiplicatori
di Lagrange non è applicabile perchè le derivate parziali di
F(x,y)
si annullano contemporaneamente. Tentando ugualmente di scrivere il
sistema (5.10) si trova
(y2 − x + 1)2 = 0
− (y2 − x + 1) + λx = 0
2(y2 − x + 1) + λ = 0.
Questo sistema non dà informazioni perché scegliendo
λ = 0 si vede
che ogni (x,y)
per cui y2 − x + 1 = 0
risolve le tre equazioni.
- Sia invece F(x,y) = x2 + y2 − 1.
Ovviamente, ogni punto della circonferenza minimizza la distanza. Però le due derivate
parziali di F(x,y) si
annullano in (0, 0).
Dato che (0, 0)
non appartiene alla curva, il metodo dei moltiplicatori di Lagrange può
usarsi. Il sistema (5.10) è ora
x2 + y2 − 1 = 0
2x + 2λx = 0
2y + 2λy = 0.
Ogni valore (x,y) per
cui x2 + y2 = 1 risolve questo
sistema (con λ = −1).
- Sia F(x,y) = 2x2 + y2 − 1.
Ancora, ambedue le derivate parziali di
F(x,y) si annullano
in (0, 0),
che però non appartiene alla curva. Dunque, il metodo dei moltiplicatori di
Lagrange può usarsi. Il sistema (5.10) diviene:
2x2 + y2 − 1 = 0
2x + λx = 0
y + λy = 0.
Le soluzioni sono ora
x = 0y = ±1 con λ = −1
y = 0x = ±1∕2con λ = −2.
Dato che f(x,y) è l’ellisse
in figura 5.8, i punti (±2, 0)
sono di minimo mentre (0,±1)
sono di massimo. Il metodo dei moltiplicatori di Lagrange, essendo solo basato
sullo studio delle derivata prima, non permette di distinguere un caso
dall’altro. _
Infine, applichiamo il metodo dei moltiplicatori di Lagrange per il calcolo dei punti
estremi di una funzione di una sola variabile.
Esempio 175 Sia g0(x)
una funzione derivabile della sola variable x ∈ ℝ.
Introduciamo la funzione g(x,y)
di due variabili, costante rispetto ad y,
data da
g(x,y) = g0(x).
Calcolare i punti estremi di
g0(x)
è come calcolare i punti estremi della funzione
g(x,y)
vincolati alla curva
F(x,y) = 0ove F(x,y) = y.
Si noti che la funzione
F(x,y)
è di classe
C1
ed ha gradiente non nullo:
∇F(x,y) = 0 1 .
Quindi i punti estremi si possono calcolare mediante il metodo dei moltiplicatori
di Lagrange, ossia risolvendo il sistema seguente nelle tre incognite x,
y
e λ:
F(x,y) = 0 ossiay = 0
∇g(x,y) = λ∇F(x,y)ossia g0′(x) = 0 ⋅ λ
0 = 1 ⋅ λ
La prima riga impone di limitarsi a considerare punti dell’asse delle ascisse.
Dall’ultima riga si vede che deve essere λ = 0.
La penultima impone di guardare i valori di x
per cui g0′(x) = 0.
Si ritrova quindi la condizione che la derivata prima deve annullarsi nei punti
estremi. _
Dimostrazione analitica del Teorema di Lagrange
Vediamo ora una dimostrazione analitica del metodo dei moltiplicatori di Lagrange,
che si presta a ulteriori generalizzazioni. Valgano le ipotesi del teorema e sia
(x0,y0) un punto di
estremo di g(x,y)
vincolato alla curva di livello
F(x,y) = c = F(x0,y0).
Dato che la funzione F(x,y)
è di classe C1
e che ∇F(x0,y0)≠0,
l’equazione F(x,y) = c
definisce una curva piana, in un opportuno intorno di
(x0,y0)
che si può esprime localmente mediante l’equazione
y = y(x) oppure
x = x(y).
Per fissare le idee supponiamo che valga la rappresentazione
y = y(x)
cosìche
Il punto (x0,y0) = (x0,y(x0))
è un punto di minimo vincolato per la funzione
g(x,y). Questo vuol dire
che esiste un intorno I
di x0 tale
che se x ∈ I
allora vale
F(x,y(x)) = 0,g(x0,y0) ≤ g(x,y(x)).
Imponendo che sia nulla la derivata prima di
g(x,y(x)) per
x = x0 si
trova
0 = dg(x0,y(x0))
dx = gx(x0,y0) + gy(x0,y0)y′(x
0).
Si ha quindi
|
0 = gx(x0,y0) + gy(x0,y0)y′(x
0).
| (5.12) |
Dal Teorema della funzione implicita si sa che
y′(x
0) = −Fx(x0,y0)
Fy(x0,y0).
Sostituendo in (5.12) si trova
gx(x0,y0) + − gy(x0,y0)
Fy(x0,y0) Fx(x0,y0) = 0.
Dunque, posto
λ = gy(x0,y0)
Fy(x0,y0),
si vede che
gx(x0,y0) = λFx(x0,y0).
Anche le derivate rispetto ad y
verificano l’uguaglianza analoga,
gy(x0,y0) = λFy(x0,y0),
col medesimo valore di λ.
Infatti,
gy(x0,y0) − λFy(x0,y0) = gy(x0,y0) + − gy(x0,y0)
Fy(x0,y0) Fy(x0,y0) = 0.
Ciò completa la dimostrazione.
5.5.2 Estremi vincolati ad una superficie
Siano F(x,y,z) e
g(x,y,z) due funzioni di
classe C1, definite
in un intorno U di
(x0,y0,z0). Supponiamo che
sia F(x0,y0,z0) = c. Si ricordi
che (x0,y0,z0) è punto
di minimo di g(x,y,z),
vincolato a F(x,y,z) = c
se
F(x,y,z) = cimplicag(x0,y0,z0) ≤ g(x,y,z).
La definizione si estende facilmente ai punti di massimo vincolato. Vale:
Teorema 176 Sia (x0,y0,z0)
un punto di minimo o di massimo, vincolato a
F(x,y,z) = c. Supponiamo che
il gradiente di F(x,y,z) non
si annulli in (x0,y0,z0). Allora
esiste un numero λ
per cui
|
λ∇F(x0,y0,z0) = ∇g(x0,y0,z0).
| (5.13) |
Dim. Studiamo il caso del punto di minimo. Per fissare le idee, supponiamo che sia
Fz(x0,y0,z0)≠0. Si espliciti
F(x,y,z) rispetto alla
variabile z. Il punto
(x0,y0,z0) è di minimo vincolato
alla condizione z − z(x,y) = 0,
ossia, la funzione
g(x,y,z(x,y))
ha minimo libero in (x0,y0).
Dunque, ambedue le sue derivate parziali sono nulle:
|
∂
∂xg(x0,y0,z(x0,y0)) = gx(x0,y0,z(x0,y0)) + gz(x0,y0,z(x0,y0))zx(x0,y0) = 0
∂
∂yg(x0,y0,z(x0,y0)) = gy(x0,y0,z(x0,y0)) + gz(x0,y0,z(x0,y0))zy(x0,y0) = 0.
|
Avendo supposto Fz(x0,y0,z0)≠0,
si ha
zx(x0,y0) = −Fx(x0,y0)
Fz(x0,y0),zy(x0,y0) = −Fy(x0,y0)
Fz(x0,y0)
ossia
|
gx(x0,y0,z0) + − gz(x0,y0,z0)
Fz(x0,y0,z0) Fx(x0,y0,z0) = 0
gy(x0,y0,z0) + − gz(x0,y0,z0)
Fz(x0,y0,z0) Fy(x0,y0,z0) = 0.
|
Naturalmente vale anche
gz(x0,y0,z0) + − gz(x0,y0,z0)
Fz(x0,y0,z0) Fz(x0,y0,z0) = 0.
Definendo
λ = −gz(x0,y0,z0)
Fz(x0,y0,z0)
si trova che vale la (5.13). _
5.5.3 Estremi vincolati ad una curva dello spazio
Sia F(r→) = F(x,y,z) una funzione
di classe C1 in
una regione Ω ⊆ ℝ3
e sia γ una
curva in Ω.
Vogliamo dare una condizione necessaria che deve valere se un punto
r→0 è punto di estremo
di F(r→) vincolato
alla curva γ.
Se la curva γ
è data in forma parametrica il probema si riduce immediatamente alla ricerca
degli estremi di una funzione di una sola variabile. Quindi consideriamo il caso in
cui γ
è data implicitamente, come intersezione di due superfici:
γ : g1(x,y,z) = c,g2(x,y,z) = d.
Sia r→0 = (x0,y0,z0) un punto di
γ, che è massimo
oppure minimo di F(r→)
vincolato a γ.
Supponiamo che in r→0
valga la condizione del teorema della funzione implicita. Privilegiando, per esempio, la
variabile x,
supponiamo che si abbia
|
det g1,y(x0,y0,z0)g1,z(x0,y0,z0)
g2,y(x0,y0,z0)g2,z(x0,y0,z0) ≠0.
| (5.14) |
Si ricordi che sotto questa condizione la curva
γ si rappresenta,
in un intorno di (x0,y0,z0),
in forma cartesiana, come
y = y(x),z = z(x)
e
y0 = y(x0),z0 = z(x0).
Dunque, la funzione della sola variabile
x
F(x,y(x),z(x))
ha un punto di estremo in x0
e quindi la sua derivata prima è ivi nulla:
0 = Fx(x0,y0,z0) + Fy(x0,y0,z0)y′(x
0) + Fz(x0,y0,z0)z′(x
0).
Usando questa condizione, si potrebbe provare il teorema seguente:
Teorema 177 Sia
r→0 = (x0,y0,z0)
punto di estremo della funzione
F(x,y,z)
vincolato alla curva
γ : g1(x,y,z) = c,g2(x,y,z) = d.
Valga inoltre la condizione (5.14). In tal caso esistono due numeri
λ1
e
λ2
tali che il punto
r→0 = (x0,y0,z0)
è punto estremale libero della funzione
F(x,y,z) + λ1g1(x,y,z) + λ2g2(x,y,z).
Ossia, nel punto (x0,y0,z0)
valgono contemporaneamente le condizioni seguenti:
|
g1(x0,y0,z0) = c,
g2(x0,y0,z0) = d,
Fx(x0,y0,z0) + λ1g1,x(x0,y0,z0) + λ2g2,x(x0,y0,z0) = 0,
Fy(x0,y0,z0) + λ1g1,y(x0,y0,z0) + λ2g2,y(x0,y0,z0) = 0,
Fz(x0,y0,z0) + λ1g1,z(x0,y0,z0) + λ2g2,z(x0,y0,z0) = 0.
|
La coppia (λ1,λ2) si
chiama ancora moltiplicatore di Lagrange (vettoriale) ed i due numeri si chiamano
moltiplicatori di Lagrange
5.5.4 Osservazione importante
Il metodo dei moltiplicatori di Lagrange dà condizioni necessarie che devono
essere soddisfatte da un punto di estremo vincolato, senza necessità di
esplicitare preventivamente l’equazione del vincolo. In ciascuno dei tre
casi esaminati, le condizioni possono scriversi come segue: si introduce la
funzione
L(r→) = F(r→) + λ ⋅ g(r→).
Nei primi due casi esaminati, λ
è un numero e g(r→)
è una funzione a valori reali; nell’ultimo caso
λ è un vettore a
due dimensioni, g(r) = g1(r→)g2(r→)
e il punto indica il prodotto scalare. In tutti i casi la ricerca del minimo o massimo vincolato di
F(r→) si riconduce alla ricerca
dei punti estremali di L(r→).
L’osservazione importante è questa: in generale gli estremi vincolati di
F(r→) sono solamente
punti estremali di L(r→).
Non sono nè punti di massimo n’e punti di minimo di
L(r→). La
funzione L(r→)
sopra introdotta si chiama lagrangiana del problema (di minimo, oppure di
massimo).
5.6 Appendice: la dimostrazione del teorema 165
La dimostrazione come conseguenza del Teorema della
funzione implicita. Come si è detto, consideriamo il caso
n = 2.
Scriviamo in componenti la relazione
x→ = (x,y) = F→(r→) = ϕ(u,v) ψ(u, v)
,r→ = (u,v) ∈ Ω′.
Ossia scriviamo quest’uguaglianza come
|
x = ϕ(u,v),y = ψ(u,v).
| (5.15) |
Vogliamo considerare questa come un sistema di equazioni nelle incognite
(u,v). Per
ipotesi si sa che
ϕ(u0,v0) = x0,ψ(u0,v0) = y0.
Si sa inoltre che ϕ(x,y)
e ψ(x,y) sono di
classe C1
e che
|
JF→(r→0) = ϕu(u0,v0)ψv(u0,v0) − ϕv(u0,v0)ψu(u0,v0)≠0.
| (5.16) |
Consideriamo la prima equazione in (5.15), che scriviamo come
|
0 = f(u,v,x) = ϕ(u,v) − x.
| (5.17) |
La (5.16) mostra che fu(u0,v0,x0) = ϕu(u0,v0)≠0
oppure fv(u0,v0,x0) = ϕv(u0,v0)≠0.
Sia per esempio
ϕu(u0,v0) = fu(u0,v0,x0)≠0.
In tal caso si può risolvere l’equazione (5.17) rispetto alla variabile
u ottenendo, in un
opportuno aperto W
contenente (u0,v0,x0),
|
u = U(v,x),U(v0,x0) = u0,ϕ(U(v,x),v) = x,
Uv(v0,x0) = −fv(u0,v0,x0)
fu(u0,v0,x0 = −ϕv(u0,v0)
ϕu(u0,v0).
|
Quando (u,v,x) ∈ W allora
si ha (v,x) ∈ H, aperto
contenente (v0,x0) ed
u appartiene ad
un intorno di u0.
Consideriamo ora l’equazione seguente, nell’aperto
H × ℝ:
0 = g(v,x,y) = ψ(U(v,x),v) − y.
Quest’uguaglianza è soddisfatta nel punto
(v0,x0,y0). Mostreremo
in seguito che gv(v0,x0,y0)≠0.
Accettando ciò, il teorema della funzione implicita mostra che l’equazione si può risolvere
rispetto a v, ottenendo
una funzione V (x,y)
di classe C1
v = V (x,y).
Questa uguaglianza vale per (v,x,y)
in un opportuno aperto K
contenente (v0,x0,y0) e
la funzione V (x,y)
è di classe C1.
Sostituendo v = V (x,y)
nell’uguaglianza u = U(v,x)
(si veda la (5.18)) si ottiene la soluzione del sistema (5.15)
u = U(V (x,y),x),v = V (x,y)
e, ricordiamo, le funzioni U(x,y)
e V (x,y) sono di
classe C1.
Vediamo ora quali restrizioni sono state imposte ai punti
(u,v) ed
(x,y).
Questi sono rappresentati dalle condizioni
(u,v,x) ∈ W,(v,x,y) ∈ H × ℝ,(v,x,y) ∈ K.
Si identifica così un aperto di ℝ4,
contenente il punto (u0,v0,x0,y0).
L’aperto A
detto nel teorema è la proiezione di quest’aperto sul piano
(u,v) mentre l’aperto
B è la proiezione
sul piano (x,y).
Per completare la dimostrazione, proviamo che
gv(v0,x0,y0)≠0. Usando
l’espressione di Uv(v0,x0)
in (5.18) si trova
|
gv(v0,x0,y0) = ψu(U(v0,x0),v0)Uv(v0,x0) + ψv(U(v0,x0),v0)
ψu(u0,v0) −ϕv(u0,v0)
ϕu(u0,v0) + ψv(u0,v0)
= 1
ϕu(u0,v0) ϕu(u0,v0)ψv(u0,v0) − ϕv(u0,v0)ψu(u0,v0)
= 1
ϕu(u0,v0)JF→(r→0)≠0.
|
Capitolo 6
Curve e superfici
Le curve e le superfici in forma implicita sono già state incontrate. In
questo capitolo studiamo le proprietà delle curve e delle superfici definite
parametricamente. Saremo precisi nella definizione di curva mentre le “superfici”
verranno definite in modo meno formale e preciso.
6.1 Curve parametriche
Conviene procedere per gradi nella definizione di curva. Una prima definizione, che
verrà resa più precisa in seguito, è la seguente: Una trasformazione continua da un
intervallo I
in ℝn
si chiama curva parametrica. Nella definizione di curva l’intervallo
può essere chiuso o meno, limitato o meno. Se però l’intervallo è
chiuso e limitato la curva si chiama un arco. Una curva a valori in
ℝ3 si
rappresenta in coordinate cartesiane nella forma
r→(t) = x(t)i→ + y(t)j→ + z(t)k→t ∈ I.
La curva si dice piana quando la sua immagine appartiene ad un piano di
ℝ3, ossia quando
esistono numeri a,
b,
c,
d, indipendenti
da t, tali che per
ogni valore di t
valga
ax(t) + by(t) + cz(t) = d.
Quando la curva è piana ed appartiene al piano
z = 0 essa
si rappresenta semplicemente come
r→(t) = x(t)i→ + y(t)j→.
Notazione analoga quando la curva appartiene agli altri piani coordinati. Una
curva si indica con una lettera greca minuscola:
γ : t →r→(t)t ∈ I.
In seguito noi ci limiteremo a considerare curve che hanno le seguenti proprietà di regolarità:
la funzione t →r→(t) è
derivabile su (a,b)
con l’eccezione di un numero finito di punti
ti. Si richiede che in questi
punti (ed anche in a
e in b
se l’intervallo è limitato) esistano i limiti direzionali di
r→′(t). Inoltre si
richiede che per t≠ti
si abbia r→′(t)≠0.
Una curva con tali proprietà si chiama regolare a tratti e si
parla di curva regolare quando essa è ovunque derivabile, con
r→′(t)≠0 per ogni
t. Sia
γ una curva
regolare e sia r→0 = r→(t0)
un punto della sua immagine. Una almeno delle componenti di
r→(t), per esempio la prima
componente x(t), è invertibile
in un intorno di t0. Dunque
l’immagine della restrizione di r→(t)
a tale intorno è anche immagine di una funzione di
x.
Si osservi che questo non implica che l’immagine di
r→(t)
debba essere grafico di funzione, perch’e niente possiamo dire nei punti di
t “lontani”
da t0.
Questo è illustrato dalla figura 6.1, a sinistra, che riporta l’immagine, diciamo
γ, della
funzione
|
(sin t)i→ + t(π2 − t2)j→,t ∈ [−π,π].
| (6.1) |
Si vede che quest’immagine non è grafico di funzione in nessun intorno di
(0, 0) nonostante che
la funzione x = sin t
sia invertibile. La sua inversa è
e quindi la relazione tra x
ed y è
la funzione
y = arc sin x π2 −arc sin x2 .
Il suo grafico è la parte spessa dell’immagine. Non esaurisce tutta la
γ perché i
valori di t
ottenuti da (6.2) sono solamente quelli dell’intervallo
[−π∕2,π∕2]. E’
appena il caso di notare che una curva, oltre che in coordinate cartesiane, può
rappresentarsi, per esempio, in coordinate polari.
Esempio 178 La curva
|
x = t cos t,y = t sin t,t > 0
| (6.3) |
rappresenta una spirale, si veda la figura 6.1 a destra. Essa può anche
rappresentarsi in coordinate polari, come
𝜃 = t,ρ = t,t > 0.
Consideriamo una curva piana. Questa si chiama curva cartesiana se è
rappresentata mediante una parametrizzazione della forma
t → ti→ + y(t)j→
oppure
t → x(t)i→ + tj→.
Più in generale, se t →r→(t)
è una curva in ℝn,
si dice che questa è una curva cartesiana quando una delle componenti della funzione
r→(t) ha la
rappresentazione xi(t) = t.
Un arco si dice chiuso quando una sua parametrizzazione
r→(t),
t ∈ [a,b] verifica
r→(a) = r→(b).
Una curva, oppure un arco, si dice semplice quando
r→(t′) = r→(t″) vale
solamente per t′ = t″
oppure se t′ = a,
t″ = b. L’interpretrazione
fisica del concetto di curva parametrica è suggerita dai problemi della meccanica: il parametro
t rappresenta il tempo
ed il punto r→(t) rappresenta
la posizione all’istante t
di un punto massa mobile nel tempo. Quest’interpretazione spiega la condizione di
continuità posta nella definizione di curva (un punto massa non fa salti). La funzione
t →r→(t)
si chiama in fisica la legge del moto e il vettore
r→′(t) rappresenta la velocità
del punto all’istante t.
Si noti che la velocità può essere discontinua, per esempio quando si verificano urti.
Introduciamo ora il “verso di percorrenza” su una curva parametrica semplice: Il parametro
t di una curva appartiene
ad un intervallo (a,b)
di ℝ e
ℝ è un
insieme ordinato. Dunque possiamo introdurre un ordine su una curva semplice
γ di parametrizzazione
r→(t) dicendo che il
punto r→(t′) viene
prima del punto r→(t″)
quando t′ < t″;
ossia quando un punto mobile sulla curva traversa prima
r→(t′) e poi
r→(t″). Si dice anche che,
in tal caso, il punto r→(t′)
precede r→(t″).
Nel caso che la curva sia semplice e chiusa, il punto
r→(a) coincide
col punto r→(b)
e quindi sfugge alla definizione data di ordine.
Osservazione 179 La definizione di curva parametrica è una definizione
soddisfacente per alcune applicazioni della fisica, ma non per tutte, ed è del
tutto insoddisfacente per la geometria. Infatti, privilegia un modo di misurare
il trascorrere del tempo. Ora, due orologi diversi possono segnare ore diverse
perché sono stati azzerati in istanti diversi e anche perché uno va più
velocemente dell’altro. Quindi il medesimo moto viene ad avere rappresentazioni
diverse, a seconda dell’orologio che si usa per descriverlo. Dobbiamo quindi
migliorare la definizione di curva, tenendo conto di ciò. Osservare una proprietà
cruciale del tempo: il tempo non si ferma e va in una sola direzione. Questo vuol
dire che se indico con τ
il tempo segnato da un orologio, al medesimo istante un secondo orologio
segnerà un diverso numero, diciamo t.
La corrispondenza che a τ
fa corrispondere t
è continua (perché il tempo non fa salti) e monotona strettamente crescente
(perché il tempo non si ferma e va in una sola direzione). Quest’osservazione
è la chiave per capire la definizione generale di curva che daremo al prossimo
paragrafo. _
6.1.1 I cambiamenti di parametro e la definizione di curva
Vogliamo ora completare la definizione di curva, tenendo conto delle ragioni esposte
nell’osservazione 179. Si dice che si cambia parametrizzazione della curva
γ quando si opera
la sostituzione t = t(τ)
purché la funzione τ → t(τ)
sia continua e strettamente crescente da un intervallo
J sull’intervallo
I. In
pratica noi assumeremo anche che questa trasformazione sia derivabile (e quindi che sia
t′(τ) ≥ 0).
Talvolta basterà supporre che la trasformazione sia derivabile a
tratti. Rendendo più precisa la definizione di curva, si dice che
r→(t),
t ∈ I e
r→̃(τ),
τ ∈ J
sono due diverse parametrizzazioni della stessa curva quando
r→̃(τ) = r→(t(τ)) con la funzione
τ → t(τ) strettamente
crescente e suriettiva.
Questa definizione corrisponde al concetto fisicamente intuitivo che una stessa
“curva” può descriversi con leggi orarie diverse. Sia ora
γ : t →r→(t),t ∈ (a,b)
e si consideri la trasformazione
t → b + a − t,t ∈ (a,b).
Questa trasformazione è monotona decrescente e quindi la curva di
parametrizzazione
t →r→(b − a − t),t ∈ (a,b)
è diversa dalla γ.
Intuitivamente, la seconda curva si ottiene “percorrendo la
γ
all’indietro”. Quando si effettua questa trasformazione sul parametro della curva, si dice
che “si è cambiato il verso di percorrenza della curva” e la curva cosìottenuta a partire
dalla γ
si indica col simbolo
Ora, alcune proprietà che dovremo studiare cambieranno al cambiare della
parametrizzazione, ossia della legge del moto. Altre non dipenderanno dalla
parametrizzazione. Le considereremo proprietà “geometriche” della curva.
Vediamo alcuni casi:
Teorema 180 Parametrizzazioni diverse della medesima curva hanno la
stessa immagine.
L’immagine comune a tutte le parametrizzazioni di una curva
γ si chiama il
sostegno di γ.
Dunque il sostegno è una proprietà geometrica della curva. Lo stesso dicasi della
proprietà di essere curva chiusa o curva semplice:
Teorema 181 Siano I
e J
due intervalli e siano r→(t),
t ∈ I,
r→̃(τ)
due curve parametriche. Sia t(τ)
una trasformazione strettamente monotona da J
in I,
suriettiva, tale che
r→̃(τ) = r→(t(τ)).
Allora, la curva parametrica
r→(t)
è chiusa se e solo se la curva parametrica
r→̃(τ)
lo è;
r→(t)
è semplice se e solo se
r→̃(τ)
lo è.
Ossia, le proprietà di essere chiusa, o di essere semplice, non dipendono dalla
particolare rappresentazione parametrica di una curva ma solo dalla curva stessa:
sono quindi proprietà geometriche della curva. E’ importante notare che le
proprietà appena dette non cambiano nemmeno cambiando il senso di percorrenza
della curva. Ossia:
La curva
γ
e la curva
−γ
hanno il medesimo sostegno. L’una è
- semplice
- chiusa
- semplice e chiusa
se e solo se l’altra lo è.
Inoltre,
Teorema 182 l’ordine sulla curva non muta cambiando parametrizzazione.
E’ proprio per ottenere ciò che si è imposto che i cambiamenti
di parametro debbano essere strettamente crescenti. L’ordine su
−γ è invece l’opposto
di quello su γ. Quando
la trasformazione t(τ)
da un intervallo J
su un intervallo I
è continua e strettamente monotona (crescente o meno) allora
I è sia limitato che
chiuso se e solo se J
lo è. Dunque diremo che una curva è un arco quando una sua
parametrizzazione è definita su un intervallo limitato e chiuso: la proprietà
di essere un arco è una proprietà geometrica della curva e non cambia
cambiando verso di percorrenza sulla curva, ossia essa è comune sia a
γ che a
−γ.
invece, dipendono dalla parametrizzazione sia la velocità
r→′(t) che la
proprietà di essere una curva cartesiana. Si consideri ora l’esempio seguente:
Esempio 183 le due curve
t → (cos t)i→ + (sin t)j→,t ∈ (0, 2π]et → (cos t)i→ + (sin t)j→,t ∈ (0, 4π)
hanno il medesimo sostegno (la circonferenza x2 + y2 = 1).
Le due parametrizzazioni però non possono ricondursi l’una all’altra mediante
un cambiamento di parametro (che deve essere strettamente crescente) perché
la prima curva è semplice e l’altra non lo è. _
Gli archi semplici
hanno molte proprietà importanti. Tra queste:
Teorema 184 Sia
γ : t →r→(t),t ∈ (a,b)
un arco semplice (chiuso o meno). Esiste soltanto un diverso arco che ha il
medesimo sostegno, e questo è l’arco −γ.
Grazie a questo risultato, trattando di archi semplici, possiamo
usare un linguaggio più informale: se si sa che un insieme
S
è sostegno di un’arco semplice, possiamo parlare di “arco
S” intendendo uno dei
due archi che hanno S
per sostegno. In generale si intende anche di aver fissato un verso di percorrenza su
S, e in
tal caso si sceglie quello dei due archi che corrisponde a tale verso. Per esempio,
sia
S = {(x,y,z)|x2 + y2 + z2 = 1,x + y + z = 0}.
L’insieme S
è una circonferenza nello spazio. Possiamo parlare dell’“arco
S” intendendo implicitamente
di considerare S
come sostegno di un arco semplice e di scegliere una qualsiasi delle parametrizzazioni
che corrispondono a tale arco. Se si stabilisce un verso di percorrenza su
S,
si viene a scegliere uno solo dei due archi che hanno
S per
sostegno. Si noti però che in generale non esiste un modo unico per la scelta del
verso di percorrenza e quindi questo linguaggio informale non identifica
univocamente l’arco. Vedremo che questa diffcoltà si risolve nel caso delle curve
semplici e chiuse.
6.1.2 Lunghezza di un arco
Studiamo il problema di definire un numero che rappresenti la “lunghezza” di un arco
in ℝn.
Consideriamo per questo un arco (che indichiamo col simbolo
γ) di
parametrizzazione t →r→(t),
t ∈ [a,b]. Si sa che la tangente al
grafico della funzione t →r→(t)
nel punto (t0,r→(t0))
ha equazione
r→ = r→(t0) + r→′(t
0)(t − t0).
Dividiamo l’intervallo [a,b]
mediante i punti tn, equidistanti,
t0 = a,…,tN = b
e approssimiamo l’arco con tanti segmenti di tangente, si veda la figura 6.2: l’arco
r→(t),
t ∈ [ti,ti+1] si
approssima mediante il segmento di tangente
r→(t0) + r→′(t
0)(t − t0),t ∈ [ti,ti+1].
Sommiamo le lunghezze dei singoli segmenti di tangente. Ripetendo questo procedimento per
ogni N si costruisce una
successione di numeri (LN).
Se esiste L = lim LN, si sceglie
questo numero L come
“lunghezza” dell’arco γ.
Più precisamente, supponiamo che la funzione
r→(t) sia di
classe C1
e supponiamo che essa ammetta le derivate direzionali finite in ambedue gli estremi
a e
b.
Per definire la lunghezza del’arco, si divide l’intervallo
[a,b] in
N parti uguali
mediante i punti kT
N ,
0 ≤ k < N e
T = b − a. Il segmento di tangente
al grafico nel punto (kT
N ,r→(kT
N ))
ottenuto per t ∈ (kT
N , (k+1)T
N )
ha lunghezza
r→′kT
N ⋅ T
N.
La lunghezza totale dei segmenti di tangente è il numero
LN = ∑
k=0N−1 r→′kT
N ⋅ T
N.
Se esiste, il numero L = lim LN è
l’integrale della funzione r→′(t)
sull’intervallo [a,b].
Dunque, definiamo la lunghezza dell’arco ponendo
|
Lγ = ∫
ab r→′(t) dt.
| (6.5) |
Osservazione 185 Al numero L
siamo giunti scegliendo di dividere l’intervallo [a,b]
in parti uguali. Non è diffcile mostrare che allo stesso numero L
si perviene considerando una qualsiasi partizione di [a,b],
la cui finezza tende a zero. Ci si può chiedere però a quale numero si giunge
se, invece di “approssimare” il grafico con segmenti di tangente, si sceglie di
approssimarlo con segmenti di secante. E’ possibile provare che si giunge al
medesimo numero L,
dato da (6.5). _
Teorema 186 La lunghezza di un arco non muta cambiando
parametrizzazione.
Dim. Sia t = t(τ) una trasformazione
crescente da [α,β] su
[a,b]. Sia inoltre essa ovunque
derivabile cosìche t′(τ) ≥ 0.
Sia r→̃(τ) = r→(t(τ)).
La regola di cambiamento di variabile mostra che
|
L = ∫
ab d
dtr→(t) dt = ∫
αβ d
dtr→(t(τ)) t′(τ)dτ
= ∫
αβ d
dtr→(t(τ))t′(τ) dτ = ∫
αβ d
dτr→̃(τ) dτ.
|
Dunque, il numero che esprime la lunghezza di un arco è una proprietà geometrica
dell‘arco. Vale inoltre:
Teorema 187 La lunghezza di un arco non muta cambiando il verso di
percorrenza sulla curva. Ossia:
Lγ = L−γ.
Dim. Infatti, se t′(τ) < 0
allora
∫
ab d
dtr→(t) dt = ∫
βα d
dtr→(t(τ)) t′(τ)dτ = ∫
αβ d
dtr→(t(τ)) (−t′(τ))dτ
e −t′(τ) = |t′(τ)|.
Dunque anche in questo caso vale
L = ∫
αβ d
dtr→(t(τ))t′(τ) dτ = ∫
αβ d
dτr→̃(τ) dτ.
Osservazione 188
- Un’interpretazione della formula (6.5) è la seguente: la parametrizzazione
t →r→(t)
si intende come legge del moto di un punto che percorre la curva. Allora,
r→′(t)
è il vettore velocità del punto mobile all’istante t.
La (6.5) si interpreta dicendo che l’integrale del modulo della velocità dà
la lunghezza del cammino percorso.
- Sia γ
una curva cartesiana, ossia
γ : r→(t) = ti→ + f(t)j→.
In questo caso,
|
r→′(t) = i→ + f′(t)j→,|r→(t)| = 1 + [f′ (t)]2.
| (6.6) |
La lunghezza dell’arco ottenuto quando
t ∈ [a,b]
è quindi data da
Lγ = ∫
ab1 + [f′ (t)]2dt.
Definiamo ora la funzione s(t)
s(t) = ∫
at r→′(ν) dνt ∈ [a,b].
Se l’arco γ è
regolare, s′(t) > 0 per
ogni t. Ossia la
trasformazione t → s(t)
da [a,b] su
[0,L] è un cambiamento di
parametro per l’arco γ.
Il numero s ∈ [0,L]
si chiama per questo il parametro d’arco. Se come parametro di
γ si sceglie
s si trova una nuova
parametrizzazione dell’arco γ,
che indichiamo con r→(s)
e che si chiama la parametrizzazione canonica dell’arco. La sua proprietà
importante è che
d
dsr→(s) = 1.
Infatti, essendo s(ν) la
funzione inversa di ν(s),
si ha:
|
d
dsr→(s) = d
dsr→(ν(s)) = d
dνr→(ν(s)) ν′(s)
= d
dνr→(ν(s)) 1
s′(ν(s)) = d
dνr→(ν(s)) 1
|(d∕dν)r→(ν(s))|.
|
Dunque, quando la curva è data mediante la sua parametrizzazione canonica,
la formula per la lunghezza si riduce a:
L = ∫
0L1ds.
Il parametro d’arco si presta allo studio delle proprietà geometriche delle curve. Però
la parametrizzazione mediante il parametro d’arco è spesso piuttosto complicata e
spesso non si presta a fare calcoli concreti. Concludiamo dicendo che in fisica la
funzione s = s(t)
si chiama legge oraria del moto.
6.1.3 Proprietà differenziali delle curve piane e dello spazio
Studiamo prima di tutto il caso delle curve piane. Supponiamo che l’arco
γ sia
parametrizzata dalla sua lunghezza,
γ : s →r→(s),s ∈ [0,L]
e supponiamo che sia regolare a tratti; ossia che la funzione
s →r→(s)
sia ovunque continua; inoltre supponiamo che essa sia derivabile, con
|r→′(s)|≠0 su
[0,L],
con la possibile eccezione di un numero finito di valori
s1,…,sk
di s. In tali punti richiediamo
che esistano finiti i limiti
direzionali i limiti direzionali di r→′(s).
Il versore
t→(s) = d
dsr→(s)
applicato nel punto r→(s)
si chiama il versore tangente alla curva nel punto
r→(s).
Il versore tangente è definito salvo che in un numero finito di valori di
s. Per ogni
s nel quale
t→(s) è definito, introduciamo
il versore n→(s) ortogonale
a t→(s) e diretto in modo
tale che la coppia (t→(s),n→(s))
sia orientata positivamente (ossia, possa sovrapporsi ordinatamente ai versori
i→ e
j→ degli
assi coordinati mediante una rotazione e una traslazione di assi). Il versore
n→(s) si chiama il versore
normale alla curva γ.
Vale:
Teorema 189 Sia γ
una curva regolare, la cui parametrizzazione è di classe C2.
Allora il vettore n→(s)
è derivabile e in ogni punto è colineare col vettore t→′(s).
Dim. Infatti, ||t→(s)|| = 1
per tutti gli s
e quindi t→(s) ⋅t→′(s) = 0 per
ogni s. Dunque,
n→(s) = ± t→′(s)
||t→′(s)||. Ciò mostra che
per ogni valore di s
i due vettori t→(s) ed
n→(s) sono colineari. fissiamo
ora un valore s0 in cui
r→(s) ammette derivata
continua e supponiamo
che sia n→(s0) = + t→′(s0)
||t→′(s0)||.
Ciò vuol dire che
det t→(s0) + t→′(s0)
||t→′(s0)|| > 0.
Per continuità, la disuguaglianza si conserva in un intorno di
s0 e ciò mostra che
in un intorno di s0
vale
n→(s) = + t→′(s)
||t→′(s)||.
Il denominatore non si annulla e quindi
n→(s) è
derivabile. _
Osservazione 190 Si ricordi che la derivata del versore
t→(s)
è il limite del rapporto incrementale
t→(s + h) −t→(s)
h ,
applicato in r→(s). _
Supponiamo ora di lavorare con parametrizzazioni di classe
C2 di curve regolari,
e studiamo t→′(s).
Si è visto nella dimostrazione del Teorema 189, che
t→′(s) è parallelo al
versore n→(s). Esiste
quindi un numero k(s)
tale che
|
t→′(s) = k(s)n→(s).
| (6.7) |
Il numero k(s),
che può essere positivo o negativo, si chiama la curvatura di
γ nel
punto r→(s).
Prendendo la norma dei vettori ai due membri di (6.7) si trova
|k(s)| = ||t→′(s)||.
L’esempio seguente mostra che la curvatura può cambiare segno da punto a punto
di una medesima curva; e mostra anche che per calcolare tangenti, normali e
curvatura non è necessario parametrizzare preventivamente la curva col parametro
d’arco.
Esempio 191 Sia
r→(x) = (x,f(x))
cosìche
ds(x)
dx = 1 + f′ 2 (x).
Dalla formula per la derivata della funzione inversa
t→(s) = dr→(s)
ds = →dr(x(s))
dx x′(s) = 1
1 + f′ 2 (s) d
dx 1
1 + f′ 2 (x)(1,f′(x)) .
Dunque,
|
dt→(x)
ds = 1
1 + f′ 2 (x) d
dx (1,f′(x))
1 + f′ 2 (x)
1
1 + f′ 2 (x) 1
1 + f′2(x) (0,f″(x))1 + f′ 2 (x) − (1,f′(x)) f′(x)f″(x)
1 + f′ 2 (x)
= f″(x)
(1 + f′2(x))2(−f′(x), 1) = k(x) 1
1 + f′ 2 (x)(−f′(x), 1).
|
Si trova da qui
k(x) = f″(x)
(1 + f′2(x))3∕2.
La curvatura ha quindi il segno di f″(x).
Si confronti con la definizione di curvatura data al par. 6.3 del testo di Analisi
Matematica 1. _
Osserviamo ora che t→(s) ⋅n→(s) = 0
e quindi, derivando,
|
0 = t→′(s)⋅n→(s)+t→(s)⋅n→′(s) = k(s)n→(s)⋅n→(s)+t→(s)⋅n→′(s) = k(s)+t→(s)⋅n→′(s).
| (6.8) |
D’altra parte, n→′(s)
è ortogonale ad n→(s)
(perch’e ||n→(s)|| = 1)
e quindi
n→′(s) = α(s)t→(s).
Sostituendo nella (6.8) si vede che α(s) = −k(s).
Ne viene che le due funzioni t→(s)
ed n→(s)
risolvono il sistema di equazioni differenziali
|
t→′(s) = k(s)n→(s),n→′(s) = −k(s)t→(s).
| (6.9) |
Queste equazioni si chiamano Equazioni di Frenet per le
curve piane. Il sistema di riferimento dato dai due versori
t→(s),
n→(s)
(in quest’ordine) applicati nel punto r→(s)
si chiama il riferimento mobile sulla curva. La figura 6.3 illustra il riferimento
mobile nel caso in cui la curva venga percorsa in due versi opposti.
Studiamo ora il caso delle curve di
ℝ3. Intendiamo
ancora che la curva sia parametrizzata dal parametro d’arco. La definizione del versore
tangente t→(s)
è ancora
t→(s) = d
dsr→(s).
Invece, la curvatura deve essere trattata in modo diverso. Assegnato il vettore
t→(s) tangente alla
curva γ e di
modulo 1, è
ancora vero che t→′(s)
è ortogonale a t→(s).
Dunque privilegeremo, tra le infinite direzioni normali a
t→(s), la direzione
di t→′(s);
ma non c’è alcun modo di privilegiare un verso su tale direzione. Dunque
decidiamo di scegliere come versore normale il versore
|
n→(s) = t→′(s)
||t→′(s)||.
| (6.10) |
Chiamiamo questo il versore normale alla curva
γ. Chiamiamo
curvatura il numero k(s)
tale che
t→′(s) = k(s)n→(s)ossiak(s) = ||t→′(s)|| = t→′(s) ⋅n→(s).
In questo modo,
k(s) ≥ 0∀s.
Osservazione 192 Se una curva regolare è piana, il suo versore normale
è ovunque definito. Invece, una curva nello spazio potrebbe essere priva di
versore normale su tutto un arco o addirittura ovunque. Ciò avviene se
t→′(s)
è nullo. In particolare, può accadere che
t→′(s)
sia identicamente zero su un intervallo. In questo caso, l’arco corrispondente
è piano, parametrizzato da
r→(s) = sr→0 + r→1.
La definizione di versore normale data in
ℝ3
non si applica in questo caso. _
6.2 Curve piane
E’ importante sapere che vale il teorema seguente, di enunciato del tutto intuitivo
ma di dimostrazione molto complessa:
Teorema 193 (teorema di Jordan) Sia
γ
una curva piana chiusa e semplice. Il complementare del sostegno di
γ
è unione di due regioni. Una di esse è illimitata (e si dice esterna alla curva)
mentre l’altra è limitata e si dice la regione interna alla curva.
Il teorema è illustrato nella figura 6.4, a sinistra.
Il sostegno di γ
è la frontiera sia della regione interna che della regione esterna di
γ (si
veda il paragrafo 3.3 per la definizione di frontiera).
Esempio 194 La curva
x = 3 cos 𝜃,y = 2 sin 𝜃
ha per sostegno un’ellisse. La sua regione interna è la parte di piano
delimitata dall’ellisse. La regione esterna è quella dei punti che “stanno fuori”
dall’ellisse. _
Ovviamente, non esiste alcun “teorema di Jordan” per curve dello spazio! Usa chiamare
regione di Jordan la regione interna ad una curva piana semplice e chiusa. Se
γ indica la curva,
conviene indicare con Ωγ
la sua regione interna. Vale:
Teorema 195 Sia
γ
una curva semplice e chiusa. E’:
Ωγ = Ω−γ.
La regione interna ad una curva piana semplice e chiusa può essere assai
complicata; ma nella maggior parte dei casi che si incontrano nelle applicazioni
sarà facile identificarla. Nel paragrafo 6.1 abbiamo usato l’ordinamento su
ℝ
per definire un ordine sulla curva γ.
Nel par. 3.2.1 abbiamo notato che il piano può venire
orientato con la regola seguente: la coppia dei vettori
v→
e w→
applicati in O
e presi in quest’ordine, è orientata positivamente quando la semiretta identificata
da v→
deve ruotare in verso antiorario per portarsi su quellaidentificata da
w→,
percorrendo l’angolo minore possibile. Si veda la figura 6.5 a
sinistra. Questa definizione può anche riformularsi mediante la
regola d’Ampère: una persona stando in piedi nell’origine del piano
xy
con la testa nel verso positivo dell’asse delle quote vede la semiretta muoversi in
verso antiorario, e quindi la vede passare dalla sua destra alla sua sinistra.
Sia ora γ
una curva piana semplice e chiusa. Ricordiamo che il suo sostegno è sostegno, oltre che di
γ, soltanto della
seconda curva −γ,
che si ottiene “andando all’indietro”. Diciamo che
γ è orientata in
modo concorde a ℝ2,
o anche che è orientata positivamente, se vale la regola d’Ampère: una persona in
piedi in un punto della regione interna alla curva, stando in piedi come l’asse delle quote
positivo, vede un punto mobile sulla curva passare dalla sua destra alla sua sinistra. In
modo equivalente, si può anche dire che un insetto che segue il punto mobile su una
curva semplice e chiusa vede la regione interna alla sua sinistra, si veda la
figura 6.5 a destra. Altrimenti, diciamo che è orientata negativamente. Vale:
Teorema 196 Delle due curve semplici e chiuse, γ
e −γ,
una è orientata positivamente e l’altra è oreintata negativamente.
Supponiamo ora che la curva piana semplice e chiusa
γ
sia anche regolare, cosìche si possono definire sia il vettore tangente
t→(s) che il vettore
normale n→(s). Il
vettore normale n→(s)
può puntare sia verso la regione interna che verso la regione esterna alla curva. Per
il seguito avremo bisogno del vettore normale che punta verso la regione esterna alla
curva γ
(si veda la figura 6.4, a destra). Lo indicheremo col simbolo
n→e→(s)
e lo chiameremo la normale esterna.
Osservazione 197 Al paragrafo 6.1.3 si è definito il vettore n→(s)
come il vettore normale a t→(s),
orientato in modo tale che la coppia ordinata (t→(s),n→(s))
costituisca un sistema di riferimento positivo. Dunque n→(s)
punta verso la sinistra di t→(s).
Quando la curva è orientata positivamente, allora n→(s)
punta verso la regione interna alla curva. Quindi, in questo caso si ha n→(s) = −n→e(s). _
Torniamo ad usare il fatto che il sostegno di una curva semplice e chiusa è sostegno
anche di una seconda curva, che si ottiene dalla prima “girando in verso opposto”.
Quest’osservazione permette di introdurre un linguaggio più informale, che
tuttavia è limitato alle curve piane. Supponiamo che si sappia che un certo
insieme del piano è il sostegno di una curva semplice e chiusa. Per esempio un
quadrato o una circonferenza. Invece di scrivere esplicitamente la parametrizzazione
della curva, possiamo indicare il sostegno e implicitamente intendere di scegliere quella
curva semplice che ha il sostegno dato e che è orientata positivamente, senza
dover esplicitamente scrivere una sua parametrizzazione. In particolare, se
Ω
è la regione interna ad una curva semplice e chiusa
γ, e se
vogliamo che γ
sia orientata positivamente, potremo semplicemente indicarla come “frontiera di
Ω”,
∂Ω.
Osservazione 198 Con questa convenzione, se γ
è un sostegno di curva semplice e chiusa, si indica con γ
(o, per ridondanza, +γ)
la curva semplice e chiusa che ha il dato sostegno e che è orientata positivamente,
e con −γ
quella che ha il dato sostegno ed è orientata negativamente. _
6.3 Le superfici
Studiamo ora le superfici in ℝ3.
Considerazioni analoghe a quello che hanno condotto a definire prima le curve
parametriche e poi le curve come “oggetti geometrici” si possono ripetere per le
superfici. Però sono alquanto complesse e quindi ci limiteremo a definire le
superfici parametriche, mostrando quando certe proprietà che ci interessano sono
indipendenti dalla parametrizzazione scelta.
6.3.1 Superfici definite parametricamente
Nel definire le curve è stato naturale partire da funzioni continue definite
su intervalli. Per definire le superfici dobbiamo considerare funzioni
continue di due variabili, definite quindi su un dominio contenuto in
ℝ2.
richiederemo che il dominio sia una regione. Una funzione continua
|
r→(u,v) = x(u,v)i→ + y(u,v)j→ + z(u,v)k→
| (6.11) |
il cui dominio è una regione di Ω
si chiama una superficie definita parametricamente. L’immagine della funzione
r→(u,v)
si chiama il sostegno della superficie mentre il punto
(u,v) variabile
in Ω si
chiama il parametro della superficie. Una superficie si dice semplice quando valori
diversi del parametro hanno per immagine punti diversi del sostegno. Una
superficie si dice chiusa quando il suo sostegno è la frontiera di una regione di
ℝ3.
Sia
Σ : (u,v) → x(u,v)i→ + y(u,v)j→ + z(u,v)k→
una superficie. Diremo che la superficie è regolare quando la trasformazione (6.11) è
di classe C1
e inoltre la matrice jacobiana della trasformazione
|
xu(u,v)xv(u,v)
yu(u,v)yv(u,v)
zu(u,v)zv(u,v)
| (6.12) |
ha rango 2,
ossia il massimo possibile, in ogni punto della regione
Ω.
Cosìcome nel caso delle curve, una stessa superficie può parametrizzarsi in più
modi. Senza entrare in eccessivi dettagli, diremo che una trasformazione
α β →u(α,β) v(α, β)
è un cambiamento di parametro quando è definita su una regione
Ω ̃, a valori in
Ω; è iniettiva e suriettiva;
è di classe C1 e inoltre
conserva l’orientazione di ℝ2,
ossia il suo jacobiano è positivo in ogni punto:
det uα(α,β)uβ(α,β)
vα(α,β)vβ(α,β) > 0.
Si noti l’analogia con la nozione di cambiamento di parametro
per una curva. Anche nel caso delle curve il cambiamento di
parametro deve conservare l’orientazione, in tal caso l’orientazione di
ℝ.
E’ ovvio che cambiando parametro non si cambia il sostegno di una
superficie. Diremo equivalenti, e le identificheremo, due superfici che
differiscono solamente per la parametrizzazione. Le funzioni definite su
Ω, a valori
in ℝ3,
sono particolari superfici, rappresentate da
Σ : (x,y) → xi→ + yj→ + z(x,y)k→.
Esse si chiamano superfici cartesiane. Il sostegno in questo caso è il grafico della funzione
z(x,y). Sia ora
ΩΓ una regione di
Jordan e sia r→(u,v)
una funzione continua sull’insieme chiuso costituito dall’unione della regione
ΩΓ e del supporto
di Γ. In tal caso
la funzione r→(u,v)
si chiama calotta Ovviamente, la restrizione di
r→(u,v) ad
ΩΓ è una
superficie. Conviene estendere la definizione di calotta in questo modo. Siano date, oltre alla
Γ, anche le curve
di Jordan γ1,
γ2,…,
γn i cui
sostegni non si intersecano. Supponiamo che ciascuna di queste curve abbia sostegno in
ΩΓ. Indichiamo
con K
l’insieme chiuso i cui punti sono quelli del sostegno di
Γ e della sua
regione interna ΩΓ,
esclusi i punti della regione interna a ciascuna
γi (e quindi inclusi i punti
dei sostegni delle γi).
La figura 6.6 mostra in tratteggio un esempio di insieme
K.
Se la funzione r→(u,v)
in (6.11) è continua su K
essa si chiama calotta. Si chiama sostegno della calotta l’immagine della funzione
r→(u,v). L’insieme dei
punti interni di K
è ancora una regione (anche se non più una regione di Jordan) e quindi la restrizione
di r→(u,v)
a tale insieme è una superficie. Parleremo di calotta chiusa
se accade che la calotta è frontiera di un insieme aperto di
ℝ3.
Osservazione 199 Non si confonda il concetto di “insieme chiuso” con quello
di “superficie chiusa” o di “calotta chiusa”. La calotta di parametrizzazione
x = u,y = v,z = u + v
definita sul disco
u2 + v2 ≤ 1
ha per sostegno un insieme chiuso; ma la calotta stessa è contenuta nel piano
z = x + y
e quindi non è una calotta chiusa. _
Una superficie, oppure una calotta, si indica con una lettera greca maiuscola, come per
esempio Σ
o Γ.
Il concetto seguente è molto delicato e noi ci limitiamo a darne
una definizione grossolana. Supponiamo di avere una calotta
Σ
r→(u,v) = x(u,v)i→ + y(u,v)j→ + z(u,v)k→,(u,v) ∈ K.
Supponiamo che la calotta sia semplice ossia che
x(u′,v′) = x(u,v),y(u′,v′) = y(u,v),z(u′,v′) = z(u,v)
possa aversi solo se u = u′
e v = v′.
In tal caso si chiama bordo della calotta
Σ
l’immagine della frontiera dell’insieme K;
ossia l’immagine delle singole curve che delimitano l’insieme
K.
La figura 6.7 mostra una calotta e il suo bordo.
Esempio 200 Si è detto che la definizione di bordo è insoddisfacente.
Quest’esempio ne mostra la ragione. Consideriamo la calotta definita come segue. La
funzione r→(𝜃,v)
è
|
Σ : x = cos 𝜃,y = sin 𝜃,z = v.
| (6.13) |
Il dominio della funzione è
0 ≤ v ≤ 1,𝜖 ≤ 𝜃 ≤ 2π
con 𝜖 > 0.
Si tratta di un cilindro a cui è stata tolta una striscetta, come in figura 6.8.
Questa calotta è una calotta semplice e il suo bordo è costituito
dai due archi di circonferenza (archi della circonferenza di sopra
e di quella di sotto, alle quali è tolto l’arco che corrisponde a
0 < 𝜃 < 𝜖)
e dai bordi del taglio che le congiungono. Supponiamo ora di mandare
𝜖 a
zero. In tal caso si trova un cilindro intero. La sua parametrizzazione non è più
semplice, e quindi non possiamo più parlare di “bordo” secondo la nostra definizione,
anche se appare naturale considerare le due circonferenze come il bordo del cilindro.
Mentre il contributo dei due bordi del taglio “scompare”. Quest’esempio mostra che
dovremmo dare un modo per definire il “bordo” anche per calotte che non
sono semplici. Per esempio anche nel caso del cilindro ottenuto scegliendo
𝜃 ∈ [0, 2π]. La
soluzione ovvia è quella di scegliere come bordo l’immagine della frontiera dell’insieme
K,
in quest’esempio l’immagine del perimetro del rettangolo
[0, 1] × [0, 2π].
In questo modo si otterrebbe come bordo l’insieme delle due
circonferenze ed anche il segmento verticale dei punti di coordinate
(1, 0,v),
0 ≤ v ≤ 1.
Questa soluzione però non è accettabile. Infatti lo stesso cilindro si parametrizza
anche scegliendo come dominio della funzione (6.13) l’insieme
0 ≤ v ≤ 1, − π ≤ v ≤ π
e con questa parametrizzazione si trova un’altro insieme come “bordo”: l’insieme
costituito dalle due circonferenze e dal segmento dei punti (−1, 0,v),
0 ≤ v ≤ 1.
Ossia, il bordo cosìdefinito viene a dipendere dalla particolare parametrizzazione
che si sceglie. Ci sono vari modi per risolvere questa diffcoltà: uno, più
astratto, consiste nel considerare tutte le parametrizzazioni della calotta, ciascuna
definita su un proprio insieme K.
Si considerano quindi le immagini di tutte le frontiere di questi insiemi K
e se ne fa l’intersezione. Noi seguiremo una via “più concreta” che si adatta
ai casi semplici che incontreremo nelle applicazioni e che sarà illustrata al
paragrafo 8.5.2. _
6.3.2 Il piano tangente e la normale a una superficie
Sia
Σ : (u,v) → x(u,v)i→ + y(u,v)j→ + z(u,v)k→(u,v) ∈ Ω
una superficie regolare e semplice. fissiamo l’attenzione su un punto
r→0 del
sostegno. Dato che la superficie è semplice, questo proviene da un unico punto
(u0,v0) del
dominio:
u→0 = (u0,v0),r→0 = x(u0,v0)i→ + y(u0,v0)j→ + z(u0,v0)k→.
Consideriamo ora il segmento per u→0,
parallelo all’asse delle ascisse, ossia la curva
γ : t → (u0 + t,v0)
Questo identifica una curva sulla superficie, parametrizzata da
t → x(u0 + t,v0)i→ + y(u0 + t,v0)j→ + z(u0 + t,v0)k→.
La tangente a questa curva calcolata per
t = 0, ossia in
r→0, è identificata
dal vettore v→1
(applicato in r→0)
|
v→1 = xu(u0,v0)i→ + yu(u0,v0)j→ + zu(u0,v0)k→.
| (6.14) |
Analogamente, considerando un segmento per
u→0
parallelo all’asse delle ordinate, si trova una curva sulla superficie, la cui tangente in
r→0 è identificata
dal vettore v→2
(applicato in r→0):
|
v→2 = xv(u0,v0)i→ + yv(u0,v0)j→ + zv(u0,v0)k→.
| (6.15) |
In generale, il segmento
t → (u0 + at,v0 + bt)
identifica una curva sulla superficie, il cui vettore tangente è identificato dal
vettore
av→1 + bv→2(applicato in r→0).
I vettori v→1 e
v→2 dipendono
da (u0,v0):
v→1(u0,v0),v→2(u0,v0)
e sono le due colonne della matrice jacobiana (6.12) e quindi sono linearmente
indipendenti (infatti abbiamo assunto che la superficie sia regolare). Dunque al variare
di a e
di b in
ℝ, i vettori
av→1 + bv→2 applicati in
r→0 = r→(u0,v0) descrivono un
piano per r→0,
che si chiama il piano tangente alla superficie nel punto
r→0. Si
noti esplicitamente che intendiamo di scegliere come sistema di riferimento
cartesiano (in generale, obliquo) in questo piano le rette identificate al vettore
v→1(u0,v0) per primo
e quindi v→2(u0,v0).
E’ su questi assi cartesiani si sceglie per verso positivo quello dei rispettivi vettori.
Dunque sul piano tangente è definita un’orientazione. Definiamo ora il vettore normale
N→(u0,v0)
ponendo
N→(u0,v0) = v→1(u0,v0) ∧v→2(u0,v0).
Il vettore N→(u0,v0) si intende
applicato nel punto r→0 = r→(u0,v0).
E’ ovvio:
Teorema 201 Se la superficie semplice Σ
è regolare, sia i vettori v→1(u0,v0),
v→2(u0,v0)
che il vettore normale N→(u0,v0)
dipendono con continuità da (u0,v0).
Si ricordi che la superficie si è supposta semplice. Quindi ogni
r→0
proviene da un unico punto (u0,v0) ∈ Ω.
Dunque in ogni punto di una superficie regolare e semplice il vettore normale
N→
sopra definito è unico e questo vettore si potrà
considerare come funzione del punto della superficie:
N→ = N→(r→).
Si è cosìdefinito un campo vettoriale sulla superficie. I concetti appena
esposti sono illustrati nella figura 6.9.
Se la superficie è cartesiana si ha:
v→1(x0,y0) = 1 0
zx(x0,y0) ,v→2(x0,y0) = 0 1
zy(x0,y0) N→(x0,y0) = −zx(x0,y0)
−zy(x0,y0)
1 .
Per il seguito è importante ricordare la formula per
||N→(r→)|| nel
caso di una superficie cartesiana: |
||N→(x0,y0)|| = 1 + [zx (x, y)]2 + [zy (x, y)]2.
| (6.16) |
Si confronti questa formula con la (6.6). Studiamo ora come cambiano i vettori
v→1(u0,v0),
v→2(u0,v0) e il
vettore N→(u0,v0)
sotto l’azione dei cambiamenti di parametro. Sia
u = u(t,s),
v = v(t,s) una trasformazione
biunivoca (e di classe C1)
da una regione Ω′
su Ω e
consideriamo la parametrizzazione
r→(t,s) = x(u(t,s),v(t,s))i→ + y(u(t,s),v(t,s))j→ + z(u(t,s),v(t,s))k→.
Le derivate rispetto ad t
ed s si
calcolano mediante la regola di derivazione a catena. Poniamo:
a = ut(t,s),b = vt(t,s),c = us(t,s),d = vs(t,s).
Per semplicità di notazioni, scriviamo
xu invece di
xu(u(t,s),v(t,s)) (e analoga notazione
per le derivate di y
e di z, e per le
derivate rispetto a v).
Si ha:
|
r→t(t,s) =[xua + xvb]i→ + [yua + yvb]j→ + [zua + zvb]k→
r→s(t,s) =[xuc + xvd]i→ + [yuc + yvd]j→ + [zuc + zvd]k→
|
La componente lungo il versore k→
del prodotto vettoriale r→t(t,s) ∧r→s(t,s)
è
|
[(xuyuac + xvyvbd + xuyvad + xvyubc) − (yuxuac + yvxvbd + yuxvad + yvxubc)]
= (xuyv − xvyu)(ad − bc).
|
Proseguendo in modo analogo al calcolo delle altre componenti si trova:
Teorema 202 Vale:
r→t(u(t,s),v(t,s))∧r→s(u(t,s),v(t,s)) = (ad−bc)r→u(u(t,s),v(t,s))∧r→v(u(t,s),v(t,s)).
Il numero ab − bc
è lo jacobiano del cambiamento di parametro. Esso è positivo per la definizione di
cambiamento di parametro.
Teorema 203 effettuando un cambiamento di parametro la normale alla
superficie non cambia né direzione né verso.
Per questa ragione si dice che i cambiamenti di parametro (che hanno jacobiano
positivo) lasciano invariata l’orientazione della superficie. Si dice che cambiano
l’orientazione della superficie quelle trasformazioni che hanno jacobiano
negativo.
6.4 Appendici
6.4.1 Appendice: le formule di Frenet per curve nello spazio
Torniamo a considerare le curve nello spazio e completiamo le considerazioni
svolte al paragrafo 6.1.3. In quel paragrafo abbiamo definito la tangente
t→(s) e la normale
n→(s) ad una curva. Il piano
identificato dai vettori t→(s)
e n→(s), applicati
in r→(s),
si chiama il piano osculatore alla curva nel punto
r→(s). Notiamo
ora che t→(s) ⋅n→(s)
è identicamente zero e quindi ha derivata nulla. Dunque,
|
t→(s) ⋅n→′(s) = −t→′(s) ⋅n→(s) = −k(s).
| (6.17) |
Introduciamo ora il versore b→(s),
definito da
b→(s) = t→(s) ∧n→(s).
Il versore b→(s) è quindi
ortogonale a t→(s) e
n→(s) ed orientato in modo
tale che la terna (t→(s),n→(s),b→(s))
sia orientata positivamente. Si veda la figura 6.10 per un esempio. Il sistema di assi
cartesiano ortogonali che abbiamo descritto varia da punto a punto della curva.
Per questa ragione si chiama sistema di riferimento mobile sulla curva.
Il vettore b→(s)
si chiama il versore binormale alla curva. La derivata di
b→(s) è ortogonale
a b→(s) perché
||b→(s)|| = 1 per ogni
s e quindi appartiene
al piano di t→(s)
e n→(s) per
ogni s.
Si ha quindi
b→′(s) = α(s)t→(s) + β(s)k→(s).
D’altra parte,
b→′(s) = [t→′(s)] ∧n→(s) + [t→(s)] ∧n→′(s).
Ora, t→′(s) è
colineare con n→(s)
e quindi il loro prodotto vettoriale è nullo. Rimane quindi
b→′(s) = [t→(s)] ∧n→′(s).
Il vettore [t→(s)] ∧n→′(s) è
ortogonale sia a t→(s)
che a n→′(s). E’ quindi
un multiplo di n→(s).
Dunque, per ogni s
esiste un numero τ(s)
tale che
|
b→′(s) = −τ(s)n→(s).
| (6.18) |
Da qui si trova
τ(s) = −b→′(s) ⋅n→(s).
Essendo b→(s) ⋅n→(s)
identicamente zero, derivando si trova anche che
|
τ(s) = b→(s) ⋅n→′(s).
| (6.19) |
Il numero τ(s)
può essere positivo negativo o nullo. Esso si chiama la torsione della curva. Cerchiamo ora di
esprimere n→′(s)
mediante t→(s) e
b→(s). Ciò è possibile
perchè n→′(s), essendo
ortogonale a n→(s),
è nel piano di t→(s)
e di b→(s).
Dunque
|
n→′(s) = γ(s)t→(s) + δ(s)b→(s).
| (6.20) |
Moltiplicando scalarmente i due membri di (6.20) per
t→(s) ed
usando (6.17) si trova
γ(s) = −k(s).
Analogamente, moltiplicando scalarmente (6.20) per
b→(s) ed
usando (6.19) si trova
δ(s) = n→′(s) ⋅b→(s) = τ(s).
Si trova quindi che i versori t→(s),
n→(s),
b→(s)
verificano
t→′(s) =k(s)n→(s)
n→′(s) = − k(s)t→(s) + τ(s)b→(s)
b→′(s) = − τ(s)n→(s).
Si chiamano queste le equazioni di Frenet per curve di
ℝ3. Il sistema di riferimento
dato dai tre versori t→(s),
n→(s),
b→(s) applicati
in r→(s) si
chiama ancora il riferimento mobile sulla curva.
6.4.2 Appendice: Curve in ℝn
La maggior parte delle considerazioni che abbiamo svolto si estendono senza alcuna
diffcoltà a curve
γ : t →r→(t),r→ ∈ ℝn.
Per esempio è ancora vero che una curva in
ℝn che è semplice
è identificata dal suo sostegno a meno dell’orientazione; si definisce ancora la lunghezza
dell’arco γ
ponendo
Lγ = ∫
ab||r→̇(t)||dt;
è quindi possibile definire il parametro d’arco. La tangente e la
normale si definiscono ancora nel medesimo modo come per le curve in
ℝ3. Non
esiste invece una unica “binormale”. Per completare il il riferimento mobile
sulla curva si devono introdurre, oltre alla tangente ed alla normale, altri
n − 2
vettori e quindi le equazioni di Frenet diventano più complesse.
Capitolo 7
Integrazione delle funzioni di più variabili
In questo capitolo introdurremo gli integrali di funzioni di due o tre variabili. Le idee
che si seguono per definire l’integrale sono simili a quelle che si usano per definire
l’integrale delle funzioni di una sola variabile e quindi le illustreremo per sommi
capi.
Una differenza importante tra le definizione di integrali per le funzioni di una o più
variabili è nella scelta dei domini di integrazione. Per le funzioni di una
variabile è naturale scegliere gli intervalli. Per le funzioni di più variabili
c’è molta più libertà. Noi sceglieremo come domini di integrazione gli
insiemi che sono delimitati da grafici di funzioni continue (si veda più avanti
per una definizione più precisa). Tali insiemi si chiameranno domini di
integrazione. Studieremo la definizione dell’integrale di di una classe di funzioni
che saranno costruite a partire da funzioni continue su insiemi chiusi e
limitati.
Dovremo usare la seguente proprietà delle funzioni che sono
continue su un qualsiasi insieme insieme chiuso e limitato
𝒟:
per ogni
𝜖 > 0
esiste
δ > 0
con questa proprietà:se
R
è un qualsiasi rettangolo contenuto in
𝒟
le cui diagonali hanno lunghezza minore di
δ
allora
0 ≤ max Rf − min Rf ≤ 𝜖.
La proprietà importante è che la posizione di
R in
𝒟 non
ha importanza. Inoltre, non abbiamo indicato esplicitamente le variabili
della funzione perché questo risultato vale per funzioni di un qualsiasi
numero di variabili (anche per funzioni di una sola variabile. In questo caso
R = [a,b],
nonostante che questo risultato non sia stato provato nel corso di Analisi
Matematica 1.) Questa proprietà delle funzioni continue su insiemi chiusi e
limitati si chiama continuità uniforme.
Introduciamo prima l’integrale di funzioni di due variabili, che presenteremo con
maggiori dettagli, e poi l’integrale delle funzioni di tre variabili, che presenteremo in
modo più conciso.
7.1 Integrazione delle funzioni di due variabili
Chiameremo dominio di integrazione semplice un insieme che ha una delle
proprietà seguenti:
- è trapezoide di una funzione y = g(x)
continua definita su un intervallo limitato e chiuso (dell’asse delle ascisse)
oppure x = g(y)
continua su un intervallo limitato e chiuso (dell’asse delle ordinate);
- oppure è differenza insiemistica di trapezoidi.
Va notato esplicitamente che ogni dominio di integrazione semplice
è limitato, per il Teorema di Weiestrass. Inoltre, assumiamo che il
dominio di integrazione semplice sia chiuso, ossia contenga
i punti della sua frontiera. Nel caso specifico di un dominio di
integrazione semplice compreso tra due grafici di funzioni della variabile
x ∈ [a,b],
includeremo nel dominio sia i due grafici che i due
segmenti che lo delimitano a destra (punti di ascissa
a)
ed a sinistra (punti di ascissa b).
Un insieme chiuso e limitato 𝒟
si chiama dominio di integrazione quando si può rappresentare come unione
di domini di integrazione semplici in modo tale che due qualsiasi di essi
non abbiano punti interni comuni (ossia, gli eventuali punti comuni a due
domini di integrazione semplici appartengono alle rette o ai grafici che li
delimitano).
Per brevità un dominio di integrazione semplice si chiamerà “dominio semplice”
ma è importante ricordare che è un caso speciale di dominio di integrazione. In
conclusione, un dominio di integrazione si rappresenta (non in modo unico) come
unione di domini semplici
|
𝒟 = D1 ∪ D2 ∪⋯ ∪ DnDi ∩ Dj privo di punti interni.
| (7.1) |
La figura 7.1 mostra esempi di domini di integrazione.
Quello a sinistra è la parte del trapezoide di una funzione
y = g(x)
x ∈ [a,b] che è sopra alla retta
orizzontale y = m ed automaticamente
sotto alla retta y = M = max g(x).
E’ quindi la differenza insiemistica tra il trapezoide di
g(x) e quello della funzione
che vale costantemente m.
Il dominio di integrazione a destra è più complesso, suddiviso mediante grafici di varie
funzioni y = y(x),
oppure x = x(y),
ciascuna continua e definita su un opportuno intervallo limitato e chiuso.
Osservazione 204 Si noti che:
- un dominio di integrazione è un insieme chiuso e limitato. Questo
implica che una funzione continua definita su un dominio di integrazione
è limitata.
- Come abuso di linguaggio, se Ω
è un dominio di integrazione, talvolta chiameremo dominio di integrazione
l’insieme dei suoi punti interni; ossia l’insieme Ω
privato delle curve che lo delimitano. Anche in questo caso, le funzioni
continue che integreremo dovranno avere estenzione continua alla frontiera
dell’insieme.
- uno stesso dominio di integrazione può rappresentarsi in più modi
come unione di insiemi semplici: per esempio il trapezoide della funzione
sin x,
0 ≤ x ≤ π
è un dominio di integrazione semplice che può rappresentarsi anche
come 𝒟1 ∪𝒟2
con 𝒟1
il trapezoide di sin x,
0 ≤ x ≤ π∕2
e 𝒟2
quello di sin x,
π∕2 ≤ x ≤ π.
- Si potrebbe provare che la chiusura di una regione di Jordan delimitata
da una curva regolare è un dominio di integrazione; e quindi anche
l’insieme ottenuto togliendogli la regione delimitata da una seconda curva
di Jordan regolare lo è. _
Introduciamo ora la classe di funzioni per cui definiremo
l’integrale. Chiamiamo
integrabile una funzione f(x,y) definita
su un dominio di integrazione 𝒟
(o almeno nei suoi punti interni) e con questa proprietà: E’ possibile trovare una rappresentazione di
𝒟 come in (7.1) in modo
tale che per ogni indice i
la funzione f|D
i(x,y)
ammetta estensione continua al dominio semplice
Di.
Ossia, gli eventuali punti di discontinuità della funzione
f(x,y) devono
essere sulle rette o grafici che delimitano i domini semplici che compongono
𝒟
.
7.1.1 La definizione di integrale
Sia f(x,y) una funzione
integrabile. Per definirne l’integrale, procediamo in questo modo: definiamo l’integrale di
f(x,y) su ciascuna dei domini
semplici Di e quindi definiamo
l’integrale su 𝒟 come somma
degli integrali sui domini Di.
Si noti che il dominio 𝒟
si potrà decomporre in più modi e quindi andrebbe provato che l’integrale di
f(x,y) non
dipende dalla decomposizione scelta per il dominio. Questo è vero ma noi non lo
proveremo. Per semplicità limitiamoci a illustrare la definizione dell’integrale di
f(x,y) sul
dominio semplice rappresentato nella figura 7.1 a sinistra. Indichiamo con
T tale
dominio semplice,
T = {(x,y),0 ≤ a ≤ b,m ≤ g(x) ≤ M}
Si segua il procedimento guardando la figura 7.2.
Dividiamo [a,b]
in N parti uguali
con i punti a0 = a,
ak = kb−a
N .
Consideriamo quindi i segmenti verticali i cui punti hanno ascissa
ak e che sono
contenuti in T,
come in fig. 7.2, a sinistra. Suddividiamo ora anche il segmento
[m,M] dell’asse delle
ordinate in L tratti
uguali. Le rette orizzontali i cui punti hanno ordinata uguale ai punti di suddivisione dell’intervallo
[m,M] disegnano una divisione
dell’insieme T in rettangoli
completamente contenuti in T,
e inoltre certi sottoinsiemi a lati non rettilinei, che escludiamo.
Si guardi la figura 7.2, a destra. In questo modo il trapezoide
della funzione viene ad essere approssimato da una rete di al più
NL rettangolini, che
indichiamo con Ri,j,
0 ≤ i ≤ N − 1,
0 ≤ j ≤ L − 1. Ciascuno di questi
rettangoli ha area b−a
N M−m
L .
Indichiamo con U−
la loro unione. Notiamo che nessuno dei rettangolini è a cavallo del grafico di
g(x) e che
U− ⊆ T. Per ipotesi,
la funzione f(x,y)
appartiene alla classe delle funzioni integrabili e quindi la sua restrizione a
T
ammette estensione continua a tutti i punti del dominio di integrazione
T, che è chiuso e limitato.
Indichiamo ancora con f(x,y)
tale estensione, che è uniformemente continua. Costruiamo ora le somme
|
sN,L = ∑
i,j min (x,y)∈Ri,jf(x,y) ⋅M − m
L ⋅b − a
N
SN,L = ∑
i,j max (x,y)∈Ri,jf(x,y) ⋅M − m
L ⋅b − a
N
|
Queste somme sono estese a tutti i rettangoli che appartengono ad
U−. Ora usiamo l’uniforme
continuità di f(x,y). Si
fissi un qualsiasi 𝜖 > 0 e
il corrispondente δ > 0.
Se N ed
L sono abbastanza
grandi, diciamo N ≥ N0,
L ≥ L0,
la diagonale di ciascuno dei rettangoli costruiti misura meno di
δ e quindi
per N ≥ N0,
L ≥ L0 si
ha
0 ≤ [max Ri,jf(x,y) − min Ri,jf(x,y)] < 𝜖.
In particolare
0 ≤ SN0,L0 − sN0,L0 ≤somma delle aree dei rettangoli 𝜖 ≤(b − a)(M − m) 𝜖.
Ma,
|
0 ≤ inf{SN,L}− sup{sN,L}≤ SN0,L0 − sN0,L0 ≤
≤somma delle aree dei rettangoli 𝜖 ≤(b − a)(M − m) 𝜖.
|
Dunque
inf{SN,L} = sup{sN,L}
e questo numero si chiama l’integrale di
f(x,y) sul
trapezoide T.
Esso si indica col simbolo
∫
T f(x,y)dxdy.
In modo analogo si definisce l’integrale su ogno altro dominio
Di. Si
definisce quindi
|
∫
𝒟f(x,y)dxdy = ∑
i ∫
Dif(x,y)dxdy.
| (7.2) |
Osservazione 205 E’ ovvio dalla costruzione che abbiamo fatto che se
f(x,y) ≥ 0 allora
il suo integrale si interpreta come il volume del solido compreso tra l’insieme
𝒟 del
piano z = 0
ed il grafico della funzione. Se in particolare si sceglie
f(x,y) identicamente
uguale ad 1,
si trova una numero che ha senso interpretare come area del dominio di
integrazione. Ossia per definizione:
|
area di 𝒟 = ∫
𝒟1dxdy.
| (7.3) |
Se accade che 𝒟
è grafico di una funzione y = g(x) ≥ 0
continua su [a,b]
abbiamo due diverse definizioni di area: quella appena scritta e quella data
durante il corso di Analisi Matematica 1: area del trapezoide di una funzione
positiva uguale (per definizione!) al suo integrale. Si tratta di due definizioni
diverse ma vedremo che conducono al medesimo numero. Un fatto da sottolineare
è questo: ∫
abg(x)dx
è l’area del trapezoide solo se g(x) ≥ 0.
Invece, la (7.3) dà il valore dell’area anche quando 𝒟
è trapezoide di una funzione che cambia segno. _
Talvolta, un integrale di una funzione di due variabili si chiama anche integrale doppio
Per contrasto, l’integrale di una funzione di una sola variabile,
∫
abf(x)dx
si chiama anche integrale semplice
7.1.2 Le proprietà dell’integrale
Le proprietà dell’integrale sono le stesse come nel caso degli integrali semplici:
- la linearità: se α
e β
sono numeri e f(x,y),
g(x,y)
sono funzioni continue sullo stesso dominio di integrazione 𝒟,
vale
∫
𝒟αf(x,y) + βg(x,y) dxdy = α∫
𝒟f(x,y)dxdy + β∫
𝒟g(x,y)dxdy;
- additività: se il dominio di integrazione 𝒟
è unione di due,
𝒟 = 𝒟1 ∪𝒟2
e se la funzione f(x,y)
è integrabile sia su 𝒟1
che su 𝒟2,
allora è anche integrabile su 𝒟,
e viceversa; e inoltre
∫
𝒟f(x,y)dxdy = ∫
𝒟1f(x,y)dxdy + ∫
𝒟2f(x,y)dxdy.
- monotonia: f(x,y) ≤ g(x,y)
per ogni (x,y) ∈𝒟
implica
∫
𝒟f(x,y)dxdy ≤∫
𝒟g(x,y)dxdy.
- Dalla monotonia si deduce
∫
𝒟f(x,y)dxdy ≤∫
𝒟|f(x,y)|dxdy.
Anche il teorema della media si può riformulare. Indichiamo con
A(𝒟) l’area
di 𝒟,
calcolata sommando le aree delle singole regioni che la compongono. Vale:
A(𝒟) ⋅min (x,y)∈𝒟f(x,y) ≤∫
𝒟f(x,y)dxdy ≤ A(𝒟) ⋅max (x,y)∈𝒟f(x,y) .
Ne segue:
Teorema 206 Se
𝒟𝜖
è una circonferenza di raggio
𝜖
e centro fissato vale
lim 𝜖→0 ∫
𝒟𝜖f(x,y)dxdy = 0.
7.1.3 Domini di integrazione definiti mediante curve di Jordan
Sia
γ : t → x(t)i→ + y(t)j→
una curva di Jordan regolare. Applicando il Teorema della funzione implicita si
vede che il sostegno è localmente un grafico e si potrebbe provare che il sostegno
è grafico di un numero finito di funzioni. Dunque, l’unione della regione
Ωγ, interna alla
curva γ e del
suo sostegno è un dominio di integrazione. Come si è notato all’osservazione 204, diremo
che la regione Ωγ
stessa è un dominio di integrazione e quindi è possibile:
- integrare una funzione su una regione di Jordan, se la funzione è
continua sulla chiusura della regione;
- assegnare un’area ad una regione di Jordan (ciò che si fa integrando la
funzione identicamente uguale ad 1);
- approssimare l’area di una regione di Jordan mediante la somma delle
aree di un numero finito di rettangoli con lati paralleli agli assi coordinati.
Con lo stesso abuso di linguaggio illustrato all’osservazione 204, diremo ancora che una
regione di Jordan si può approssimare mediante rettangoli.
7.1.4 Riduzione di integrali doppi ad integrali iterati
Torniamo a considerare le somme sN,L
ed SN,L
che servono per definire l’integrale doppio. Consideriamo per esempio le
sN,L:
sN,L = ∑
i,j min (x,y)∈Ri,jf(x,y) ⋅M − m
L ⋅b − a
N .
Calcoliamo le somme prima di tutto sommando i termini che corrispondono a
rettangolini che appartengono alla stessa striscia verticale, ossia scrivendo
|
sN,L = ∑
i,j min (x,y)∈Ri,jf(x,y) ⋅M − m
L ⋅b − a
N
= ∑
i ∑
j min (x,y)∈Ri,jf(x,y) ⋅M − m
L ⋅b − a
N .
|
fissiamo un punto xi in
ciascuno degli intervalli [ai,ai+1).
Si mostra che per L → +∞
tende a zero la differenza tra la parentesi graffa e l’integrale
∫
0g(xi)f(x
i,y)dy
ove xi è un qualsiasi
punto dell’intervallo [ai,ai+1);
e quindi che
|
sN,L = ∑
i,j min (x,y)∈Ri,jf(x,y) ⋅M − m
L ⋅b − a
N
= ∑
ib − a
N ∫
0g(xi)f(x
i,y)dy + 𝜖(L,N)
|
con
lim 𝜖(L,N) = 0;
Ma, per N → +∞,
le somme
∑
i=0N−1b − a
N ∫
0g(xi)f(x
i,y)dy
convergono all’integrale della funzione di
x
∫
0g(x)f(x,y)dy,
ossia all’integrale iterato di f(x,y).
Dunque, per calcolare ∫
𝒟f(x,y)dxdy
si può procedere come segue:
- Si proietta ortogonalmente 𝒟
sull’asse delle ascisse, ottenendo un intervallo [a,b];
- Si traccia la retta parallela all’asse delle ordinate e che passa da x ∈ [a,b].
Si indica con 𝒮x
l’intersezione di tale retta con 𝒟.
L’insieme 𝒮x
è unione di un numero finito di intervalli.
- Si ha: ∫
𝒟f(x,y)dxdy = ∫
ab ∫
𝒮xf(x,y)dydx.
Si veda la figura 7.3
Naturalmente la stessa procedura vale anche scambiando il ruolo dell’asse delle ascisse
con quello dell’asse delle ordinate. Consideriamo un caso particolare: supponiamo che
𝒟 sia il trapezoide
della funzione k(x),
x ∈ [a,b],
e che la funzione integranda sia identicamente uguale ad
1. Sia
inoltre k(x)
non negativa. In tal caso,
∫
𝒟1dxdy = ∫
ab ∫
0k(x)1dydx = ∫
abk(x)dx
in accordo con quanto detto nell’osservazione 205. Il metodo visto “riduce” il
calcolo di un integrale doppio a quello di un integrale iterato, e quindi a
quello di due integrali semplici. Però esso può anche usarsi al contrario,
per ricondurre il calcolo di un integrale iterato calcolato prima rispetto ad
x e poi rispetto
ad y al calcolo
di un integrale doppio; e quindi al calcolo di un integrale iterato calcolato prima rispetto
ad y e poi
rispetto ad x.
Quando si opera in questo modo su un integrale iterato si dice che si
scambia l’ ordine d’integrazione.
7.2 Integrazione delle funzioni di tre variabili
L’integrazione delle funzioni di tre variabili si introduce in modo del tutto analogo a
quella relativa a funzioni di due variabili. Prima di tutto si scelgono i domini di
integrazione semplici: questi sono i solidi delimitati dai grafici di due funzioni, per
esempio
ϕ(x,y) ≤ z ≤ ψ(x,y)
con (x,y) ∈𝒟,
dove 𝒟
è un dominio di integrazione semplice per funzioni di due variabili. Anche i
domini di integrazioni semplici per funzioni di tre variabili sono insiemi chiusi.
Come dominio di integrazione per funzioni di tre variabili intendiamo l’unione di un
numero finito di tali domini semplici, purché l’intersezione tra due qualsiasi di essi
non contenga punti interni. Definiamo ora l’insieme delle funzioni integrabili. Una
funzione definita su un dominio di integrazione si dice integrabile quando la sua
restizione all’interno di ciascuno dei domini semplici ammette estensione continua
al dominio semplice stesso. Ciò detto è facile dividere un dominio di
integrazione in “piccoli” parallelepipedi e costruire le analoghe delle somme
sN ed
SN e
quindi definire
∫
𝒟f(x,y,z)dxdydz
come estremo comune ai due insiemi {sN,L,K}
ed {SN,L,K} che ora verranno a
dipendere da tre indici N,
L,
K. Si
ottiene cosìun integrale che si chiama anche integrale triplo
Osservazione 207 Per definizione, il volume di un dominio di integrazione
𝒟⊆ ℝ3
è
∫
𝒟1dxdydz.
Le proprietà elencate al paragrafo 7.1.2 per gli integrali doppi valgono anche per gli
integrali tripli. Per gli integrali tripli, il Teorema 210 si riformula come segue:
Teorema 208 Sia (u,v,w)↦ x(u,v,w),y(u,v,w),z(u,v,w)
una trasformazione continua da un dominio di integrazione 𝒟1
ad un dominio di integrazione 𝒟.
Supponiamo che la trasformazione ammetta derivate parziali continue nei punti
interni di 𝒟1
e che le derivate abbiano estensione continua alla frontiera, e che il suo determinante
jacobiano J(u,v,w)
non si annulli. Per ogni funzione f(x,y,z)
continua su 𝒟
si ha:
∫
𝒟f(x,y,z)dxdydz = ∫
𝒟1f x(u,v,w),y(u,v,w),z(u,v,w) J(u,v,w)dudvdw.
Invece, il metodo di riduzione va esaminato esplicitamente.
7.3 Formula di riduzione per gli integrali tripli
Il calcolo degli integrali tripli si può ricondurre al calcolo di integrali iterati.
Illustriamo il metodo nel caso particolare in cui il dominio di integrazione
𝒟 è
compreso tra due grafici
𝒟 = {(x,y,z)|ϕ(x,y) ≤ z ≤ ψ(x,y)}.
Indichiamo con
𝒟z = {(x,y)|∃w per cui (x,y,w) ∈𝒟}
ossia la proiezione ortogonale di 𝒟
sul piano z = 0.
Dunque:
- se (x,y)∉𝒟z
allora la retta verticale per (x,y)
non interseca 𝒟;
- se (x,y) ∈𝒟z
allora la retta verticale per (x,y)
interseca 𝒟
nel segmento verticale di estremi (x,y,ϕ(x,y))
e (x,y,ψ(x,y)).
Si noti che questo segmento potrebbe essere ridotto ad un punto.
Vale:
∫
𝒟f(x,y,z)dxdydz = ∫
𝒟z ∫
ϕ(x,y)ψ(x,y)f(x,y,z)dzdxdy.
In questo modo il calcolo dell’integrale triplo si è ricondotto al
calcolo di un integrale semplice, seguito da quello di un integrale
doppio.
Si veda la figura 7.4, a sinistra.
Si può anche procedere in modo diverso: supponiamo di sapere che
𝒟z sia
delimitato da due grafici, per esempio
𝒟z = {(x,y)|h(y) ≤ x ≤ k(y)}
e sia [a,b] il dominio
comune ad h(y)
e k(y).
Allora vale:
∫
𝒟f(x,y,z)dxdydz = ∫
ab ∫
𝒟̃yf(x,y,z)dxdzdy
dove 𝒟̃y è l’intersezione
di 𝒟 col piano
parallelo agli assi x e
z, passante per il punto
(0,y, 0).
Si veda la figura 7.4, a destra.
7.3.1 Integrazione e Cambiamento di variabili
Nel caso degli integrali semplici, sotto opportune ipotesi si prova la formula
∫
abf(x)dx = ∫
ϕ−1(a)ϕ−1(b)f(ϕ(t))ϕ′(t)dt.
Si noti però che ϕ−1(a) può
anche essere maggiore di ϕ−1(b),
ciò che è lecito perché nel caso degli integrali semplici abbiamo
definito l’integrale orientato. D’altra parte, questa formula non si prova
usando direttamente le proprietà dell’integrale. Piuttosto si prova che
questa formula vale per il calcolo delle primitive, e quindi anche per il
calcolo dell’integrale grazie al teorema fondamentale del calcolo integrale.
Mostriamo come a questa formula, sotto opportune ipotesi, si possa
anche giungere direttamente dalla definizione di integrale semplice. Sia
f(x) una funzione continua
definita su in intervallo [a,b]
e sia x = ϕ(t)
una funzione monotona strettamente crescente da un intervallo
[α,β] su
[a,b], che
è anche derivabile. Bisogna ricordare questi fatti:
Quando la finezza della partizione tende a zero, le somme (7.4) tendono all’integrale
∫
abf(x)dx.
Essendo la funzione ϕ
monotona e suriettiva, ogni ai
proviene da un unico αi,
ai = ϕ(αi).
Dunque la somma (7.4) è anche uguale a
∑
i=1nf(ξ
i)[ϕ(αi+1) − ϕ(αi)].
Questa non è una somma di quelle che conducono alla definizione di un integrale,
ma ad essa facilmente si riconduce. Infatti, dal Teorema di Lagrange, esiste un punto
ci tale
che
[ϕ(αi+1) − ϕ(αi)] = ϕ′(c
i)(αi+1 − αi).
Ricordando che i numeri ξi
si possono scegliere in modo arbitrario, scegliamo
ξi = ϕ(ci). La
monotonia di ϕ
mostra che ci ∈ (αi,αi+1).
In questo modo la (7.4) diviene
|
∑
i=1nf(ϕ(c
i))ϕ′(c
i)[αi+1 − αi].
| (7.5) |
La finezza della partizione di [a,b]
tende a zero se e solo se tende a zero la finezza della partizione di
[α,β]. Quando
la finezza della partizione tende a zero, le somme (7.4) tendono all’integrale di
f(x), quelle di (7.5)
tendono all’integrale di f(ϕ(t))ϕ′(t).
D’altra parte le due somme hanno lo stesso valore e quindi si trova
∫
abf(x)dx = ∫
αβf(ϕ(t))ϕ′(t)dt.
Osservazione 209 Notiamo esplicitamente:
- in questo calcolo la crescenza di ϕ
si è usata: è αi < αi+1
proprio perchè ϕ
è crescente. Se invece ϕ
decresce, sarà β < α
e in (7.5) si ha αi+1 < αi
e quindi al limite si trova
∫
abf(x)dx = ∫
αβf(ϕ(t))ϕ′(t)dt.
Ma ora β < α
e quindi riordinando l’ordine degli estremi di integrazione si trova
|
∫
abf(x)dx = −∫
βαf(ϕ(t))ϕ′(t)dt
= ∫
βαf(ϕ(t))[−ϕ′(t)]dt = ∫
βαf(ϕ(t))|ϕ′(t)|dt.
|
- il ruolo del numero ϕ′(c):
è il coeffciente che trasforma la lunghezza di
[αi,αi+1] nella lunghezza
di [ai,ai+1]. Si noti che se
ϕ′ non si annulla su
[a,b] (estremi inclusi)
esistono numeri m,
M
tali che
m|αi − αi+1|≤|ai − ai+1|≤ M|αi − αi+1|.
- Nel caso degli integrali semplici, la formula vale anche senza richiedere la monotonia di
ϕ perchè,
intuitivamente, se per t
che percorre [α,β] il
punto ϕ(t) percorre più
volte un intervallo [x′,x″] ⊆ [a,b],
deve percorrerlo un numero dispari di volte, in versi opposti; e grazie
all’esistenza dell’integrale orientato, i contributi dei passaggi
2 e
3 si elidono, lo stesso
per i passaggi 4
e 5
ecc. Un fenomeno analogo non potrà aversi per funzioni
di più variabili e quindi in tal caso dovremo imporre a
ϕ
di essere biunivoca. _
Vediamo ora quali problemi si incontrano nel cercare di estendere il ragionamento
appena fatto a funzioni di più variabili. In questo caso dovremo avere
f(x,y) definita su un dominio di
integrazione 𝒟 e dovremo avere
una trasformazione (x,y) = Φ(u,v) = (ϕ1(u,v),ϕ2(u,v)) da un
dominio di integrazione 𝒟′ nel
dominio di integrazione 𝒯.
La Φ dovrà essere
biunivoca da 𝒟′
su 𝒟 e
differenziabile (un’ulteriore condizione si dirà in seguito). L’integrale di
f(x,y) si definisce suddividendo
𝒟 in tanti piccoli
rettangoli, diciamo Ri.
Un rettangolo Ri è
immagine mediante Φ
di un sottoinsieme Ri′
di 𝒟′ che però non è
un rettangolo. Se la Φ
è lineare R′
è un parallelogramma, altrimenti è una figura più complessa. Ciò nonostante,
si potrà tentare di ripetere gli argomenti visti sopra se:
- si potrà trovare una relazione tra l’area di Ri
e quella di Ri′;
- l’area dei rettangoli Ri
tende a zero se e solo se l’area degli insiemi Ri′
tende a zero.
La relazione tra l’area di Ri e
quella di Ri′è nota nel caso
in cui la trasformazione Φ
sia lineare: è
(area di Ri) = | det Φ|(area di Ri′).
Qui Φ indica la matrice
della trasformazione Φ,
calcolata rispetto a coordinate ortogonali. Nel caso non lineare una formula analoga
alla precedente ancora vale, con un errore che è di ordine superiore rispetto all’area di
R′, quando
questa tende a zero. Questo risponde alla prima questione. La seconda richiesta, l’area degli
Ri tende a zero se e solo se
l’area degli Ri′ tende a zero,
è soddisfatta quando det Φ≠0 su
𝒟′. Con queste informazioni,
nel caso in cui Φ
sia una trasformazione lineare è relativamente facile provare il risultato seguente,
mimando la dimostrazione vista sopra per il caso di funzioni di una variabile. Nel caso
in cui Φ
sia non lineare, il risultato seguente vale ancora ma la dimostrazione è piuttosto
complessa:
Teorema 210 Siano
𝒟
e
𝒟′
due domini di integrazione. Sia
(x,y) = Φ(u,v) = (ϕ1(u,v),ϕ2(u,v))
una trasformazione invertibile da 𝒟′
su 𝒟.
Supponiamo che questa trasformazione sia di classe C1
su una regione Ω
che contiene 𝒟′.
Sia det J(u,v)
lo jacobiano della trasformazione. Supponiamo che det J(u,v)
non si annulli su 𝒟′.
Sotto queste condizioni vale:
∫
𝒟f(x,y)dxdy = ∫
𝒟′f(ϕ1(u,v),ϕ2(u,v)) ⋅| det J(u,v)|dudv.
Come abbiamo detto, questo teorema estende il teorema di cambiamento di variabili
negli integrali semplici. Nell’uso però esso ha un ruolo diverso. Nel caso
degli integrali semplici il metodo di cambiamento di variabili si usa per
trasformare la funzione in una di cui sia più facile trovare la primitiva. Nel caso
degli integrali doppi si usa la trasformazione di variabili per passare da
un dominio più complicato ad uno più semplice. Per esempio, si voglia
calcolare
∫
𝒟x2 + y2dxdy
con 𝒟 la
circonferanza x2 + y2 ≤ 1.
Esprimendo x ed
y mediante le
coordinate polari ρ
e 𝜃, si
trova
x = ρ cos 𝜃,y = ρ sin 𝜃,0 ≤ ρ ≤ 1,0 ≤ 𝜃 ≤ 2π.
Notando che lo jacobiano della trasformazione è semplicemente
ρ, il
calcolo richiesto si riduce a quello dell’integrale iterato
∫
02π ∫
01ρ2dρd𝜃 = 2
3π.
Osservazione 211 Si noti che lo jacobiano della trasformazione a coordinate
polari si annulla nell’origine e quindi il Teorema 210 a rigore non
può applicarsi. Si applichi però il teorema ad una corona circolare
𝜖 ≤ ρ ≤ 1
e poi si mandi
𝜖
a zero. Il Teorema 206 mostra che il contributo della circonferenza di raggio
𝜖
tende a zero e ciò giustifica l’uso delle coordinate polari per il calcolo
precedente. _
7.4 Alcuni jacobiani che è importante ricordare
Le trasformazioni di coordinate che si usano più comunemente sono le
trasformazioni a coordinate polari o ellittiche nel piano, a coordinate cilindriche o
sferiche nello spazio. Si ha:
̲ ̲ ̲ | coordinate | trasformazione | jacobiano
̲ ̲ ̲ |
| | Nel piano |
̲ ̲ ̲ |
| polari (ρ,𝜃) | x = ρ cos 𝜃 y = ρ sin 𝜃 | ρ
̲ ̲ ̲ |
| ellittiche (ρ,𝜃) | x = aρ cos 𝜃 y = bρ sin 𝜃 | abρ
̲ ̲ ̲ |
| | Nello spazio |
̲ ̲ ̲ |
| cilindriche (ρ,𝜃,z) | x = ρ cos 𝜃
y = ρ sin 𝜃 z = z | ρ
̲ ̲ ̲ |
| sferiche (ρ,𝜃,ϕ) | x = ρ cos 𝜃 sin ϕ
y = ρ sin 𝜃 sin ϕ
z = ρ cos ϕ | ρ2 sin ϕ
̲ ̲ ̲ |
|
Si noti che nella formula di cambiamento di coordinate per gli integrali multipli compare il
valore assoluto dello jacobiano, mentre la tavola precedente riporta lo jacobiano per
sottolineare che i sistemi di coordinate che abbiamo introdotto, con le coordinate che
si susseguono nell’ordine indicato nella definizione delle coordinate, hanno jacobiano
positivo. Dunque la matrice jacobiana di tali trasformazioni non altera l’orientazione di
ℝ3.
7.4.1 Volumi delimitati da superfici di rotazione
Consideriamo il grafico di una funzione sul piano
(y,z), descritto
dall’equazione z = f(y).
Per fissare le idee, supponiamo che la funzione sia definita (e continua) su
[0,Y ] e che
prenda valori positivi. Facendo ruotare i punti del grafico intorno all’asse
z, si
trova la superficie descritta dall’equazione
z = f x2 + y2 .
Si vuol calcolare il volume dell’insieme
V = (x,y,z)|0 ≤ z ≤ f x2 + y2 ;
ossia il volume dell’insieme compreso tra il piano
z = 0 e la
superficie. Vogliamo quindi calcolare
∫
V dxdydz.
Passiamo a coordinate cilindriche
x =r cos 𝜃 y = r sin 𝜃
z =z.
Si calcola facilmente che lo jacobiano della trasformazione è
r.
Dunque va calcolato
∫
ℛrdrdzd𝜃.
L’insieme ℛ
è ora
ℛ = (r,𝜃,z)|0 ≤ 𝜃 ≤ 2π, 0 ≤ r ≤ Y , 0 ≤ z ≤ f(r) .
Dunque, riducendo l’integrale triplo ad integrali iterati si trova |
V = ∫
02π ∫
0Y ∫
0f(r)1 ⋅ rdzdrd𝜃 = 2π∫
0Y rf(r)dr.
| (7.6) |
Supponiamo invece che il grafico che si fa ruotare sia dato mediante una funzione
y = f(z),
0 ≤ z ≤ Z.
Passando a coordinate cilindriche
x =r cos 𝜃 y = r sin 𝜃
z =z,
si deve integrare ora sull’insieme
ℛ̃ = (r,𝜃,z)|0 ≤ 𝜃 ≤ 2π,0 ≤ z ≤ Z,0 ≤ r ≤ f(z) .
Dunque, |
V = ∫
V 1dxdydz = ∫
02π ∫
0z ∫
0f(z)1 ⋅ rdrdzd𝜃 = π∫
0Zf2(z)dz.
| (7.7) |
Questa formula si chiama Formula di Guldino L’interpretazione geometrica di
queste formule si capisce facilmente approssimando gli integrali semplici mediante le
somme di Riemann, che conducono alla definizione stessa degli integrali. Consideriamo
prima di tutto l’integrale (7.6). Consideriamo una partizione dell’intervallo
[0,Y ] mediante i
punti yi.
Le somme di Riemann inferiori hanno forma
2π ∑
rif(ri)(yi+1 − yi)
ove ri è un punto di
minimo della funzione rf(r)
nell’intervallo [yi+1,yi].
Il punto (0,ri, 0)
dell’assse delle ordinate ruota, per descrivere la superficie, sulla circonferenza di raggio
ri.
Dunque, 2πri(yi+1 − yi)
è circa l’area della corona circolare descritta, durante la rotazione, dal segmento
[yi+1,yi].
Dunque, 2πri(yi+1 − yi)f(ri)
è (circa) il volume del più alto “guscio cilindrico” che insiste su tale
corona circolare, e che è sotto al grafico della funzione. Invece, le somme
di Riemann dell’integrale (7.7) si ottengono dividendo il segmento
[0,Z] con i
punti zi.
Le somme di Riemann sono
π ∑
f2(z̃
i)(zi+1 − zi) ,z̃i ∈ [zi,zi+1].
Ciascun addendo πf2(z̃
i)(zi+1 − zi)
rappresenta circa il volume di un cilindretto di raggio
f(z̃i) e base sul
segmento [zi+1,zi]:
in questo caso il volume si approssima come somma dei volumi di tali cilindretti. La
figura 7.5 illustra a sinistra il primo ed a destra il secondo caso (il volume da calcolare
è quello del solido compreso tra la parte di paraboloide disegnata ed il piano
z = 0).
7.5 Appendici
7.5.1 Appendice: Integrali impropri
Nel caso degli integrali di una variabile, è stato naturale definire
∫
0+∞f(x)dx = lim
R→+∞∫
0Rf(x)dx.
Una definizione analoga nel caso di integrali doppi è è molto
più delicata. Per vedere la ragione, consideriamo una funzione
f(x,y) definita su un
insieme illimitato I,
che interseca ogni disco
DR = {(x,y)|x2 + y2 ≤ R2}
in un dominio di integrazione. Allora, si può definire
∫
If(x,y)dxdy = lim R→+∞∫
I∩DRf(x,y)dxdy.
Però questa definizione privilegia i dischi. Niente garantisce che si giunga al
medesimo limite se, invece di dischi, si considerano i quadrati
QR = {(x,y)||x|≤ R,|y|≤ R}.
L’esempio seguente mostra che in generale usando dischi od usando quadrati si
trovano comportamenti diversi.
Esempio 212 L’insieme
I
è il primo quadrante e la funzione che si considera è
f(x,y) = sin x2 + y2 .
L’integrale si
DR
si calcola immediatamente passando a coordinate polari:
∫
DRf(x,y)dxdy = π
4 1 − cos R2 ,
privo di limite per R → +∞.
L’integrale su QR
si calcola in coordinate cartesiane: |
∫
QRf(x,y)dxdy = ∫
QR(sin x2 cos y2 + cos x2 sin y2)dxdy
= ∫
0R sin x2dx ∫
0R cos y2dy + ∫
0R cos x2dx ∫
0R sin y2dy.
|
Questi integrali non possono calcolarsi in modo esplicito, ma è possibile provare che il
limite per R → +∞
è finito. Infatti, si consideri per esempio
∫
0R cos x2dx = ∫
01 cos x2dx + ∫
1+∞ cos x2dx.
Integrando per parti, proviamo che è finito il
limite:
lim R→+∞∫
1R cos x2dx.
|
∫
1R cos x2dx = ∫
1R[2x cos x2] 1
2xdx = ∫
1R 1
2xd sin x2
= 1
2R sin R2 − sin 1 + ∫
1R 1
2x2 sin x2dx.
|
E ora,
lim R→+∞ 1
2R sin R2 = 0
mentre
lim R→+∞∫
1R 1
2x2 sin x2dx
esiste finito perché | 1
2x2 sin x2| < M∕x2
ed
∫
1+∞1∕x2dx = 1.
Si può però provare che se esiste finito |
lim R→+∞∫
DR|f(x,y)|dxdy
| (7.8) |
allora esiste finito
lim R→+∞∫
DRf(x,y)dxdy.
Sia inoltre 𝒟n
una successione di domini di integrazione con questa proprietà: esiste un disco di raggio
Rn contenuto
in 𝒟n, ed
Rn → +∞. Se
vale (7.8) allora
lim R→+∞∫
𝒟Rf(x,y)dxdy = lim R→+∞∫
DRf(x,y)dxdy.
Questo numero si chiama integrale improprio su
ℝ2
e la condizione (7.8) assicura che l’integrale improprio non
dipende dal modo con cui viene calcolato, usando gli insiemi
𝒟n con la proprietà
suddetta, che
𝒟n contiene un
disco di raggio Rn → +∞.
Considerazioni del tutto analoghe valgono anche nel caso in cui si consideri una funzione
f(x,y) definita su un dominio
di integrazione 𝒟,
ma tale che
lim (x,y)→(x0,y0)|f(x,y)| = +∞.
Sia D𝜖 un dico di
raggio 𝜖 > 0 e centro
(x0,y0) e supponiamo
che f(x,y) sia
integrabile su 𝒟− D𝜖.
Supponiamo che |
lim 𝜖→0 ∫
𝒟−D𝜖|f(x,y)|dxdy = L < +∞.
| (7.9) |
Allora esiste finito anche il limite seguente, che si chiama l’integrale improprio di
f(x,y) su
𝒟:
lim 𝜖→0 ∫
𝒟−D𝜖f(x,y)dxdy.
Anche in questo caso, la condizione (7.9) assicura che i dischi non hanno ruolo
privilegiato nella definizione dell’integrale.
Esempio 213 Sia
D
il disco di centro
(0, 0)
e raggio
1
e sia
f(x,y) = 1
x2 + y2 γ.
Vogliamo capire per quali valori di γ
la funzione f(x,y)
è integrabile su D.
Si deve quindi calcolare
∫
D−D𝜖 1
x2 + y2 γdxdy.
Passando a coordinate polari, è immediato calcolare che quest’integrale è
2π∫
𝜖1ρ 1
ργdρ.
Il limite per
𝜖 → 0
esiste finito se e solo se
1 − γ > −1ossia seγ < 2.
Si confronti col caso delle funzioni di una variabile:
∫
01 1
xγdx
esiste se e solo se γ < 1.
Considerazioni del tutto analoghe valgono per gli integrali tripli. In particolare, si
consideri l’analogo dell’esempio 213 e si provi che
∫
x2+y2+z2<1 1
x2 + y2 + z2 γdxdydz
esiste finito se e solo se γ < 3.
7.5.2 Appendice: Teorema dei valori intermedi e Teorema di Brower
Il Teorema dei valori intermedi per funzioni a valori reali e continue su
una regione connessa è stato provato al cap. 4, si veda il Teorema 130.
Mostriamo che la formula di cambiamento di variabili per gli integrali impropri
permette di provare un teorema dei valori intermedi anche per funzioni da
ℝ3 in
sé:
Teorema 214 (dei valori intermedi) Sia
ϕ(r→)
una funzione che trasforma la palla
B = {r→ = (x,y,z)|||r→||2 = x2 + y2 + z2 ≤ 1}
in se stessa e che inoltre
- è biunivoca;
- è di classe C1
- verifica ϕ(r→) = r→
nei punti della frontiera di B;
ossia nei punti tali che ||r→|| = 1.
Sotto queste ipotesi, la trasformazione ϕ(r→)
è suriettiva.
Dim. Per assurdo, supponiamo che esista un punto
r→0 che non appartiene all’immagine
di ϕ. Mostreremo in seguito
che esiste una sferetta
B1 di centro
r→0
nessuno dei cui punti appartiene all’immagine di
ϕ. Sia
𝜖 > 0 il raggio
di B1.
Sia f(r→) la
funzione cosìdefinita:
- f(r→) = 1
se r→ ∈ B,
||r→ −r→0|| < 𝜖∕2;
- f(r→) = 0
altrimenti.
La funzione f(r→)
non è continua ma è integrabile e
∫
Bf(x,y,z)dxdydz > 0.
Calcoliamo quest’integrale usando la formula di sostituzione di variabile:
L’integrale è anche uguale a
∫
Bf(ϕ(x,y,z))Jϕ(x,y,z)dxdydz.
Quest’integrale però è nullo, perché
ϕ(x,y,z)
prende valori solo nell’insieme in cui la funzione
f(x,y,z)
è nulla. Questa contraddizione prova che il punto
r→0 non
può esistere. Per completare la dimostrazione, mostriamo ora l’esistenza della palla
B𝜖. Proviamo che se la
palla B𝜖 non esiste allora
anche r→0 appartiene
all’immagine di ϕ.
Supponiamo quindi che ogni palla di centro
r→0 contenga punti
dell’immagine di ϕ. In tal
caso, esiste una successione {r→n}
di punti di B
tale che ϕ(r→n) →r→0.
Per il Teorema di Bolzano-Weierstrass, la successione
{r→n} ammette una
s.successione convergente: r→nk →r→̂
e
lim kϕ(r→nk) = ϕ(r→0).
Dunque, per continuità si ha
ϕ(r→̂) = ϕ(r→0).
Ciò completa la dimostrazione. _ Naturalmente, la dimostrazione
precedente può applicarsi al caso di funzioni definite su
ℝ2.
Osservazione 215 E’ possibile provare che il teorema precedente vale supponendo
solamente che la funzione ϕ(r→)
sia continua e verifichi ϕ(r→) = r→
se ||r→|| = 1,
senza richiedere né l’esistenza delle derivate né la biunivocità. _
Un corollario importante è il seguente:
Corollario 216 Non esiste una funzione
ϕ(r→) continua
in B e
tale che
- ϕ(r→) = r→
se ||r→|| = 1;
- ||ϕ(r→)|| = 1
per ogni r→ ∈ B.
Dim. Infatti, una tale funzione violerebbe il teorema dei valori intermedi. _ Il
teorema precedente ha una conseguenza importante, che va sotto il nome di
Teorema di punto fisso di Brower
Teorema 217 Sia
ψ(r→)
una funzione continua che trasforma la palla (chiusa)
B
in se stessa. Esiste un punto
r→0 ∈ B
tale che
ψ(r→0) = r→0.
Dim. Accenniamo alla dimostrazione. Supponiamo che tale punto non esista. Allora, per
ogni r→ ∈ B si ha
ψ(r→)≠r→. Consideriamo la
semiretta di estremo ψ(r→)
e che passa per r→.
Questa semiretta taglia la superficie della sfera in un punto che dipende da
r→. Associando ad
r→ tale punto, si
costruisce una funzione ϕ(r→)
che verifica |
|ϕ(r→)| = 1per ogni r→,
ϕ(r→) = r→se||r→|| = 1.
|
Inoltre, si potrebbe provare che la funzione
ϕ(r→) è continua.
Il Corollario 216 mostra che tale funzione non può esistere. Si noti che la funzione
ϕ(r→) non è biunivoca e
nemmeno di classe C1.
Però, abbiamo detto che il Teorema 214 vale con la sola ipotesi che la
ϕ(r→) sia
continua, si veda l’osservazione 215. E quindi questa è la sola ipotesi necessaria
per il Corollario 216. _
Capitolo 8
Integrali di curva e di superficie
Studiamo ora gli integrali definiti, invece che su intervalli o su parti di piano, su
curve e su superfici. Conviene premettere alcune considerazioni sui limiti di funzioni
definite su curve e, successivamente, su superfici.
In questa parte introdurremo certe notazioni e anche certi termini che non
sono affatto standardizzati. Riassumiamo alcuni termini nella tabella
seguente
Termine che uso io
Altri termini
integrale di curva di prima specie
ntegrale curvilineo; integrale curvilineo di prima specie.
integrale di curva di seconda specie
integrale di linea; integrale di linea di seconda specie.
integrale di superficie di prima specie
integrale superficiale.
integrale di superficie di seconda specie
integrale di superficie; integrale di flusso.
Il fatto da ricordare è questo: gli integrali di prima specie integrano
funzioni (a valori reali) definite su curve o su superfici; gli integrali
di seconda specie integrano campi vettoriali definiti su curve o su
superfici. N.B. Per ragioni tipografiche, alcune figure di questo capitolo si trovano
alla fine del capitolo stesso.
8.1 Funzioni definite su curve: la densità
Funzioni definite su curve, anche a valori vettoriali, si sono già incontrate:
abbiamo incontrato il campo vettoriale che ad ogni punto di una curva
associa la tangente oppure la normale alla curva nel punto stesso. Queste
funzioni possono intendersi come funzioni definite, per esempio, su
ℝ3,
con dominio il sostegno della curva. La definizione dei limiti per tali
funzioni presenta però una particolarità che va evidenziata. Sia
γ una
curva semplice e regolare, parametrizzata da
t →r→(t),t ∈ [a,b].
La curva è semplice. Dunque, ogni coppia di punti
r→0 e
r→1 di
γ
individua un arco
r→(t),s ∈ [t0,t1],
con t0
ed t1 gli
unici valori del parametro che verificano
r→0 = r→(t0),r→1 = r→(t1).
Introduciamo la notazione γr→0,r→1 per
indicare quest’arco e la notazione Lγ(r→0,r→1)
per indicarne la lunghezza (si veda il paragrafo (6.1.2):
Lγ(r→0,r→1) = ∫
t0t1
|r→′(ν)|dν.
Sia f(r→)
una funzione definita nei punti del sostegno di
γ. Chiamiamo densità
della funzione f
nel punto r→0 = r→(t0) ∈ γ
il limite seguente: |
ρf(r→0) = lim h→0f(r→(t0 + h)) − f(r→(t0))
Lγ(r→(t0),r→(t0+h)) .
| (8.1) |
Notare che il rapporto incrementale ha per denominatore non lo scarto
h
del parametro, ma la lunghezza dell’arco che congiunge
r→(t0) con
r→(t0 + h).
Naturalmente, il denominatore è lo scarto del parametro se il parametro è
s, il
parametro d’arco. Se l’arco rappresenta un “filo” di materiale non omogeneo e se
f(r→) rappresenta la massa
totale tra l’estremo r→(a)
e il punto r→ della
curva, allora il limite precedente, se esiste, rappresenta la usuale densità di massa del “filo”.
Però, la funzione f(r→)
non è necessariamente positiva, e potrebbe essere una componente di un
campo vettoriale, caso che si è già incontrato definendo la normale a
γ in
r→0.
Infatti, la definizione di limite (8.1) è quella usata nella definizione del versore
normale.
8.2 Gli integrali di curva
Integrali di funzioni definite su curve possono definirsi in vari modi. Per dare
definizioni significative, è necessario avere come guida degli esempi tratto dalla
fisica. Prendiamo come guida il problema di calcolare la massa totale di
un “filo”, nota la sua densità e il problema di calcolare il lavoro di una
campo di forze su un punto che si muove lungo una curva. Il primo esempio
conduce alla definizione di integrale di curva di prima specie mentre il
secondo esempio conduce alla definizione di integrale di curva di seconda
specie.
8.2.1 Integrali di curva di prima specie
Consideriamo l’esempio seguente:
Esempio 218 supponiamo che t →r→(t),
t ∈ [a,b]
parametrizzi un arco realizzato con un materiale non omogeneo, di densità
ρ(r→).
Ricordando la definizione di densità, la massa dell’arco si approssima dividendolo
in segmenti di lunghezza δ,
molto piccola, e sommando la massa dei singoli pezzetti. Il modo migliore di
fare ciò, anche se non necessariamente il più semplice dal punto di vista del
calcolo, consiste nel ricondursi alla parametrizzazione canonica, rappresentando
l’arco come s →r→(s),
s ∈ [0,L];
dividere [0,L]
con N
punti si,
si = iL∕N
e quindi costruire
∑
i=0N−1ρ(r→(s
i))[si+1 − si] = ∑
i=0N−1ρ(r→(s
i))L∕N.
Studiare quindi il comportamente di queste somme per N → +∞,
ossia quando la finezza della suddivisione dell’arco tende a zero. Questa è
niente altro che la costruzione dell’integrale della funzione s → ρ(r→(s))
sull’intervallo [0,L]. _
Sia ora f(r→)
una generica funzione, per semplicità continua. L’esempio precedente suggerisce di
definire
∫
γf(r→)ds
come segue: prima rappresentiamo l’arco in forma canonica, ossia mediante il
parametro d’arco e quindi definiamo |
∫
γf(r→)ds = def ∫
0Lf(r→(s))ds.
| (8.2) |
Questa definizione richiede che l’arco
γ
sia regolare, ed è suggerita dal significato fisico che vogliamo attribuire
all’integrale. Per il calcolo pratico conviene però evitare di rappresentare in
forma canonica l’arco. Conviene di più lavorare con la parametrizzazione
r→(t),
t ∈ [a,b],
inizialmente assegnata. Notiamo che si passa dalla parametrizzazione
r→ = r→(t)
alla parametrizzazione canonica per mezzo del cambiamento di variabile
t = t(s).
Dunque l’integrale a destra di (8.2) è, in realtà,
∫
0Lf(r→(t(s)))ds.
Ossia, in (8.2), solo per semplicità di notazioni, abbiamo sostituito il simbolo
r→(s) alla notazione più
completa r→(t(s)). La funzione
s = s(t), ossia la funzione
inversa della funzione t(s),
è derivabile, con derivata
s′(t) = |r→′(t)|.
La sostituzione di variabile s = s(t)
nell’integrale a destra di (8.2) mostra che vale: |
∫
γf(r→)ds = ∫
abf(r→(t))|r→′(t)|dt.
| (8.3) |
Se l’arco è in ℝ3,
quest’integrale è
∫
abf(r→(t))[x′ (t)]2 + [y′ (t)]2 + [z′ (t)]2dt.
Se l’arco è cartesiano, parametrizzata da
y = y(x),z = z(x),x ∈ [a,b]
allora
∫
γf(r→)ds = ∫
abf(x,y(x),z(x))1 + [y′ (x)]2 + [z′ (x)]2dx.
L’integrale appena definito si chiama integrale di curva di prima specie. La
definizione stessa mostra che esso non dipende dalla parametrizzazione
scelta per rappresentare la curva. Più ancora, se si cambia la variabile
t mediante la
trasformazione t = t(τ) = b + a − τ,
τ ∈ [a,b], il
valore dell’integrale non cambia, ossia:
Teorema 219 l’integrale di curva di prima specie non cambia né cambiando
la parametrizzazione né cambiando il verso di percorrenza dell’arco.
Il fatto che l’integrale di curva di prima specie non dipenda
dalla parametrizzazione mostra che, per ogni fissata funzione
f(τ), esso
è una proprietà geometrica della curva. Il fatto che l’integrale di curva di prima
specie non cambi valore cambiando il verso di percorrenza si scrive come
segue:
∫
−γf(r→)ds = ∫
γf(r→)ds→
Notiamo infine la disuguaglianza seguente:
Teorema 220 Sia f(r→)
una funzione continua e sia |f(r→)| < M
in ogni punto r→
del sostegno di γ.
Allora,
∫
γf(r→)ds ≤ MLγ.
In particolare, si consideri un arco γ
parametrizzato da
γ : t →r→(t),t ∈ [a,b]
ed una sua parte γ𝜖
parametrizzata da
γ𝜖 : t →r→(t),t ∈ [a,𝜖].
Vale |
lim 𝜖→a+ ∫
γ𝜖f(r→)ds = 0.
| (8.4) |
Notiamo infine che se si divide un arco
γ
γ1 e
γ2,
|
γ : t →r→(t),t ∈ [a,c]
γ1 : t →r→(t),t ∈ [a,b]; γ2 : t →r→(t),t ∈ [b,c];
|
allora vale |
∫
γf(r→)ds = ∫
γ1f(r→)ds + ∫
γ2f(r→)ds.
| (8.5) |
Osservazione 221 La definizione di integrale di curva di prima specie è
stata data assumendo che l’arco sia regolare. La (8.5) mostra come definire
l’integrale nel caso di un arco regolare a tratti: se l’arco γ
si “decompone” in (per esempio) due sottoarchi γ1
e γ2
regolari, si sceglie la (8.5) come definizione di integrale su γ. _
8.2.2 Integrali di curva di seconda specie
La definizione che ora andiamo a dare generalizza quella che si usa in fisica per il
calcolo di un lavoro.
Esempio 222 Supponiamo che in ogni punto r→
dello spazio agisca una forza F→(r→) = F→(x,y,z) = f(x,y,z)i→ + g(x,y,z)j→ + h(x,y,z)k→.
Un punto materiale di massa m
sia vincolato a descrivere un arco r→(t),
t ∈ [a,b].
Il parametro t
rappresenta ora il tempo. Si vuol valutare il lavoro compiuto dalla forza.
Dividendo ancora il percorso del punto in tanti “piccoli pezzetti”, interessa
ora valutare il prodotto scalare della forza agente su ciascun “pezzetto” per
lo spostamento del punto. Lo spostamento è un vettore, a differenza della
lunghezza percorsa che è un numero. Quando t
varia da ti
a ti+1
lo spostamento è circa r→′(t
i)(ti+1 − ti)
e quindi il lavoro compiuto è circa
[F→(r→(ti)) ⋅r→′(t
i)](ti+1 − ti).
La somma di tutti questi “lavori elementari” è
∑
i=0N−1[F→(r→(t
i)) ⋅r→′(t
i)](ti+1 − ti)
e, per calcolare il lavoro della forza bisogna studiare il comportamento
di queste somme, quando la finezza della suddivisione dell’intervallo
[a,b]
tende a zero. Si sa che in questo modo si arriva a calcolare l’integrale su
[a,b]
della funzione
F→(r→(t)) ⋅r→′(t).
Seguendo il suggerimento dell’esempio precedente definiamo l’integrale di
curva di seconda specie come segue: si assegna un campo vettoriale
V →(r→) e un arco
γ, parametrizzato
da r→(t),
t ∈ [a,b]. Si
definisce |
∫
γV →(r→) ⋅dr→ = def ∫
abV →(r→(t)) ⋅r→′(t)dt.
| (8.6) |
Nel caso particolare n = 3
e V →(x,y,z) = f(x,y,z)i→ + g(x,y,z)j→ + h(x,y,z)k→ si
trova: |
∫
γV →(r→) ⋅dr→ = ∫
ab f(x(t),y(t),z(t))x′(t)
+g(x(t),y(t),z(t))y′(t) + h(x(t),y(t),z(t))z′(t) dt.
|
Osservazione 223 Una curva semplice e chiusa si chiama anche un circuito e
l’integrale di un campo vettoriale V →(r→)
lungo una curva chiusa si chiama anche la circuitazione del campo vettoriale
lungo γ.
Quando la curva γ
è semplice e chiusa, l’integrale su γ
si indica anche col simbolo
∮
γV →(r→) ⋅dr→.
E’ immediato verificare, usando la formula di cambiamento di variabili:
Teorema 224 Il valore dell’integrale di curva di seconda specie non muta
cambiando parametrizzazione; cambia di segno cambiando verso di percorrenza.
La prima affermazione mostra che, per ogni fissato campo vettoriale
V →(R→),
l’integrale di curva di seconda specie è una proprietà geometrica della curva. La
seconda affermazione si esprime scrivendo
∫
−γV →(r→) ⋅dr→ = −∫
γV →(r→) ⋅dr→.
E’ ovvio inoltre che se si divide un arco
γ in due
archi γ1
e γ2,
|
γ : t →r→(t),t ∈ [a,c]
γ1 : t →r→(t),t ∈ [a,b]; γ2 : t →r→(t),t ∈ [b,c];
|
allora vale |
∫
γV →(r→) ⋅dr→ = ∫
γ1V (r→) ⋅dr→ + ∫
γ2V →(r→) ⋅dr→.
| (8.7) |
Esattamente come nell’osservazione 221, la (8.7), può usarsi per estendere la
definizione di integrale di curva di seconda specie ad archi regolari a tratti. L’arco
γ ottenuto
percorrendo prima γ1
e poi γ2 si indica
col simbolo γ1 + γ2.
Questo simbolo non indica soltanto l’unione insiemistica dei sostegni perché per il
calcolo dell’integrale bisogna anche specificare il verso di percorrenza. Con questa
notazione, la (8.7) si scrive anche
∫
γ1+γ2V →(r→) ⋅dr→ = ∫
γ1V (r→) ⋅dr→ + ∫
γ2V →(r→) ⋅dr→.
Quest’osservazione suggerisce la notazione seguente: siano
γ1 e
γ2
due archi, non necessariamente “sottoarchi” del medesimo. Col simbolo
γ1 + γ2 intendiamo di
percorrere prima l’arco γ1,
preso col suo verso di percorrenza, e quindi l’arco
γ2
preso col suo verso di percorrenza. Col simbolo
γ1 − γ2 si intende di percorrere
prima l’arco γ1, col suo verso
di percorrenza, e poi l’arco γ2
col verso di percorrenza negativo. Definiamo quindi |
∫
γ1+γ2V →(r→) ⋅dr→ = ∫
γ1V →(r→) ⋅dr→ + ∫
γ2V →(r→) ⋅dr→,
∫
γ1−γ2V →(r→) ⋅dr→ = ∫
γ1V →(r→) ⋅dr→ + ∫
−γ2V →(r→) ⋅dr→
= ∫
γ1V →(r→) ⋅dr→ −∫
γ2V →(r→) ⋅dr→.
|
Consideriamo ora la figura 8.1. La figura a sinistra rappresenta due archi,
γ1
e
γ2
tali che né
γ1 + γ2
né
γ1 − γ2
rappresentano un arco. La figura a destra rappresenta due archi, ciascuno col
proprio verso di percorrenza, tali che
γ1 + γ2
rappresenta un arco mentre
γ1 − γ2
non rappresenta un arco.
La figura 8.2 rappresenta a sinistra l’arco
γ1 |
γ1 : x = (1 − t)2,y = (1 − t)3,t ∈ [0, 1]
| (8.8) |
e, nel medesimo piano, l’arco γ2:
|
γ2 : x = t,y = t,t ∈ [1, 2]
| (8.9) |
ciascuno con indicato il verso di percorrenza. E’ chiaro che
γ1 + γ2 non è un
arco, mentre γ1 − γ2
lo è. La figura a destra rappresenta un caso tipico, che useremo più volte. Si noti
che la curva “esterna” e la curva “interna” sono percorse in verso opposto.
Per gli integrali di curva di seconda specie può darsi un risultato analogo
alla (8.4). Usando le medesime notazioni, si ha: |
lim 𝜖→a+ ∫
γ𝜖V →(r→) ⋅dr→ = 0,
| (8.10) |
fatto che si prova facilmente introducendo la parametrizzazione
dell’arco.
Ricordando però che l’integrale di curva di seconda specie cambia segno cambiando il
verso di percorrenza, si possono enunciare due risultati che non hanno analogo per gli
integrali di curva di prima specie. Supponiamo che un arco ripassi due volte su un
arco γ1,
percorrendolo in versi opposti. Allora, nel calcolo dell’integrale
γ1 non
dà contributo. In particolare, si consideri la figura 8.3. Nella figura, i
due lati affancati vanno pensati sovrapposti e sono il sostegno dell’arco
γ1. Sono
stati disegnati soltanto affancati per chiarezza.
Indichiamo con γs
la curva il cui sostegno è il quadrato di sinistra e con
γd quella
il cui sostegno è il quadrato di destra. Nella somma
∫
γsV →(r→) ⋅dr→ + ∫
γdV →(r→) ⋅dr→
il contributo di γ1
si elide e si trova |
∫
γs+γdV →(r→)⋅dr→ = ∫
γsV →(r→)⋅dr→+∫
γdV →(r→)⋅dr→ = ∫
γV →(r→)⋅dr→
| (8.11) |
ove γ
è la curva il cui sostegno è il rettangolo che si ottiene sopprimendo il lato comune
ai due quadrati, col verso di percorrenza indicato. Naturalmente nelle considerazioni
precedenti il fatto che le curve siano ottenute per mezzo di segmenti rettilinei non ha
alcuna importanza. Una seconda osservazione, semplice ma importante, è la seguente:
siano γ0
e γτ
(τ è
un parametro) due segmenti
γ : r→ = r→0 + tu→0,t ∈ [0,a]γτ : r→ = r→ + tu→,t ∈ [0,b].
Supponiamo che
||u→0|| = 1,||u→|| = 1.
e consideriamo i due integrali
∫
γV →(r→) ⋅dr→,∫
γτV →(r→) ⋅dr→.
Supponiamo che il campo vettoriale sia continuo e che “il segmento
γτ tenda a
sovrapporsi a γ0”.
Questo vuol dire che il secondo segmento dipende da un parametro, diciamo
τ ∈ [0, 1], ossia
che
r→ = r→(τ),u→ = u→(τ),b = b(τ).
Assumiamo che queste funzioni dipendano da
τ in
modo continuo e che sia
r→(0) = r→0,u→(0) = u→0,b(0) = a.
In tal caso:
Teorema 225 Si ha:
lim τ→0 ∫
γτV →(r→) ⋅dr→ = ∫
γ0V →(r→) ⋅dr→.
La dimostrazione è ovvia. Infatti,
Φ(t,τ) = V →(r→(τ) + tu→(τ)) ⋅u→(τ)
è una funzione continua delle due variabili
t e
τ e
inoltre
Φ(t, 0) = V →(r→0 + tu→0) ⋅u→0.
Dunque,
lim τ→0 ∫
γτV →(r→)⋅dr→ = lim τ→0 ∫
0b(τ)Φ(t,τ)dt = ∫
0aΦ(t, 0)d1 = ∫
γV →(r→)⋅r→,
si veda il paragrafo 4.2.4. In particolare,
lim τ→0 ∫
−γτV →(r→) ⋅dr→ = −∫
γ0V →(r→) ⋅dr→.
Dunque,
Corollario 226 Nelle ipotesi dette sopra si ha
lim τ→0 ∫
−γτV →(r→) ⋅dr→ + ∫
γ0V →(r→) ⋅dr→ = 0.
Ossia, Il contributo dei due integrali tende ad elidersi. Questo è il corollario che useremo
più avanti. Ora, usiamo sia la (8.10) che il Corollario 226 per giustificare l’uso
della notazione
∫
γ1+γ2
anche nel caso in cui
γ1 + γ2
non è un arco. Torniamo a considerare la figure 8.1 a sinistra. Si confronti
questa figura con la figura 8.4, a sinistra.
La figura di sinistra rappresenta una curva semplice e chiusa, chiamiamola
γ𝜖, dipendente dal
parametro 𝜖, lunghezza
degli archi (indicati con A1,𝜖,
A2,𝜖)
“rimossi” dalle ellissi di destra e di sinistra, che chiamiamo rispettivamente
γ1 e
γ2.
Dunque, |
∫
γ𝜖V →(r→) ⋅dr→ −∫
γ1+γ2V →(r→) ⋅dr→
= ∫
S1V →(r→) ⋅dr→ + ∫
S2V →(r→) ⋅dr→
−∫
A1,𝜖V →(r→) ⋅dr→ −∫
A2,𝜖V →(r→) ⋅dr→.
|
Facendo tendere 𝜖 a zero,
l’integrale sugli archi A1,𝜖,
A2,𝜖 tende
a zero per la (8.10), mentre la somma degli integrali sui due segmenti tende a zero
per il Corollario 226. Dunque,
lim 𝜖→0 ∫
γ𝜖V →(r→) ⋅dr→ = ∫
γ1+γ2V →(r→) ⋅dr→.
Ciò spega perché è necessario considerare espressioni del tipo
∫
γ1+γ2
anche nel caso in cui γ1 + γ2
non è un arco. La figura 8.4, a destra, mostra una spiegazione analoga nel caso
illustrato nella figura 8.1, a destra.
Osservazione 227 Si noti che in ambedue gli esempi, gli archi i cui integrali
approssimano quello su γ1 + γ2
sono semplici. fissato il verso di percorrenza su γ1,
quello su γ2
viene automaticamente determinato se si vuol avere un’approssimazione con
un arco semplice. In particolare, nel caso delle due curve di Jordan, una
nella regione interna dell’altra, usa prendere la curva più esterna orientata
positivamente e quindi quella più interna orientata negativamente. Più avanti
vedremo la ragione di tale scelta. _
Infine, supponiamo di avere due curve γ1
e γ2,
non necessariamente semplici:
γ1 : t →r→(t)t ∈ [a,b]; γ2 : τ →ρ→(τ)τ ∈ [α,β].
Diciamo che le due curve hanno gli stessi estremi quando
r→(a) = ρ→(α),r→(b) = ρ→(β).
In questa definizione si è tenuto conto del verso di percorrenza delle curve: i due
“primi estremi” devono coincidere ed i due “secondi estremi” devono coincidere. In
tal caso:
Lemma 228 Nelle ipotesi dette sopra,
γ1 − γ2
è una curva chiusa e
∫
γ1−γ2V →(r→) ⋅dr→ = ∫
γ1V →(r→) ⋅dr→ −∫
γ2V →(r→) ⋅dr→.
8.2.3 Integrali di curva di prima e di seconda specie
E’ interessante confrontare le definizioni degli integrali di curva di prima e seconda specie nel caso particolare
in cui V →(r→) = f(r→)i→.
In questo caso
∫
γV →(r→) ⋅dr→ = ∫
abf(x(t),y(t),z(t))x′(t)dt
mentre
∫
γfds = ∫
abf(x(t),y(t),z(t))[x′ (t)]2 + [y′ (t)]2 + [z′ (t)]2dt.
Questi due integrali non si riconducono l’uno all’altro nemmeno nel caso in cui
y(t) e
z(t) sono
identicamente zero. Infatti, in tal caso essi vengono ad essere, rispettivamente,
∫
abf(x(t),y(t),z(t))x′(t)dt,∫
abf(x(t),y(t),z(t))|x′(t)|dt.
Ciò nonostante, esiste una relazione tra gli integrali di prima e seconda specie, che ora
mostriamo. Consideriamo l’arco
γ : x(t)i→ + y(t)j→ + z(t)k→,t ∈ [a,b]
Ricordiamo che con t→(r→)
si è indicato il versore tangente alla curva nel punto
r→:
|
t→(r→(t)) = t→′(t)
|r→′(t)| = x′(t)
[x′ (t)]2 + [y′ (t)]2 + [z′ (t)]2i→
+ y′(t)
[x′ (t)]2 + [y′ (t)]2 + [z′ (t)]2j→ + z′(t)
[x′ (t)]2 + [y′ (t)]2 + [z′ (t)]2k→
|
Sia
V →(r→) = V 1(r→)i→ + V 2(r→)j→ + V (r→)k→
un campo vettoriale definito sulla curva γ.
Introduciamo la funzione |
f(t) = V →(r→(t)) ⋅ x′(t)
[x′ (t)]2 + [y′ (t)]2 + [z′ (t)]2i→
+ y′(t)
[x′ (t)]2 + [y′ (t)]2 + [z′ (t)]2j→ + z′(t)
[x′ (t)]2 + [y′ (t)]2 + [z′ (t)]2k→.
|
Si ha |
∫
γV →(r→) ⋅dr→ = ∫
γf(r→)ds.
| (8.12) |
Talvolta questa formula si trova scritta in modo diverso. Notiamo che |
n1 = x′(t)
[x′ (t)]2 + [y′ (t)]2 + [z′ (t)]2
n2 = y′(t)
[x′ (t)]2 + [y′ (t)]2 + [z′ (t)]2
n3 = z′(t)
[x′ (t)]2 + [y′ (t)]2 + [z′ (t)]2
|
sono i coseni direttori della tangente t→(r→(t)).
Per questo la formula (8.12) si trova anche scritta come segue:
∫
γV →(r→) ⋅dr→ = ∫
γ V 1n1 + V 2n2 + V 3n3 ds.
Notiamo infine che la (8.10) si può derivare dalla (8.4), usando la (8.12).
8.2.4 Integrali di curva di seconda specie e forme differenziali
L’integrale di curva di seconda specie si calcola quando è dato un campo vettoriale
V →(r→).
Dunque, possiamo vedere il campo vettoriale come operante sulla curva
γ: il campo vettoriale
V →(r→) associa un numero
alla curva γ.
Vedremo che altri campi vettoriali si usano per associare numeri alle superfici. Dunque
conviene distinguere i due casi, introducendo termini e notazioni diverse. Nel caso che
stiamo considerando, il campo vettoriale agisce su una curva. Invece di indicarlo col simbolo
V →(x,y,z) = f(x,y,z)i→ + g(x,y,z)j→ + h(x,y,z)k→, indichiamolo
col simbolo
|
f(x,y,z)dx + g(x,y,z)dy + h(x,y,z)dz.
| (8.13) |
Non vogliamo dare nessun significato particolare ai simboli
dx,
dy e
dz.
Essi, come si è notato, sono suggeriti dalla formula (8.7). Ricordiamo
però che nel caso dell’integrale su un intervallo, si conserva la notazione
“dx”
perché questa aiuta a ricordare certe formule. Come vedremo, qualcosa di analogo
accade anche in questo caso. La (8.13) si chiama 1–forma differenziale (il numero
1
ricorda che si agisce su una curva, un oggetto che,
intuitivamente,
ha dimensione 1,
come un segmento o un filo). L’integrale di curva di seconda specie si chiama
anche l’integrale di curva della 1–forma differenziale e si indica anche col
simbolo
∫
γfdx + gdy + hdz
(sottintendendo la dipendenza di f,
g e
h da
x,
y e
z).
Una regola mnemonica per ottenere la formula (8.7), per esempio nel caso
n = 3 è la seguente: si
ricordi che le funzioni f,
g ed
h dipendono
da (x,y,z). Allora, si
sostituisca x
con x(t),
y con
y(t),
z con
z(t)
ovunque queste lettere compaiono; e si interpreti
“d” come segno di
derivata; e quindi dx
si sostituisce con x′(t)dt,
dy con
y′(t)dt e
dz con
z′(t)dt. Infine, si
integri da a
fino a b,
ottenendo la (8.7). Questa è una prima buona ragione per usare la notazione delle
forme differenziali. Più avanti ne vedremo altre. Una forma differenziale si indica
spesso con una lettera greca minuscola tratta dalla fine dell’alfabeto, come
ω,
ω = fdx + gdy + hdz.
Con tale notazione l’integrale della forma differenziale si indica
∫
γω.
Infine, diciamo che la forma differenziale
ω = fdx + gdy + hdz
è di classe C1 quando sono
di classe C1 i suoi coeffcienti,
ossia le funzioni f(x,y,z),
g(x,y,z), e
h(x,y,z).
Osservazione 229 Si noti che il simbolo dx
è una forma differenziale: quella di coeffcienti f = 1
e g = h = 0.
Questa forma differenziale si chiama anche il differenziale della variabile x.
Questo termine “differenziale” ha un significato diverso da quello introdotto
al Cap. 4. Esistono relazioni tra questi due diversi concetti, che però non
illustriamo. _
8.2.5 Il flusso
Sia
V →(x,y) = f(x,y)i→ + g(x,y)j→ + h(x,y)k→
un campo vettoriale che ad ogni punto del piano
z = 0 associa un
vettore di ℝ3.
Sia 𝒟
un dominio di integrazione e supponiamo che
V →(x,y) sia continuo sulla
chiusura di 𝒟. Possiamo
pensare che il piano z = 0
sia immerso in un fluido che scorre in modo che quando una particella si trova nel punto
(x,y, 0) ivi abbia
la velocità V →(x,y)
e mantenga tale velocità dopo che ha lasciato il piano
z = 0. Il flusso attraverso
𝒟 è la quantità di fluido
che traversa 𝒟 nell’unità
di tempo. Per calcolarla
procediamo in questo modo. Approssimiamo
𝒟 mediante un numero
finito di rettangoli Ri,
come nella definizione dell’integrale doppio. Una particella che si trova in un punto
(x,y, 0) ∈ Ri
descrive nell’unità di tempo il segmento rettilineo che congiunge
(x,y, 0) con
V (x,y).
Infatti, abbiamo detto che la velocità non cambia dopo che la particella ha lasciato
il piano z = 0.
Dunque, nell’unità di tempo le particelle che escono dal rettangolo
Ri
riempiono una specie di parallelepipedo, con “faccia superiore” non piana, di base
Ri.
L’altezza varia da punto a punto, come in figura 8.5, a sinistra.
Se il rettangolo è “piccolo” l’altezza sarà circa uguale a
k→ ⋅V →(xi,yi) ove
(xi,yi)
è per esempio il vertice in basso a sinistra del rettangolo
Ri.
Dunque il volume di questo solido è approssimato da
h(Area di Ri) = [k→ ⋅V →(xi,yi)](Area di Ri).
Si noti che l’area di Ri
è positiva mentre l’altezza può anche essere negativa; ossia, il volume si prende
“con segno” perché non è indifferente che il fluido scorra verso l’alto o verso il
basso. Sommiamo ora i contributi di tutti i singoli rettangoli. Si trova una somma
integrale di quelle che definiscono l’integrale
∫
𝒟V →(x,y) ⋅k→dxdy.
Scegliamo quindi questa formula come definizione di flusso attraverso il dominio di
integrazione 𝒟.
Più avanti vedremo la definizione di flusso attraverso una superficie
non piana. Ora, definiamo il flusso di un campo piano attraverso
una curva. Supponiamo che uno strato liquido riempia il piano
(x,y) e che
il campo vettoriale
V →(x,y) = f(x,y)i→ + g(x,y)j→
rappresenti la velocità con cui una particella traversa la posizione
(x,y). Sia
γ un
arco regolare, parametrizzata da
γ : x = x(t),y = y(t),t ∈ [a,b].
Si chiama flusso del campo V →
attraverso la curva γ
la quantità di fluido che nell’unità di tempo traversa la curva. Per calcolarlo, dividiamo la
curva in archi γi
mediante i punti r→i.
Supponiamo per semplicità che questi archi abbiano tutti la medesima lunghezza
l.
Supponiamo che la particella che traversa il punto
(x,y) ∈ γ mantenga
la velocità V →(x,y)
anche dopo aver traversato la curva. Se gli archi sono “molto piccoli”,
la velocità delle singole particelle di liquido che traversano l’arco
γi si potrà approssimare
mediante V →(xi,yi).
Nell’unità di tempo, queste particelle di liquido riempiono una parte
di piano che all’incirca è un parallelogramma la cui base misura
l e la cui altezza
misura [V →(xi,yi) ⋅n→(xi,yi)]
ove n→(xi,yi) è la
normale a γ
nel punto r→i,
si veda la figura 8.5, a destra. La somma
∑
i[V →(xi,yi) ⋅n→(xi,yi)]l
è una somma integrale che per l → 0
approssima
∫
γ[V →(r→) ⋅n→(r→)]ds.
Si sceglie quindi quest’integrale come definizione di flusso di un campo vettoriale
attraverso una curva. Il flusso cambia segno cambiando il verso di percorrenza lungo la curva
perché cambiando verso di percorrenza cambia il verso sulla normale. Supponiamo ora
che la curva γ
sia semplice e chiusa. In questo caso, usa privilegiare la normale esterna
n→e:
n→e = 1
[x′ (t)]2 + [y′ (t)]2 y′(t)i→ − x′(t)j→
e quindi il flusso uscente dalla regione
Ωγ delimitata
da γ
è
∫
ab[f(x(t),y(t))y′(t) − g(x(t),y(y))x′(t)]dt = ∫
γ − gdx + fdy.
8.3 Analisi vettoriale nel piano
Mostriamo che calcolare l’integrale di certi campi vettoriali equivale al calcolo di
integrali multipli. Questo studio va sotto il nome di analisi vettoriale.
8.3.1 Una considerazione preliminare
Consideriamo una funzione
y = f(x),x ∈ [a,b].
Questa funzione identifica la curva semplice
γf : x = t,y = f(t),t ∈ [a,b].
Sia ora F(x,y) una funzione
(continua) delle due variabili x
ed y e
consideriamo l’integrale
∫
abF(x,f(x))dx.
Questo è l’integrale
∫
γfV →(r→) ⋅dr→
ove
V →(r→) = V →(x,y) = F(x,y)i→ + 0j→.
Col linguaggio delle forme differenziali,
∫
abF(x,y(x))dx = ∫
γfFdx.
Infatti, x′(t) = 1.
Analogamente, se
x = h(y),y ∈ [α,β],
sia γh la
curva identificata da questo grafico. Si ha
∫
αβF(h(y),y)dy = ∫
γhW→ ⋅dr
ove ora W→ = 0i→ + F(x,y)j→ .
E’ importante esaminare la figura 8.6 e rendersi conto dei versi di percorrenza scelti
su queste curve.
8.3.2 Formula di Green
Siano ora γf
e γg due
curve cartesiane definite sul medesimo intervallo,
y = f(x)x ∈ [a,b]
e
y = g(x)x ∈ [a,b].
Supponiamo inoltre che per ogni x ∈ (a,b)
sia
g(x) > f(x).
Indichiamo con Ω
la regione delimitata dai due grafici e dai segmenti verticali per
x = a e per
x = b
congiungenti i due grafici. Il segmento si considera nel caso in cui l’uguaglianza non
valga in uno dei due estremi. Si veda la figura 8.7, a sinistra. Si noti che la frontiera
∂Ω di
Ω è
sostegno di una curva chiusa. Ricordando le nostre convenzioni, indicheremo col
medesimo simbolo sia la curva che il suo sostegno; e quindi la indicheremo col simbolo
∂Ω e, sempre per le
nostre convenzioni, ∂Ω
è orientata in senso antiorario. Vogliamo calcolare
∫
ΩFy(x,y)dxdy.
Quest’integrale si calcola come segue:
∫
ab ∫
f(x)g(x)F
y(x,y)dydx = ∫
ab F(x,g(x)) − F(x,f(x)) dx = ∫
γgV →dr→−∫
γfV →dr→
ove
V →(x,y) = F(x,y)i→ + 0j→.
Guardando i versi di percorrenza, si vede che |
∫
ΩFy(x,y)dx = ∫
∂Ω[−V →] ⋅dr→.
| (8.14) |
Si noti che in questo calcolo il segmento verticale dà contributo nullo. Sia ora
G(x,y) una
funzione derivabile. Si vuol calcolare
∫
ΩGx(x,y)dxdy.
Proiettando la regione Ω
sull’asse delle ordinate si trova un segmento
[α,β]. La frontiera di
Ω è ancora grafico di due
funzioni, la funzione ϕ(x)
e la funzione ψ(x),
si veda la figura 8.7, a destra. I pallini con la freccia servono ad
indicare i punti nei quali i due grafici si congiungono. Il grafico di
ψ(x)
include il segmento verticale. Calcoliamo |
∫
ΩGx(x,y)dxdy = ∫
αβ ∫
ϕ(y)ψ(y)G
x(x,y)dxdy
= ∫
αβ G(ψ(y),y) − G(ϕ(y),y) dy
= ∫
γψW→ ⋅dr→ −∫
γϕW→ ⋅dr→ = ∫
∂ΩW→dr→
|
con
W→(x,y) = 0i→ + G(x,y)j→.
Si noti che in questo calcolo il segmento verticale dà contributo non nullo, mentre
darebbe contributo nullo un eventuale segmento orizzontale sulla frontiera di
Ω.
Combinando i due calcoli precedenti si trovano le due formule seguenti: |
∫
Ω Gx(x,y) − Fy(x,y) dxdy = ∫
∂Ω Fdx + Gdy,
| (8.15) |
ottenuta sottraendo la (8.14) con la (8.15). Sommandole si trova invece |
∫
Ω Gx(x,y) + Fy(x,y) dxdy = ∫
∂Ω −Fdx + Gdy.
| (8.16) |
Osservazione importante Le
formule ( 8.15) e ( 8.16) valgono anche se la regione con cui si lavora è delimitata
da più di due grafici e più in generale essa vale per qualsiasi regione di Jordan
Ωγ, delimitata
da una curva γ
regolare a tratti. Quindi non c’è più ragione di fare intervenire i trapezoidi delle
funzioni f(x)
e g(x), e
quindi di indicare con lettere maiuscole le funzioni da integrare. Per questo,
da ora in poi useremo la notazione più usuale |
∫
Ω gx(x,y) − fy(x,y) dxdy = ∫
∂Ω fdx + gdy,
∫
Ω gx(x,y) + fy(x,y) dxdy = ∫
∂Ω −fdx + gdy,
|
con le lettere minuscole. Le due formule precedenti sono
tra loro equivalenti (si passa dall’una all’altra cambiando
f in
−f).
Hanno però due diversi significati fisici, e per questo è bene conservarle
ambedue. Inoltre, ambedue la formula hanno un equivalente nello spazio
ℝ3, ma
in tal caso le due formule che si ottengono non possono ridursi l’una all’altra
con una semplice trasformazione. La formula
|
∫
Ω[gx(x,y) − fy(x,y)]dxdy = ∫
∂Ωfdx + gdy.
| (8.17) |
si chiama formula di Green.
Osservazione 230 Si noti che [gx(x,y) − fy(x,y)]
è la componente lungo il versore k→
del rotore del campo vettoriale V →(x,y) = f(x,y)i→ + g(x,y)j→ + 0k→.
La formula (8.17) si scrive quindi come
|
∫
Ω(rotV →) ⋅k→dxdy = ∫
∂ΩV → ⋅dr→ = ∫
∂Ωfdx + gdy.
| (8.18) |
Col linguaggio dei campi vettoriali la formula si interpreta come segue: il flusso del
rotore del campo vettoriale V →(x,y)
attraverso la superficie piana Ω
è uguale alla circuitazione del campo vettoriale stesso lungo ∂Ω.
Naturalmente si sottintende che ∂Ω
sia positivamente orientata. _
Osservazione 231 Torniamo a considerare la formula
|
∫
Ω gx(x,y) + fy(x,y) dxdy = ∫
∂Ω −fdx + gdy.
| (8.19) |
Quest’uguaglianza si chiama Teorema della divergenza nel piano Come si è detto, essa
è una diversa formulazione della formula di Green. Come tale, esso sotto le
medesime condizioni, ma ha una diversa interpretazione fisica, che ora illustriamo.
Consideriamo il campo vettoriale
W→(x,y) = g(x,y)i→ + f(x,y)j→.
A destra della (8.19) figura il flusso del campo vettoriale
W→, uscente dalla regione
Ω (regione interna alla curva
regolare a tratti ∂Ω). A sinistra
figura la divergenza di W→.
Dunque la (8.19) si scrive anche come
|
∫
ΩdivW→(x,y)dxdy = ∫
Ω∇⋅W→(x,y)dxdy = ∫
∂ΩW→ ⋅n→eds.
| (8.20) |
Essa si interpretra come segue: il flusso uscente da γ
del campo vettoriale W→
è uguale all’integrale su Ω
della divergenza di W→.
Quest’interpretazione in particolare spiega l’uso del termine “divergenza”. _
8.3.3 Formula di Green e forme differenziali
Si è detto che il simbolo “d”
si conserva dentro il simbolo di integrale perché aiuta a ricordare
le formule. In apparenza ciò non accade per la formula di Green.
E’ però possibile introdurre dei simboli comodi come segue. Se
f(x,y) è una
funzione, con df(x,y)
indichiamo la forma differenziale
df(x,y) = fx(x,y)dx + fy(x,y)dy.
Se ω
è una 1–forma differenziale, definiamo
dω = d fdx + gdy = fxdxdx + fydydx + gxdxdy + gydydy.
Ora introduciamo le regole seguenti: |
dxdx = 0,dydy = 0,dydx = −dxdy,
| (8.21) |
suggerite dalle regole con le quali si calcola il prodotto vettoriale, (esplicitamente
usato nella formula (8.18)):
i→ ∧i→ = 0,j→ ∧j→ = 0,j→ ∧i→ = −i→ ∧j→.
In questo modo si trova |
dω = [−fy + gx]dxdy
| (8.22) |
e questo è proprio l’integrando dell’integrale doppia in (8.17). Dunque, un
modo per ricordare la (8.17) è di scriverla come |
∫
∂Ωω = ∫
∂Ω[fdx + gdy] = ∫
Ωd[fdx + gdy] = ∫
Ωdω.
| (8.23) |
Osservazione 232 Introdurremo più avanti il Teorema di Stokes in ℝ3,
che vale per curve che sono bordo di calotte. Il Teorema di Green è il caso
particolare del Teorema di Stokes in ℝ3
che si ottiene quando la curva è una curva di Jordan e quando la superficie
è la regione interna alla curva. _
La 2-forma
differenziale dω
si chiama anche il differenziale esterno (o più brevemente il differenziale) della
1-forma
ω.
8.3.4 Le forme differenziali e le aree piane
Scriviamo la formula di Green scegliendo come forma differenziale la seguente:
ω = −ydx + xdy
Si trova
∫
γ − ydx + xdy = ∫
Ωγ2dxdy
e l’integrale a destra è il doppio dell’area di
Ωγ. Si
trova quindi:
Teorema 233 Sia
γ
una curva di Jordan orientata positivamente e sia
Ωγ
la sua regione interna. L’area di
Ωγ
è data da
1
2 ∫
γ − ydx + xdy.
Questa formula è un caso particolare del Teorema di Green e quindi si prova
calcolando
∫
Ωγ1dxdy
mediante successive integrazioni per parti. E’ però interessante
vedere un’argomento geometrico che conduce a questa formula. Sia
γ:
t →r→(t),
t ∈ [a,b]
un arco piano regolare, semplice e chiuso e sia Ωγ
la sua regione interna. Per semplicità di esposizione,
assumiamo che l’origine degli assi appartenga alla regione interna
Ωγ
(caso a cui ci si può sempre ricondurre mediante una traslazione).
Si consideri la figura 8.8. Il punto r→(t)
varia sull’arco. Dividiamo l’intervallo [a,b]
in “piccoli” intervalli, dividendolo con i punti
ti (equidistanti per semplicità).
Approssimiamo l’arco r→(t),
t ∈ [ti,ti+1] col
segmento di tangente
r→ = r→(ti) + r→′(t
i)(t − ti),t ∈ [ti,ti+1]
come in figura 8.8. Consideriamo i triangoli di vertici l’origine, il punto
r→(ti) e il
secondo estremo del segmento di tangente. Si potrebbe provare che quando la finezza della partizione di
[a,b]
tende a zero, la somma delle aree di questi triangoli tende all’area di
Ωγ, pur di
intendere l’area di tali triangoli con segno, in modo da cancellare eventuali parti di area coperte più
volte. L’area (con segno) di ciascuno di questi triangoli è la metà della componente lungo l’asse
z del prodotto
vettoriale dei vettori r→(ti)
e r→′(ti)(ti+1 − ti). Per approssimare
l’area di Ωγ
dobbiamo quindi sommare la componenti lungo l’asse verticale di
1
2r→(ti) ∧r→′(t
i)(ti+1 − ti).
Si trova così
1
2∑
i=0N−1[x(t
i)y′(t
i) − y(ti)x′(t
i)](ti+1 − ti).
Al tendere a zero della finezza della partizione queste somme approssimano |
1
2∫
ab[x(t)y′(t) − y(t)x′(t)]dt = 1
2∫
γ[−ydx + xdy].
| (8.24) |
L’argomento precedente non è rigoroso, ma può pienamente
giustificarsi. Chiediamoci ora se l’integrale precedente restituisce l’area di
Ωγ,
oppure l’area col segno negativo. Si vede subito dalla figura 8.8 che la somma delle aree
dei triangoli viene positiva quando l’orientazione della curva è concorde con quella di
ℝ2; ossia
quando la curva è orientata positivamente.
8.3.5 Le estensioni
La formula di Green è stata provata per una regione molto particolare. Si è
già notato che essa vale sotto condizioni molti più generali. E infatti:
Teorema 234 Le uguaglianze (8.18) e (8.16) valgono per ogni regione Ωγ,
con γ
curva regolare a tratti e per ogni coppia di funzioni f(x,y),
g(x,y)
di classe C1(Ω
γ),
continue sulla chiusura di Ωγ.
Mostriamo ora un’estensione importante di queste formule. Quest’estensione
è suggerita dalla figura (8.4). Si tratta di un’estensione di
queste formule a regioni delimitate da più curve, come nel caso
rappresentato dalla figura 8.9, a sinistra, dove le curve sono due,
γ1
e γ2,
il sostegno dell’una contenuto nella regione interna all’altra.
Chiamiamo Ω la regione
delimitata dalle curve γ1
e γ2 e
sia V →(x,y) ∈ C1(Ω)
un campo vettoriale continuo sulla chiusura di
Ω. Introduciamo
due segmenti, S1
ed S2,
come nella figura a destra, e due piccoli tagli uno su
γ1 e l’altro
su γ2,
in corrispondenza a tali segmenti. Si ottiene in questo modo una curva
γ̃ che
verifica sia le condizioni della formula di Green che quelle della formula della
divergenza. Vale quindi |
∫
Ωγ̃[gx(x,y) − fy(x,y)]dxdy = ∫
γ̃fdx + gdy,
∫
Ωγ̃[gx(x,y) + fy(x,y)]dxdy = ∫
γ̃V → ⋅n→eds.
|
Quando S1
ed S2 tendono
l’uno all’altro gli integrali lungo i due segmenti si elidono, gli integrali sui due tagli
tendono a zero (si ricordino la (8.10) e il Teorema 226.) e l’integrale sulla regione interna
a γ̃ tende
all’integrale su Ω.
Si trova quindi
|
∫
Ω(rotV →) ⋅k→dxdy = ∫
γ2V → ⋅dr→ −∫
γ1V → ⋅dr→,
∫
ΩdivV →dxdy = ∫
γ2V → ⋅n→eds −∫
γ1V → ⋅n→eds.
|
Si noti che il segno negativo viene perchè la curva interna va considerata
orientata negativamente, mentre abbiamo convenuto che nel simbolo
∫
γ la
curva chiusa debba essere orientata positivamente. Nel caso particolare in cui si
abbia
divV →(r→) = ∇⋅V →(r→) = 0,
La formula precedente mostra che Se la divergenza di un campo
vettoriale è nulla, il flusso del campo vettoriale entrante attraverso
γ1 è uguale a quello
uscente attraverso γ2.
Si discutano risultati analoghi ai precedenti, nel caso in cui la regione delimitata
dalla curva più esterna contenga vari “buchi”, ciascuno delimitato da una curva di
Jordan regolare a tratti.
Osservazione 235 Si osservi che se il campo vettoriale è di classe
C1(Ω
γ1)
allora le relazioni precedenti si ottengono semplicemente per differenza:
|
∫
Ω∇⋅V →(r→) ⋅dxdy = ∫
Ωγ
1∇⋅V →(r→) ⋅dxdy −∫
Ωγ
2∇⋅V →(r→) ⋅dxdy
= ∫
γ1W→ ⋅n→eds −∫
γ2W→ ⋅n→̃e→ds.
|
In questa formula, n→̃e→
è la normale esterna ad Ωγ2
e quindi interna ad Ω;
e γ2
è percorsa in senso positivo ripetto a Ωγ2
e quindi in senso negativo rispetto a Ω. _
8.4 Integrali di superficie
La lunghezza di un arco è stata definita nel paragrafo 6.1.2. Invece, non si è
definita l’area di una calotta. Questo è il primo argomento che ora studiamo.
Definiremo poi l’integrale su una calotta. Come nel caso delle curve, vedremo che
serve definire due tipi diversi di integrali.
8.4.1 Area di una calotta
Consideriamo una calotta r→(u,v)
con (u,v) variabili in una
regione Ωγ delimitata da una
curva semplice chiusa γ,
regolare a tratti. Sia inoltre r→(u,v)
di classe C1(Ω
γ). Ricordiamo
che la chiusura di Ωγ
è un dominio di integrazione. Dunque, è possibile approssimare la regione
Ωγ
mediante tanti piccoli rettangoli con i lati paralleli agli assi coordinati, si vedano
l’osservazione 204 e il paragrafo 7.1.3. fissiamo l’attenzione su uno di questi
rettangoli e sulla sua immagine sulla superficie (si veda la figura 8.10).
Per semplicità di notazioni, supponiamo che esso sia un quadrato col vertice a sinistra in
basso nel punto (0, 0)
e che al punto (0, 0)
corrisponda il punto (0, 0, 0)
(si noti che questo non è il caso illustrato dalla figura). Consideriamo il lato
(t, 0) del quadrato,
0 ≤ t ≤ τ. Ad esso corrisponde una
curva r→(t, 0) sulla superficie, la
cui tangente in (0, 0, 0) è parallela
al vettore r→u(0, 0). Consideriamo
il segmento di tangente r→u(0, 0)t,
0 ≤ t ≤ τ.
In modo analogo, a partire dall’altro lato di vertice
(0, 0), arriviamo a
considerare il segmento r→v(0, 0)t,
0 ≤ t ≤ τ. Questi due
segmenti (uscenti da (0, 0, 0))
appartengono al piano tangente e in generale non stanno sulla superficie; ma, se
τ è
“piccolo” il parallelogramma che essi individuano differisce “per poco”
dall’immagine del quadrato sulla superficie. Dunque l’area di tale parallelogramma
approssima l’area della parte di superficie che viene descritta quando
(u,v)
varia nel quadrato. L’area del parallelogramma è
τ2 ⋅|r→
u(0, 0) ∧r→v(0, 0)| = τ2|N→(0, 0)|. Si
ripeta questo argomento per ciascuno dei rettangoli e si sommino i risultati. Quello
che si trova è una somma di Riemann per l’integrale doppio la funzione
|N→(u,v)|. Ciò
giustifica la definizione seguente:
Definitione 4 Sia
(u,v) →r→(u,v)(u,v) ∈ Ω
una superficie regolare. Sia
γ
una curva semplice e chiusa con sostegno in
Ω
e sia
Σ : (u,v) →r→(u,v)(u,v) ∈ Ωγ
la calotta corrispondente. Si chiama area della calotta
Σ
il numero
∫
Ωγ|N→(u,v)|dudv.
Usando la regola per il cambiamento di coordinate degli integrali doppi e il
Teorema 202 si potrebbe provare:
Teorema 236 Due superfici equivalenti, ossia che differiscono solo per
la parametrizzazione, hanno la medesima area. Inoltre, l’area non muta
cambiando l’orientazione della superficie.
Se la superficie è data in forma cartesiana,
z = f(x,y),
la sua area è
∫
Ωγ1 + fx 2 (x, y) + fy 2 (x, y)dxdy.
Come ulteriore caso particolare, consideriamo il caso di una superficie di rotazione,
descritta da
z = f(x2 + y2)ωγ = DR = x2 + y2 ≤ R2 .
In questo caso, |
∂
∂xf(x2 + y2) = x
x2 + y2f′(x2 + y2),
∂
∂yf(x2 + y2) = y
x2 + y2f′(x2 + y2)
|
e quindi l’area è data da |
∫
DR
1 + f′(x2 + y2) 2dxdy
∫
02π ∫
0Rr1 + f′ (r) 2drd𝜃 = 2π∫
0Rr1 + f′ (r) 2dr.
|
Anche questa formula si chiama formula di Guldino e si interpreta facilmente. Dividendo
l’intervallo [0,R]
mediante i punti ri,
l’integrale si approssima mediante la somma dei numeri
2πri (ri+1 − ri)1 + f′ (ri ) 2
e questa è l’area di un tronco di cono “iscritto” nella superficie, come in
figura 8.11
8.4.2 Densità superficiale
Si abbia una funzione che ad ogni calotta di una superficie associa un
numero. Per esempio, se la superficie è realizzata con una lamiera,
la funzione che ad una calotta della superficie associa la sua massa
o, nelle applicazioni all’elettrologia, la sua carica. Indichiamo con
m(Σ)
questa funzione. La densità (di massa, di carica ecc.) media su
Σ è il
numero
ρ(Σ) = m(Σ)
A(Σ).
In questa formula, A(Σ)
è l’area della calotta Σ.
Vogliamo ora passare dalla densità media alla densità puntuale. Per questo,
supponiamo che la superficie sia parametrizzata da
(u,v) →r→(u,v),(u,v) ∈ Ω
e supponiamo che la superficie sia semplice, ossia supponiamo
che questa trasformazione sia iniettiva. fissiamo un punto
r→0 sulla
superficie,
r→0 = r→(u0,v0).
Sia Ql un quadrato
di lato l il cui
centro è (u0,v0)
e sia 𝒞l
l’immagine del quadrato sulla superficie. Si considera quindi il limite
ρ(r→0) = lim l→0m(𝒞l)
A(𝒞l).
Se questo limite esiste finito, lo chiamiamo la densità della funzione
m. In realtà
questa definizione è più delicata di quanto possa sembrare perchè per il calcolo
del limite si sono privilegiati i quadrati. Niente garantisce che se si fossero scelti dei
dischi
si sarebbe trovato il medesimo limite e in effetti generalmente ciò non
avviene. Diciamo che, sotto “ipotesi di regolarità” della funzione
m ciò
non accade. Ma non abbiamo i mezzi necessari per specificare quali siano queste
ipotesi. Il procedimento inverso a questo, porta a definire gli integrali di superficie
di prima specia.
8.4.3 Integrali di superfici di prima specie
Cosìcome per le curve, anche sulle superfici si definicono due tipi
diversi di integrali. Il primo è suggerito dal problema del calcolo
della massa di una superficie, quando si conosce la la densità
ρ, che può
variare da punto a punto. Ricordando la definizione di densità, per esempio di massa,
non meraviglia che per ritrovare la massa totale della calotta che si ottiene quando
(u,v) varia in una regione
Ωγ, delimitata da una
curva di Jordan γ,
si debba calcolare
∫
Ωγρ(x(u,v),y(u,v),z(u,v))|N→(u,v)|dudv.
In generale, un integrale della forma |
∫
Ωγf(x(u,v),y(u,v),z(u,v))|N→(u,v)|dudv.
| (8.25) |
(con f(x,y,z)
funzione continua definita sulla calotta) si chiama integrale di superficie
di prima specie o semplicemente integrale superficiale. E’ chiaro che
il valore dell’integrale non cambia cambiando l’orientazione della
superficie, dato che nell’espressione dell’integrale figura non direttamente
N→, ma il
suo modulo. Oltre a ciò si potrebbe provare:
Teorema 237 L’integrale di superficie di prima specie non muta cambiando
parametrizzazione.
Invece di usare la notazione (8.25) si usa in genere la notazione
∫
Σf(x,y,z)dΣoppure∫
Σf(x,y,z)dA
(A iniziale di “area”.
Talvolta si scrive dS).
8.4.4 Integrale di superficie di seconda specie
L’integrale di superficie di seconda specie è suggerito dal calcolo
del flusso attraverso una superficie, che ora definiamo. Sia
V →(x,y,z) = f(x,y,z)i→ + g(x,y,z)j→ + h(x,y,z)k→ un
campo vettoriale che però ora non interpretiamo come campo di forze. Piuttosto
pensiamo che un fluido riempia tutto lo spazio e che la particella che passa per il punto
(x,y,z) ci passi con
velocità V →(x,y,z).
Vogliamo calcolare la quantità di fluido che, nell’unità di tempo, traversa la
superficie. Approssimiamo ancora la superficie con tanti piccoli parallelogrammi che
giacciono sui piani tangenti, come abbiamo fatto per il calcolo dell’area. Sia
𝒫 uno di essi.
La quantità di fluido che nell’unità di tempo lo attarversa è il volume del parallelepipedo
che ha 𝒫
per base e la cui altezza è, circa,
N→(x0,y0,z0)
|N→(x0,y0,z0)|⋅V →(x0,y0,z0)
(“circa”, perché il campo vettoriale non è costante su
𝒫). Si
veda la figura 8.12.
Il volume va calcolato ora con segno perché non è indifferente che il fluido
passi dall’una all’altra parte della superficie, ed è dato da
V →(x0,y0,z0) ⋅N→(x0,y0,z0)
(si ricordi che |N→(x0,y0,z0)|
è circa l’area di 𝒫
e che N→(x0,y0,z0)
è l’area “con segno”). Sommando i contributi di tutti i parallelogrammi
si trova una delle somme di Riemann che approssimano l’integrale di
V →(x,y,z) ⋅N→(x,y,z). Ciò
suggerisce di definire l’integrale di superficie di seconda specie |
∫
ΩV →(x(u,v),y(u,v),z(u,v)) ⋅N→(x(u,v),y(u,v),z(u,v))dudv.
| (8.26) |
Una notazione più semplice che si usa per indicare questo integrale è
In questa notazione si sottintende la dipendenza da
u e da
v. Si
noti che l’integrale di superficie di seconda specie è uguale a
∫
ΣV →(r→) ⋅n→(r→)dA
con n→(r→)
il versore normale alla superficie. Si prova:
Teorema 238 Il valore dell’integrale di superficie di seconda specie non
muta cambiando la parametrizzazione della superficie. Esso cambia di segno
cambiando l’orientazione.
Osservazione 239 L’integrale di superficie di seconda specie è un “integrale
orientato”: esso cambia segno cambiando il verso della normale, ossia l’orientazione
della superficie. Consideriamo ora il caso particolare in cui la superficie Σ
è un dominio di integrazione, Σ = 𝒟,
del piano (u,v)
e quindi è parametrizzata da
x = u,y = v,z = 0,(u,v) ∈ Σ.
Sia inoltre
V →(x,y,z) = V →(x,y) = h(x,y)k→.
In questo caso, se la superficie è orientata positivamenta
∫
ΣV →(x,y) ⋅dΣ = ∫
Σh(x,y)dxdy = ∫
𝒟h(x,y)dxdy,,
l’usuale integrale doppio di h(x,y).
Se però la superficie è orientata negativamente, la normale punta verso il
basso e
∫
ΣV →(x,y) ⋅dΣ = ∫
Σh(x,y)dydx,
e questo vale
−∫
𝒟h(x,y)dxdy,
l’usuale integrale doppio cambiato di segno. _
8.4.5 Integrale di superficie di seconda specie e forme differenziali
Sia nel calcolo del lavoro, integrale di curva di prima specie, che nel calcolo del
flusso, integrale di superficie di seconda specie, interviene un campo vettoriale, ma
le proprietà fisiche di tali campi sono sostanzialmente diverse. E’ quindi utile
individuare un formalismo matematico che permetta di distinguere un caso
dall’altro e di distinguere anche visivamente se un campo vettoriale si vuol usare
per il calcolo di un’integrale di curva o di superficie. Per arrivare a ciò, vediamo
una formula esplicita per il calcolo dell’integrale (8.27), più esplicita della
formula (8.26). Ricordiamo che |
N→(u,v) = (xui→ + yuj→ + zuk→) ∧ (xvi→ + yvj→ + zvk→)
= [yuzv − zuyv]i→ + [zuxv − xuzv]j→ + [xuyv − yuxv]k→.
|
L’espressione esplicita di (8.27) è |
∫
Ω f(x,y,z)[yuzv − zuyv] + g(x,y,z)[zuxv − xuzv] + h(x,y,z)[xuyv − yuxv] dudv
| (8.28) |
(la dipendenza di x,
y,
z da
u e da
v non si è indicata
per brevità). Se V →(x,y,z) = f(x,y,z)i→ + g(x,y,z)j→ + h(x,y,z)k→
è il campo vettoriale che si vuol integrare su una superficie, indichiamolo col
simbolo |
fdydz + gdzdx + hdxdy.
| (8.29) |
Scriviamo inoltre |
dx = xudu + xvdv,dy = yudu + yvdv,dz = zudu + zvdv.
| (8.30) |
Usando le “regole di calcolo” (8.21) è ora facile ricostruire
l’espressione dell’integrale (8.28). L’integrando si ottiene sostituendo
le (8.30) in (8.29) e usando le (8.21) (rispetto ai simboli
du e
dv). Si
trova: |
dydx =yuzududu + yuzvdudv + yvzudvdu + yvzudvdv
=(yuzv − yvzu)dudv
dzdx =(zuxv − zvxu)dudv
dxdy =(xuyv − xvyu)dudv
|
come serve per il calcolo dell’integrale (8.28). Un’espressione della forma (8.29) si chiama
una 2-forma
differenziale (il numero 2 ricorda che si vuole integrarla su
una superficie, intuitivamente un “foglietto” di dimensione
2.) Anche
le 2-forme
differenziali si indicano con lettere greche minuscole,
ω = fdydz + gdzdx + hdxdy.
Completiamo le regole (8.21) imponendo: |
dxdx = 0, dydy = 0, dzdz = 0, dyd x = −d xd y,dzd x = −d xd z,dzd y = −d yd z.
| (8.31) |
(anche queste regole sono suggerite dalle regole del prodotto vettoriale).
Con queste notazioni, la (8.28) si ottiene dalla (8.29) sostituendo
x,
y,
z con
x(u,v),
y(u,v),
z(u,v);
usando le regole di calcolo precedenti e quindi integrando su
Ω.
8.5 Analisi vettoriale nello spazio
Studiamo ora l’analisi vettoriale nello spazio.
8.5.1 Formula della divergenza e formula di Gauss
L’uguaglianza (8.23) correla le 1-forme
differenziali e gli integrali su aree piane. Mostriamo che
esiste una formula analoga, che correla gli integrali delle
2–forme differenziali
(ossia, i flussi di campi vettoriali) e gli integrali di volume. Limitiamoci a considerare il caso
di regioni Ω
convesse. Non è diffcile mostrare che la formula che troveremo vale anche se la
regione Ω
può rappresentarsi come unione o differenza di regioni convesse. Cosìcome abbiamo
fatto per la riduzione degli integrali multipli ad integrali iterati, indichiamo con
Ωz la proiezione
sul piano (x,y)
di Ω,
Ωz = {(x,y)|esiste z tale che(x,y,z) ∈ Ω}.
Analogamente definiamo Ωx
ed Ωy. Sia
(x,y) ∈ Ωz. La retta verticale
per (x,y) interseca
Ω in un segmento
[ϕ(x,y),ψ(x,y)]. Richiediamo
che le funzioni ϕ(x,y),
ψ(x,y) siano
di classe C1.
Proprietà analoghe richiediamo anche per le intersezioni con le rette parallele
agli assi delle ascisse e delle ordinate. Sotto queste condizioni, la regione
Ω viene ad
essere delimitata da “pezzi” di superfici regolari. In ciascun punto di tali superfici è
possibile definire la normale. La normale non sarà generalmente definita nei punti
in cui due “pezzi” diversi si congiungono. Per semplicità noi supporremo che in ogni
punto di ∂Ω
sia possibile definire la retta normale. Vedremo più avanti
come indebolire questa condizione. Consideriamo un punto
r→0 = (x0,y0,ψ(x0,y0)) della superficie
superficie z = ψ(x,y). Se un punto
r→1 = (x1,y1,z1) di questa retta appartiene
ad Ω, tutto il segmento
che lo congiunge a r→0
è in Ω
perch’e Ω
è convessa. Dunque, è possibile definire la normale entrante e la normale uscente da
Ω nel punto
r→0 . Applichiamo
in ogni punto P
di Ω la normale
uscente ad Ω
in tale punto. Tale vettore normale indichiamo col simbolo
N→e(P) (l’indice
“e”
indica “normale esterna” o uscente dalla superficie).
Per esempio, fissiamo l’attenzione sulla “parte inferiore” della superficie
Ω in
fig. 8.13, parametrizzata da
xi→ + yj→ + ϕ(x,y)k→(x,y) ∈ Ωz.
Nel caso specifico si tratta di una sfera e se ne considera la parte “sotto
l’equatore”. Abbiamo definito la normale
N→(x,y) = (i→+ϕx(x,y)k→)∧(j→+ϕyk→) = −ϕx(x,y)i→−ϕy(x,y)j→+k→.
Essendo positivo il coeffciente di k→,
la normale punta verso l’alto. Dunque entra in
Ω.
Invece, noi vogliamo la normale che esce da
Ω. Dobbiamo quindi
cambiare segno alla N→(x,y)
e scegliere
−N→(x,y) = −(i→+ϕx(x,y)k→)∧(j→+ϕyk→) = ϕx(x,y)i→+ϕy(x,y)j→−k→.
Definitione 5 Indicheremo con N→e(r→)
la normale nel punto r→
alla superficie Σ
che racchiude Ω,
orientata verso l’esterno di Ω.
_
Vediamo esplicitamente un esempio.
Esempio 240 La superficie sia la sfera x2 + y2 + z2 = 1.
Si tratta quindi di una superficie assegnata in modo implicito. I due emisferi
superiore ed inferiore sono parametrizzati rispettivamente da
z = 1 − x2 − y2z = −1 − x2 − y2,x2 + y2 < 1.
Si vede facilmente che se si vuole la normale esterna, ossia uscente da Ω,
bisogna parametrizzare l’emisfero superiore scegliendo prima x
e poi y;
nell’emisfero inferiore bisogna scegliere prima y
e poi x. _
Sia ora T(x,y,z)
una funzione derivabile. Calcoliamo |
∫
Ω ∂
∂zT(x,y,z)dxdydz = ∫
Ωz ∫
ϕ(x)ψ(x) ∂
∂zT(x,y,z)dzdxdy
= ∫
ΩzT(x,y,ψ(x,y))dxdy −∫
ΩzT(x,y,ϕ(x,y))dxdy.
|
La normale esterna alla superficie di
Ω, nei
punti (x,y,ψ(x,y)),
rispettivamente (x,y,ϕ(x,y)),
è: |
N→e(x0,y0,z0) = −ψx(x0,y0)i→ − ψy(x0,y0)j→ + k→,
N→e(x0,y0,z0) = ϕx(x0,y0)i→ + ϕy(x0,y0)j→ −k→
|
Dunque
∫
Ω ∂
∂zT(x,y,z)dxdydz = ∫
ΩzTk→ ⋅N→edxdy.
Indichiamo con Σz le due
calotte di parametrizzazione ϕ(x,y)
e ψ(x,y). Con questa
notazione e chiamando n→e
il versore
n→e = N→e
|n→e|,
l’ultimo integrale è uguale a
∫
ΣzTk→ ⋅n→edΣ = ∫
ΣzTk→ ⋅dΣ →.
Si noti che i grafici delle funzioni ϕ(x,y)
e ψ(x,y) possono non esaurire
tutta la frontiera di Ω,
ma una parte della frontiera che non appartiene a tali grafici è parte
di un cilindro verticale. Ha quindi per normale un vettore ortogonale a
k→ e
quindi non dà contributo al calcolo dell’integrale. In modo analogo si mostra che
|
∫
Ω ∂
∂yS(x,y,z)dxdydz = ∫
ΩySj→ ⋅N→edxdy = ∫
ΣySj→ ⋅n→edΣ,
∫
Ω ∂
∂xR(x,y,z)dxdydz = ∫
ΩxRk→ ⋅N→edydz = ∫
ΣxRi→ ⋅n→edΣ
|
(le definizioni di Σx
e Σy sono analoghe
a quella di Σz).
Sommando i tre integrali si trova
Teorema 241 (della divergenza) Sia
Ω una
regione convessa e limitata, la cui frontiera è sostegno di una superficie regolare.
Vale
|
∫
Ω ∂
∂xR(x,y,z) + ∂
∂yS(x,y,z) + ∂
∂zT(x,y,z) dxdydz
= ∫
Ωdiv Ri→ + Sj→ + Tk→dxdydz = ∫
Ω∇⋅Ri→ + Sj→ + Tk→dxdydz
= ∫
∂Ω{Ri→ + Sj→ + Tk→}⋅dΣ →.
|
La superficie Σ
è orientata scegliendo la normale usente da
Ω.
Nell’ultimo integrale si intende che la superficie è orientata mediante la normale
esterna.
Il teorema della divergenza ha la seguente interpretazione: il flusso di un campo
vettoriale uscente da una superficie è uguale all’integrale di volume della divergenza del
campo vettoriale stesso. Il flusso è positivo quando il campo vettoriale “esce” da
Ω.
In tal caso, l’integrale della divergenza è positivo, e ciò, come si
è già notato, spiega l’uso del termine “divergenza”. Consideriamo
ora una caso particolare: supponiamo che il campo vettoriale
V →(x,y,z) sia il gradiente
di una funzione ϕ(x,y,z),
a valori reali. In questo caso, |
div∇ϕ(x,y,z) = ∇⋅∇ϕ(x,y,z)
= ϕxx(x,y,z) + ϕyy(x,y,z) + ϕzz(x,y,z) = Δϕ(x,y,z)
|
e quindi si trova:
∫
ΩΔϕ(x,y,z)dxdydz = ∫
∂Ω∇ϕ ⋅dΣ →.
Questo caso particolare del Teorema della divergenza va sotto il nome di Formula di
Gauss.
In fisica hanno importanza queli campi vettoriali che hanno flusso
nullo attraverso ogni superficie chiusa. Tali campi si chiamano campi
solenoidali Una condizione suffciente perchè un campo vettoriale sia
solenoidale è che la sua divergenza sia nulla. Questa condizione è
solo suffciente come prova l’esempio seguente:
F→(x,y,z) = x
(x2 + y2 + z2)3∕2i→+ y
(x2 + y2 + z2)3∕2j→+ z
(x2 + y2 + z2)3∕2k→
(proporzionale al campo elettrico di una carica
puntiforme, il cui flusso attraverso una sfera
concentrata nella carica non è nullo, nonostante che
∇⋅F→(x,y,z) = 0).
Se accade che il campo è ovunque definito e di classe
C1
allora il campo è solenoidale se e solo se la sua divergenza è nulla. Vediamo ora di scrivere il il Teorema della divergenza con l’uso del simbolismo delle
forme differenziali. Sia
ω = Rdydz + Sdzdx + Tdxdy.
Usando le regole (8.31) si trova |
dω = (Rx + Sy + Tz)dxdydz.
| (8.32) |
Per uniformità, usa chiamare “3–forma differenziale” un’espressione della
forma
f(x,y,z)dxdydz.
Essa è niente altro che la funzione scalare
f(x,y,z). Si usa
questa notazione, per intendere che questa funzione va integrata su una regione dello
spazio ℝ3,
con l’avvertenza però che il segno cambia per ogni inversione nell’ordine dei tre simboli
dx,
dy e
dz.
Ossia, per esempio, |
f(x,y,z)dxdydz = −f(x,y,z)dydxdz,
f(x,y,z)dxdydz = f(x,y,z)dydydx.
|
Con queste notazioni, il Teorema della divergenza si scrive
In questa formula si intende di aver orientato la normale verso l’esterno di
Ω.
Estensioni
Estendiamo ora la formula della divergenza a regioni più generali. Consideriamo due
casi:
-
- Caso 1.
Supponiamo di avere due regioni Ω1
e Ω2 su
ciascuna delle quali vale il teorema della divergenza, e supponiamo che
- le due regioni non siano contenute l’una nell’altra, ma si intersechino.
Indichiamo con Ωd e
Ωu rispettivamente l’unione delle
due regionie la differenza Ω1 − Ω2:
|
Ωd = {r→|r→ ∈ Ω1,e ancher→∉Ω2},
Ωu = {r→|r→ ∈ Ω1oppurer→ ∈ Ω2}.
|
Supponiamo che una 2-forma
differenziale ω (equivalentemente,
un campo vettoriale V →(r→))
sia di classe C1(ℝ3).
Consideriamo la regione Ωd.
In questa regione, la (8.33) diviene: |
∫
Ωddω = ∫
Ω1dω −∫
Ω1∩Ω2dω = ∫
∂Ω1ω −∫
∂(Ω1∩Ω2)ω.
| (8.34) |
Si noti che l’uguaglianza vale perché Ω1 ∩ Ω2
è convessa, come unione di regioni convesse. La figura 8.15 mostra una sezione dell’insieme su cui si lavora. L’insieme
∂(Ω1 ∩ Ω2) è unione di due parti:
una parte della frontiera di Ω1
che chiamiamo Γ1 e una
parte della frontiera di Ω2
che chiamiamo Γ2.
Chiamiamo invece Σ1
e Σ2 le parti rimanenti
delle frontiere di Ω1
e di Ω2.
Proseguiamo ora le uguaglianze in (8.34). Si ha: |
∫
∂Ω1ω −∫
∂(Ω1∩Ω2)ω = ∫
Σ1ω + ∫
Γ1ω −∫
Γ1ω + ∫
Γ2ω
∫
Σ1ω + ∫
Γ2ω = ∫
∂(Ω1−Ω2)ω.
|
Ciò prova che la formula della divergenza vale anche nella regione non convessa ottenuta
come differenza di due regioni convesse.
Osservazione 242 Si noti un problema nel calcolo precedente: la frontiera di
Ω1 − Ω2
non è regolare e quindi l’uguaglianza in (8.35) non è perfettamente giustificata da quanto
abbiamo detto prima. Però la dimostrazione della formula della divergenza si ottiene con
una catena di integrazioni per parti, che possono giustificarsi anche nel caso in esame. _
-
- Caso 2.
Passiamo ora a considerare la regione Ω = Ω1 ∪ Ω2.
Si noti che Ω
non è una regione convessa e che
∂Ω = Σ1 ∪ Σ2
ove Σ1 è la parte della
frontiera di Ω1 che non
è contenuta in Ω2;
Σ2 è la parte della
frontiera di Ω2 che non
è contenuta in Ω1.
Sia inoltre
Γ1 = [∂Ω1] ∩ Ω2,Γ2 = [∂Ω2] ∩ Ω1.
La figura 8.14 mostra, separatamente a sinistra ed a destra, le due regioni con indicate le varie
parti della frontiera. Le stelle indicano la curva in cui si intersecano. La figura 8.16 mostra
l’unione delle due regioni, con la parte delle due frontiere “visibile dall’esterno”. E’ chiaro
che
Σ = ∂Ω = Σ1 ∪ Σ2.
Però, né la regione è convessa, né la frontiera è regolare.
Ciò nonostante, argomenti analoghi a quelli visti sopra portano a
concludere che il teorema della divergenza vale anche nella regione
Ω = Ω1 ∪ Ω2.
Osservazione 243 Si potrebbe provare che la classe delle regioni per cui vale il Teorema
della divergenza è assai ampia: tutte le regioni limitate la cui frontiera è una superficie
regolare orientabile. Discuteremo il concetto di orientabilità di una superficie più avanti.
Per ora diciamo soltanto che se una superficie regolare ha per sostegno la frontiera di una
regione limitata, essa si dice superficie chiusa. _
-
- Caso 3.
E’ il caso in cui la regione Ω2 sia
contenuta nella regione Ω1,
come può essere il caso di due palle concentriche. In tal caso è facile vedere che la (8.35) vale
ancora. Però ora
∂(Ω1 − Ω2) = ∂Ω1 ⋃
∂Ω2 .
La normale va scelta uscente da Ω1 − Ω2.
E quindi sulla frontiera di Ω1 va
scelta la normale uscente da Ω1;
sulla frontiera di Ω2 va scelta
la normale entrante in Ω2.
8.5.2 La formula di Stokes: il caso delle superfici parametriche
La formula di Stokes dà un’ulteriore relazione che ora collega integrali di curva
nello spazio e integrali di superficie.
Osservazione 244 Abbiamo specificato “curva nello spazio” per intendere
che se in queste considerazioni interviene la normale alla curva, come nell’osservazione 245,
questa va calcolata con la regola con cui si calcola la normale alla curva nello
spazio; ossia, n→(s)
è colineare ed ha lo stesso verso di t→′(s).
E ciò anche se, per caso, la curva che si considera appartiene ad un piano. _
Consideriamo una superficie parametrica Σ
Σ : (u,v) →r→(u,v) = x(u,v)i→ + y(u,v)j→ + z(u,v)k→,(u,v) ∈ Ω.
Supponiamo che la parametrizzazione sia iniettiva e di classe
C2.
Consideriamo una curva semplice e chiusa, con sostegno in
Ω:
γ : t → u(t)i→ + v(t)j→,t ∈ [a,b].
Indichiamo con Ωγ la regione
interna alla curva γ. La
regione Ωγ è contenuta
in Ω e la restrizione
di r→(u,v) alla chiusura di
Ωγ definisce una calotta
che indichiamo con Σ1.
Diciamo che la calotta Σ1
ha per bordo
la curva γ1
parametrizzata da |
t →r→(t) = r→(u(t),v(t))
= x(u(t),v(t))i→ + y(u(t),v(t))j→ + z(u(t),v(t))k→,t ∈ [a,b].
|
La scelta del verso di percorrenza della curva
γ stabilisce un’orientazione
su γ1 mentre la scelta di
considerare i→ come primo
elemento della base di ℝ2
stabilisce un’orientazione sulla normale a
Σ1. Le
due orientazioni non hanno relazioni tra loro: per esempio sia
Σ : r→(u,v) = ui→ + vj→ + 1 − u2 − v2k→.
Le due curve
γ : t →1
2[cos ti→ + sin tj→],γ̃ : t →1
2[sin ti→ + cos tj→],
identificano la medesima calotta, ma le corrispondenti curve
γ1 e
γ̃1
hanno orientazioni opposte. Volendo correlare un’integrale sulla superficie
Σ1 con
l’integrale sul suo bordo, dobbiamo correlare le due orientazioni. Per fissare le
idee, consideriamo assegnata l’orientazione della superficie, ossia il verso
positivo della normale e scegliamo di conseguenza quella sulla curva, ma
niente vieta di fare il contrario e talvolta questo è effettivamente utile.
Definitione 6 Diciamo che l’orientazione della calotta
Σ1
e quella del suo bordo
γ1
sono concordi quando vale la regola d’Ampère: una persona in piedi sulla
superficie nel verso positivo della normale, vede un punto mobile sulla curva
passare dalla sua destra alla sua sinistra. _
Osservazione 245 Facendo tendere ad un punto della curva la posizione
della persona che osserva il moto, si vede che l’orientazione della calotta e quella
del suo bordo sono concordi quando i tre versori della tangente alla curva,
della normale alla curva e della normale alla superficie, presi in quest’ordine,
formano un sistema di riferimento positivo. Supponiamo che un punto P(t)
di γ1
percorra la curva a partire da P(a),
portandosi dietro questo sistema di riferimento. Dato che la parametrizzazione
della superficie è iniettiva, il punto P(t)
torna alla posizione iniziale quando t = b.
E alla fine del giro il sistema di riferimento viene a trovarsi nella posizione che
aveva all’inizio. Ricordiamo che in queste considerazioni n→(s) = t→′(s)∕||t→′(s)||. _
Vale:
Teorema 246 (di Stokes) Valgano le ipotesi dette sopra, in particolare sia iniettiva e di classe
C2 la parametrizzazione
della superficie. Sia γ1
il bordo di Σ1
e Σ1 e
γ1 abbiano orientazioni
compatibili. Sia V →(x,y,z) un campo
vettoriale di classe C1,
definito su Ω.
Vale
|
∫
Σ1rotV → ⋅dΣ → = ∫
γ1V → ⋅dr→.
| (8.35) |
Il calcolo che prova questo teorema è in appendice. Il significato fisico del teorema
di Stokes è il seguente: La circuitazione del campo vettoriale lungo il bordo di
Σ1 è uguale al
flusso attraverso Σ1
del rotore del campo vettoriale stesso. Notiamo che, con le notazioni introdotte per
le forme differenziali, anche il Teorema di Stokes si scrive
Infatti, se ω è
una 1–forma
differenziale i cui coeffcienti sono le componenti del campo vettoriale
V →, è immediato
calcolare che dω
è quella 2–forma
differenziale i cui coeffcienti sono le componenti del rotore di
V →.
Confrontiamo ora le espressioni dei teoremi di Green e di Stokes scritte mediante le
formule differenziali. Si vede che essi si possono ambedue scrivere nella forma
generale (8.36).
Osservazione 247 Si osservi
che nel calcolo l’iniettività della parametrizzazione non si è usata. L’iniettività
si è solo usata per l’interpretazione data nell’Osservazione 245. Dunque, la
formula (8.35) vale senza quest’ipotesi, pur di intendere che l’integrale a destra
sia sostituito da
∫
abV →(x(t),y(t),z(t)) ⋅r→′(t)dt.
Però in tal caso la curva γ
potrebbe essere semplice e la curva γ1
potrebbe non esserlo; e quindi il valore dell’integrale non dipenderebbe soltanto
dagli enti geometrici Σ
e γ1,
ma dalla loro parametrizzazione, ciò che non ha senso fisico. Si veda anche
l’osservazione 248. _
8.5.3 Estensioni
Una prima estensione della formula di Stokes si incontra nel caso in cui
la calotta è delimitata da due curve, come nella figura 8.18 a sinistra.
Procedendo come nel caso piano (paragrafo 8.3.5), ossia operando due tagli
vicini come nella figura a destra, ci si riconduce al caso che abbiamo già
trattato e quindi per una superficie siffatta la formula di Stokes assume
l’aspetto
∫
Σdω = ∫
∂Σω = ∫
γ1ω −∫
γ2ω.
Il segno negativo di fronte al secondo integrale dipende dal fatto che la curva
γ2
va orientata in modo discorde rispetto a quello della superficie,
si veda la figura. In questo caso diremo che il bordo di
Σ è costituito dalle due
curve γ1, orientata in modo
concorde, e γ2, orientata in
modo discorde, rispetto a Σ.
Si estendono facilmente queste considerazioni al caso in cui il bordo è costituito da
più curve. Ricapitolando, abbiamo introdotto la formula di Stokes per superfici
date in forma parametrica. Inoltre, abbiamo esplicitamente supposto che sia possibile
orientare la calotta ed il suo bordo in modo concorde. Il fatto è che ciò talvolta non
può farsi e questo è tanto più importante perchè molto spesso in pratica è
necessario usare il teorema di Stokes nel caso in cui la superficie è ottenuta
“incollando” tanti pezzi di superfici parametriche. Chiameremo calotta composta
una calotta cosìottenuta. Si noti che passando da un pezzo di superficie ad un
altro, la normale può variare in modo discontinuo, si veda la figura 8.19
E’ chiaro dalla figura che
∫
Σdω = ∫
Σ1dω + ∫
Σ2dω
e che la formula di Stokes può applicarsi sia a
Σ1 che a
Σ2; che il
contributo degli integrali sul lato comune si elide e quindi che l’integrale
precedente è uguale alla circuitazione del campo vettoriale sui segmenti
che delimitano la superficie, opportunamente orientati. Indicando con
γ la
curva che ha tali segmenti come sostegno, vale ancora
∫
Σdω = ∫
∂Σω.
La discontinuità della normale non costituisce quindi un problema.
Queste considerazioni sono però soltanto apparentemente semplici.
Per renderci conto delle diffcoltà, applichiamole alle superfici nelle due
figure 8.20. Queste sono superfici regolari, il cui bordo è una curva regolare a
tratti, e quindi l’applicazione della formula di Stokes non presenta problemi.
Modifichiamo ora le superfici come in figura 8.21. E’ ancora ovvio che la
formula di Stokes vale. Ma, modifichiamo ulteriormente le superfici, portando i
segmenti affancati a coincidere. Nel caso della superficie a sinistra, la formula di
Stokes vale ancora, nella forma generalizzata perché ora il bordo è costituito
da due curve. Infatti, gli integrali sui due segmenti si elidono. Invece, tali
integrali si sommano nel caso della superficie a destra e quindi per tale
superficie, che si chiama nastro di Möbius, la formula di Stokes non vale.
Osservazione 248 Si noti che nè il cilindro nè il nastro di Möbius sono
superfici “semplici”, ossia con parametrizzazione iniettiva; ma in un caso la
formula di Stokes vale mentre nell’altro non vale; o meglio, vale la formula
di Stokes nell’accezione dell’Osservazione 247, che semplicemente significa:
contare due volte il contributo dei segmenti che si sovrappongono. Notiamo
però che la posizione dei tali segmenti sul nastro di Möbius è arbitraria:
possiamo fare un taglio nella posizione che vogliamo e applicare il Teorema
di Stokes alla superficie ottenuta. D’altra parte il campo vettoriale cambia
da punto a punto e questo vuol dire che il valore dell’integrale cambia a
seconda della posizione del taglio, ossia a seconda del modo che usiamo per
calcolare l’integrale. Dunque, tale integrale non dipende dalle sole proprietà
geometriche del nastro di Möbius, e non ha alcun significato fisico. _
Si suggerisce di costruire un modello del nastro di Möbius usando una striscia di
carta, e di vedere che il suo bordo consiste di un’unica curva. La circuitazione del
campo vettoriale lungo tale curva non ha alcuna relazione col flusso del rotore
attraverso il nastro. Il nastro di Möbius è una superficie regolare, anche se
con parametrizzazione non iniettiva. Dunque, l’unico punto in cui può
cedere l’argomentazione che porta alla formula di Stokes è il punto in cui si
cerca di orientare la superficie ed il bordo in modo concorde. Infatti, ciò
non può farsi. Per vedere ciò, conviene lavorare col versore normale |
n→(u,v) = N→(u,v)
||N→(u,v)||.
| (8.37) |
Questo versore è ben definito perchè
N→(r→) non
è mai nullo. Dunque,
det r→u(u,v)r→v(u,v)n→(u,v)
non si annulla mai: o è sempre positivo, o è sempre negativo. Con la scelta fatta per
n→(u,v), esso è sempre
positivo. Sia ora γ
una curva chiusa che gira lungo tutto il nastro di Möbius,
γ : t →r→(t)
Sia n→(t) = n→(r→(t)). La
funzione n→(t)
varia con continuità, ma la continuità è un concetto locale: niente dice dei valori
che n→(t)
prende in punti “lontani”. Chiediamoci allora cosa accade di
n→(a) e di
n→(b).
Costruendo un modello del nastro di Möbius, si vede immediatamente
che
n→(a) = −n→(b).
E quindi, non è possibile orientare la curva
γ in
modo concorde alla superficie. Ciò da una parte spiega come mai la formula di
Stokes non vale per il nastro di Möbius e dall’altra conduce alle seguenti
definizioni:
Definitione 7 Sia Σ
una superficie composta. Essa si chiama una varietà se il versore normale
n→(r→),
definito da (8.37), esiste per ogni r→,
ed è funzione continua di r→.
La varietà si dice orientabile se lungo ogni arco chiuso r→(t),
t ∈ [a,b],
si ha
n→(r→(a)) = n→(r→(b)).
La formula di Stokes vale per varietà orientabili, il teorema della divergenza vale in regioni
Ω la cui
frontiera è una varietà orientabile.
Osservazione 249 Le superfici sono state introdotte parametricamente, ma
anche come “superfici di livello” di funzioni F(x,y,z),
si veda il capitolo 5. Se la funzione F(x,y,z)
è di classe C1
e il suo gradiente non si annulla, allora le superfici definite da
F(x,y,z) = c
sono superfici orientabili. _
8.6 Appendici
8.6.1 Appendice: fatti da ricordare
Ricordiamo che:
- se
ω = fdx + gdy + hdz,V = fi→ + gj→ + hk→
i coeffcienti di dω
sono le componenti del rotore di V →,
ossia di ∇∧ V .
- Se
ω = fdydz + gdzdx + hdxdy,V = fi→ + gj→ + hk→
allora
dω = (∇⋅V →)dxdydz = (divV →)dxdydz.
Questi fatti vanno ricordati, insieme alla formula seguente, che si ricava facilmente:
divgradf = ∇⋅ [∇f] = Δf = fxx + fyy + fzz = Δf.
8.6.2 Appendice: osservazioni sulla terminologia
Gli argomenti trattati in questo capitolo vanno sotto il nome di “Analisi
Vettoriale”. I termini usati per indicare i singoli argomenti sono però variabili
da autore ad autore (praticamente solo il termine “Teorema di Stokes”
è usato da tutti nel medesimo modo, quando applicato alle curve nello
spazio). Per esempio, l’integrale di curva di prima specie si chiama anche
integrali curvilineo mentre l’integrale di curva di seconda specie si chiama
anche integrale di linea I due integrali di superficie si chiamano anche,
rispettivamente, integrale superficiale ed integrale di flusso Le varie formule
integrali che abbiamo incontrato hanno nomi variabili: la formula di Green (nel
piano) talvolta si chiama anche formula di Riemann ed è niente altro che la
particolarizzazione a curve piane della formula di Stokes nello spazio. Il Teorema
della divergenza (nello spazio) si chiama anche Teorema di Gauss o formula do
Ostrogradski e talvolta “Formula di Green” ed ha una particolarizzazione
al piano che ancora si chiama “formula di Green”. E’ quindi opportuno
memorizzare il significato fisico dei vari teoremi per saperli identificare in contesti
diversi.
8.7 Appendice: Una dimostrazione del Teorema di Stokes
Dimostriamo il teorema di Stokes in un caso particolare: supponiamo cioè che la
superficie Σ
sia cartesiana, parametrizzata da
Σ : (x,y) → (x,y,z(x,y)).
Però per maggior chiarezza indichiamo con
(u,v) i punti di
Ω; ossia imponiamo
la condizione x = x(u,v) = u,
y = y(u,v) = v. Notiamo che
in questo caso particolare la calotta ed il suo bordo sono orientate in modo concorde quando
la curva γ
è orientata positivamente; ossia quando una punto mobile su
γ vede la regione
interna Ωγ alla sua
sinistra. Sia V →(x,y,z) = f(x,y,z)i→ + g(x,y,z)j→ + h(x,y,z)k→
il campo vettoriale. Nel nostro caso particolare, si ha
∂x
∂u = 1,∂y
∂v = 1,∂x
∂v = 0,∂y
∂u = 0.
Inoltre, fx = fu,
fy = fv ed analoga
notazione per g
ed h.
Dunque si calcola: |
∫
γ1fdx + gdy + hdz = ∫
γ fdu + gdv + h∂z
∂udu + ∂z
∂vdv
= ∫
γfdu + gdv + h(zudu + zvdv) = ∫
γ(f + hzu)du + (g + hzv)dv
= ∫
Ωγd (f + hzu)du + (g + hzv)dv
= ∫
Ωγ ∂
∂u g + hzv − ∂
∂v f + hzu dudv
= ∫
Ωγ (gu + gzzu) − (fv + fzzv) + (huzv − hvzu) dudv.
|
Mostriamo che anche il flusso del rotore è uguale a questo integrale:
|
∫
Σ1rotV → ⋅dΣ → = ∫
Ωγ (hv − gz)(−zu) − (fz − hu)zv + (gu − fv) dudv
= ∫
Ωγ (gu + gzzu) − (fv + fzzv) + (huzv − hvzu) dudv.
|
Ciò prova l’uguaglianza cercata.
Capitolo 9
Campi conservativi
In questo capitolo studieremo l’esistenza del potenziale di un campo vettoriale,
equivalentemente, di una primitiva di una forma differenziale. Cambieremo un po’
le notazioni perché in molte applicazioni il potenziale si indica col simbolo
V . Quindi useremo un altro
simbolo, per esempio F→,
per indicare il campo vettoriale.
9.1 Potenziale
Supponiamo che il campo vettoriale F→(r→)
definito su una regione Ω sia il
gradiente di una funzione
V (r→) di classe
C1. Si sa dalla fisica
che la funzione V
si chiama il potenziale del campo vettoriale e che un campo vettoriale dotato di
potenziale si chiama conservativo. I campi conservativi hanno grande importanza
per le applicazioni.
Si faccia attenzione a non confondersi con i segni: in fisica,
V (r→)
si chiama il potenziale del campo
F→(r→)
mentre −V (r→)
ne è l’energia potenziale In fisica si lavora
più frequentemente con l’energia potenziale di
F→(r→),
ossia con la funzione −V (r→),
talvolta indicata come “energia potenziale
V (r→)”.
In questo caso V (r→)
non è il potenziale di F→(r→)
ma di −F→(r→).
Vogliamo dare condizioni atte a riconoscere se un assegnato campo vettoriale è conservativo
su una regione Ω
e, se lo è, vogliamo calcolarne il potenziale. Per evitare complicazioni
puramente tecniche assumeremo che i campi vettoriali e le funzioni
siano definiti e con la regolarità che verrà richiesta in una regione
Ω ̃ e che la regione
Ω in cui si lavora abbia
chiusura contenuta in Ω ̃.
In questo modo le derivate delle funzioni sono automaticamente continue sia su
Ω che
sulla sua chiusura. Col termine “curva” inoltre intenderemo “curva regolare a
tratti”. Vediamo subito una condizione necessaria che deve essere soddisfatta dai
campi conservativi. Premettiamo quest’osservazione:
Lemma 250 Vale
∮
γF→(r→) ⋅dr→ = 0
per ogni curva chiusa
γ
di sostegno in
Ω
se e solo se
∫
γ1F→(r→) ⋅dr→ = ∫
γ2F→(r→) ⋅dr→
per ogni coppia di curve
γ1
e
γ2
aventi gli stessi estremi.
Dim. Per la dimostrazione, basta notare che se le due curve
γ1 e
γ2 hanno gli stessi
estremi, allora γ1 − γ2
è una curva chiusa, si veda il Lemma 228, e quindi
0 = ∫
γ1−γ2F→(r→) ⋅dr→ = ∫
γ1F→(r→) ⋅dr→ −∫
γ2F→(r→) ⋅dr→.
Noto ciò, proviamo:
Teorema 251 Se
F→(x,y,z)
è un campo conservativo su una regione
Ω
allora
∮
γF→ ⋅dr→ = 0
su ogni curva chiusa di sostegno in Ω.
Equivalentemente,
∫
γF→ ⋅dr→
ha il medesimo valore su tutte le curve γ
di sostegno in Ω,
che hanno i medesimi estremi.
Dim. Calcoliamo l’integrale di F→(r→)
integrale su un arco γ.
Sia
F→(r→) = V x(x,y,z)i→ + V y(x,y,z)j→ + V z(x,y,z)k→.
Si trova |
∫
γV xdx + V ydy + V zdz =
∫
ab[V
x(x(t),y(t),z(t))ẋ(t) + V y(x(t),y(t),z(t))ẏ(t) + V z(x(t),y(t),z(t))ż(t)]dt
= ∫
ab d
dtV (x(t),y(t),z(t)) = V (x(b),y(b),z(b)) − V (x(a),y(a),z(a)).
|
Dunque, in questo caso particolare, l’integrale non dipende dalla curva
γ, ma
solo dai suoi estremi. In particolare è nullo se gli estremi coincidono, ossia se la
curva è chiusa. _ Il teorema precedente non è immediatamente usabile, perché
richiede infinite verifiche; una per ciascuna curva chiusa di sostegno in
Ω.
Ciò può lievemente migliorarsi. Notando che ogni curva di sostegno in
Ω si
può approssimare mediante poligonali, si potrebbe provare:
Lemma 252 Accade che
∮
γF→ ⋅dr→ = 0
per ogni curva
γ
di sostegno in
Ω
se e solo se
∮
P F→ ⋅dr→ = 0
per ogni poligonale P
di sostegno in Ω.
Proviamo ora che le condizioni necessarie appena individuate sono anche suffcienti:
Teorema 253 Un campo vettoriale di classe
C1
F→(r→) = f(r→)i→ + g(r→)j→ + h(r→)k→
ammette potenziale
V (r→)
se e solo
se la sua circuitazione lungo ogni poligonale chiusa e semplice di sostegno in
Ω
è nulla.
Dim. La condizione necessaria si è già provata. Mostriamo che essa
è anche condizione suffciente. Per fissare le idee, supponiamo
r→ ∈ Ω ⊆ ℝ3 e
quindi
F→(r→) = u(x,y,z)i→ + v(x,y,z)j→ + w(x,y,z)k→.
fissiamo un punto r→0
qualsiasi in Ω e costruiamo
una funzione V (r→) in
questo modo: sia Pr→ una
poligonale che congiuge r→0
con r→.
L’integrale
∫
Pr→F→(c→) ⋅dc→
dipende solo dagli estremi della poligonale, ossia dai punti
r→0 e
r→,
dato che l’integrale sulle poligonali chiuse è nullo. Essendo
r→0
fissato, il valore dell’integrale dipende solo dal secondo estremo
r→ della
curva. Dunque la funzione
V (r→) = ∫
Pr→F→(c→) ⋅dc→
è ben definita. Mostriamo che essa è derivabile e che le sue derivate parziali sono le
componenti di F→.
Consideriamo per questo la derivata rispetto ad
x,
V x(x,y,z) = lim hh→0V (x + h,y,z) − V (x,y,z)
h .
Calcoliamo V (x + h,y,z)) percorrendo
prima la curva Pr→,
che congiunge r→0
con r→, e
poi il segmento parametrizzato da
c→1(t) = x + th,c2(t) = y,c3(t) = z,t ∈ [0, 1].
Questo segmento congiunge il punto di coordinate
(x,y,z) col punto di
coordinate (x + h,y,z).
Indichiamo con S
questo segmento, cosìche |
V (r→ + h→) − V (r→) = ∫
γr→F→(c→) ⋅dc→ + ∫
SF→(c→) ⋅dc→ −∫
γr→F→(c→) ⋅dc→
= ∫
SF→(c→) ⋅dc→ = ∫
01[u(x + th,y,z)]hdt.
|
Dunque, (usando il Teorema 139 nel passaggio dalla penultima all’ultima riga)
|
V x(x,y,z) = lim h→0V (x + h,y,z) − V (x,y,z)
h
= lim h→0 1
h ∫
01[u(x + th,y,z)]hdt = lim
h→0 ∫
01u(x + th,y,z)dt
= ∫
01u(x,y,z)dt = u(x,y,z)
|
come si voleva. In modo analogo si trattano le altre derivate. _
Osservazione 254 Ricordiamo che la circuitazione di un campo di forze
lungo una curva chiusa si interpreta come il lavoro che il campo compie su un
punto che percorre la curva. Il teorema precedente mostra quindi che un campo
è conservativo se e solo se esso compie lavoro nullo su ogni punto che percorre una
qualsiasi curva chiusa di sostegno in Ω.
Inoltre:
Teorema 255 Due diversi potenziali del medesimo campo vettoriale, definiti
su una medesima regione Ω,
hanno differenza costante.
Dim. Perchè la loro differenza U(x,y,z) = V 1(x,y,z) − V 2(x,y,z)
ha derivate parziali tutte nulle. Dunque è costante su ogni poligonale e quindi sulla regione
Ω. _ L’uso
del Teorema 253 per verificare se un campo vettoriale è conservativo, richiede infinite
verifiche e quindi non può usarsi per risolvere problemi concreti. Per dare un criterio
utilizzabile in pratica, ricordiamo la nostra ipotesi, che il campo vettoriale sia di classe
C1. Quindi il potenziale,
se esiste, è di classe C2
e quindi il Teorema di Schwarz relativo all’eguaglianza delle derivate miste mostra:
Teorema 256 Se il campo vettoriale
F→(r→) = u(x,y,z)i→ + v(x,y,z)j→ + w(x,y,z)k→
di classe C1
è conservativo, valgono le uguaglianze |
uy = vx,uz = wx,vz = wy
| (9.1) |
in ogni punto di Ω.
Dim. Infatti, sia
F→(x,y,z) = V x(x,y,z)i→ + V y(x,y,z)j→ + V z(x,y,z)k→
Ossia, per esempio, u = V x,
v = V y. Il
Teorema di Schwarz mostra che
uy = V x,y = V y,x = vx.
Le altre uguaglianze si ottengono in modo analogo. _
Osservazione 257 Le condizioni (9.1) sono state scritte per campi vettoriali su
ℝ3,
ma naturalmente valgono anche per campi vettoriali in
ℝ2. Se
n = 2
queste condizioni si riducono a
Le condizioni (9.1) sono le condizioni per avere
rotF→(r→) = ∇∧F→(r→) = 0.
Un campo vettoriale il cui rotore è nullo si dice irrotazionale Il Teorema 256 si
riformula quindi come segue:
Teorema 258 Ogni campo conservativo è irrotazionale.
L’esempio seguente mostra che il viceversa non vale:
Esempio 259 Si consideri il campo vettoriale su
ℝ2 dato
da |
F→(x,y) = − y
x2 + y2i→ + x
x2 + y2j→.
| (9.3) |
Il campo vettoriale (9.3) è rappresentato nella figura 9.1, a sinistra. Si vede
immediatamente che questo campo vettoriale verifica, ove è definito, le
uguaglianze (9.2); però non è conservativo perchè, calcolando la circuitazione
lungo la circonferenza parametrizzata da
γ : x = r cos t,y = r sin t,t ∈ [0, 2π]
si trova
r2 ∫
γ sin 2t + cos 2tdt = 2r2π≠0.
Dunque, il potenziale non esiste, grazie al Teorema 251. Se si prova
ad usare la costruzione nel Teorema 253, si trova una funzione
V (x,y) che
però non è estendibile con continuità a tutto il piano privato della sola origine:
la funzione che si ottiene non ammette estensione continua ad almeno una semiretta
uscente dall’origine. _
Osservazione 260 Il campo vettoriale (9.3) è il campo di forze prodotto
da un filo percorso da corrente elettrica, in un piano ad esso perpendicolare.
Si sa che tale campo di forza può fornire energia ad una particella che è
vincolata a percorrere una traiettoria circolare centrata sul filo. Questo campo
di forze è rappresentato nella figura 9.1, a sinistra. _
Ricapitolando, abbiamo una condizione necessaria e suffciente perché un campo sia
conservativo, espressa dal Teorema 253. Questo teorema però richiede di
fare infinite verifiche, e non è praticamente usabile. Abbiamo poi una
semplice condizione necessaria, espressa dal Teorema 256. Però l’esempio
precedente mostra che questa condizione non è suffciente. Essa però diviene
suffciente se la regione su cui si lavora ha una semplice proprietà geometrica:
Definitione 8 Una regione
Ω ⊆ ℝ2
si dice semplicemente connessa se vale
Ωγ ⊆ Ω
per ogni curva di Jordan γ
il cui sostegno è in Ω.
Una regione Ω
di ℝ3
si dice semplicemente connessa se due qualsiasi punti di Ω
possono congiungersi con una curva regolare
ed inoltre se ogni curva regolare semplice e chiusa in Ω
è bordo di una superficie parametrica semplice il cui sostegno è contenuto in
Ω. _
Intuitivamente, una regione di ℝ2
è semplicemente connessa quando “non ha buchi”. Una regione di
ℝ3
semplicemente connessa può avere “buchi” che però devono essere “localizzati”.
Per esempio, una corona circolare non è semplicemente connessa in
ℝ2
mentre un guscio sferico è semplicemente connesso in
ℝ3. Invece,
togliendo da ℝ3
un cilindro (illimitato in ambedue le direzioni) la regione rimanente non è
semplicemente connessa. Una classe (molto particolare) di insiemi semplicemente connessi
in ℝ3 è
quella degli insiemi convessi. Proviamo ora:
Teorema 261 Sia F→(r→)
un campo vettoriale di classe C1
su una regione Ω.
Supponiamo che F→(r→)
sia irrotazionale. Se la regione Ω
è semplicemente connessa allora il campo è conservativo.
Dim. Proviamo il teorema in ℝ2.
Per provare che il campo è conservativo, dobbiamo provare che vale
∮
γF→(r→) ⋅dr→ = 0
su ciascuna curva regolare, semplice e chiusa
γ di sostegno
in Ω. Sia
Ωγ la regione interna a
γ. Dato che la regione
Ω è semplicemente
connessa, Ωγ è tutta
contenuta in Ω
e quindi si può usare il Teorema di Green, ossia il Teorema di Stokes sul piano. Si
ha quindi
∫
γF→(r→) ⋅dr→ = ∫
ΩγrotF→(x,y) ⋅k→dxdy = 0
perché il rotore è nullo. La dimostrazione del teorema in
ℝ3 è analoga:
bisogna ricordare che, per ipotesi, ogni curva regolare, semplice e chiusa contenuta
in Ω
è bordo di una calotta parametrica semplice
Σ, tutta contenuta
nella regione Ω,
sulla quale si può usare il teorema di Stokes in
ℝ3. Per il Teorema
di Stokes, detta γ
la poligonale e Σ
la calotta,
vale
∫
γF→ ⋅dr→ = ∫
ΣrotF→ ⋅dΣ → = 0.
L’esistenza del potenziale segue dall’arbitrarietà della
γ, si
veda il Teorema 253. _
Osservazione 262
- Un disco del piano, o una palla in ℝ3,
sono regioni semplicemente connesse. Dunque ogni campo irrotazionale
è localmente conservativo. Diffcoltà possono sorgere solamente se ci si
“allontana troppo” dal punto di partenza.
- Applicando quest’osservazione al campo vettoriale dell’Esempio 259,
possiamo dire che questo campo vettoriale ammette potenziale per
esempio in ogni semipiano o in ogni angolo che non contiene l’origine.
- La condizione sulla regione Ω
è solamente suffciente. Il potenziale di un campo vettoriale (irrotazionale)
può esistere anche in una regione che non è semplicemente connessa,
come mostra l’esempio seguente. Il campo vettoriale è definito su ℝ2 − (0, 0):
F→(x,y) = x
x2 + y2i→ + y
x2 + y2j→.
Questo campo vettoriale ammette potenziale su
ℝ2 − (0, 0),
dato da |
V (x,y) = 1
2 log(x2 + y2).
| (9.4) |
9.1.1 Il calcolo del potenziale
Il Teorema 253 insegna a costruire il potenziale di un campo conservativo: basta calcolarne gli
integrali lungo curve di forma “semplice”, per esempio poligonali che congiungono un punto
r→0 fissato col
generico punto r→
della regione. E’ ovvio perè che questa via è praticamente percorribile solamente
se due punti della regione possono congiungersi con un segmento, in modo da
avere integrali facilmente calcolabili. Il caso più semplice è quello in cui
Ω è una regione stellata
rispetto ad un punto r→0
(si veda la definizione al paragrafo 3.1.1). In questo caso esiste un punto
r→0 che può essere congiunto
al generico punto r→ ∈ Ω
mediante un segmento
t →r→0 + t(r→ −r→0),t ∈ [0, 1].
In tal caso, Dalla dimostrazione del Teorema 253,
V (r→) = ∫
01F→(r→
0 + t[r→ −r→0]) ⋅ [r→ −r→0]dt.
Peró questa non è l’unica costruzione possibile e non è la più semplice
nemmeno nel caso di una regione stellata. Di solito, è più semplice risolvere, con
successivi calcoli di primitive, le equazioni
V x(x,y,z) = u(x,y,z),V y(x,y,z) = v(x,y,z),V z(x,y,z) = w(x,y,z).
Vediamo ciò su un esempio.
Esempio 263 Sia
F→(x,y,z) = r→
|r→|3r→ = xi→ + yj→ + zk→.
In questo caso, |
u(x,y,z) = x
(x2 + y2 + z2)3∕2,
v(x,y,z) = y
(x2 + y2 + z2)3∕2,
w(x,y,z) = z
(x2 + y2 + z2)3∕2.
|
Si noti che la funzione non è definita nell’origine; ma sembra di intuire che su
ogni curva di Jordan regolare che non passa per l’origine si possa appoggiare una
calotta regolare che non incontra l’origine, alla quale applicare il Teorema di Stokes.
Inoltre, si vede facilmente che il campo vettoriale verifica le uguaglianze (9.1). Si
può quindi sperare di costruirne un potenziale in ogni regione semplicemente
connessa che non contiene l’origine. Per questo si noti che integrando rispetto ad
x
l’uguaglianza
V x(x,y,z) = u(x,y,z) = x
(x2 + y2 + z2)3∕2
si trova
V (x,y,z) = − 1
x2 + y2 + z2 + Φ(y,z).
Derivando rispetto ad y
ed uguagliando a v(x,y,z)
si trova
Φy(y,z) = 0
e quindi Φ(y,z) non dipende
dalla variabile y:
Φ(y,z) = Φ(z).
Derivando ora V (x,y,z)
rispetto a z ed
uguagliando a w(x,y,z)
si trova
Φ′(z) = 0
e quindi Φ(z)
viene ad essere costante. il campo vettoriale proposto ammette quindi come
potenziali le funzioni
V (x,y,z) = − 1
x2 + y2 + z2 + c
ove c
è una qualsiasi costante. Si osservi che il campo vettoriale dell’esempio precedente
è quello gravitazionale (cambiato di segno) e che il potenziale trovato è il
potenziale newtoniano (cambiato di segno). La figura 9.1, a destra, mostra la
restrizione del campo vettoriale al piano x = 0. _
Ricordiamo nuovamente che la condizione di irrotazionalità è necessaria per
l’esistenza del potenziale mentre la condizione che la regione sia semplicemente
connessa è solamente suffciente. Un campo irrotazionale potrebbe annettere
potenziale anche su una regione non semplicemente connessa. Il potenziale (9.4)
mostra un caso di questo tipo.
9.2 Il linguaggio delle 1-forme
differenziali
Gli stessi argomenti che abbiamo visto sopra possono riformularsi col linguaggio
delle forme differenziali. In tal caso usa una terminologia un po’ diversa.
Consideriamo il campo vettoriale e la forma differenziale
F→(r→) = f(r→)i→+g(r→)j→+h(r→)k→,ω = f(r→)dx+g(r→)dy+h(r→)dz.
Allora:
Possiamo quindi riformulare i teoremi visti per i campi differenziali in questo modo:
- una 1-forma
differenziale esatta ha integrale nullo su ogni curva chiusa;
- una 1-forma
differenziale esatta è chiusa;
- 1-forma
differenziale chiusa su una regione semplicemente connessa è esatta.
Il linguaggio delle forme differenziali è particolarmente comodo quando si
vuol passare al caso di forme differenziali di ordine superiore, come ora
vediamo.
9.3 Primitive di 2-forme
differenziali
Consideriamo ora una 2-forma
differenziale
ω = fdydz + gdzdx + hdxdy.
In certe applicazioni ha interesse sapere quando esiste una
1-forma
differenziale ω̃
tale che
dω̃ = ω
con ω̃
di classe C2.
Una condizione necessaria è:
dω = d[dω̃] = 0.
Infatti, sia
ω̃ = adx + bdy + cdz.
Allora, come si è visto,
dω̃ = [cy − bz]dydz + [az − cx]dzdx + [bx − ay]dxdy.
Dunque, |
d[dω̃] = [cyx − bzx]dxdydz + [azy − cxy]dydzdx + [bxz − ayz]dzdxdy
= [(azy − ayz) + (bxz − bzx) + (cyz − cxy)]dxdydz
|
e l’ultima espressione è nulla per il Teorema di Schwarz. La condizione
dω = 0 si
scrive esplicitamente |
fx(x,y,z) + gy(x,y,z) + hz(x,y,z) = 0.
| (9.7) |
Una 2-forma
differenziale ω
che verifica
dω = 0
si dice chiusa Se esiste, una 1-forma
differenziale ω̃
per cui
dω̃ = ω
si dice una primitiva di ω;
e una 2-forma
differenziale dotata di primitive si dice ancora esatta Proviamo:
Teorema 264 Una 2-forma
differenziale chiusa su un rettangolo è anche esatta.
Dim. Infatti, supponiamo che la (9.7) valga e mostriamo un modo per costruire la
ω̃. Uguagliando i
coeffcienti di ω e
di ω̃, si vede che
i coeffcienti a(x,y,z),
b(x,y,z) e
c(x,y,z)
devono verificare
Proviamo a vedere se si trova una 1-forma
ω̃ che
verifica queste uguaglianze e che ha nullo uno dei coeffcienti, per esempio il coeffciente
c. In
tal caso, da (9.8) e (9.8) si trova |
a(x,y,z) = c1(x,y) + ∫
z0zg(x,y,s)ds
b(x,y,z) = c2(x,y) −∫
z0zf(x,y,s)ds
|
dove c1(x,y) e
c2(x,y) sono arbitrarie funzioni,
indipendenti da z. E ora
mostriamo che le funzioni c1(x,y)
e c2(x,y) si
possono determinare in modo che valga anche la (9.10). Per ottenere ciò basta |
∂
∂xc2(x,y)−∂
∂yc1(x,y) = Φ(x,y,z) = h(x,y,z)+∫
z0zf
x(x,y,s)ds+∫
z0zg
y(x,y,s)ds.
| (9.11) |
Notiamo che
∂
∂zΦ(x,y,z) = fx(x,y,z) + gy(x,y,z) + hz(x,y,z) = 0
e quindi in realtà
Φ(x,y,z) = Φ(x,y).
Notato ciò, si vede che ci sono infiniti modi per soddisfare (9.11). Un modo è di
scegliere
c1(x,y) = 0,c2(x,y) = ∫
0xΦ(s,y)ds.
9.4 Alcune formule importanti
Nel corso della trattazione precedente, abbiamo visto che tutte le
0-forme, tutte
le 1-forme e
tutte le 2-forme
(di classe C2)
verificano
D’altra parte quest’uguaglianza si verifica facilmente anche per le
3-fome (e anzi,
per le 3-forme si
ha addirittura d[fdxdydz] = 0.
Vogliamo vedere l’aspetto particolare che questa formula assume quando
si vuole scrivere per mezzo degli operatori differenziali. Ricordiamo che:
- se
ω = fdx + gdy + hdz,V = fi→ + gj→ + hk→
i coeffcienti di dω
sono le componenti del rotore di V →,
ossia di ∇∧ V .
- Se
ω = fdydz + gdzdx + hdxdy,V = fi→ + gj→ + hk→
allora
dω = (∇⋅ V )dxdydz.
Dunque, la (9.12) assume la forma: |
rotgradf = ∇∧ [∇f] = 0,
divrotV → = ∇⋅ [∇∧V →] = 0.
|
Queste formule vanno ricordate insieme a quella, già incontrata e facilmente
ricavabile,
divgradf = ∇⋅ [∇f] = Δf = fxx + fyy + fzz.
Capitolo 10
I sistemi di equazioni differenziali
10.1 Introduzione
Ricordiamo dal corso di Analisi matematica 1 che si chiama equazione
differenziale del primo ordine un’equazione che ha per incognita una funzione
x→(t),
generalmente a valori vettori, a cui si richiede di verificare |
x→′(t) = f→(t,x→(t)).
| (10.1) |
Si parla di problema di Cauchy quando si richiede di risolvere l’equazione
differenziale (10.1) insieme all’ulteriore condizione
Convenzionalmente, la variabile t
si chiama tempo, t0
si chiama istante iniziale e la condizione (10.2) si chiamacondizione iniziale o
condizione di Cauchy. Alcune precisazioni vanno richiamate esplicitamente:
- con le lettere in grassetto si intendono vettori e x→
indica un vettore di dimensione n,
n ≥ 1.
Quando n > 1
la (10.1) si chiama anche un sistema di equazioni differenziali.
- Sia x→ ∈ ℝn.
Il dominio dell’equazione differenziale è una regione (quindi un aperto
connesso) di ℝn+1
su cui f→(t,x→)
è definita. Attenzione che il dominio dell’equazione differenziale è
sempre un aperto, anche se f→(t,x→)
è definita su un chiuso più grande, si veda l’esempio 266.
- la funzione incognita x→
è calcolata nel medesimo istante t
ovunque essa compare.
- Per soluzione dell’equazione (10.1) si intende una funzione
x→(t)
tale che:
- x→(t)
è definita su un intervallo (a,b)
e ivi derivabile.
- per ogni t,
la coppia (t,x→(t))
appartiene al dominio dell’equazione differenziale.
- per ogni t ∈ (a,b)
l’uguaglianza (10.1) è verificata.
Si dice che la soluzione x→(t)
verifica il problema di Cauchy (10.1), (10.2) quando
t0 ∈ (a,b) e
x→(t0) = x→0.
- Infine, ricordiamo che, come notazione, generalmente invece di (10.1) si
scrive
x→′ = f→(t,x→)
senza indicare la dipendenza di x→
da t.
Vedremo che, sotto opportune condizioni sulla funzione
f→(t,x→), il problema
di Cauchy (10.1)-(10.2) ammette soluzione unica, definita su un opportuno intervallo aperto
contenente t0.
Scriveremo x→(t; t0,x→0)
per indicare la soluzione del problema di Cauchy. Quando
t0 è sottinteso,
scriveremo x→(t; x→0).
Si noti che le soluzioni di equazioni differenziali, essendo funzioni continue definite
su intervalli, sono curve parametriche. Per chiarire la definizione di soluzione,
consideriamo gli esempi seguenti:
Esempio 265 Sia
x′ = 1 + x2.
Si sa che x(t) = tan t
verifica l’uguaglianza in ogni punto t
in cui la funzione tan t
è definita. Però x(t) = tan t
non è soluzione dell’equazione differenziale perché non è definita su un
intervallo. Invece, la restrizione di tan t
all’intervallo (−π∕2,π∕2)
è soluzione, cosìcome è soluzione la restrizione di tan t
all’intervallo (π∕2, 3π∕2).
Consideriamo ora la funzione tan(t + π∕4).
Questa funzione è soluzione dell’equazione differenziale, sull’intervallo (−3π∕4,π∕4).
Dunque, soluzioni diverse della medesima equazione differenziale possono avere
domini DIVERSI; e in generale una soluzione è definita soltanto su un “piccolo”
intervallo. _
Inoltre:
Esempio 266 Sia
x′ = 1 − x2,x(0) = 0.
Il dominio della funzione f(t,x) = f(x) = 1 − x2
è l’insieme chiuso ℝ × [−1, 1].
Questo però non può essere il dominio dell’equazione differenziale perché,
per definizione, il dominio dell’equazione differenziale deve essere un aperto.
Scegliamo allora come dominio dell’equazione differenziale l’insieme aperto
ℝ × (−1, 1).
Procedendo per separazione di variabili, si trova che la soluzione è
x(t) = sin t
definita su (−π∕2,π∕2).
Infatti, per t →±π∕2
la soluzione tende rispettivamente a −1
e +1.
In questi punti, 1 − x2
è definita, ma i punti (−π∕2,−1)
e (π∕2, 1)
non appartengono al dominio dell’equazione differenziale. Dunque, per t →±π∕2,
il grafico (t,x(t))
della soluzione “esce” dal dominio dell’equazione differenziale. _
Chiediamoci ora perché è cosìimportante insistere sul fatto che una soluzione deve
rimanere all’interno dell’insieme su cui il secondo membro dell’equazione è definito.
La ragione è questa: nei due esempi precedenti la soluzione si trova esplicitamente
procedendo per separazione di variabili, ma in pratica la soluzione di un’equazione
differenziale deve calcolarsi numericamente. Consideriamo per esempio la soluzione
x(t) = sin t
dell’equazione nell’esempio 266. Se si vuol ridefinire il concetto di
soluzione in modo da accettare che la soluzione sia definita anche in
−π∕2 e
π∕2 allora la soluzione viene
ad essere definita su ℝ.
Però, nessun metodo numerico riuscirà a trovare tale soluzione perché quando
t = π∕2 errori
comunque piccoli fanno uscire dal dominio e bloccano l’algoritmo numerico usato per trovare
la soluzione, qualunque esso sia. Come si è visto nel corso di Analisi Matematica 1,
si chiama equazione differenziale del secondo ordine un’equazione nell’incognita
x(t) del
tipo
x″(t) = f(t,x(t),x′(t))
usualmente scritta senza indicare la dipendenza da
t,
x″ = f(t,x,x′).
Si noti che non abbiamo usato lettere in grassetto perché in generale studieremo
le equazioni di ordine superiore per incognite scalari (anche se niente vieta di
studiare sistemi di equazioni di ordine superiore, si veda l’Esempio 269). Il
problema di Cauchy si ottiene ora associando all’equazione differenziale le ulteriori
condizioni
x(t0) = x0,x′(t
0) = x1
ossia ricercando soluzioni dell’equazione differenziale che hanno assegnata posizione e
velocità in un medesimo istante. E’ noto dal corso di Analisi Matematica 1 che un’equazione
di ordine n
è |
x(n) = f(t,x,x′,…,x(n−1)).
| (10.3) |
Il problema di Cauchy corrispondente si ottiene fissando un punto
t0 e
richiedendo che in questo punto la soluzione cercata verifichi le condizioni
x(t0) = x0,x′(t
0) = x1,…,x(n−1)(t
0) = xn−1.
E’ importante notare che ogni equazione differenziale di ordine
n può scriversi
come sistema di n
equazioni differenziali. La (10.3) può scriversi in forma di sistema come segue: si scriva
x1(t) invece di
x(t) e quindi si
definiscono x2(t),
…, xn(t)
dalle uguaglianze |
ẋ1(t) = x2(t)
ẋ2(t) = x3(t) ⋮
ẋn(t) = f(t,x1(t),x2(t),…,xn−1(t)).
| (10.4) |
Osservazione 267 Si noti l’uso intercambiabile dell’apostrofo e del punto per
indicare la derivata rispetto al tempo t.
Mostriamo ora due esempi. Abbiamo detto che ogni equazione differenziale di ordine
n
può scriversi come sistema. Invece, il viceversa non vale: esistono sistemi di
n
equazioni differenziali che non corrispondono ad equazioni differenziali di ordine
n.
Esempio 268 Si consideri il sistema di equazioni differenziali
Le sue soluzioni sono x(t) = etx
0,
y(t) = ety
0. In
particolare, la (10.5) è risolta da |
x(t) = et,y(t) = 2et.
| (10.6) |
Si vede subito che nessuna equazione scalare del secondo ordine
scritta in forma di sistema del primo ordine, ossia scritta come
x′ = y,y′ = f(x,y)
può avere le medesime soluzioni di (10.5). Infatti la prima uguaglianza
x′ = y
non vale se
x(t)
ed
y(t)
sono le funzioni in (10.6). _
Esempio 269 Si considerino due punti materiali di massa M1
ed M2
vincolati a scorrere (senza attrito) su un segmento orizzontale. Il punto M1
è attaccato ad una molla (di costante elastica k1)
a sua volta fissata nell’origine ed il punto M2
è collegato al punto M1
attraverso una seconda molla di costante elastica k2.
Indichiamo con x
ed y
rispettivamente l’ascissa del primo e del secondo punto. Allora, le equazioni di
Newton per questo sistema sono
M1x″ = −k1x + k2(y − x)
M2y″ = −k2(y − x).
Si ha quindi un sistema di due equazioni del secondo ordine. Questo può
rappresentarsi come sistema di quattro equazioni del primo ordine,
x1′ = 1
M1x2
x2′ = −k
1x1 + k2(y1 − x1)
y1′ = 1
M2y2
y2′ = −k
2(y1 − x1).
La fisica insegna che la posizione e velocità “iniziali”, ossia assegnate ad
un certo istante di tempo, e le forze cui il sistema è soggetto, determinano
l’evoluzione futura del sistema. Dunque, se vogliamo un primo controllo che
il modello matematico che abbiamo costruito effettivamente corrisponda alle
proprietà fisiche del sistema, dovremo verificare che l’evoluzione nel tempo
delle funzioni x(t),
x′(t),
y(t),
y′(t)
sia univocamente determinata dalla conoscenza delle costanti M1,
M2,
k1,
k2
e dei quattro numeri x(t0),
x′(t
0),
y(t0),
y′(t
0).
A questo quesito risponde il Teorema di Cauchy, Teorema 270. _
I sistemi di equazioni differenziali considerati negli esempi precedenti sono tutti sistemi
lineari, ossia hanno forma
x→′ = Ax→ + f→
con A matrice (generalmente
dipendente dal tempo, A = A(t))
ed f→ = f→(t) dipendente
dal solo tempo t
e non da x→ (anzi,
negli esempi, f→ = 0).
Quando f→ = 0
il sistema si dice lineare omogeneo, altrimenti si chiama affne. La funzione
f→(t) si
chiama termine noto. Sono invece esempi di sistemi non lineari i seguenti
x′ = −x(a + by),y′ = −y(cx + d)
che si incontra in problemi di dinamica di popolazioni (equazione di Lotka-Volterra)
oppure
x″+ax′+cx+𝜖x3 = cos ωt,ossia x′ = y
y′ = −ay − cx − 𝜖x3 + cos ωt
(equazione di Duffn) che si incontra nello studio delle oscillazioni elastiche. Un
altro esempio importante di equazione differenziale non lineare è l’equazione di
van der Pol
x″ = −x + μ(x2 − 1)x′
che si incontra nello studio di certi circuiti elettrici. Consideriamo ora un
caso particolare: supponiamo che l’equazione differenziale (10.1) abbia
forma
x→′ = f→(x→)
con f→ che non
dipende da t. In
questo caso si dice che il sistema è autonomo o tempo invariante. Esso descrive fenomeni
la cui legge fisica è costante nel tempo e le sue soluzioni hanno una proprietà importante:
sia x→(t) una
soluzione e sia y→(t) = x→(t + τ)
con τ
numero fissato ma qualsiasi. Allora,
y→′(t) = x→′(t + τ) = f→(x→(t + τ)) = f→(y→(t)),
ossia y→(t)
è ancora soluzione. Si osservi che ciò non avviene se
f→ dipende
anche da t
perché in questo caso si trova
y→′(t) = f→(t + τ,y→(t))
che è una diversa equazione differenziale. La funzione
t →y→(t) = x→(t + τ) è
una curva ottenuta riparametrizzando (in modo molto semplice) la curva
t →x→(t). Per
questa ragione, quando si studiano sistemi autonomi, conviene studiare sia il grafico
(t,x→(t)) della soluzione sia la
“curva soluzione” t →x→(t).
Nel contesto dei sistemi autonomi questa si chiama orbita Graficamente
se ne rappresenta il sostegno, ossia l’immagine della funzione e, quando
serve, si indica anche il verso di percorrenza al crescere del tempo
t. Un punto
x→0 per cui
f(x→0) = 0 è detto
punto di equilibrio o stazionario (talvolta si dice anche soluzione stazionaria.) In tal caso,
x→(t) ≡x→0 è soluzione
costante di (10.1). Se l’equazione differenziale è autonoma, l’orbita di tale soluzione si riduce
al punto x→0
stesso. Un punto critico si dice isolato se in un suo intorno non vi sono altri punti
critici.
Concludiamo dicendo che le equazioni differenziali che stiamo studiando si
dicono “ordinarie” in opposizione alle “equazioni differenziali a derivate parziali”
che si incontrano quando l’incognita dipende da più variabili e quindi le derivate
che compaiono nell’equazione sono derivate parziali. Come esempio di equazione a
derivate parziali si consideri
∂
∂tx + ∂
∂sx = 0
e si provi che tutte le funzioni
x(t,s) = ϕ(t − s)
con ϕ di
classe C1
risolvono quest’equazione.
10.2 Esistenza e unicità di soluzione
Consideriamo il problema di Cauchy |
x→′ = f→(t,x→),x→(t
0) = x→0.
| (10.8) |
Come si è notato all’esempio 269, vanno conosciute condizioni che assicurino la
risolubilità di questo problema, e condizioni che implichino l’unicità della soluzione.
Ricordiamo che per definizione la soluzione deve essere definita in un intervallo che
contiene t0
al suo interno. E’ suffciente però mostrare che la soluzione esiste in
[t0,t0 + a)
perché lo stesso argomento si potrà poi applicare all’intervallo
(t0 − a,t0].
Inoltre, proveremo l’esistenza di soluzioni in un opportuno
intervallo, non necessariamente il più grande possibile. Se
x→(t) risolve (10.8) allora
x→(t) è una curva parametrica
che nel punto x→(t0)
ha per tangente la retta di parametrizzazione |
x→(t) = x→(t0) + f→(t0,x→(t0))(t − t0).
| (10.9) |
Ciò suggerisce di costruire come approssimazione della soluzione una spezzata
costituita da segmenti delle rette di forma (10.9). Bisogna però usare un po’ di
cautela, perché si sa già che in generale una soluzione di (10.8) può solo
definirsi in un “piccolo” intervallo, si ricordi l’Esempio 265. Il teorema che si può
provare è il seguente:
Teorema 270 (di Cauchy) Sia
x→ = (x1,…,xn)
e supponiamo che la funzione
f→(t,x→)
e le sue derivate parziali rispetto alle componenti di
x→
siano continue in una regione
D
contenente il “rettangolo”
R
R = {(t,x→)|t0 − a ≤ t ≤ t0 + a,||x −x0||≤ b}.
Il problema di Cauchy (10.8) ammette soluzione unica su un intervallo
(t0 − T,t0 + T)
ove T
dipende sia da t0
che da x0.
La dimostrazione del teorema è piuttosto tecnica, ma è opportuno accennare all’idea
che guida la dimostrazione, perché questa suggerisce un modo importante di
pensare alle equazioni differenziali. Costruiamo una successione di funzioni
x→(N)(t), continue su
[t0,t0 + T], che, si può provare,
converge a una funzione x→(t)
che risolve (10.8). Per questo, dividiamo l’intervallo
[t0,t0 + T] in
N parti
uguali mediante i punti
t0,t0 + δ,t0 + 2δ,…,t0 + (N − 1)δ,ove δ = T∕N.
Inizialmente siamo nel punto (t0,x→0).
Definiamo la funzione x→(N)(t)
sul primo intervallo [t0,t0 + δ]
indicandone il grafico: il grafico è il segmento di retta
y = x→(t0) + f→(t0,x→(t0))(t − t0),t ∈ [t0,t0 + δ].
In questo modo si identifica in particolare
x→(N)(t
0 + δ). A partire dal punto
(t0 + δ,x→(N)(t
0 + δ)) si ripeta il procedimento:
si definisca x→(N)(t)
per t ∈ [t0 + δ,t0 + 2δ]:
x→(N)(t) = x→(N)(t
0+δ)+f→(t0+δ,x→(N)(t
0+δ))(t−(t0+δ)),t ∈ [t0+δ,t0+2δ].
Si ripeta quindi questo procedimento fino a coprire tutto l’intervallo
[t0,t0 + T]. In generale
avremo, per k = 0, 1,…,N − 1,
x→(N)(t) = x→(N)(t
0+kδ)+f→(t0+kδ,x→(N)(t
0+kδ))(t−(t0+kδ)),t ∈ [t0+kδ,t0+(k+1)δ].
La figura 10.1 illustra questo procedimento.
In questo modo, per ogni N,
si costruisce una spezzata che si chiama spezzata di Eulero. Si può provare che la successione di funzioni
x(N)(t) converge uniformemente
ad una funzione x(t)
sull’intervallo (t0 − T,t0 + T),
purché T
sia opportunamente scelto. Ora, vorremmo sostituire questa funzione nei due membri
di (10.8) trovando che i due membri differiscono per un errore che tende a zero per
N → +∞.
Però, questo non può farsi perché le funzioni
x(N)(t) non sono
derivabili; e anche se si potesse fare a poco servirebbe perché la sola convergenza
uniforme niente permette di concludere sulla derivata della funzione limite
x(t). Viene
però in aiuto un’altra idea: integrando i due membri dell’equazione differenziale in (10.8)
si vede che x→(t)
risolve (10.8) se e solo se essa risolve l’equazione integrale |
x→(t) = x→0 + ∫
t0tf→(s,x→(s))ds.
| (10.10) |
E’ possibile sostituire la x(N)(t)
nei due membri dell’equazione integrale, e stimare lo scarto tra i due membri, provando che esso
tende a zero per N → +∞;
e usando la sola convergenza uniforme è ora possibile completare la dimostrazione
del teorema. Omettiamo i dettagli della dimostrazione, contentandoci di avere
illustrato queste idee fondamentali. _ La dimostrazione del Teorema di Cauchy
suggerisce un modo importante di pensare ad un’equazione differenziale, che illustriamo
nel caso del sistema
x′ = f(x,y),y′ = g(x,y) :
si può pensare al campo vettoriale f(x,y)i→ + g(x,y)j→
come ad un “campo di velocità” che trasporta un pallino inizialmente nella posizione
(x0,y0). La
traiettoria descritta dal pallino è la soluzione del problema di Cauchy con quel dato
iniziale. Da questo punto di vista,
il vettoref→(x→) = f(x,y) g(x, y)
applicato inx→ = x y
rappresenta la velocità che il pallino ha se transita dalla posizione
x→ all’istante
t.
Le isocline
Consideriamo il caso di un sistema autonomo di due equazioni differenziali
x′ = f(x,y),y′ = g(x,y).
La dimostrazione del Teorema di Cauchy suggerisce di considerare il luogo dei punti che vengono
incontrati dalle soluzioni dell’equazione differenziale con pendenza assegnata. Escludendo i punti nei
quali sia f
che g
si annullano, le orbite sono curve regolari di parametrizzazione
(x(t),y(t)). Per fissare le idee, sia
x′(t0)≠0. La pendenza della
tangente nell’istante t0
è
y′(t0)
x′(t0) = g(x(t0),y(t0))
f(x(t0),y(t0)).
Se invece x′(t0) = 0 allora
la tangente è verticale. Dunque, le orbite hanno tangente verticale nei punti dell’insieme identificato da
f(x,y) = 0; hanno tangente
con pendenza m
nei punti dell’insieme identificato da
g(x,y)
f(x,y) = m.
Quest’insieme si chiama l’isoclina di pendenza
m. L’isoclina di
pendenza m
ha questa proprietà: le soluzioni escono dai suoi punti con tangenti tutte parallele, con la medesima
pendenza m.
Se si riescono a disegnare “molte” isocline e quindi a disegnare su di esse segmenti di pendenza
m, si
può pensare di tracciare una soluzione del problema di Cauchy in questo modo: si parte dal dato
(x0,y0),
che appartiene ad una certa isoclina, corrispondente alla pendenza
m0. Si traccia per
(x0,y0) un segmento
parallelo a y = m0x
fino ad incontrare la “successiva” isoclina (successiva, tra quelle tracciate) diciamo corrispondente alla
pendenza m1.
Dal punto di intersezione si fa uscire un segmento parallelo a
y = m1x fino ad
incontrare l’isoclina successiva, ecc. Si costruisce una spezzata che approssima la soluzione del
problema di Cauchy.
10.2.1 Equazioni differenziali lineari a coeffcienti costanti
Si è visto, al paragrafo 2.4.4 che l’equazione differenziale lineare a coeffcienti
costanti |
x→̇ = Ax→ + f→(t)
| (10.11) |
(con A
matrice n × n)
ha per soluzioni le funzioni
x→(t) = eAtx→
0 + ∫
0teA(t−s)f→(s)ds.
Il membro destro di questa formula si chiama soluzione generale o anche integrale
generale della (10.11). La soluzione generale della (10.11) si ottiene sommando ad
una soluzione particolare,
∫
0teA(t−s)f→(s)ds
tutte le funzioni
eAtx→
0,x→0 ∈ ℝn.
Al variare di x→0
queste sono tutte le soluzioni dell’equazione lineare omogenea
associata, ossia dell’equazione che si ottiene dalla (10.11) ponendo
f→(t) = 0.
Dunque, il calcolo dell’integrale generale si riduce al calcolo dell’esponenziale di
matrici
eAt.
Il calcolo di quest’esponenziale è tutt’altro che semplice in generale e
ci limitiamo a studiare il caso dei “sistemi piani”, ossia il caso in cui
x→ ∈ ℝ2.
Consideriamo prima di tutto l’equazione lineare omogenea, ossia assumiamo
f→(t) = 0. Dobbiamo
ricordare alcune proprietà delle matrici, che richiamiamo esclusivamente nel caso di
matrici 2 × 2.
Proprietà analoghe valgono in generale, ma la casistica diventa
sempre più complessa all’aumentare delle dimensioni della matrice.
Ogni matrice ammette almeno un autovalore ossia almeno un numero
λ tale
che
det[A − λI] = 0.
Questo discende dal teorema fondamentale dell’algebra, perché
det[A − λI] è un
polinomio non costante, e quindi ammette almeno uno zero che però può essere un
numero complesso, anche se gli elementi della matrice sono reali. Il polinomio
det[A − λI] si chiama polinomio
caratteristico della matrice A.
In corrispondenza di ciascun autovalore, si trovano soluzioni
v→ non
nulle dell’equazione lineare
Av→ = λv→.
Questi vettori non nulli si chiamano gli autovettori relativi all’autovalore
λ. Naturalmente, se
v→ è un autovettore
relativo a λ,
anche i suoi multipli lo sono. Dobbiamo osservare che:
- se λ
è un numero complesso, anche i suoi autovettori sono autovettori a
elementi complessi; ossia, implicitamente anche se gli elementi della matrice
A
sono reali, ci riconduciamo a lavorare con vettori ad elementi complessi;
- autovettori relativi ad autovalori diversi sono linearmente indipendenti.
Consideriamo la funzione
x→(t) = eAtv→,.
Allora,
d
dteAtv→ = AeAtv→
è una soluzione della (10.11) (anche se
v→ non è
autovettore di A).
Se
Av→ = λv→,
si ha
eAtv→ = ∑
n=0+∞An
n! v→ = ∑
n=0+∞Anv→
n! = ∑
n=0+∞λnv→
n!
ossia
eAtv→ = eλtv→.
Dunque, noto un autovalore λ
e un suo autovettore v→,
è facile scrivere alcune soluzioni dell’equazione lineare omogenea: sono le
funzioni
αeλtv→
con α
coeffciente qualsiasi (in generale, coeffciente complesso). Esista ora un secondo
autovalore μ
e sia w→
un suo autovettore. Allora, anche le funzioni
βeμtw→
risolvono l’equazione ldifferenziale lineare omogenea
e quindi anche le funzioni
la risolvono. Quanto detto fin’ora vale per sistemi di qualunque
dimensione. Supponiamo ora che il sistema sia di dimensione
2. Dato che
i vettori v→
e w→
sono linearmente indipendenti, ogni vettore a due dimensioni
x→ si
può rappresentare in modo unico come
x→ = αv→ + βw→;
Ossia, al variare dei coeffcienti α
e β, le
funzioni (10.13) permettono di esprimere tutte le soluzioni di (10.12). Dunque, la (10.13)
è la soluzione generale di (10.12). Si noti che il fatto importante è l’esistenza di due
autovettori v→
e w→
linearmente indipendenti: le considerazioni precedenti possono ripetersi anche se i due
autovettori v→
e w→
corrispondono ad un medesimo autovalore, ossia se
λ = μ. Sfortunatamente, non
è vero che ogni matrice 2 × 2
debba avere due autovettori linearmente indipendente, come mostra l’esempio
seguente:
Esempio 271 Gli autovettori della matrice
01 0 0
sono tutti i multipli di
v→ = 1 0 :
Questa matrice non ha due autovettori linearmente indipendenti. _
In tal caso, si procede come segue: si identifica (l’unico) autovettore
λ ed un suo autovettore
v→. Ricordiamo che
per definizione v→≠0.
Quindi si considera l’equazione
A − λIw→ = v→.
E’ un fatto che, se A,
matrice 2 × 2,
non ha due autovettori linearmente indipendenti, quest’equazione ammette soluzione
w→, e inoltre
w→ è linearmente
indipendente da v→.
Identificati v→
e w→,
si costruiscono due polinomi, a valori vettori, uno di grado
0 ed uno
di grado 1:
p→0 = v→,p→1 = v→t + w→.
Nel caso che stiamo ora considerando, si verifica facilmente per sostituzione che la
soluzione generale di (10.12) è |
eλt αp→
0 + βp→1(t) .
| (10.14) |
Abbiamo quindi scritto la soluzione generale di (10.12) in ciascuno dei casi che
possono presentarsi: in tutti i casi la soluzione generale è combinazione lineare di
due soluzioni fondamentali. Delle soluzioni
eλtp→
0,eλtp→
1(t)
delle soluzioni
eτtv→,eμtw→
(con λ = μ oppure
λ≠μ) quando
la matrice A
ammette due autovettori linearmente indipendenti. Queste coppie di soluzioni di (10.12)
si chiamano un sistema fondamentale di soluzioni. Rimane da chiarire un punto: se la
matrice A
è reale ma ammette due autovalori complessi e coniugati, le soluzioni scritte sopra
prendono valori complessi. Vorremmo trovare un diverso sistema fondamentale di
soluzioni, che però prendano valori reali.
Il caso degli autovettori complessi e coniugati Le considerazioni precedenti valgono
per ogni matrice A
sia che i suoi autovalori siano reali sia che siano complessi. Se però la matrice
2 × 2 ha elementi reali
ed un autovalore λ
complesso, allora anche λ̄
è autovalore; e quindi siamo automaticamente nel caso in cui la matrice ha due
diversi autovalori e quindi due autovettori linearmente indipendenti: la soluzione
generale di (10.12) è data da (10.13). Siano
λ± = ξ ± iω
gli autovalori e sia v→+ = v→1 + iv→2
un autovettore di λ+. In
quest’espressione, v→1
e v→2
sono vettori reali, che però non sono essi stessi autovettori di
A. E’
un fatto che
v→̄+ → = v→1 − iv→2
è un autovettore di λ−.
Usando la (10.13) si vede quindi che un sistema fondamentale di soluzioni è |
eξt e−iωt v→
1 + iv→2
= eξt v→
1 cos ωt −v→2 sin ωt + i v→2 cos ωt + v→1 sin ωt
eξt e−iωt v→
1 − iv→2
= eξt v→
1 cos ωt −v→2 sin ωt − i v→2 cos ωt + v→1 sin ωt.
| (10.15) |
Queste soluzioni prendono valori complessi. Sommandole e sottraendole (e dividendo
rispettivamente per 2
e per 2i)
si trovano due soluzioni a valori reali:
eξt v→
1 cos ωt −v→2 sin ωt,eξt v→
1 cos ωt + v→2 sin ωt.
Questo anche è un sistema fondamentale di soluzioni, a valori reali. Infatti,
combinandole linearmente si ritrovano le (10.15) e quindi ogni altra soluzione
di (10.12).
10.2.2 Il caso dell’equazione completa e delle equazioni di ordine superiore
Limitandoci ancora al caso di sistemi di due equazioni, mostriamo un metodo
per risolvere l’equazione completa. Abbiamo bisogno di un risultato di
algebra lineare, che è questo: scriviamo esplicitamente il sistema in forma |
x′ =ax + by + f
1
y′ =cx + dy + f
2
| (10.16) |
e consideriamo la matrice
A = ab c d .
Mostriamo:
Teorema 272 Esiste una matrice
P
(generalmente ad elementi complessi) tale che
det P≠0
e inoltre tale che
PAP−1 = P ab
cd P−1 = αβ
0δ .
Dim. Bisogna ricordare che ogni matrice ammette almeno un autovalore ed un
corrispondente autovettore, che in generale sono complessi. Dunque si trovano
v→ e
α tali
che
Av→ = αv→.
Sia w→ un qualsiasi
vettore indipendente da v→
e consideriamo la matrice
P−1 = v→w→ .
Questa matrice trasforma gli elementi della base canonica ordinatamente in
v→ e
w→. La sua inversa quindi
trasforma ordinatamente v→
e w→ nella
base canonica. E’:
AP−1 = αv→z→ z→ = Aw→ = βv→+δw→
e quindi
PAP−1 = αβ
0δ .
Sia ora
g→(t) = g1(t)
g2(t) = Pf→(t) = P f1(t)
f2(t)
Applicando la trasformazione P
al sistema, questo si riduce a
ξ′ = αξ + βη + g
1(t),η′ = δη + g
2(t).
La seconda equazione è un’equazione nella sola incognita
η(t), che si sa
risolvere; nota η(t),
questa funzione si sostituisce nella prima equazione, ottenendo un’equazione nella sola incognita
ξ, che ancora si sa risolvere.
Calcolate le funzioni ξ(t)
ed η(t), la
soluzione x→(t)
si ottiene come
x→(t) = P−1 ξ(t)
η(t) .
Quando il termine noto ha forma “particolare”, dal corso di Analisi Matematica 1,
si sa che conviene ricercare una soluzione di forma “particolare”. Consideriamo
quest’esempio:
x′ = αx + βy + eγt,y′ = δy + eσt.
La risoluzione di questo sistema può farsi semplicemente con le tecniche viste nel corso
di Analisi Matematica 1 e quindi non entriamo nei dettagli del calcolo. Notiamo però
che se δ≠σ
allora le soluzioni della seconda equazione hanno forma
aeδt + beσt.
Se però δ = σ
allora le soluzioni sono
aeδt + bteδt.
Inserite queste nella prima equazione, la soluzione della prima equazione ha forma
rispettivamente
ceαt + aeδt + beσtoppureceαt + aeδt + bteδt
se α è diverso
dagli esponenti che si sono incontrati risolvendo la seconda equazione; altrimenti compariranno
fattori tn
con n > 1.
Si esaminino i vari casi e si ritrovi che i possibili valori di
n sono
0,
1 e
2. E
ora consideramo il caso di un sistema omogeneo di tre equazioni differenziali lineari.
Anche in questo caso esistono trasformazioni di coordinate che “triangolarizzano” il
sistema, ossia lo riducono a forma
x′ =αx+βy+χz
y′ = δy+σz
z′ = γz
Anche questo sistema si risolve a partire dall’ultima equazione e, risoltala, si vede
che z(t) = aeγt.
Sostituita queste funzione nelle prime due equazioni, ci si riconduce al
caso di due equazioni lineari con termine affne visto sopra. E quindi
nell’espressione delle prime due componenti compariranno termini della forma
tneγt con
n = 0,
n = 1 oppure
n = 2.
10.2.3 Il comportamento in futuro delle soluzioni
Spesso interessa conoscere il comportamento delle soluzioni di un sistema di equazioni
differenziali per t → +∞.
Quando si fa questo studio, si dice che si studia il “comportamento in futuro” delle
soluzioni. Facciamo questo studio nel caso dei sistemi lineari omogenei
di due equazioni differenziali. In tal caso, le soluzioni sono funzioni
x→(t) con
x→(t) vettore a due
componenti x(t)
ed y(t).
Dunque le soluzioni rappresentano curve parametriche piane. Per questo, i sistemi
due due equazioni differenziali si chiamano anche sistemi piani ed il piano
(x,y) si chiama
piano delle fasi Vogliamo descrive le soluzioni di un sistema lineare omogeneo piano
sul piano delle fasi e vedere come il comportamento dipenda dagli autovalori della
matrice A
e, se c’è un solo autovalore, anche dal fatto che esistano due autovettori
linearmente indipendenti, o uno solo. La soluzione stazionaria
x→(t) = 0 → esiste
sempre. Noi considereremo solamente il caso in cui
ker A = 0 →
ossia in cui il sistema differenziale ammette un’unica soluzione stazionaria, e questa
è x→(t) = 0 →.
Interessa conoscere il comportamente delle altre soluzioni rispetto alla soluzione
stazionaria. Questo comportamento viene descritto introducendo opportune
definizioni.
Nel caso lineare però non abbiamo bisogno dei dettagli di queste
definizioni. Diciamo per ora che interessa sapere se tutte le soluzioni
rimangono limitate e se tutte le soluzioni tendono a zero per
t → +∞.
Naturalmente tutte le soluzioni rimangono limitate se le due soluzioni che costituiscono
un sistema fondamentale di soluzioni sono ambedue limitate; tutte le soluzioni tendono a
zero per t → +∞
se ciò accade per ambedue gli elementi di un sistema fondamentale di
soluzioni. Ricapitoliamo i casi che si possono presentare: casi: 1) la matrice
A ha due autovettori
indipendenti v1
e v2,
corrispondenti rispettivamente agli autovalori reali
λ1 e
λ2 (non
necessariamente distinti). Allora un sistema fondamentale di soluzioni è dato
da
x1(t) = eλ1tv
1,x2(t) = eλ2tv
2;
2) la matrice A ha due
autovettori complessi coniugati v ± iw
e corrispondenti rispettivamente agli autovalori complessi coniugati
α ± iβ . Un
sistema fondamentale di soluzioni è dato da
x1(t) = eαt(cos(βt)v − sin(βt)w),x
2(t) = eαt(cos(βt)w + sin(βt)v);
3) la matrice A ha
un solo autovalore λ
ma non vi sono due autovettori indipendenti. Allora, detto
v1 un autovettore, si
risolve il sistema
(A − λI)v2 = v1 e un
sistema fondamentale di soluzioni è dato da
x1(t) = eλtv
1,x2(t) = eλt(tv
1 + v2).
Esaminando separatamente questi tre casi, si vede che valgono i risultati elencati
nella tabella 10.1.
Tabella 10.1: Comportamento asintotico delle soluzioni dei sistemi lineari
piani
Due autovettori linearm. indipendenti
Soluzioni limitate in futuro se e solo se ambedue gli autovalori hanno parte reale non positiva
Due autovettori linearm. indipendenti
Le soluzioni tendono a zero pert→ +∞ se e solo se
integrale di curva di seconda specie
integrale di linea; integrale di linea di seconda specie.
I casi che possono presentarsi sono ben rappresentati negli esempi seguenti.
Esempio 273
- il caso di due autovalori reali distinti e di segno concorde. In questo caso
le soluzioni del sistema diagonalizzato hanno forma
x(t) = eλtx
0,y(t) = eμty
0.
Le orbite sono le curve
yλ = cxμ
percorse verso l’origine se gli autovalori sono negativi, allontanandosi
dall’origine altrimenti. Se λ = μ
le orbite sono rette. Questo caso è illustrato dalla figura 10.2 a sinistra.
Questa configurazione di orbite si chiama nodo.
- I due autovalori sono reali, di segno opposto. In questo caso le soluzioni
sono della forma
x(t) = eλtx
0,y(t) = e−μty
0
con, per esempio, λ > 0
e μ > 0.
Nel caso λ = μ
le orbite sono le iperboli
xy = cost.
e per questa ragione il punto di equilibrio
(0, 0)
si dice di tipo iperbolico, o di sella. La figura (10.2) a destra illustra
questo caso.
- I due autovalori sono puramente immaginari, e coniugati. In questo caso le
soluzioni hanno forma
x(t) = A cos(ωt + ϕ),y(t) = A sin(ωt + ϕ).
Le orbite sono le circonferenze
x2 + y2 = A2.
Il caso è illustrato nella figura 10.3 a sinistra, e il punto di equilibrio
si chiama ora centro.
- I due valori sono numeri complessi e coniugati, ma non puramente
immaginari. In questo caso le soluzioni hanno forma
x(t) = Aeat cos(ωt + ϕ),y(t) = Aeat sin(ωt + ϕ).
In coordinate polari sono descritte da
r(t) = Aeat,𝜃(t) = ωt + ϕ
e sono quindi spirali che si avvolgono verso l’origine se
a < 0,
altrimenti si allontanano dall’origine. Il punto d’equilibrio
(0, 0) è
ora detto fuoco. Questo caso è illustrato nella figura 10.3, a destra. Il numero
a
è la parte reale comune ai due autovalori.
10.3 La stabilità
Consideriamo ora il sistema non lineare
autonomo
Per semplicità supponiamo che tutte le soluzioni di (10.17) siano definite su
[0, +∞).
Ricordiamo che i punti di equilibrio sono quei punti
x→0 tali
che f→(x→0) = 0 →. I
punti di equilibrio corrispondono a soluzioni costanti e spesso queste sono le
“più importanti” tra le soluzioni dell’equazione differenziale. Per questa
ragione, interessa sapere come si comportano soluzioni il cui dato iniziale poco
differisce da un punto di equilibrio; in particolare interessa sapere se per
t → +∞ tali
soluzioni tendono o meno al punto di equilibrio stesso. Introduciamo le definizioni
seguenti.
Definitione 9 Diciamo che tutte le soluzioni di (10.17) sono limitate in
futuro quando per ogni
x→0
esiste
Mx→0
tale che
||x→(t; x→0)|| < Mx→0∀t > 0.
In modo analogo si definisce la limitatezza in passato. Si dice che le soluzioni
di (10.17) sono limitate quando sono limitate sia in futuro che in passato. _
Esempio 274 Consideriamo l’equazione scalare
x′ = ax,
le cui soluzioni sono x(t) = ceat.
Tutte le soluzioni sono limitate in futuro ma non in passato se a < 0;
sono limitate in passato ma non in futuro se a > 0;
sono limitate se a = 0. _
Presentiamo ora le definizioni di stabilità, con riferimento ad un punto di equilibrio
y→0.
Definitione 10 Diciamo che il punto di equilibrio
y→0 è
- stabile quando per ogni 𝜖 > 0
esiste σ > 0
tale che se ||x→0 −y→0|| < σ
allora ||x→(t; x→0) −y→0|| < 𝜖
per ogni t > 0
(si noti: σ ≤ 𝜖).
- attrattivo se esiste σ > 0
tale che se ||x→0 −y→0|| < σ
allora lim t→+∞||x→(t; x→0)|| = y→0.
L’insieme dei vettori x→0
tali che lim t→+∞||x→(t; x→0)|| = y→0
si chiama il bacino d’attrazione di y→0.
- asintoticamente stabile se è sia stabile che attrattivo.
Osservazione 275 E’ bene notare che l’attrattività non implica la stabilità. _
Si potrebbe pensare che se y→0
è un punto di equilibrio stabile allora si possa sempre scegliere
δ = 𝜖.
L’esempio seguente mostra che questa congettura è falsa:
Esempio 276 Si consideri il sistema
x′ = 2y,y′ = −x.
L’unico punto di equilibrio è y→0 = (0, 0).
Derivando la prima equazione si vede che
x″ = −2x
e questa è l’equazione del moto armonico. Dunque, le soluzioni del sistema
sono
x(t) = A cos 2t + ϕ,y(t) = − A
2 sin(2t + ϕ).
Dunque le soluzioni descrivono l’ellisse
x2 + 2y2 = 1.
Sono tutte limitate e inoltre se si assegna
𝜖
si può trovare un
δ
tale che
||(x0,y0)|| < δ⇒||(x(t),y(t))|| < 𝜖.
Però, δ
va scelto strettamente minore di 𝜖,
si veda la figura 10.4. _
Quest’esempio verrà nuovamente esaminato in seguito. Osserviamo che se il punto di
equilibrio y→0
è stabile allora le soluzioni (con dato iniziale suffcientemente vicino a
y→0)
sono limitate in futuro e addirittura in modo uniforme: se
||x→0 −y→0|| < δ allora
||x→(t; x→0)|| < 𝜖 + ||y→0|| = Mx→0. In questo
caso Mx→0 = 𝜖 + ||y→0||è
indipendente da x→0
(se ||x→0 −y→0|| < δ).
Il viceversa non vale:
Esempio 277 Consideriamo il sistema descritto in coordinate polari da
r′ = r(1 − r),𝜃′ = 1.
r(t) = 1
è una soluzione costante e, procedendo per separazione di variabili,
log r(t)
|1 − r(t)| = t + c
(si ricordi che r ≥ 0).
Dunque, le soluzioni sono
𝜃(t) = t+h,r(t) = ket
1+ketcon k > 0 se 0 ≤ r(0) < 1
1 se r(0) = 1
ket
ket−1con k > 1 se r(0) > 1.
Le soluzioni descrivono delle spirali che si
avvolgono intorno alla circonferenza di raggio
1.
Tutte le soluzioni sono limitate ma scegliendo
un intorno dell’origine di raggio minore di
1,
non si riesce a rimanere in quest’intorno scegliendo di partire “vicini”
all’origine. Si veda la figura 10.5. _
Concludiamo notando che i risultati della tabella 10.1, che si riferisce
ai sistemi lineari piani autonomi, possono riformularsi con la
terminologia della stabilità. Si ottiene cosìla tabella 10.2, nella quale
y→0 = 0.
Tabella 10.2: La stabilità dei sistemi lineari piani
Due autovettori
linearm. indipendenti
Soluzione nulla stabile se e solo se
ambedue gli autovalori hanno parte reale non positiva
Due autovettori
linearm. indipendenti
Soluzione nulla asintoticamente stabile
se e solo se ambedue gli autovalori hanno parte reale negativa
Autovettori tutti linearmente dipendenti
(e quindi un solo autovalore δ)
Soluzione nulla asintoticamente stabile
se e solo se l’unico autovalore è negativo
Si pone ora il problema di sapere quando un punto di equilibrio di un sistema
piano è stabile oppure asintoticamente stabile. Questo è generalmente un
problema piuttosto diffcile. I due test più semplici che possono usarsi
sono il Teorema di Lagrange, per la stabilità, e il teorema sulla stabilità
“in prima approssimazione”, per la stabilità asintotica. Per chiarire il
significato del Teorema di Lagrange, conviene introdurre la nozione di integrale
primo, che ha un’importanza fondamentale in tutte le applicazioni della
matematica.
10.4 Sistemi piani ed integrali primi
Il concetto di integrale primo non è limitato ai sistemi piani, ma è in questo caso
particolare che noi lo studieremo. Consideriamo quindi il sistema piano |
x′ = f(x,y),y′ = g(x,y).
| (10.18) |
Si chiama integrale primo una funzione
V (x,y) di
classe C1
tale che:
- gli zeri di ∇V (x,y)
sono isolati;
- ogni orbita di (10.18) è contenuta in una curva di livello di V (x,y).
Integrali primi possono non esistere, ma se esistono non sono mai unici: se
V (x,y) è un integrale
primo, anche cV (x,y)
e V (x,y) + c
(con c
costante) lo sono. E’ un fatto che molto spesso quando un integrale primo si può
trovare allora questo dà informazioni importanti sul comportamento delle soluzioni
dell’equazione differenziale. Per esempio:
- se si riesce a trovare un integrale primo allora le orbite del sistema (10.18)
si possono (almeno localmente) calcolare risolvendo l’equazione (non
differenziale) V (x,y) = c.
Grazie al Teorema della funzione implicita, ciò è lecito nell’intorno dei
punti nei quali il gradiente di V (x,y)
non si annulla.
- Se le curve di livello di un integrale primo sono tutte limitate, allora le
soluzioni dell’equazione rimangono limitate al trascorrere del tempo.
Gli integrali primi hanno una relazione importante con le proprietà dei campi
vettoriali. Provando il Teorema di Cauchy, abbiamo visto che al sistema (10.18)
conviene associare il campo vettoriale
F→(x,y) = f(x,y)i→ + g(x,y)j→.
Associamogli anche il campo vettoriale
G→(x,y) = −g(x,y)i→ + f(x,y)j→
ortogonale a F→(x,y) in ogni
punto. Supponiamo che G→(x,y)
ammetta potenziale V (x,y).
Allora, lungo le soluzioni di (10.18) si ha:
d
dtV (x(t),y(t)) = V xx′ + V
yy′ = −gf + fg = 0.
Ossia, V
è un integrale primo di (10.18). Condizione necessaria per l’esistenza del potenziale
V (x,y) del
campo G→(x,y)
è che
−gy = fx
Dunque:
Teorema 278 Supponiamo che il dominio del sistema piano sia una regione
di Jordan. Se
divF→(x,y) = 0
allora il sistema piano ammette integrali primi.
Ovviamente, esistono sistemi che non ammettono integrali primi. Esistono però anche
sistemi che ammettono integrali primi e che non soddisfano alle condizioni del
Teorema 278, che dà una condizione solo suffciente per l’esistenza di integrali
primi:
Esempio 279 Si consideri il sistema piano
t′ = 1,x′ = x.
Chiaramente, la condizione del Teorema 278 non è soddisfatta, ma integrali
primi esistono:
V (t,x) = xe−t
è infatti un integrale primo. _
Ciò nonostante, il caso descritto nel Teorema 278 è particolarmente importante per le applicazioni.
Indicando con H(x,y) un
integrale primo, si ha ∇H = − gf ,
ossia
f = Hy,g = −Hx
e quindi il sistema piano (10.18) si rappresenta come
x′ = H
y,y′ = −H
x.
Sistemi di questa forma si chiamano sistemi hamiltoniani e l’integrale primo
H(x,y) si
chiama l’ hamiltoniana del sistema. Un caso molto importante nel quale è facile
trovare un integrale primo si ha quando si studia |
x″ = −ϕ(x)ossia x′ =y
y′ = − ϕ(x)
| (10.19) |
Si noti che ϕ dipende
dalla sola posizione x
e non dalla velocità y.
Assumiamo ϕ(x) ∈ C1(ℝ).
In questo caso
F→(x,y) = yi→ − ϕ(x)j→
ha divergenza nulla e quindi il sistema è hamiltoniano. Calcolando il potenziale
di
G→(x,y) = ϕ(x)i→ + yj→
si trova l’integrale primo
V (x,y) = 1
2y2 + Φ(x),Φ(x) = ∫
0xϕ(s)ds.
Nelle applicazioni fisiche, il sistema si incontra generalmente scritto nella
forma
mx″ = −ϕ(x)
ove m
è la massa. In tal caso
F→(x,y) = yi→ − 1
mϕ(x)j→,G→(x,y) = 1
mϕ(x)i→ + yj→
ed un integrale primo è
V (x,y) = 1
mΦ(x) + 1
2y2.
Si è detto che i multipli di un integrale primo sono ancora integrali primi. Il
particolare multiplo
E(x,y) = 1
2my2 + Φ(x)
si chiama energia totaledel sistema, mentre si chiamano
rispettivamente energia cinetica ed energia potenziale le due funzioni
my2∕2 e
Φ(x). I
sistemi della forma (10.19) si dicono conservativi, poiché l’energia totale (che è
un integrale primo) rimane costante lungo ogni orbita (in generale ha valore diverso
su orbite diverse):
Teorema 280 L’energia totale “si conserva” (ossia rimane costante) sulle
traiettorie di un sistema conservativo.
Esempio 281 Consideriamo l’equazione
mx″ = −l
g sin x
che rappresenta le oscillazioni di un pendolo di lunghezza costante.
La sua energia totale è
E(x,y) = 1
2my2 + l
g∫
0x sin sds = 1
2my2 − l
g cos x − 1 .
I potenziali sono sempre definiti a meno di una costante additiva, ed usa
scegliere come energia totale la funzione
E(x,y) = 1
2my2 − l
g cos x.
10.4.1 Integrali primi e stabilità
Se si possono studiare le curve di livello di un integrale primo è possibile ottenere
informazioni sulla stabilità di un punto di equilibrio. Mostriamo questo su un
esempio.
Esempio 282 Si consideri il sistema
x′ = 2y,y′ = −x.
E’ immediato notare che
V (x,y) = x2 + 2y2
è un integrale primo di questo sistema. Le curve di livello sono le ellissi
x2 + 2y2 = c.
Usiamo questo per mostrare che l’origine è
un punto di equilibrio stabile. Si fissi per questo
𝜖 > 0
e sia c
cosìpiccolo che l’ellisse x2 + 2y2 = c
sia contenuta nel disco di centro l’origine e raggio
𝜖.
Indichiamo con E
quest’ellisse. Sia δ > 0
cosìpiccolo che la circonferenza di centro l’origine e raggio
δ
sia contenuta nell’ellisse E,
si veda la figura 10.6.
Sia (x0,y0)
un dato iniziale di norma minore di δ.
L’orbita che lo contiene è contenuta in un ellisse che appartiene alla regione
interna all’ellisse E
e quindi in particolare nell’intorno dell’origine di raggio 𝜖.
Ciò mostra la stabilità. _
In generale lo studio geometrico delle curve di livello non è facile. Vogliamo dare un
risultato di stabilità che usi l’idea dell’esempio precedente, ma che non richieda la
determinazione esplicita delle curve di livello. Questo risultato si applica a sistemi
della forma |
mx′ = y,y′ = −ϕ(x)ossiamx″ = −ϕ(x)con ϕ(0) = 0.
| (10.20) |
L’origine, ossia il punto di coordinate
(0, 0), è
punto d’equilibrio di questo sistema. Si sa che a questo sistema si può associare sia
l’energia potenziale
Φ(x),Φ(x) = −∫
0xϕ(s)ds
sia l’“energia” totale
E(x,y) = 1
2my2 + Φ(x).
Diciamo che Φ(x) ha
minimo stretto in 0
quando
Φ(0) < Φ(x)∀x≠0.
Analoga definizione per l’energia totale
E(x,y). Vale:
Teorema 283 (di Lagrange) Supponiamo che 0
sia uno zero isolato di ϕ(x).
Se 0
è punto di minimo stretto per Φ(x)
allora il punto d’equilibrio (0, 0)
del sistema (10.20) è stabile.
Dim. Il fatto che Φ(x)
abbia un minimo stretto in zero implica che l’energia totale
E(x,y) ha minimo
stretto in (0,0):
0 = E(0,0) < E(x,y)∀(x,y)≠(0,0).
Inoltre, l’energia totale è una funzione continua. fissiamo
𝜖 > 0 e
consideriamo il numero
E0 = min{E(x,y),||(x,y)|| = 𝜖}.
Essendo (0,0) un minimo
stretto, segue che E0 > 0.
Scegliamo ora σ > 0
tale che se ||(x,y)|| < σ
allora si abbia
E(x,y) < E0∕2.
Sia (x0,y0) un dato
iniziale con ||(x0,y0)|| < σ.
Sia (x(t),y(t)) la
soluzione corrispondente a tale dato iniziale. Lungo questa soluzione l’energia si conserva e
quindi
E(x(t),y(t)) = E(x0,y0) < E0∕2.
Dunque, ||(x(t),y(t))|| non può mai
prendere il valore 𝜖: se ciò
avvenisse per un valore t̄
di t avremmo
infatti E(x(t̄),y(t̄)) > E0∕2. Quindi,
essendo t →||(x(t),y(t))||
una funzione continua, si ha sempre
||(x(t),y(t))|| < 𝜖.
Ossia, se il dato iniziale ha norma minore di
σ,
in ogni istante successivo la soluzione ha norma minore di
𝜖. L’arbitrarietà di
𝜖 prova che il punto di
equilibrio (0,0) è stabile. _
Dalla definizione di Φ(x)
si vede immediatamente:
Corollario 284 Le condizioni del Teorema 283 sono soddisfatte se la
funzione
ϕ(x)
verifica
xϕ(x) > 0.
Esempio 285 Consideriamo l’equazione
x″ = − sin x
che descrive il moto di un pendolo. Le
condizioni del Corollario 284 sono soddisfatte e quindi il punto di equilibrio
(0, 0)
è stabile. L’energia totale è
E(x,y) = 1
2y2 + cos x.
Alcune delle sue curve di livello intorno al punto d’equilibrio
(0, 0)
sono riportate nella figura 10.7. Dato che l’energia si conserva, una
soluzione che ha dato iniziale all’interno della curva di livello chiusa non
esce dalla regione delimitata da questa curva, in accordo con l’asserto
del Teorema di Lagrange. Se però il dato iniziale è “lontano” da
(0, 0)
allora la traiettoria del sistema ad esso corrispondente si allontana dal punto
di equilibrio. _
10.4.2 Stabilità asintotica e perturbazioni
E’ importante osservare che il teorema di Lagrange dipende da una proprietà di
minimo che non si conserva sotto l’azione di piccole perturbazioni. E in effetti
piccole perturbazioni possono distruggere la proprietà di stabilità, come
mostrano gli esempi seguenti.
Esempio 286 Consideriamo il sistema scalare
x′ = 𝜖x.
Se 𝜖 = 0
allora il punto d’equilibrio 0
è stabile, mentre è instabile per ogni 𝜖 > 0.
Questo esempio non verifica le ipotesi del teorema di Lagrange. Per trovare
invece un esempio che verifica le ipotesi del teorema di Lagrange, consideriamo
x″ = 𝜖x′− x.
Se 𝜖 = 0
questa è l’equazione del moto armonico e verifica le ipotesi del Teorema di
Lagrange. Dunque, (0, 0)
è punto d’equilibrio stabile come d’altra parte si verifica anche direttamente
notando che la matrice corrispondente ha i due autovalori ±i,
distinti e puramente immaginari. Il punto d’equilibrio (0, 0)
diviene instabile per ogni 𝜖 > 0. _
Esempio 287 Consideriamo ora il sistema
x′ = −y − x5,y′ = x − y3.
Questo sistema non ammette integrali primi. Però, se
(x(t),y(t))
è una soluzione,
d
dt x(t) y(t)
2 = −2x6(t)−2y4(t) < 0.
Ciò mostra che la norma decresce e che quindi il punto di equilibrio (0, 0)
è stabile. Si può provare che è addirittura asintoticamente stabile. Però, la
“piccola” perturbazione che consiste nel trascurare i termini x5
ed y3,
che è una perturbazione infinitesima di ordine superiore al primo (rispetto ad
(x,y)),
ne distrugge la stabilità asintotica. _
Invece, la stabilità asintotica dei sistemi lineari si conserva sotto l’azione di “piccole”
perturbazioni. Questa è una proprietà importantissima per le applicazioni, ed
anche molto comoda in pratica perché dà un test facile da usare. Enunciamo il
risultato senza provarlo:
Teorema 288 Sia |
x→′ = Ax→ + f→(x→)
| (10.21) |
e supponiamo che f→(0 →) = 0 →.
Supponiamo inoltre:
Sotto queste condizioni il punto d’equilibrio
0 → è
asintoticamente stabile per il sistema (10.21).
Il teorema precedente può anche essere precisato: si può provare che se la matrice
A ha
un autovalore con parte reale positiva allora l’origine non è stabile per il
sistema (10.21). Questo teorema in pratica si usa come segue: si ha un sistema della
forma |
x→′ = g→(x→),cong→(0 →) = 0 →.
| (10.22) |
Dato che g→(0) = 0, lo
sviluppo di McLaurin di g→
arrestato al primo ordine dà
g→(x→) = Ax→ + f→(x→),A = Jg→(0 →)
e si sa che f→(x→) è infinitesimo
di ordine maggiore di 1
rispetto a ||x→||,
ossia
lim x→→0f→(x→)
||x→|| = 0 →.
Se gli autovalori di A
hanno tutti parte reale negativa, allora il punto d’equilibrio
0 del
sistema (10.22) è asintoticamente stabile.
Si usa dire che il sistema lineare
x→′ = Ax→
si ottiene linearizzando in 0
il sistema x→′ = g(x→).
Quando si usa questo teorema per studiare la stabilità asintotica di un punto
di equilibrio, si dice che si studia la stabilità in prima approssimazione.
|