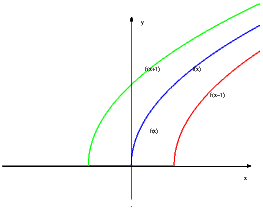
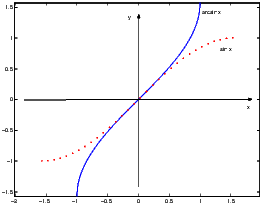
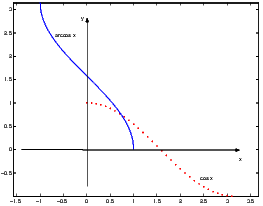
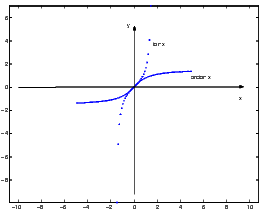
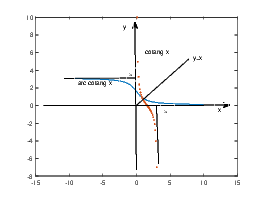
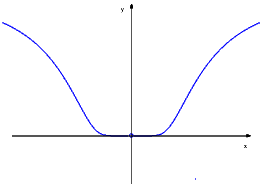
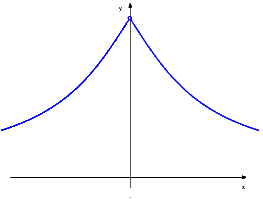
lim nn = 1
2.2 La continuità
Abbiamo bisogno della definizione seguente:
Definizione 70 Sia .
Si dice che
è punto isolato di
quando esiste in intorno
tale che .
Dunque, ogni punto isolato di
è un punto di
e inoltre un punto non può essere contemporaneamente isolato e di accumulazione per
. Per
esempio,
è punto isolato (e quindi non di accumulazione) di
. Veniamo ora
alla definizione di continuità. Per poter parlare di continuità di una funzione in un punto
è necessario che
appartenga al dominio
della funzione.
Sia quindi
una funzione il cui dominio contiene un punto
.
Definizione 71 la funzione
è continua in
quando si verifica uno dei due casi seguenti:
- il punto
è punto isolato di .
- il punto
è punto di accumulazione per ,
esiste
ed inoltre
Si dice che è continua da destra
in quando è
continua la funzione .
Analoga definizione per la continuità da sinistra
Osservazione 72 La scelta di definire “continua” una funzione nei punti
isolati del dominio può sembrare bizzarra. Ne vedremo tra poco l’utilità.
Notiamo però subito una conseguenza: ogni successione è continua in ciascun
punto del suo dominio.
La definizione di continuità può darsi in modo “unificato” come segue:
è continua
in
quando
Questa sembra la definizione di limite, ma
non è così: non abbiamo richiesto che
sia punto di accumulazione di ;
e, se
è punto isolato, l’unico punto di
che verifica
è, per
abbastanza piccolo, il solo punto .
Notare che la definizione di limite richiede anche di imporre
,
condizione che nel contesto della definizione
di continuità si può omettere perché
è automaticamente minore di ,
che è positivo. Dunque, se
è punto di accumulazione di
allora
è continua in
se e solo se
Vale il teorema seguente:
Teorema 73 Siano e
due funzioni continue
in . Le funzioni seguenti
sono continue in :
Se , è continua
in anche
la funzione .
Dim. Esaminiamo il caso della somma: se
è punto isolato per il
dominio di allora questa
funzione è continua in .
Altrimenti, è punto di
accumulazione per il dominio
e per la restrizione a sia
della prima funzione
che di .
Dunque i teoremi sui limiti mostrano che
Osservazione 74 Si noti che può darsi che
sia punto di accumulazione sia di
che di
ma non del dominio della somma. Si consideri l’esempio
Ambedue le funzioni sono continue in ,
con
punto di accumulazione dei domini, ma la funzione somma
è definita nel solo punto .
Se non si definisce “continua” una funzione nei punti isolati del dominio, non
si può affermare che la somma di funzioni continue è continua. Questa è la
ragione per cui abbiamo dato la definizione 71.
In modo analogo si provano anche i risultati seguenti:
Teorema 75 Sia .
La funzione
è continua in
se e solo se è continua sia da destra che da sinistra in .
Teorema 76 (limitatezza locale e permanenza del segno) Se
è continua
in
allora:
Dim. La funzione
è continua in
quando per ogni
esiste tale che
ogni , incluso
il punto ,
si ha
L’asserto relativo alla limitatezza locale segue scegliedo, per esempio,
.
L’asserto relativo alla permanenza del segno si ottiene (quando
) scegliendo per esempio
. con questa scelta, si
trova un intorno di
su cui vale : il
numero cercato è
.
Osservazione 77 Si noti la differenza di quest’enunciato da quello del
teorema relativo ai limiti di funzioni, che potrebbero essere discontinue in
.
Se
non è continua in ,
la conoscenza del limite niente permette di concludere sul segno di .
Infine:
Definizione 78 Una funzione continua in ciascun punto di un insieme
si dice “continua su ”.
Se ,
la funzione si dice “continua sul suo dominio” o anche semplicemente
“continua”. Per dire che
è continua su un insieme
si scrive
o talvolta .
2.2.1 Classificazione delle discontinuità
Sia definita
in , ma non
continua. Il punto
si dice:
Il termine “discontinuità eliminabile” (o discontinuità rimuovibile) si
spiega da solo: cambiando la definizione della funzione nel solo punto
, e
ridefinendo
si trova una funzione continua.
Non si esclude che uno dei due limiti possa coincidere col valore della funzione; ossia
che la funzione sia continua o da destra o da sinistra.
- ogni altro caso di discontinuità si chiama
discontinuità di seconda specie
Infine, consideriamo una funzione
che non è definita in .
Supponiamo però che esista finito
In questo caso, la funzione
è continua: è l’unica estensione per continuità di
ad
.
Osservazione 79 Se
è un punto di accumulazione per ,
l’estensione per continuità di
ad
se esite è unica, ma possono esitere estensioni per continuità non uniche ad
insiemi più grandi. Per esempio
La funzione
ammette infinite estensioni continue ad ,
ma tutte assumono il valore
in .
Se si vuole l’estensione continua a
questa è unica.
2.2.2 Continuità di alcune funzioni importanti
Sono continue le funzioni della lista seguente, ovviamente nei punti in cui sono
definite:
- i polinomi;
- le potenze
con
reale qualsiasi;
- le funzioni razionali;
- la funzione ;
- le funzioni goniometriche:
,
,
e ;
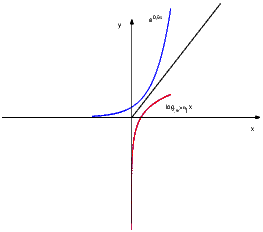
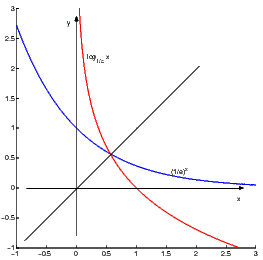
- la funzione logaritmo, ,
per ogni base
(positiva e diversa da );
- la funzione esponenziale
per ogni base .
Vediamo in particolare come si tratta il caso delle funzioni goniometriche.
Limiti e continuità di funzioni goniometriche
Ricordiamo che gli angoli si misurano in radianti, ossia che la
misura dell’angolo al centro di una circonferenza di raggio
è uguale
alla lunghezza dell’arco che l’angolo identifica sulla circonferenza. Proviamo
che per :
- si ha: ;
- si ha: .
Le funzioni ,
e
sono dispari e quindi basta provare le disuguaglianze per
. La figura 2.4 illustra
la definizione di e
: la circonferenza ha
raggio e l’angolo al
centro ha misura ,
ossia
è la lunghezza dell’arco che congiunge i punti
ad
, disegnato rosso. In tal
caso, è la lunghezza
del segmento ,
disegnato rosso e è la
lunghezza del segmento ,
disegnato fucsia.
Si sa che in una circonferenza un arco è più lungo del segmento che ne congiunge gli estremi: l’arco
che congiunge ed
è più lungo del
segmento , ossia
dividendo per
|
| (2.10) |
Il settore circolare è
contenuto nel triangolo rettangolo
e quindi ha area più piccola. Calcolando le aree si trova
ossia, |
| (2.11) |
Conseguenza di queste disuguaglianze: la funzione
è continua
per .
Infatti, il teorema del confronto applicato a
mostra che
Combinando questo con le formule di prostaferesi |
|
segue che le funzioni
e
sono continue. Infatti per sempio si ha
e, per il teorema del confronto, .
In particolare, |
| (2.12) |
Dunque anche le funzioni
e
sono continue. Proviamo ora che
La funzione
è pari e quindi basta calcolarne il limite destro per
tendente
a .
Le disuguaglianze (2.10) e (2.11) implicano (ricordiamo che si lavora per
)
Dividendo per
si trova
Usando (2.12), il teorema di confronto implica che
2.3 Limiti di funzioni composte
Siano e
due funzioni
tali che
cosìche si può calcolare la funzione composta
.
Supponiamo inoltre che sia |
| (2.13) |
Ci si può chiedere se sia vero che |
| (2.14) |
La risposta è in generale negativa. E’ positiva se si impongono ulteriori
condizioni. Vale infatti:
Teorema 80 Sia
punto di accumulazione per il dominio della funzione composta .
Sia
e valga
Supponiamo inoltre che valga una delle tre condizioni seguenti:
-
sia continua (e quindi definita) in ;
-
non prenda il valore ;
- la funzione
non sia definita il .
Allora si ha
Osservazione 81 Il teorema precedente vale anche se
e vale anche se uno o ambedue i limiti
e
sono .
Se però
allora la condizione che
non prenda il valore
non può eliminarsi. Infatti, senza questa condizione può essere che il limite
della funzione composta esista ma diverso da quello di
oppure che non esista, come provano i due esempi seguenti. In ambedue gli
esempi,
Consideriamo ora i due esempi:
Esempio 1) sia .
La funzione
è
Per ogni
si ha
In quest’esempio, il limite della funzione composta esiste, diverso da quello di
.
Esempio 2) E’ ancora
ma la funzione
è
La funzione è
priva di limite per .
Infatti, il limite non può essere nè positivo nè negativo per il teorema di
permanenza del segno, dato che la funzione si annulla in ogni intorno di
(infatti si annulla quando
). E però il limite non può
essere perchè la funzione
prende valore in ogni intorno di
.
Corollario importante del teorema 80 è:
Corollario 82 Una funzione composta di funzioni continue è continua.
Quando è continua
nel punto ,
l’asserto del teorema 80, ossia
può scriversi |
| (2.15) |
Ossia, se è continua
in , il simbolo di
si scambia col simbolo
della funzione .
L’esempio seguente mostra che l’uguaglianza (2.15) è falsa se la funzione
non è
continua in .
Esempio 3) Sia
(la parte intera di )
e sia . Si consideri
il limite per . In
un intorno di si
ha che prende
valore tra ed
, ed il valore
viene assunto
solamente per .
Inoltre
Dunque, per in
un intorno di ,
escluso ,
Di conseguenza,
Illustriamo ora l’uso di questi risultati, che è sia “in positivo”, per garantire la
continuità e l’esistenza di limiti, che “in negativo”, per verificare che certi limiti
non esistono.
2.3.1 Le sottosuccessioni e i loro limiti
Sia una successione
e sia una successione
a valori nei numeri naturali. In questo caso è possibile considerare la funzione composta
, che è ancora una
successione, di indice .
“Successioni composte” definite in modo cosígenerale hanno poco interesse. E’
invece importante il caso in cui la successione
In questo caso la successione composta si chiama sottosuccessione di
(si dice anche che è una “successione estratta” da
) e si
indica col simbolo
Il teorema delle funzioni composte implica che:
Teorema 83 Se
allora si ha anche
per ogni sottosuccessione di .
Osserviamo che si potrebbe anche far vedere che vale il viceversa: si ha
se e solo
se per ogni
sottosuccessione di .
2.3.2 Risultati “in positivo”: calcolo di limiti per sostituzione
Come si è detto, la funzione composta di funzioni continue è continua. Quindi sono
funzioni continue in ciascun punto del loro dominio per esempio le funzioni della tabella 2.5
(nella quale
e
indicano generici polinomi).
Table 2.5: Esempi di funzioni composte
Le funzioni della tabella sono solo alcuni degli esempi di funzioni la
cui continuità segue immediatamente usando il Corollario 82. La tabella
va letta in questo modo. Consideriamo per esempio la prima funzione,
sin log ax. La
funzione
log ax è definita per
x > 0 e prende valori
nel dominio di sin y.
Dunque la funzione composta è definita per ogni
x > 0. Sia
log ax che
sin y sono funzioni
continue, e quindi sin log ax
è una funzione continua. Consideriamo la seconda funzione,
log a sin x. Appartengono al suo
dominio le sole x per
le quali sin x è positivo.
Ambedue le funzioni sin x
e log y sono continue;
e quindi la funzione composta è continua. Guardiamo ancora la seconda funzione della tabella,
log a sin x, ma questa volta
per x → 0. Il punto
y = 0 non appartiene
al dominio di log y
ed è
lim x→0 sin x = 0e lim y→0 log y = −∞.
Dunque, il Teorema 80 permette di affermare che
lim x→0 log a sin x = −∞.
In certi casi, il teorema 80 permette di calcolare i limiti per sostituzione ossia sostituendo
alla variabile y
una funzione invertibile ossia iniettiva e suriettiva
y = g(x)
che semplifichi la funzione da studiare, tale che la sua funzione inversa
g−1(y)
verifichi le ipotesi del teorema. Infatti, se
lim x→αg(x) = l, lim x→αf(g(x)) = m
allora
m = lim y→lf(g(g−1(y))) = lim
y→lf(y).
Vediamo un esempio:
Esempio 84 Si voglia calcolare
lim x→+∞1
x log xlog x.
La sostituzione
log x = t
mostra che questo limite è uguale a
lim t→+∞tt
et = lim t→+∞t
et = +∞. ■
2.3.3 Risultati “in negativo”
Il Teorema 80 si può applicare quando in particolare la funzione più interna ha
dominio ℕ,
ossia è una successione. In tal caso l’enunciato del teorema si riformula come
segue:
Teorema 85 Sia
lim n→+∞xn = α, lim x→αg(x) = β
(con i limiti α
e β
finiti o meno) e sia xn ∈ domg(x)
per ogni n.
Nel caso in cui α ∈ ℝ
assumiamo che g(x)
sia continua in α
oppure che α
non sia uno dei valori della successione. Allora,
lim n→+∞g(xn) = β.
Questo teorema si usa più spesso “in negativo”: se si trovano due successioni
{xn} e
{ξn} ambedue convergenti
ad α (che non
prendono valore α)
tali che
lim n→+∞g(xn)≠ lim n→+∞g(ξn),
allora non esiste lim x→αg(x)
(si confronti con quanto detto al paragrafo 2.1.5). Consideriamo ora la
funzione
sin log ax,a > 1.
Vogliamo provare che questa funzione non ammette limite per
x → 0. Per
questo consideriamo le due successioni cosìdefinite: |
log axn = −2nπ,ossia xn = a−2nπ,
log aξn = (−2nπ + π∕2),ossia ξn = a−2nπ+π∕2.
|
Si noti che, essendo a > 1,
si ha: lim xn = 0,
lim ξn = 0 e
inoltre
lim n→+∞ sin log axn = 0≠ lim n→+∞ sin log aξn = 1.
Dunque,
lim x→0 sin log axnon esiste.
In modo analogo si tratta il caso a ∈ (0, 1).
Queste osservazioni possono in particolare applicarsi per mostrare che non
esiste il limite di certe successioni. Per esempio, il limite della successione
{xn} = {sin nπ∕2} non
esiste. Infatti consideriamo le due sottosuccessioni
{x2n},{x2n+1}.
La prima converge a 0 mentre
la seconda converge ad 1
e quindi la successione {xn}
è priva di limite (si veda anche il Teorema 83).
Regole di calcolo e forme indeterminate di tipo esponenziale
Si voglia studiare il comportamento della funzione
f(x)g(x).
Il modo più semplice per farlo consiste nello scrivere la funzione come
f(x)g(x) = eg(x) log f(x);
studiare il comportamento dell’esponente ed usare il teorema della funzione
composta. Per esempio, se
f(x) → +∞,g(x) → +∞
allora
g(x) log f(x) → +∞e quindif(x)g(x) = eg(x) log f(x) = +∞.
Se però
f(x) → 1,g(x) → +∞,g(x) log f(x) è una forma indeterminata
e cosìnasce la forma indeterminata 1+∞.
Analoga origine hanno le altre “regole” o “forme indeterminate” di tipo
esponenziale.
2.4 Le funzioni iperboliche
Si chiamano funzioni iperboliche la funzioni
sinh x = ex − e−x
2 , cosh x = ex + e−x
2 .
I grafici di queste funzioni sono riportati in figura 2.6, a sinistra.
Si definiscono quindi le funzioni
tanh x = sinh x
cosh x = ex − e−x
ex + e−x, cotghx = cosh x
sinh x = ex + e−x
ex − e−x.
I grafici sono in figura 2.6, a destra. Spieghiamo la ragione del termine “funzioni
iperboliche”. Le “funzioni circolari” sono le usuali funzioni goniometriche
sin x e
cos x.
Si chiamano “funzioni circolari” perché la coppia
(x,y) = (cos 𝜃, sin 𝜃)
verifica l’equazione della circonferenza
x2 + y2 = 1;
e, viceversa, ogni punto della circonferenza trigonometrica si rappresenta
come (cos 𝜃, sin 𝜃).
Le funzioni iperboliche hanno questo nome perché la coppia
(x,y) = (cosh 𝜃, sinh 𝜃)
verifica l’equazione dell’iperbole equilatera
x2 − y2 = 1
e, viceversa, ogni punto di quest’iperbole ha coordinate
(cosh x, sinh x) per un’opportuna
scelta di x.
La verifica è immediata calcolando i quadrati di
cosh 𝜃 e
sinh 𝜃 e
sottraendo.
Questa formula va ricordata:
cosh 2x − sinh 2x = 1.
Dal punto di vista dei limiti, si ha:
|
|
|
| | | | | | | | | | |
| x → +∞ | x →−∞ | x → 0 | x → x0≠0 |
| | | | |
|
|
|
| | | | | |
| sinh x → +∞ | sinh x →−∞ | sinh x → 0 | sinh x → sinh x0 |
| | | | |
|
|
|
| | | | | |
| cosh x → +∞ | cosh x → +∞ | cosh x → 1 | cosh x → cosh x0 |
| | | | |
|
|
|
| | | | | |
| tanh x → 1 | tanh x →−1 | tanh x → 0 | tanh x → tanh x0 |
| | | | |
|
|
|
| | | | | |
| cotghx → 1 | cotgh x →−1 | | cotghx|→ +∞ | cotghx → cotanhx0 |
| | | | |
|
|
|
| | |
Dunque, le funzioni iperboliche sono continue. Le funzioni
sinh x e
tanh x sono
strettamente crescenti e quindi invertibili. Ammettono funzioni inverse che si
chiamano settore seno iperbolico e settore tangente iperbolica Le funzioni
cosh x e
cotanghx sono strettamente
crescenti su [0, +∞).
Le funzioni inverse delle loro restrizioni a tale intervallo si chiamano settore coseno iperbolico
e settore cotangente iperbolica Queste quattro funzioni si indicano con i simboli
settshx
settch x
sett thx e
settcthx. I
grafici delle quattro funzioni inverse sono in figura 2.7.
2.5 Confronto di funzioni
In presenza di forme indeterminate, in particolare quando si debba calcolare il
limite di un quoziente, si cerca di individuare, se esistono, i “termini dominanti”,
come nei due esempi seguenti:
Esempio 86 Si voglia calcolare
lim x→0x2 − 3x
x3 − x .
E’ chiaro che per x
“prossimo a 0”
sia x2
che x3
saranno via via meno importanti rispetto ad x.
Quindi scriveremo, per x≠0
x2 − 3x
x3 − x = − 3x
− x 1 − x∕3
1 − x2 = 31 − x∕3
1 − x2
e da qui si vede facilmente che
lim x→0x2 − 3x
x3 − x = 3.
D’altra parte, sia da calcolare
lim x→+∞x2 − 3x
x3 − x .
In questo caso dominano a numeratore l’addendo x2
ed a denominatore l’addendo x3.
Quindi scriveremo
x2 − 3x
x3 − x = x2
x3 1 − 3∕x
1 − 1∕x2 = 1
x 1 − 3∕x
1 − 1∕x2
e quindi
lim x→+∞x2 − 3x
x3 − x = 0. ■
Vogliamo introdurre delle definizioni che permettano di seguire quest’idea in casi più
generali di quelli dell’esempio precedente. Per questo si considerano due funzioni
f(x) e
g(x) (con lo stesso dominio).
Supponiamo inoltre g(x)
non zero. Si dice che f
è o piccolo di g
(per x
tendente a α)
se accade che
lim x→αf(x)
g(x) = 0.
Come notazione, si scrive
f = o(g)
Si noti che la notazione “o”
non fa comparire α.
La definizione riguarda il limite per
x → α,
ma chi sia α
va dedotto dal contesto. Ovviamente, in
un breve esercizio ciò sarà impossibile e
α
andrà esplicitamente specificato.
In questa definizione, non si richede che
f oppure
g siano infiniti o infinitesimi.
Per esempio, se g(x) ≡ 1,
la notazione
f = o(1) significa lim x→αf(x) = 0.
Ossia, si scriverà
f = o(1)
per scrivere che f(x) è
un infinitesimo per x → α.
Però, a parte questo singolo caso, di regola l’uso del simbolo di Landau
“o”
si incontra quando le due funzioni sono infiniti o infinitesimi per
x → α, ossia
come si dice, sono infiniti o infinitesimi contemporanei. L’interpretazione del
significato del simbolo di Landau varia a seconda che si lavori con infiniti oppure
con infinitesimi. Infatti:
Siano f(x)
e g(x)
due infiniti per x → α.
Allora, la condizione
lim x→αf(x)
g(x) = 0
intuitivamente significa che f(x)
diverge più lentamente di g(x).
Per questo, quando f = o(g)
ed f(x)
e g(x)
sono infiniti si dice che f(x)
è infinito di ordine inferiore a g(x)
o che g(x)
è infinito di ordine superiore ad f(x)
(sottinteso: per x → α).
Invece:
Siano f(x)
e g(x)
due infinitesimi per x → α.
Allora, la condizione
lim x→αf(x)
g(x) = 0
intuitivamente significa che f(x)
tende a zero più velocemente di
g(x).
Per questo, quando f = o(g)
ed f(x)
e g(x)
sono infinitesimi si dice che f(x)
è infinitesimo di ordine superiore a g(x)
o che g(x)
è infinitesimo di ordine inferiore ad f(x)
(sottinteso: per x → α).
Per esercizio, passando ai reciproci, si riformulino le due proprietà appena esaminate
supponendo che |f(x)∕g(x)|→ +∞.
Se accade che |
lim x→αf(x)
g(x) = l ∈ ℝ,l≠0
| (2.16) |
si dice che i due infiniti (o infinitesimi)
f(x) e
g(x) hanno lo
stesso ordine di grandezza (brevemente, diremo che “hanno lo stesso ordine”) per
x → α e
scriveremo
f ≍ gsottinteso, per x → α.
Se il limite in (2.16) non esiste, si dice che i due infiniti o infinitesimi
f(x) e
g(x) non sono confrontabili
per x → α. Se
invece il limite esiste, finito o meno, si dice che essi sono confrontabili Siano ancora
f(x) e
g(x) due infiniti oppure
due infinitesimi (per x → α).
Si dice che essi sono equivalenti se
f(x) = g(x) + o(g).
In tal caso si scrive
f ∼ g,
al solito sottintendendo “per x → α”.
Dividendo i due membri per g(x)
e passando al limite, si vede che
Teorema 87 I due infiniti o infinitesimi contemporanei f(x)
e g(x)
sono equivalenti (per x → α)
se e solo se
lim x→αf(x)
g(x) = 1.
D’altra parte,
lim x→αf(x)
g(x) = 1⇒ lim x→α g(x)
f(x) = 1.
Dunque,
Corollario 88 Vale
f ∼ g
se e solo se
g ∼ f
e ciò accade se e solo se
g(x) = f(x) + o(f).
Infine, può accadere che esistano numeri reali
c e
γ con
c≠0 e tali
che
f(x) ∼ c[g(x)]γ.
In questo caso si dice che:
- f(x)
è un infinito oppure un infinitesimo di ordine γ
rispetto a g(x);
- la funzione c[g(x)]γ
si chiama la parte principale di f(x)
rispetto a g(x).
Osservazione 89 Va notato che due infinitesimi o infiniti possono essere
confrontabili, senza che esista l’ordine dell’uno rispetto all’altro, ossia senza
che esista la parte principale dell’uno rispetto all’altro. Per fare un esempio,
consideriamo le due funzioni
f(x) = log x,g(x) = x.
Si tratta di due infiniti per
x → +∞
e usando i risultati nella tabella 2.4 si vede che
lim x→+∞f(x)
g(x) = 0.
Dunque i due infiniti sono confrontabili, e g(x)
è di ordine superiore rispetto ad f(x).
Però, ancora dalla tabella 2.4, si vede che
lim x→+∞ f(x)
gα(x) = lim x→+∞ log x
xα = 0 seα ≥ 0 + ∞ se α < 0.
Quindi, non esiste l’ordine di log x
rispett a g(x) = x
e dunque nemmeno la parte principale. ■
Simboli di Landau
I simboli ∼,
≍ ed
o
si chiamano simboli di Landau dal nome del matematico tedesco che li
ha introdotti. Esistoni altri simboli di Landau. In particolare si dice che
f è
O grande di g
(per x → α) se
esiste M ed
un intorno I
di α
tale che
x ∈ I⇒|f(x)| < M|g(x)|.
Se ciò accade si scrive
f = O(g).
Si noti un caso particolare: se esiste finito
lim x→αf(x)
g(x) = l
allora f = O(g) (in un
opportuno intorno di α).
Infine, un’osservazione sul significato del simbolo
≍. Di questo
abbiamo dato una definizione assai particolare. Specialmente in testi di fisica, si scrive
f ≍ g quando
esistono m > 0
ed M
tali che
m|g(x)|≤|f(x)|≤ M|g(x)|
almeno in un intorno di un sottinteso
α,
senza richiedere l’esistenza del limite in (2.16).
2.5.1 Infiniti e infinitesimi di confronto fondamentali e formule da
ricordare
Se non c’è ragione di fare diversamente, usa confrontare un infinito o un infinitesimo
f(x) con
funzioni gx)
particolari, dette gli infiniti o gli infinitesimi di confronto fondamentali. Questi sono
riportati nella tabella 2.6.
Table 2.6: Infiniti e infinitesimi di confronto fondamentali
x tende a
infinito fondamentale
infinitesimo fondamentale
0
1
|x|
|x|
x0
1
|x − x0|
|x − x0|
+∞
x
| 1
x |
−∞ |
|x|
1
|x|
Alcuni dei limiti elencati al paragrafo 2.1.10 si possono riformulare
come segue: Ciascuno degli infiniti seguenti è di ordine minore
del successivo:
{log n},{nb},{an},({n!},{nn}
perché
lim log n
na = 0se a > 0;
lim nb
an = 0 se a > 1, b > 0; lim an
n! = 0se a > 1;
lim n!
nn = 0.
Formule di MacLaurin Vanno ricordate subito le formule della tabella 2.7,
che sono casi particolari della formula di MacLaurin che si studierà più avanti. Le
ultime due righe della tabella si riferiscono a funzioni probabilmente note ad alcuni
studenti, ma non a tutti. Esse verranno introdotte al paragrafo 2.4. Per
interpretare le formule di MacLaurin, vanno conosciuti i simboli seguenti:
- il simbolo n!
che si legge n fattoriale
il numero n
deve essere intero non negativo.
Per definizione, 0! = 1
ed 1! = 1. Il
simbolo n!
per n > 1 si
definisce per ricorrenza:
n! = n(n − 1)!;
e quindi,
2! = 2 ⋅ 1! = 2 ⋅ 1 = 2,3! = 3 ⋅ 2 ⋅ 1 = 6,4! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24,…
- il simbolo γ
k ,
che si chiama coeffciente binomiale il numero k
deve essere intero non negativo mentre il numero γ
può essere reale qualsiasi.
Per definizione, |
γ
0 = 1, γ
1 = (γ − 0)
1! = γ
1
|
Quindi si definisce
γ k = γ(γ − 1)(γ − 2)⋯ γ − (k − 1)
k! .
Per esempio, |
1∕2 2 = (1∕2) (1∕2) − 1
2! = −1
4 1
2 = −1
8
1∕2 3 = (1∕2) (1∕2) − 1 (1∕2) − 2
3! = 3
8 1
6 = 1
16.
|
Si noti che se γ = n,
intero positivo, allora
n n = 1, n n + 1 = 0
e quindi
n k = 0,∀k > n.
Ciò detto, le formule da ricordare sono nella tavola 2.7.
Table 2.7: Formule di MacLaurin da usare quando
(x → 0
a)
sin x = x −x3
3! + x5
5! + ⋯ + (−1)k x2k+1
(2k+1)! + o(x2k+2)
b)
cos x = 1 −x2
2! + x4
4! + ⋯ + (−1)k x2k
(2k)! + o(x2k+1)
c)
tan x = 1 −x2
2! + x4
4! + ⋯ + (−1)k x2k
(2k)! + o(x2k+1)
d)
tan x = x −x3
3 + x5
5 + ⋯ + (−1)nx2n+1
2n+1 + o(x2n+2)
e)
(1 + x)γ = ∑
k=0nγ
kxk + o(xn)
f)
log e(1 + x) = x −x2
2 + x3
3 + ⋯ + (−1)(n−1)xn
n + o(xn)
g)
ex = 1 + x
1! + x2
2! + ⋯ + xn
n! + o(xn)
h)
sinh x = x + x3
3! + x5
5! + ⋯ + x2k+1
(2k+1)! + o(x2k+2)
i)
cosh x = 1 + x2
2! + x4
4! + ⋯ + x2k
(2k)! + o(x2k+1)
La formula e) si chiama formula del binomio o formula di Newton Nel caso particolare
in cui γ sia
intero, γ = n,
allora
(1 + x)n = ∑
k=0nn
kxk + o(xn) = ∑
k=0n+1n
kxk + o(xn+1)
perché si è visto che n
n+1 = 0.
In questo caso vale di più: si ha |
(1 + x)n = ∑
k=0nn
kxk;
| (2.17) |
ossia, in questo caso l’errore o(xn)
è in realtà identicamente zero.
Anche la formula (2.17) si chiama formula di Newton
2.6 Appendice: ancora sulla formula del binomio di Newton
Consideriamo due casi particolari della formula binomiale:
- Si sostituisca x
con −x e si
prenda a = −1.
In questo modo
|
(1 − x)−1 = ∑
k=0n−1
k (−x)k + o(xn)
= 1 + x + x2 + ⋯ + xn + o(xn).
|
In questo caso si può trovare un’espressione esplicita per
o(x). Per questo si consideri
il prodotto notevole
|
(1 − x)(1 + x + x2 + ⋯ + xn) = 1 − xn+1
ossia 1 + x + x2 + ⋯ + xn = 1 − xn+1
1 − x = (1 − x)−1 − xn+1
1 − x.
|
Si ha dunque:
(1 − x)−1 = 1 + x + x2 + ⋯ + xn + xn+1
1 − x
e quindi
o(xn) = xn+1
1 − x.
- Si noti che se n ∈ ℕ,
n
k = 0 sek > n.
Dunque, se r > n,
si ha |
(1 + x)n = ∑
k=0rn
kxk + o(xr) = ∑
k=0nn
kxk + o(xr).
| (2.18) |
Vogliamo provare che in realtà o(xr) = 0,
ossia che vale la formula del binomio di Newton. Notiamo
che il membro sinistro di (2.18) è un polinomio di grado
n:
(1 + x)n = a
0 + a1x + a2x2 + ⋅ + a
nxn.
Notiamo che il coeffciente di x0
è 1 in ambedue i
membri, ossia che a0 = 1.
Sottraendolo si ha
(1 + x)n − 1 = ∑
k=1nn
kxk + o(xr).
La funzione o(xr)
non è cambiata. Dividendo i due membri per
x e calcolando il
limite per x → 0 si vede
che x ha lo stesso
coeffciente a1 nei
due membri.
Sottraendo a1x
dai due membri si trova
(1 + x)n − 1 − a
1x = ∑
k=2nn
kxk + o(xr).
La funzione o(xr)
non è cambiata. Ora il procedimento si può ripetere, notando che
x2 ha lo stesso
coeffciente a2
nei due membri cosìche
(1 + x)n − 1 − a
1x − a2x2 = ∑
k=3nn
kxk + o(xr)
e ciò non cambia la funzione o(xr).
Ripetiamo il procedimento. Dopo aver sottratto anche
anxn
ai due membri si trova
o(xr) = 0
Dunque, la (2.18) in realtà vale con
o(xr) = 0,
ossia si ha
(1 + x)n = ∑
k=0nn
kxk.
Ciò giustifica la formula di Newton (2.17). Sostituendo
x con
b∕a e moltiplicando i
due membri per an
si trova
(a + b)n = ∑
k=0nn
kan−kbk.
Anche questa formula si chiama formula di Newton
2.7 Alcuni esercizi
- Spiegare perché l’affermazione seguente è falsa: se x0
non è punto di accumulazione di A,
allora è punto isolato di A.
- Usando opportuni esempi, provare che ambedue le affermazioni seguenti
sono sbagliate: 1) la funzione f(x)
è continua in x0
se lim x→x0−f(x) = lim x→x0+f(x);
2) la funzione f(x),
definita in x0,
è continua in x0
se lim x→x0−f(x) = lim x→x0+f(x).
- In ciascuna delle coppie di uguaglianze seguenti, una è corretta e l’altra
sbagliata. Si spieghi il motivo.
lim x→−∞ log x2 = lim
x→−∞2 log x
lim x→−∞ log x2 = lim
x→−∞2 log |x| lim x→−∞x2 = lim x→−∞2x
lim x→−∞x2 = lim x→−∞2|x|.
Se invece il limite è per x → +∞?
- Sia
pn = 1 ⋅1
2 ⋅1
3⋯1
n.
Mostrare che
lim n→+∞pn = 0.
- Sia
sn = 1 + q + q2 + ⋯ + qn.
Si studi lim n→+∞sn,
per ogni valore del parametro reale q
(si ricordi la (1.6)).
- Dire se esiste f(x),
definita su ℝ,
positiva e con lim x→+∞f(x) < 0.
Giustificare la risposta.
- Si consideri l’insieme A = ∪n=2+∞(1∕n, 1∕(n − 1)).
Calcolare sup A
ed inf A
e trovare due successioni, {an}
e {bn},
a valori in A
e tali che
lim n→+∞an = inf A, lim n→+∞bn = sup A.
- L’insieme A
è ancora quello dell’esercizio 7. Si dica se si possono trovare successioni
{an}
e {bn}
per cui vale
lim n→+∞an = inf A, lim n→+∞bn = sup A
ma che non prendono valori in A.
- Sia A
l’insieme dell’esercizio 7 e sia B = {−1}∪ A.
Dire se esistono successioni {an}
e {bn}
a valori in A
e tali che
lim n→+∞an = inf B, lim n→+∞bn = sup B.
Spiegare come cambia la risposta se invece si chiede che le successioni
abbiano valori in B.
- (⋆)
Dire se esiste una funzione positiva, priva di limite per x → 0
e illimitata in ogni intorno di 0.
- Tracciare qualitativamente il grafico della funzione
f(x) = 1
[sin 2x]
([⋅]
indica la parte intera) e, se esiste, calcolarne il limite per x → +∞.
- (⋆)
Trovare una funzione pari ed una funzione dispari, limitate e prive di
limite per x → 0.
- Mostrare che se f(x)
è pari e se lim x→0+f(x) = l
allora si ha anche lim x→0f(x) = l.
Cosa accade se la funzione è dispari?
- Dire se esiste una funzione periodica dotata di limite per x → +∞.
- Sia f(x)
una funzione periodica tale che lim x→+∞|f(x)| = 1.
Dire se f(x)
è costante.
- Sia f(x)
una funzione dispari che ha un salto per x = 0.
Provare che x = 0
è discontinuità eliminabile di |f(x)|.
- Si trovi una funzione f(x)
definita su [−1, 1]
e non costante, tale che
lim x→x0f(x) = 1per ogni x0 ∈ [−1, 1].
- (⋆)
Si trovi una funzione definita su (0, 1],
che ha infiniti punti di discontinuità e tale che lim x→x0f(x) = 0
per ogni x0 ∈ (0, 1].
- (⋆)
Dire se esiste una funzione illimitata su (0, 1]
e tale che lim x→x0f(x) = 0
per ogni x0 ∈ (0, 1].
- (⋆)
Dire se esiste una funzione definita su ℝ,
illimitata e tale che per ogni x0 ∈ ℝ
si abbia:
lim x→x0f(x) = 1.
- (⋆)
Siano f(x)
e g(x)
definite su [0, +∞)
e sia f(x) > g(x) > 0.
Si tracci il grafico della funzione ϕ(x)
tale che
ϕ(2n) = g(2n),ϕ(2n + 1) = f(2n + 1)
e il cui grafico negli altri punti è ottenuto congiungendo successivamente
(2n,ϕ(2n)) e
(2n + 1,ϕ(2n + 1))
mediante segmenti di retta. Quindi:
- supponiamo che f
sia un infinito di ordine superiore a g.
Mostrare che non è vero che ϕ
è un infinito di ordine superiore a g.
- (⋆)
Si faccia un esempio per provare che le disuguaglianze
seguenti possono non valere nemmeno se le due funzioni
f(x) e
g(x)
sono strettamente crescenti:
|
g(x) ≤ ϕ(x) ≤ f(x);
| (2.19) |
- (⋆)
si mostri che le disuguaglianze (2.19) valgono se le due funzioni
f(x) e
g(x)
sono convesse;
- si provi che se lim x→+∞f(x) = lim x→+∞g(x) = α (finito
o meno) si ha anche lim x→+∞ϕ(x) = α
(l’asserto vale sempre, ma si prova più facilmente se le funzioni sono
strettamente convesse);
- si provi che se f ∼ g
allora si ha anche ϕ ∼ f
e quindi ϕ ∼ g
(l’asserto vale sempre, ma si prova più facilmente se le funzioni sono
strettamente convesse).
- (⋆)
Sia f(x) > g(x) > 0
per x > 0.
Le due funzioni siano strettamente crescenti ed illimitate e valga, per
x → +∞,
f = o(g).
Sia ϕ(x) = f(x)g(x). Dire se è
vero o meno che ϕ = o(f),
ϕ = o(g),
f = o(ϕ),
g = o(ϕ) (sempre
per x → +∞).
- Sia f(x) ∼ xn (per
x → +∞). Si chiede se
esiste un numero c
tale che, per x → +∞,
sia log f(x) − c log x = o(1).
- Trovare un esempio di funzione f(x)
tale che f(x) = o(x) (per
x → 0) ma per cui
NON vale né log f(x) = o log x
né 1
log f(x) = o 1
log x
(suggerimento: si provi con le potenze).
- Sia f(x)
definita su ℝ
e sia
g(x) = max{f(s)|s ≤ x}.
Si scelga come f(x)
una delle funzioni −x2,
x2,
sin x
e si tracci il grafico della corrispondente funzione
g(x).
- Sia f(x)
continua su ℝ
e sia
g(x) = max{f(s)|s ≤ x}.
Si mostri che g(x) è
continua. Può essere che g(x)
sia continua anche se f(x)
non è continua? Si considerino i due casi
f(x) = sgn(x) ed
f(x) = − sgn(x).
- (⋆) Per
ogni n > 1
si considerino le funzioni definite sull’intervallo
[0, 1]
come segue:
fn(x) = 0 se0 ≤ x ≤ 1∕n
n se1∕n < x < 2∕n
0 se2∕n ≤ x ≤ 1.
fissato x ∈ [0, 1],
si consideri la successione di numeri
{fn(x)}. Si provi che
questa converge a 0
per ogni x ∈ [0, 1].
- (⋆) Si trovi una funzione
definita su x > 0, iniettiva
e tale che lim x→+∞f(x) = +∞ e tale che
inoltre non esista lim x→+∞f−1(x).
Table 2.8: Regole di calcolo e forme indeterminate
|
|
| | | | | | Regole | +∞ + ∞ = +∞ | −∞ − ∞ = −∞ |
| | | | |
|
| | | | |
| | (+∞)(+∞) = +∞(−∞)(−∞) = +∞
| (−∞)(+∞) = −∞ = (+∞)(−∞) |
| | | | |
|
| | | | |
| | ±∞
0 = +∞ | 0
±∞ = 0 |
| | | | |
|
| | | | |
| | l + (+∞) = l + ∞ = +∞l + (−∞) = l − ∞ = −∞
| l(+∞) = + ∞se l >0 − ∞se l <0 |
| | | |
|
|
| | | | |
| | 0+∞ = 0
0−∞ = +∞ | (+∞)+∞ = +∞
(+∞)−∞ = 0 |
| | | |
|
|
| | | | |
| Forme indeterminate | +∞−∞ | 0 ⋅ (±∞) |
| | | |
|
|
| | | | |
| | ±∞
±∞ | 0
0 |
| | | |
|
|
| | | | |
| | 00 (+∞)0 | 1±∞ |
| | | |
|
|
| | |
Capitolo 3
Velocità, tangenti e derivate
Tutte le leggi sono dettate dall’esperienza, ma
per enunciarle ci vuole un linguaggio speciale;
il linguaggio ordinario è troppo povero e vago
per esprimere dei rapporti cosìdelicati, ricchi
e precisi. Ecco quindi una ragione perchè il
fisico non possa ignorare la matematica. Henri
Poincaré Il valore della scienza
In questo capitolo proseguiamo nello studio delle proprietà locali delle funzioni,
studiandone la proprietà di derivabilità, suggerita dalla meccanica per il calcolo
della velocità istantanea e dell’accelerazione istantanea, e dalla geometria per la
definizione della retta tangente al grafico di una funzione.
3.1 La derivata
Supponiamo che un punto si muova lungo l’asse delle ascisse, e che all’istante
t la sua posizione
sia x(t). Abbiamo
cioè una funzione t↦x(t)
che rappresenta il moto del punto. fissiamo un intervallo di tempo di estremi
t0 e
t0 + h (a destra o a
sinistra di t0).
Si chiama velocità media del punto su quest’intervallo il numero
x(t0 + h) − x(t0)
h .
Può accadere che esista finito
lim h→0x(t0 + h) − x(t0)
h .
In fisica, questo numero si chiama “velocità istantanea” del punto all’istante
t0 e si indica col
simbolo v(t0) oppure con
uno dei simboli
x′(t
0) oppure
ẋ(t0).
Va detto subito che la velocità media esiste sempre, mentre la velocità
istantanea può esistere o meno. Per esempio non esiste negli istanti nei quali si
verificano degli urti. Se la velocità istantanea esiste per ogni valore di
t,
allora si può definire l’“accelerazione media” sull’intervallo di estremi
t0 e
t0 + h
come
v(t0 + h) − v(t0)
h .
Se il limite seguente esiste, questo si chiama l’“accelerazione istantanea” all’istante
t0:
lim h→0v(t0 + h) − v(t0)
h .
In ambedue i casi, si incontra quindi un rapporto con al numeratore
l’incremento del valore di una funzione al passare del suo argomento da
t0, fissato, a
t0 + h e al denominatore
l’incremento h della variabile
indipendente. L’incremento h
può essere positivo oppure negativo. Questo rapporto si chiama rapporto incrementale
della funzione che si sta considerando; e del rapporto incrementale si deve fare il limite per
h → 0. Un problema
analogo si incontra in geometria, quando si cerca di definire la tangente al grafico di una funzione
f(x) definita su
un intervallo [a,b].
Sia x0 ∈ (a,b).
Si vuol definire la tangente al grafico della funzione nel punto
(x0,f(x0)).
Per questo consideriamo la secante che congiunge i due punti
(x0,f(x0)), considerato
fisso, e il punto (x0 + h,f(x0 + h)),
variabile sul grafico. Il coeffciente angolare della secante è
f(x0 + h) − f(x0)
h
e quindi la secante è la retta
y = f(x0) + f(x0 + h) − f(x0)
h (x − x0).
Se esiste il limite per h → 0
di questi coefficienti angolari,
m0 = lim h→0f(x0 + h) − f(x0)
h ,
la retta
y = f(x0) + m0(x − x0)
si chiama retta tangente al grafico di f(x)
nel punto (x0,f(x0)).
Si veda la figura 3.1.
Si vede da qui che il limite del rapporto incrementale compare in applicazioni
diverse, e ce ne sono ancora molte altre. Quindi, questo limite va studiato in
generale.
Definizione 90 Sia f(x)
definita su un intervallo (a,b)
e sia x0 ∈ (a,b).
Se esiste finito il numero
lim h→0f(x0 + h) − f(x0)
h ,
questo si chiama la derivata della funzione
f(x)
in
x0
e si indica con uno dei simboli
f′(x
0),ḟ(x0),Dx0f,Df(x0), d
dxf(x0).
Un’altra notazione si vedrà più avanti. Il simbolo
dd
xf(x0) è
dovuto a Leibniz e ricorda che la derivata è il limite di un quoziente. NON è
un quoziente e quindi il simbolo non indica una frazione. La notazione
dd
x,
di proposito evidenziata in colore, va letta come simbolo unico. Si
osservi che la derivata deve essere un numero. Non può essere
+∞ oppure
−∞.
Infatti, molte delle proprietà delle funzioni derivabili che vedremo NON valgono
quando il limite del rapporto incrementale esiste, ma non è finito. Per esempio:
Teorema 91 Se la funzione f(x)
è derivabile in x0
essa è continua in x0.
Dim. Infatti,
f(x0 + h) − f(x0) = hf(x0 + h) − f(x0)
h .
Per ipotesi, il limite del rapporto incrementale esiste finito e quindi
0 = lim h→0h f(x0 + h) − f(x0)
h = lim h→0 f(x0 + h) − f(x0) ;
ossia, posto x = x0 + h
ed usando il teorema dei limiti delle funzioni composte,
lim x→x0f(x) = f(x0). ■
Esempio 92 Il risultato precedente non vale
se il limite del rapporto incrementale è
+∞.
Per vederlo, si consideri la funzione sgnx
in x0 = 0.
Essa è discontinua. Il limite del rapporto incrementale esiste, ma non è un
numero:
lim h→0 sgnh
h = +∞. ■
Un’altro punto a cui fare attenzione è questo: la derivata
si definisce solo nei punti interni al dominio della funzione. Se
x0 = a oppure
x0 = b si
possono studiare i due limiti
lim h→0+f(a + h) − f(a)
h , oppure lim h→0−f(b + h) − f(b)
h .
Se uno dei limiti esiste,
finito o meno, esso si chiama la derivata direzionale in
a oppure
in b.
La derivata direzionale si può talvolta definire anche in punti
x0 di
non derivabilità. Se esiste, finito o meno, uno dei due limiti
lim h→0+f(x0 + h) − f(x0)
h , oppure lim h→0−f(x0 + h) − f(x0)
h
questo si chiama la derivata direzionale,rispettivamente destra oppure sinistra, di
f(x) in
x0. La
derivata direzionale destra o sinistra si indica con uno dei simboli
D+f(x0),f+′(x
0),D−f(x0),f−′(x
0).
Sottolineiamo che, a differenza della derivata, la derivata direzionale
non è necessariamente finita.
Una dimostrazione del tutto analoga a quella del Teorema 91 mostra che:
Teorema 93 Se in x0 ∈ [a,b]
esiste finita la derivata destra (o sinistra) di
f(x),
allora la funzione f(x)
è continua da destra (rispettivamente, da sinistra) in
x0.
Concludiamo con una definizione il cui interesse apparirà
principalmente nei corsi successivi. Si chiama differenziale della funzione
f(x) in
x0 la
funzione
h↦f′(x
0)h.
Questa trasformazione si indica spesso col simbolo
df.
Il significato geometrico del differenziale è illustrato al paragrafo 3.2.
Esempio 94 Calcoliamo la derivata di alcune potenze. Se
f(x) ≡ c,
costante, allora f(x0 + h) − f(x0) = 0
per ogni h.
Il rapporto incrementale è nullo e tale è il suo
limite: la derivata di una funzione costante è nulla. Sia
f(x) = x.
Allora,
lim x→x0f(x) − f(x0)
x − x0 = lim x→x0x − x0
x − x0 = lim h→01 = 1.
Sia f(x) = x2.
Allora, f(x) − f(x0) = x − x02 = (x − x
0)(x + x0).
Dunque,
lim x→x0f(x) − f(x0)
x − x0 = lim x→x0 x + x0 = 2x0.
In generale, si ricordi la formula per la somma dei primi
n
termini di una progressione geometrica:
1 + x + x2 + ⋯ + xn−1 = 1 − xn
1 − x = xn − 1
x − 1 .
Si ha quindi |
xn − x
0n
x − x0 = x0n
x0 1 − (x∕x0)n
1 − (x∕x0)
= x0n−1 1 + (x∕x
0) + (x∕x0)2 + ⋯ + (x∕x
0)n−1 .
|
Gli addendi in parentesi sono in numero di
n e ciascuno di
essi tende ad 1
per x → x0.
Dunque,
Dx0xn = lim
x→x0xn − x
0n
x − x0 = nx0n−1.
Sia ora
f(x) = 1
x.
Il rapporto incrementale in x0
è
(1∕x) − (1∕x0)
x − x0 = 1
xx0 x0 − x
x − x0 = − 1
xx0
e quindi
Dx0 1
x = lim x→x0(1∕x) − (1∕x0)
x − x0 = − 1
x02. ■
3.1.1 La funzione derivata e le derivate successive
Ricordiamo che la derivata è un numero che si associa ad un punto
x0:
f′(x
0).
Può essere però che tale numero esista per ogni
x ∈ (a,b) o per
ogni x ∈ (a,c) ⊆ (a,b).
In tal caso si costruisce una funzione
x↦f′(x)
che si chiama la funzione derivata di f(x).
Può accadere che la funzione derivata sia ulteriormente derivabile (come
deve essere per definire l’accelerazione). In questo caso, si può calcolare il
numero
lim h→0f′(x
0 + h) − f′(x
0)
h
che si chiama la derivata seconda di f(x)
in x0. In
questo contesto, la “derivata” si chiama anche derivata prima La derivata seconda
si indica con uno dei simboli
f″(x0),Dx02f,D2f(x
0), d2
dx2f(x0).
In meccanica, si usa anche il simbolo di Newton
f..(x0).
Ovviamente:
Teorema 95 Se la funzione f(x)
ammette derivata seconda in ogni punto di
(a,b)
allora sia f(x)
che f′(x)
sono continue su (a,b).
Quanto detto si può ora ripetere: se la derivata seconda esiste in ogni punto si
può cercare di derivarla, definendo, se esiste, la derivata terza, quarta,
n-ma
ecc. Le derivate successive si indicano con i simboli
Dx0nf,Dnf(x
0), dn
dxnf(x0).
Ovviamente, le notazioni con gli apostrofi o i punti non sono pratiche
oltre al terzo ordine. In certe formule, conviene indicare la derivata
n-ma in
x0 col
simbolo
f(n)(x
0)
e in questo contesto si definisce
f(0)(x
0) = f(x0).
Sottolineiamo che se esiste la derivata
n-ma in ogni
punto di (a,b),
esistono le derivate precedenti, e sono continue in ogni
punto di
(a,b). Invece l’esistenza
di f(n)(x) nel solo punto
x0 implica l’ esistenza
della derivata f(n−1)(x)
in un intorno di I
di x0
e quindi le derivate precedenti a quella di ordine
n − 1 sono continue
su I mentre la
f(n−1)(x) è continua in
x0 ma potrebbe
essere discontinua in ogni altro punto. Una funzione che ammette le derivate fino all’ordine
n incluso su
(a,b), continue si
dice di classe Cn
e si scrive
f ∈ Cn(a,b).
Scrivendo
f ∈ C0(a,b)o anche f ∈ C(a,b)
si intende dire che f(x)
è continua su [a,b].
Scrivendo f(x) ∈ C∞(a,b)
(leggi f(x) di
classe C∞
su (a,b)) si
intende che la funzione ammette derivate di ogni ordine in ciascun punto di
(a,b).
3.2 La prima formula degli incrementi finiti
La sostituzione h = x − x0
mostra che
f′(x
0) = lim x→x0f(x) − f(x0)
x − x0
ossia, essendo f′(x
0)
un numero,
lim x→x0 f(x) − f(x0)
x − x0 − f′(x
0) = 0.
Dunque, usando il simbolo di Landau,
f(x) = f(x0) + f′(x
0)(x − x0) + (x − x0) o(1).
Ma,
(x − x0) o(1) = o(x − x0).
Dunque,
la derivata f′(x
0),
se esiste, è quel numero m
tale che
f(x) = f(x0) + m(x − x0) + o(x − x0).
Dunque,
f′(x
0)
verifica
f(x) = f(x0) + f′(x
0)(x − x0) + o(x − x0).
Questa formula si chiama prima formula degli incrementi finiti Viceversa,
se esiste m ∈ ℝ
tale che |
f(x) = f(x0) + m(x − x0) + o(x − x0)
| (3.1) |
allora
m = lim x→x0 f(x) − f(x0)
x − x0 + o(x − x0)
x − x0 = lim x→x0f(x) − f(x0)
x − x0 = f′(x
0).
Quindi, la prima formula degli incrementi finiti è anche una
equivalente definizione di derivata: la derivata è quel numero
m per il
quale è verificata l’uguaglianza (3.1). Ciò ha una conseguenza utile per il calcolo
di certe derivate:
Teorema 96 Sia f(x)
definita in un intorno di x0.
Se per x → x0
vale |
f(x) − f(x0) = o(x − x0)
| (3.2) |
allora f′(x
0)
esiste e
f′(x
0) = 0.
Dim. Infatti, la (3.2) coincide con la prima formula degli incrementi finiti (3.1) scritta con
m = 0. ■
Nella prima formula degli incrementi finiti compare la funzione
(x − x0) → f′(x
0)(x − x0)
che abbiamo chiamato il differenziale della funzione
f(x) in
x0. La prima
formula degli incrementi finiti combinata con l’equazione della retta tangente al grafico
di f(x) in
(x0,f(x0)),
ossia
y = f(x0) + f′(x
0)(x − x0),
mostra il significato geometrico del differenziale:
f(x) − f(x0) è
l’incremento della quota del punto del grafico della funzione, quando si passa
da x0 ad
x.
Invece,
f′(x
0)(x − x0) = f(x0) + f′(x
0)(x − x0) − f(x0).
Dunque, il differenziale indica l’incremento dell’ordinata del punto della tangente quando
ci si sposta da x0
ad x e
questo incremento differisce dal corrispondente incremento di ordinata sul
grafico della funzione per infinitesimi di ordine superiore al primo rispetto ad
h = (x − x0), ossia rispetto
all’incremento h
dato all’ascissa. Ciò è illustrato in figura 3.2.
3.3 Regole di calcolo per le derivate prime
Ci sono quattro regole per il calcolo delle derivate: la derivata della somma, del
prodotto, della funzione composta e della funzione inversa. Inoltre, esiste una
formula per la derivata di un quoziente, che si ottiene dalle precedenti.
Derivata di una somma Il limite di una somma è uguale alla
somma dei limiti (quando ambedue esistono finiti). Dunque, se
f e
g sono
derivabili in x0
vale
Dx0 f(x) + g(x) = f′(x
0) + g′(x
0).
Derivata del prodotto La formula per la derivata del prodotto si chiama
formula di Leibniz e si vede meglio partendo dalla prima formula degli incrementi
finiti. Se f(x)
e g(x) sono
derivabili in x0
vale
|
f(x) = f(x0) + f′(x
0)(x − x0) + o1(x − x0),
g(x) = g(x0) + g′(x
0)(x − x0) + o2(x − x0).
|
Moltiplicando membro a membro si ha |
f(x)g(x) = f(x0)g(x0) + f′(x
0)g(x0) + f(x0)g′(x
0) (x − x0)
+ f(x0) + f′(x
0)(x − x0) o2(x − x0)
+ g(x0) + g′(x
0)(x − x0) o1(x − x0)
+f′(x
0)g′(x
0)(x − x0)2 + o
1(x − x0) o2(x − x0) .
|
La parentesi graffa è o(x − x0)
e quindi
lim x→x0f(x)g(x) − f(x0)g(x0)
(x − x0) = f′(x
0)g(x0) + f(x0)g′(x
0).
Vale quindi la formula di Leibniz
Dx0 f(x)g(x) = f′(x
0)g(x0) + f(x0)g′(x
0).
Supponiamo che g(x) ≡ c
sia costante. Allora,
g′(x
0) = lim h→0g(x0 + h) − g(x0)
h = lim h→0c − c
h = 0.
Dunque,
d
dx cf(x0) = cf′(x
0).
Combinando quest’osservazione con la regola di derivazione della somma, si
trova:
quando
a
e
b
sono numeri
Dx0 af(x) + bg(x) = af′(x
0) + bg′(x
0).
Questa regola si chiama linearità della derivata.
Derivata della funzione composta Siano ora
f(x) e
g(x)
due funzioni e supponiamo che la funzione composta
f(g(x)) sia definita su un
intervallo (a,b). Sia
x0 ∈ (a,b) e supponiamo
che g(x) sia
derivabile in x0
mentre f(x) sia
derivabile in y0 = g(x0).
Allora vale
Dx0f(g(x)) = f′(g(x
0))g′(x
0).
I colori sono stati usati per evidenziare il fatto che la derivata della funzione
composta si calcola iniziando col derivare la funzione più esterna. La
dimostrazione è semplice: per ipotesi valgono le due formule degli incrementi finiti
|
g(x) = g(x0) + g′(x
0)(x −x0) + o(x −x0)
f(y) = f(y0) + f′(y
0)(y −y0) + o(y −y0)
|
e inoltre
y0 = g(x0)
Si tenga conto di ciò e si sostituisca y
con g(x).
Si trova |
f(g(x)) = f(g(x0)) + f′(g(x
0))g′(x
0)(x −x0)
+ f′(y
0) o(x −x0) + o(y −y0) .
|
E’
lim x→x0 o(y −y0)
x −x0 = lim x→x0 o(y −y0)
y −y0 y −y0
x −x0 = 0.
Dunque, la parentesi graffa è o(x − x0)
e la prima formula degli incrementi finiti vale in
x0 per
f(g(x)), con
coeffciente
f′(g(x
0))g′(x
0),
che è quindi la derivata della funzione composta:
Dx0f(g(x)) = f′(g(x
0))g′(x
0).
Esempio 97 Ricordiamo che
Dx0 1
x = − 1
x02.
Consideriamo ora h(x) = 1∕x
e una generica funzione g(x)
derivabile e non nulla in x0.
Sia ϕ(x) = h(g(x)) = 1∕g(x).
La formula di derivazione della funzione composta dà:
Dx0 1
g(x) = − 1
g2(x0)g′(x
0). ■
Combinando il caso visto nell’Esempio 97 con la formula di derivazione del
prodotto si trova:
Dx0f(x)
g(x) = f′(x
0)g(x0) − f(x0)g′(x
0)
g2(x0) .
Si usi questa formula per provare che
D tan x = 1
cos 2x = 1 + tan 2x
e si calcoli la formula analoga per cot x
e per le corrispondenti funzioni iperboliche.
Esempio 98 Si sa, dalla tabella 2.4, che
d
dx log |x| = 1
x
(ovviamente se x≠0).
Dunque, se f(x)
è derivabile e non nulla,
d
dx log |f(x)| = f′(x)
f(x) .
Applicando questa formula alla funzione
f(x) = tan x
si trova
d
dx log | tan(x∕2)| = 1
sin x.
Ovviamente questa formula vale se x≠kπ + π∕2,
perchè in questi punti tan x
non è definita, e se x≠kπ
perché in tali punti si annulla la derivata. Ricordando che
cos x = sin(x + π)
si trovi una funzione la cui derivata è
1∕ cos x.
Queste formule sono utili nel calcolo delle
primitive. ■
Derivata della funzione inversa La regola per il calcolo della derivata della funzione
inversa è più complicata e richiede un’ipotesi in più: si deve avere una funzione
f(x) iniettiva e continua
su un intervallo (a,b).
Inoltre, la funzione deve essere derivabile in
x0 ∈ (a,b) e deve
essere f′(x
0)≠0. Sia
f−1(y) la funzione
inversa di f(x)
e sia y0 = f(x0).
Sotto queste condizioni vale la formula:
Dy0f−1(y) = 1
f′(x0),y0 = f(x0) ossiax0 = f−1(y
0).
Limitiamoci ad illustrare geometricamente questa formula. Ricordiamo che il grafico
di una funzione e della sua funzione inversa devono partire ambedue dall’asse delle
ascisse e che l’uno è il simmetrico dell’altro rispetto alla prima bisettrice.
Le tangenti, quindi, sono simmetriche rispetto alla prima bisettrice. Sia
y = y0 + m(x − x0) una retta
passante per (x0,y0).
La sua simmetrica rispetto alla prima bisettrice ha coeffciente angolare
1∕m. E
ora ricordiamo che il coeffciente angolare della tangente, quando essa non è
verticale, è la derivata della funzione nel punto che stiamo considerando. Questi
argomenti sono illustrati in figure 3.3.
Vediamo come si usa questa regola per calcolare la derivata della funzione
arctan x, funzione inversa
della restrizione a (−π∕2,π∕2)
della funzione tan x.
E’:
D tan x = 1 + tan 2x.
Se y0 = tan x0, la
derivata di arctan x
in y0
è
1
Dx0 tan x = 1
1 + tan 2x0 = 1
1 + y02.
La tabella 3.1 riassume le regole di derivazione ed elenca le derivate principali che
vanno ricordate. Le regole di calcolo sono state appena dimostrate mentre le
formule delle derivate fondamentali si deducono dai limiti notevoli, combinati con le
regole di calcolo. Notiamo che la tabella non riporta una formula per la derivata di
f(x)g(x),
perché invece di ricordare questa formula conviene notare che
f(x)g(x) = eg(x) log f(x).
La derivata dell’espressione a destra si calcola semplicemente usando la regola di
derivazione delle funzioni composte e quella del prodotto.
Table 3.1: Derivate fondamentali e regole di calcolo
funzioni
derivata
Dx0(hf(x) + kg(x))
hf′(x
0) + kg′(x
0)
Dx0f(x)g(x)
f′(x
0)g(x0) + f(x0)g′(x
0)
Dx0f(g(x))
f′(g(x
0))g′(x
0)
Dy0f−1(x)
1
f′(f−1(y
0))
Dx0f(x)
g(x)
f′(x
0)g(x0) − f(x0)g′(x
0)
g2(x
0)
Dx0 log |f(x)|
f′(x
0)
f(x0)
funzione
derivata
xa
axa−1
Dx0|x|
x0
|x0|
sin x
cos x
cos x
− sin x
tan x
1
cos 2x = 1 + tan 2x
cot x
−1
sin 2x = −1 − cot 2x
funzione
derivata
arcsin x
1
1−x2
arccos x
− 1
1−x2
arctan x
1
1+x2
arccotanx
− 1
1+x2
ex
ex
log |x|
1∕x
sinh x
cosh x
cosh x
sinh x
tanh x
1
cosh 2x = 1 − tanh 2x
sett shx
1
1+x2
sett chx
1
x2 −1
sett thx
1
x2 −1
sett thx
1
1−x2
sett cthx
1
1−x2
3.4 Notazioni usate nei corsi di fisica
Nei corsi di fisica, e in generale nei corsi a carattere più applicativo, sembra a
prima vista che le notazioni sulle derivate vengano usate in modo alquanto “libero”.
Per esempio, si trova che
df
dx = gviene scrittodf = gdx.
In realtà non si tratta di abusi, ma questi procedimenti tengono nascosti
alcuni passaggi che è bene chiarire. Prima di tutto va detto che il simbolo
d in
questo contesto viene usato per indicare la derivata, al posto del simbolo
D (cosa che noi
faremo al Cap. 4, nel contesto della ricerca delle primitive). Nelle applicazioni, si sottintende
il fatto che la x
è a sua volta funzione di una ulteriore variabile, diciamo
t, che
non viene indicata. Allora,
df = df(x(t))
dt = f′(x(t))x′(t) = g(t)x′(t)
che, con la notazione d per indicare
la derivata e sottintendendo
la variabile t,
si scrive appunto
df = gdx.
Un (apparente) abuso di notazioni analogo si incontra anche
nell’uso del differenziale. Ricordiamo che il differenziale di
f(x) in
x0 è la
trasformazione
h↦f′(x
0)h.
Questa trasformazione si indica anche col simbolo
df:
df(x0)h = f′(x
0)h.
Nel caso particolare della funzione g(x) = x
la sua trasformazione differenziale è
dx = h
e ciò suggerisce di scrivere la trasformazione differenziale di
f
come
dfdx
(ossia, df(x0)dx = f′(x
0)dx = f′(x
0)h, ma
usualmente x0
si sottintende). L’utilità di questa notazione dipende ancora dal fatto che in fisica
x è funzione di una
sottintesa variabile t
e quindi
dfdx = f′(x(t))x′(t)dt
è un modo veloce di scrivere il differenziale della funzione composta. Ulteriori apparenti abusi
di notazione,
analoghi ai precedenti, si incontrano quando si devono usare funzioni di
più variabili, e verranno spiegati al paragrafo 8.4 e nel corso di Analisi
Matematica 2.
3.5 Derivate ed ordine dei numeri reali
Sia f(x) una funzione
derivabile su (a,b).
La relazione di ordine dei numeri reali conduce alla definizione di funzione monotona e,
per mezzo della regola dei segni del prodotto, alla definizione di funzioni pari e
dispari.
Ricordiamo che f(x)
è crescente su (a,b)
quando
f(x) − f(x0)
x − x0 ≥ 0∀x,x0 ∈ (a,b)x≠x0.
Passando al limite per x → x0
si trova che f′(x
0) ≥ 0 e ciò
vale per ogni x0 ∈ (a,b).
Trattando in modo analogo le funzioni decrescenti si trova:
Teorema 99 Se f(x)
è derivabile e crescente (non necessariamente in senso stretto) su
(a,b)
allora f′(x) ≥ 0
per ogni x ∈ (a,b);
Se f(x)
è derivabile e decrescente (non necessariamente in senso stretto) su
(a,b)
allora f′(x) ≤ 0
per ogni x ∈ (a,b).
Osservazione 100 E’ opportuno notare gli esempi seguenti:
Il problema della relazione tra derivata e monotonia verrà ripreso
al Cap. 4. Consideriamo ora la relazione tra parità e derivata. Sia
f(x) derivabile
si (−a,a).
Vale: |
la funzione è pari se f(x) = f(−x);
la funzione è dispari se f(x) = −f(−x).
|
Derivando i due membri mediante il teorema della funzione composta si trova
|
se la funzione è pari: f′(x) = −f′(−x);
se la funzione è dispari: f′(x) = f′(−x).
|
Dunque si ha:
Teorema 101 Sia f(x) ∈ C∞(ℝ).
Se f(x)
è pari oppure dispari, le sue derivate di ordine pari hanno la stessa parità di
f(x),
quelle di ordine dispari hanno parità opposta.
Una funzione dispari deve annullarsi in
x0 = 0. Vale
quindi:
Teorema 102 La derivata in x0 = 0
di una funzione pari è nulla e quindi se
f(x) ∈ C∞(ℝ)
è pari tutte le sue derivate di ordine dispari sono nulle in
x0 = 0;
se f(x)
è dispari tutte le sue derivate di ordine pari sono nulle in
x0.
E’ interessante vedere l’interpretazione geometrica del Teorema 101 notando
che le secanti in punti corrispondenti del grafico sono parallele, e quindi hanno
la stessa pendenza, nel caso di funzioni dispari; hanno pendenza opposta nel
caso di funzioni pari, come illustrato nella figura 3.5. Tale relazione si conserva
passando al limite dei rapporti incrementali, ossia si conserva per le derivate.
3.5.1 Il teorema di Fermat ed i punti di estremo
Consideriamo una funzione f(x)
definita su un intervallo (a,b) e
sia x0 ∈ (a,b). punto importante
da sottolineare: x0
è interno all’intervallo. NON è uno degli estremi. Vale il teorema
seguente:
Teorema 103 (di Fermat) Se:
- f(x)
è definita in (a,b);
- x0 ∈ (a,b)
è punto di massimo oppure di minimo locale di
f(x)
- la funzione f(x)
è derivabile in x0,
allora f′(x
0) = 0.
Dim. Per assurdo, sia
f′(x
0) > 0,f′(x
0) = lim h→0f(x0 + h) − f(x0)
h .
Il teorema di permanenza del segno asserisce che esiste
δ > 0 tale
che
−δ < h < δ⇒f(x0 + h) − f(x0)
h > 0,
ossia,
f(x0 + h) − f(x0) ed h hanno segno concorde.
Dunque, se h > 0
vale f(x0 + h) > f(x0)
mentre se h < 0
vale f(x0 + h) < f(x0) e
quindi f(x0)
non è né punto di massimo né punto di minimo di
f(x). Il caso
f′(x
0) < 0 si tratta in
modo analogo. ■
L’interpretazione geometrica di questo teorema: ricordiamo che
f′(x
0)
è la pendenza della tangente al grafico della funzione nel punto
(x0,f(x0)). Dunque, se esiste la
tangente al grafico di f(x)
in (x0,f(x0)) ed
x0 è
un punto di massimo o di minimo INTERNO AL DOMINIO DELLA
FUNZIONE, la tangente è orizzontale.
Osservazione 104 Il teorema di Fermat NON
si applica alle derivate direzionali. La funzione
f(x) = 1 − x2,
definita su [−1, 1],
ha minimo nei punti −1
e +1.
Le derivate direzionali in tali punti non sono nulle; anzi sono
+∞
e −∞.
La funzione f(x) = x
definita su [0, 1]
ha minimo in x = 0
e massimo in x = 1.
Le derivate direzionali in ambedue questi punti valgono
1. ■
Il teorema di Fermat ha questa conseguenza importante:
i punti di massimo e di minimo relativo di una funzione vanno cercati
tra i punti nei quali la derivata prima non esiste; i punti nei quali la
derivata prima si annulla e, se ivi definita, gli estremi del dominio della
funzione.
Vediamo alcuni esempi:
Esempio 105 Sia f(x) = |x|,
definita su [−1, 1].
La funzione non è derivabile in x = 0
e, dove derivabile, ha derivata
f′(x) = + 1 sex > 0
− 1 sex < 0.
Dunque, f′(x)
non si annulla mai. Quindi, i punti di massimo e di minimo vanno ricercati tra i
punti −1,
0,
+1 . Sia
invece f(x) = x2,
f′(x) = 2x, definita su
ℝ. La derivata si
annulla nel solo punto x = 0
e quindi la funzione ha al più un solo punto o di massimo o di minimo, nel punto
x = 0. Nel caso
specifico x = 0
è punto di minimo ma questo non si deduce dall’annularsi della derivata
prima. Infatti:
- la funzione f(x) = −x2
ha nulla la derivata nel solo punto
x = 0
che però ora è un punto di massimo;
- Non è detto che la condizione f′(x
0) = 0
implichi che x0
è punto di massimo o di minimo. Per esempio la funzione
f(x) = x3,
definita su ℝ,
ha derivata f′(x) = 3x2,
nulla per x = 0.
Il punto x = 0
non è né punto di massimo né punto di minimo di
f(x)
perché x3 < 0
per x < 0
mentre x3 > 0
per x > 0. ■
I punti nei quali si annulla la derivata prima si chiamano punti estremali oppure
punti stazionari oppure punti critici della funzione. Il teorema di Fermat asserisce
che i punti di massimo o di minimo (assoluto o relativo) di una funzione sono punti
estremali quando: 1) sono punti interni al dominio; 2) la funzione è derivabile in
tali punti.
3.6 Osservazione finale ed importante
Si è insistito sul fatto che la derivata si definisce nei punti interni. Quindi, quando si afferma
l’esistenza di f′(x
0)
implicitamente si afferma anche che la funzione
f(x) è definita in un
intorno di x0 ed inoltre, dal
teorema 91, la funzione f(x)
è continua in x0.
Potrebbe essere discontinua in ogni altro punto. Vediamo la conseguenza
di queste osservazioni sulle derivate successive. Affermando che esiste
f″(x0) implicitamente si
afferma che esiste f′(x) e
quindi anche f(x) in un
intorno di x0. La funzione
f′(x) deve essere continua
in x0 per il teorema 91.
L’esistenza di f′(x) in ogni
punto di un intorno di x0
implica che f(x)
è continua in tale intorno. Queste osservazioni si ripetono per le derivate successive: se
esiste f(n)(x
0) allora
f(n−1)(x
0) è definita in un
intorno di x0 (ed
è continua in x0);
tutte le derivate precedenti sono definite e continue in tale intorno.
3.7 Alcuni esercizi
-
- Un punto materiale si muove con velocità costante di
0, 1
m∕ sec.
Calcolarne la velocità in centimetri al secondo.
- Un punto materiale si muove con accelerazione costante di
0, 01
m∕ sec2.
Calcolarne l’accelerazione in centimetri al secondo per secondo.
- la legge del moto del punto suddetto è
x(t)
quando le lunghezze si misurano in metri e
ξ(t)
quando si misurano in centimetri. E’ quindi
ξ(t) = 100x(t).
Ritrovare i risultati precedenti sulla velocità e accelerazione
usando linearità della derivata.
-
- Un punto materiale si muove con velocità costante di
0, 1
m∕ sec.
Calcolarne la velocità in metri al minuto.
- Un punto materiale si muove con accelerazione costante di
0, 01
m∕ sec2.
Calcolarne l’accelerazione in metri al minuto per minuto.
- la legge del moto del punto suddetto è
x(t)
quando il tempo si misura in secondi e
ξ(τ)
quando il tempo si misura in minuti. E’ quindi
ξ(τ) = x(60τ).
Ritrovare i risultati precedenti sulla velocità e accelerazione
usando la regola di derivazione della funzione composta.
- Le regole di derivazione mostrano che per ogni numero reale
a
vale
d
dx sin ax = a cos ax, d
dxeax = aeax
e simili. Invece,
d
dx log ax = 1
x
(si ha qui a > 0
ed x > 0).
Dunque, in questo caso il fattore moltiplicativo
a
“non ha effetto” sul calcolo della derivata. Spiegare il motivo usando le regole
di calcolo dei logaritmi.
- Sia f(x)
una funzione derivabile. Dare condizioni per la derivabilità di
|f(x)| in
x0, sia quando
f(x0)≠0 che quando
f(x0) = 0. Ha qualche
interesse sapere se x0
è nullo?
- Si è visto che che se f(x) è
pari e derivabile allora f′(x)
è dispari; se f(x) è dispari
e derivabile allora f′(x)
è pari. Si illustri il significato di questa proprietà tracciando i grafici di due
funzioni, una pari e una dispari, e disegnando alcune tangenti. Ossia, si
considerino le figure 3.7 in alcuni casi concreti.
- (⋆) Si mostri che
se f(x) è una funzione
derivabile per cui f(x) = f(1∕x)
allora f′(x)
verifica
se g(x) è una funzione
derivabile per cui g(x) = −g(−1∕x)
allora g′(x)
verifica
Si verifichi che le funzioni
f(x) = (1 + x) 1 + 1
x,g(x) = (1 + x) 1
x − 1
hanno le proprietà richieste e si verifichi che le loro derivate effettivamente
soddisfano le (3.3) e (3.4).
- (⋆)
Sia
f(x) = x2 sex ∈ ℚ
x sex∉ℚ
Dire se esitono punti in cui la funzione è continua e punti in cui è
derivabile.
- (⋆)
Sia
f(x) = x2 sex ∈ ℚ
x3 sex∉ℚ
Dire se esitono punti in cui la funzione è continua e punti in cui è
derivabile.
- (⋆)
Sia
f(x) = x2 sex ∈ ℚ
x4 sex∉ℚ
Dire se esitono punti in cui la funzione è continua e punti in cui è
derivabile.
- (⋆) Costruire
una funzione f(x)
con queste proprietà:
- è continua in x0 = 0
- per x → 0
vale f = o(x5)
- la funzione non ha derivata seconda in
x0 = 0.
- (⋆)
Sia
f(x) = x3 sin 1∕x sex≠0
0 sex = 0.
Si mostri che f(x)
è di classe C1
su ℝ e che
per x → 0 si ha
f = o(x2). Dire se è
vero che f′(x) = o(x)
(per x → 0).
- Sia
f(x) = x + x2 sin(1∕x) sex≠0,f(0) = 0.
Mostrare che f′(0) = 1 ma che
non esistono intorni di 0
su cui f(x)
è crescente. Si studi la derivabilità della funzione anche per
x≠0.
- Sia
f(x) = x sex ∈ ℚ,f(x) = sin x sex∉ℚ.
Mostrare che f′(0) = 1 ma che
non esistono intorni di 0
su cui f(x)
è crescente. Si studi la derivabilità della funzione anche per
x≠0.
- (⋆) si costruisca una
funzione di classe C1(ℝ)
con queste proprietà:
- la funzione è dispari ed f(x) ≤ 0
per x < 0
(e quindi f(x) ≥ 0
per x > 0
ed f(0) = 0);
- la tangente a grafico nel punto
(0,f(0)) = (0, 0)
è orizzontale;
- il punto x0 = 0
non è punto di flesso a tangente orizzontale per la funzione
f(x).
- Si consideri la parabola y = x2.
Se ne calcoli la tangente nel punto di coordinate
(x0,x02) e si
mostri che tale retta tangente biseca il segmento congiungente il vertice della parabola
col punto (x0, 0).
- Si consideri l’iperbole y = 1∕x
e per ogni x0 > 0 se ne calcoli
la tangente nel punto (x0, 1∕x0).
Si calcoli l’area del triangolo che ha per vertici l’origine e le intersezioni di tale
tangente con gli assi coordinati. Si mostri che l’area del triangolo non dipende da
x0.
- Sia f(x) = x2.
Si considerino i due punti del grafico di
f(x),
(x0,x02) ed
(x1,x12).
Si calcolino le tangenti al grafico in tali punti e si calcoli l’ascissa del
loro punto comune. Si noti che tale ascissa è la media aritmetica
(x0 + x1)∕2 dei due
numeri x0
ed x1.
- Sia f(x) = x.
Si considerino i due punti del grafico di
f(x),
(x0,x0) ed
(x1,x1).
Si calcolino le tangenti al grafico in tali punti e si calcoli l’ascissa del
loro punto comune. Si noti che tale ascissa è la media geometrica
x0 x1 dei due
numeri x0
ed x1.
- Elevando al quadrato ambedue i membri membri, si provi che vale la
disuguaglianza
x
1x2 ≤x1 + x2
2
ossia, la media geometrica è minore della media aritmetica. Si usino le
osservazioni agli esercizi 17 e 18. Si traccino i grafici delle due funzioni
f(x) = x2 ed
f(x) = x
e si interpreti la disuguaglianza precedente mediante le ascisse dei punti di
intersezione delle tangenti ai due grafici.
Capitolo 4
Funzioni: proprietà globali
Niente la soddisfa mai, eccetto le dimostrazioni; le teorie non
dimostrate non fanno per lei, non le accetta. E’ questo lo
spirito giusto, lo ammetto: mi attrae, ne sento l’influenza; se
stessi di più con lei, penso che l’adotterei anch’io. Diario di
Adamo, Il diario di Adamo ed Eva di Mark Twain
fino ad ora abbiamo studiato le proprietà “locali” delle funzioni, che
dipendono solamente dal comportamento della funzione in un intorno del punto
x0. Ora
invece studiamo le proprietà delle funzioni in relazione a tutto il loro dominio, che
frequentemente (ma non sempre) sarà un intervallo.
4.1 Teorema delle funzioni monotone
La definizione di limite permette solamente di verificare che il limite è
effettivamente ciò che l’intuizione ci ha suggerito. In particolare, non asserisce che
un limite debba esistere o meno. Un teorema che asserisce l’esistenza del limite, e ne
indica il valore, è il seguente, che si chiama teorema delle funzioni monotone Lo
enunciamo nel caso delle funzioni crescenti, lasciando per esercizio di adattare
l’asserto al caso delle funzioni decrescenti.
Teorema 106 Sia f(x)
una funzione crescente (anche non strettamente). Si ha:
Notiamo che il segno di disuguaglianza è stato
scritto in colore, per sottolineare che le disuguaglianze
sono strette. Anche se la funzione è definita in
x0,
il valore che essa prende in x0
non compare nell’enunciato del teorema.
Prima di provare il teorema, vediamone alcune conseguenze.
La dimostrazione del teorema delle funzioni monotone
Proviamo il teorema per i limiti sinistri di funzioni crescenti. Inoltre, studiamo il caso
x0 < +∞ lasciando per
esercizio il caso in cui x0 = +∞.
Conviene distinguere due casi:
Caso 1: sup{f(x)|x < x0} = +∞
, ossia f(x)
superiormente illimitata Come si è notato, in questo caso
x0 è
l’estremo destro del dominio della funzione e bisogna provare
lim x→x0−f(x) = +∞.
Dunque vanno considerate le disequazioni
f(x) > 𝜖
e va provato che ciascuna di esse è soddisfatta in un intervallo
(c,x0), con
c = c𝜖 < x0.
Essendo la funzione superiormente illimitata, esiste un particolare
x𝜖 tale
che
f(x𝜖) > 𝜖.
La funzione è crescente e quindi per
x ∈ (x𝜖,x0) si
ha
f(x) ≥ f(x𝜖) > 𝜖.
Dunque, si può scegliere c𝜖 = x𝜖.
Caso 2: sup{f(x)|x < x0} = l < +∞
In questo caso va provato
lim x→x0−f(x) = l
e quindi vanno considerate le disequazioni
l − 𝜖 < f(x) < l + 𝜖.
Va mostrato che ciascuna di esse è soddisfatta in un intervallo
(c𝜖,x0).
La definizione di estremo superiore mostra che esiste
x𝜖 per
cui
l − 𝜖 < f(x𝜖).
La funzione è crescente e quindi
x ∈ (x𝜖,x0)⇒f(x𝜖) ≤ f(x) ≤ l.
L’ultima disuguaglianza discende dalla definizione di
l. L’asserto segue scegliendo
c𝜖 = x𝜖. ■
Ripetiamo che il teorema delle funzioni monotone non richiede che
il dominio sia un intervallo. Esso vale per funzioni definite su un
qualsiasi insieme, purché i limiti da destra e/o da sinistra possano
studiarsi. In particolare, vale per le successioni. Nel caso delle
successioni, il teorema delle funzioni monotone può enunciarsi come segue:
Teorema 107 Se {xn}
è una successione monotona, essa ammette limite per
n → +∞,
finito o meno, e vale:
- se la successione è crescente allora
lim xn = sup{xn,n ∈ ℕ};
- se la successione è decrescente allora
lim xn = inf{xn,n ∈ ℕ}.
Prendiamo l’occasione offerta dal Teorema 107 per introdurre
un nuovo termine: una successione che ammette limite per
n → +∞, finito
oppure +∞
oppure −∞,
si chiama successione regolare Se il limite è finito la successione è una
successione convergente
Si noti che la dimostrazione del Teorema delle funzioni monotone usa
la completezza dei numeri reali, ossia la proprietà di Dedekind.
4.2 Il Teorema di Bolzano-Weierstrass
Ricordiamo che si chiama successione convergente una successione che ammette
limite finito. Il teorema seguente è importante in moltissime applicazioni:
Teorema 108 (di Bolzano-Weierstrass) Ogni successione limitata
ammette sottosuccessioni convergenti, ossia dotate di limite finito.
Dim. Indichiamo con m l’estremo
inferiore dell’immagine {xn}
della successione,
m = inf{xn}.
Ora procediamo in modo iterativo:
-
Passo 1:
- Sia S1 = {xn},
l’immagine della successione e sia
c1 = sup S1.
Ovviamente, c1 ≥ m.
Scegliamo un qualsiasi xn1
tale che
c1 − 1 < xn1 ≤ c1.
L’indice n1
esiste per la definizione di estremo superiore.
-
Passo 2:
- Definiamo
S2 = {xn,|n > n1},c2 = sup S2.
Ovviamente, S2 ⊆ S1
e quindi m ≤ c2 ≤ c1.
Scegliamo xn2
tale che
c2 −1
2 < xn2 ≤ c2.
E’:
n2 > n1.
-
Passo 3:
- Definiamo
S3 = {xn,|n > n2},c3 = sup S3.
Ovviamente, S3 ⊆ S2
e quindi m ≤ c3 ≤ c2.
Scegliamo xn3
tale che
c3 −1
3 < xn3 ≤ c3.
E’:
n3 > n2.
-
Passo k:
- Definiamo
Sk = {xn,|n > nk−1},ck = sup Sk.
Ovviamente, Sk ⊆ Sk−1
e quindi m ≤ ck ≤ ck−1.
Scegliamo xnk
tale che
e si ha
In questo modo abbiamo costruito due successioni:
- la successione {ck}
decrescente ed inferiormente limitata, e quindi dotata di limite finito
l:
lim ck = l ∈ ℝ.
- la sottosuccessione {xnk}
della successione {xn}.
Si noti che {xnk}
è effettivamente una sottosuccessione, perché
{nk}
è crescente, si veda la (4.2).
La (4.1) mostra che {xnk} ammette
limite, uguale a quello di {ck},
e quindi finito. Ciò è quanto volevamo provare.
■
Si noti che la dimostrazione del Teorema di Bolzano-Weierstrass usa
il Teorema delle funzioni monotone e quindi usa la completezza dei
numeri reali .
4.3 Il teorema di Weierstrass
Notiamo che esistono funzioni continue prive di punti di massimo e di minimo. Sono esempi le
funzioni arctan x, definita
su ℝ, la funzione
f(x) = 1∕x definita su
(0, +∞) ma anche la
funzione f(x) = 1∕x definita
su (0, 1], che ammette
punto di minimo (x = 1)
ma non punto di massimo. In questi esempi le funzioni sono continue su intervalli
che non sono chiusi oppure non sono limitati. Invece:
Teorema 109 (di Weierstrass) Sia
f(x) definita su un intervallo
limitato e chiuso [a,b].
Supponiamo inoltre che f(x)
sia continua su [a,b].
L’immagine della funzione ammette sia massimo che minimo e quindi esistono
x0 ed
x1 in
[a,b] tali
che: |
x0 è punto di massimo ossia f(x0) = max{f(x),x ∈ [a,b]};
x1 è punto di minimo ossia f(x1) = min{f(x),x ∈ [a,b]}.
|
Il teorema non afferma l’unicità dei punti di massimo o di minimo. E’ importante
notare che questo teorema si può riadattare per dimostrare l’esistenza di punti di
massimo e/o di minimo anche in casi in cui le ipotesi non sono soddisfatte.
Consideriamo l’esempio seguente:
Esempio 110
In modo analogo si provi che se f(x)
è definita su (a,b)
e se
lim x→af(x) = lim x→bf(x) = +∞
allora la funzione ammette punti di minimo
(assoluti). ■
Supponiamo che la funzione f(x)
sia continua su ℝ
e verifichi |
lim x→−∞f(x) = lim x→+∞f(x) = c.
| (4.3) |
Esista un punto x0
tale che d = f(x0) > c.
Allora, la funzione ammette punto di massimo. Infatti, sia
𝜖 = (d − c)∕2. Per definizione
di limite, esiste R > 0
tale che
|x| > R⇒f(x) < c + d − c
2 = d + c
2 < d.
Dunque, se |x| > R vale
f(x) < d = f(x0). Aumentando il
valore di R, si può
anche avere |x0| < R. La
funzione f(x) è continua
in particolare su [−R,R],
intervallo limitato e chiuso, e quindi ammette ivi un punto di massimo
x1:
f(x1) ≥ f(x)∀x ∈ [−R,R].
In tale punto si ha
f(x1) ≥ f(x0) = d
più grande di f(x)
sia se |x| > R
che se |x|≤ R.
Questo caso è illustrato nei grafici della figura 4.2. Si noti che il grafico a sinistra
mostra anche l’esistenza di un punto di minimo, che però non è conseguenza
della proprietà (4.3). Infatti, la funzione a destra non ha punti di minimo.
In modo analogo si provi che se f(x)
è definita su (a,b)
e se
lim x→af(x) = lim x→bf(x) = +∞
allora la funzione ammette punti di minimo
(assoluti). ■
4.3.1 La dimostrazione del Teorema di Weierstrass
Premessa: nella dimostrazione useremo il Teorema di Bolzano Weierstrass e le
proprietà seguenti:
-
A)
- se {xn}
è una successione a valori in [a,b],
ossia se a ≤ xn ≤ b,
e se esiste lim xn = x0,
allora
si ha anche a ≤ x0 ≤ b.
-
B)
- se f(x)
è continua in x0
e se xn → x0
allora
f(xn) → f(x0)
(naturalmente si suppone xn ∈ domf(x)).
-
C)
- se una successione converge, ogni sua sottosuccessione converge, ed ha
il medesimo limite, finito o meno (Teorema 83). Applicheremo questo
teorema ad una successione {f(xn)}.
Non sapremo che {xn}
converge, ma sapremo che f(xn) → L.
Se {xnk}
è una sottosuccessione di {xn}
allora {f(xnk)}
è sottosuccessione di {f(xn)}
e quindi f(xnk) → L.
Proviamo ora il teorema di Weierstrass. Proviamo l’esistenza dei punti di massimo (la
dimostrazione dell’esistenza di punti di minimo è analoga). La dimostrazione è in
tre passi:
Passo 1: la costruzione di una successione massimizzante
Si chiama successione massimizzante per una funzione
f(x) definita su un
insieme D una
successione {xn}
con xn ∈ domf(x) per
ogni n,
e tale che inoltre
lim f(xn) = sup{f(x),x ∈ D}.
L’estremo superiore può essere finito o meno, e la successione
{xn}
generalmente non è regolare. Una successione massimizzante
esiste sempre, senza alcuna condizione né sulla funzione
f(x) né
sul suo dominio. Infatti, sia
L = sup A,A = imf(x) = {f(x),x ∈ D}.
Sia nel caso L = +∞ che
nel caso L ∈ ℝ, esiste
una successione {yn}
di punti di A che
converge ad L. I punti
di A sono valori della
funzione f(x) e quindi
esiste una successione {xn}
tale che f(xn) = yn.
Dunque,
lim f(xn) = L.
Passo 2: se domf(x) = [a,b]
allora esiste una successione massimizzante per
f(x) che è anche
convergente.Sia {xn}
la successione massimizzante costruita al passo 1. Si ha:
a ≤ xn ≤ b.
E quindi la successione {xn}
è limitata. Per il Teorema di Bolzano-Weierstrass, essa ammette almeno una sottosuccessione
{xnk}
convergente:
lim xnk = x0.
Per la proprietà A), il punto x0
appartiene all’intervallo chiuso [a,b].
Inoltre, {f(xnk)}
è sottosuccessione della successione convergente
{f(xn)} e
quindi ha lo
stesso limite L:
lim f(xnk) = L.
Paso 3: se f(x) è
continua, il punto x0 è
punto di massimo per f(x)Sia
x0 = lim xnk il numero costruito al
Passo 2. Si è notato
che x0 ∈ [a,b]
e quindi è un punto del dominio della funzione continua
f(x).
Dunque
si ha:
f(x0) = lim f(xnk) = L = sup{f(x),x ∈ [a,b]}.
Ossia, l’immagine della funzione ammette massimo ed
x0 è
punto di massimo. Ciò completa la dimostrazione
Il teorema di Weierstrass dipende dal teorema di Bolzano-Weierstrass
e quindi usa la proprietà di completezza dei numeri reali.
4.4 Teorema dei valori intermedi
Questo teorema afferma che, sotto certe ipotesi, esistono soluzioni dell’equazione
f(x) = c.
Essenzialmente, le ipotesi sono che 1)
f(x) sia continua e 2)
che il grafico di f(x)
“tagli quota c”.
Dunque, il contenuto di questi teoremi sembra intuitivo, ma non è per niente
così. Infatti, si consideri l’equazione
x3 = 2.
Per provare l’esistenza di soluzioni, si può ragionare così: la funzione
f(x) = x3 vale
−8 per
x = −2 e vale
+8 per
x = +2. Inoltre
è continua. Quindi, il suo grafico “non fa salti” e da qualche parte deve tagliare la
retta y = 2;
ossia l’equazione ammette almeno una soluzione. Questo discorso, dall’apparenza
convincente, è sostanzialmente falso: pensiamo di lavorare con valori di
x solamente razionali. Le
condizioni su f(x) dette sopra
valgono in ℚ, ma nessun
numero razionale verifica x3 = 2.
Dunque, il ragionamento è sbagliato. Proviamo però che l’asserto vale se si lavora in
ℝ. Ricordiamo la
differenza essenziale tra ℚ
e ℝ: in
ℝ vale
la proprietà di Dedekind: ogni insieme superiormente limitato ammette
estremo superiore; ogni insieme inferiormente limitato ammette estremo inferiore.
E’ grazie alla proprietà di Dedekind che si può provare il risultato seguente:
Teorema 111 Sia f(x)
continua su [a,b].
Si consideri l’equazione |
f(x) = c,x ∈ [a,b] ⊆ ℝ.
| (4.4) |
Quest’equazione ammette almeno una soluzione se
c è compreso
tra f(a) ed
f(b).
Il teorema non asserisce l’unicità della soluzione. Prima di provare il teorema,
premettiamo vari commenti. Ricordiamo ora che, Il Teorema di Weierstrass
asserisce l’esistenza di punti di massimo e di minimo della funzione
f(x) in
[a,b] se essa è continua
sull’intervallo [a,b].
Esistono cioè x0
ed x1 in
[a,b] tali
che
f(x0) = min x∈[a,b]f(x),f(x1) = max x∈[a,b]f(x).
Il Teorema 111 vale anche sull’intervallo di estremi
x0 ed
x1 e
quindi si può enunciare:
Teorema 112 Una funzione continua su un intervallo limitato e chiuso
prende tutti i valori compresi tra il suo minimo e il suo massimo.
L’asserto dei due teoremi 111 e 112 si chiama teorema dei
valori intermedi La versione del teorema che si ottiene quando
f(a)f(b) < 0 e si
sceglie c = 0 si
chiama teorema di esistenza degli zeri
Teorema 113 (di esistenza degli zeri) Una funzione f(x)
continua su [a,b]
e che ivi prende sia valori positivi che valori negativi, si annulla almeno in un
punto di [a,b].
Il teorema dei valori intermedi dipende dalla proprietà di completezza
dei numeri reali, e richiede in modo essenziale che il dominio della
funzione sia un intervallo.
Dimostrato il teorema dei valori intermedi, possiamo anche estendere in vari
modi le considerazioni da cui siamo partiti. Per esempio:
Corollario 114 Se
f(x)
è continua su
ℝ
ed inoltre i due limiti (finiti o meno)
lim x→−∞f(x), lim x→+∞f(x)
hanno segni opposti, la funzione ammette almeno uno zero. In particolare, tutti
i polinomi di grado dispari hanno uno zero in ℝ.
Dim. Infatti, il teorema di permanenza del segno garantisce l’esistenza di
R tale
che
f(−R) ed f(R) hanno segno opposto.
Si applica quindi il teorema 112 all’intervallo
[−R,R]. Questo risultati
si applica in particolare ai polinomi di grado dispari perché essi sono infiniti di segno opposto
per x → +∞ e per
x →−∞. ■
Il Teorema dei valori intermedi mostra che le funzioni continue trasformano
intervalli in intervalli. Più precisamente si ha, usando il Teorema 112:
Corollario 115 Sia J
un intervallo (limitato o meno, chiuso o meno). Se f(x)
è definita e continua su J
allora f(J)
è un intervallo. Se inoltre J
è un intervallo limitato e chiuso, J = [a,b],
allora f(J)
è un intervallo limitato e chiuso contentente l’intervallo [f(a),f(b)].
Si faccia un esempio per mostrare che in generale
f(J) contiene propriamente
l’intervallo [f(a),f(b)].
Interpretiamo ora questi risultati dal punto di vista del grafico di due funzioni:
Corollario 116 Siano
f(x)
e
g(x)
due funzioni continue su
[a,b]
e supponiamo che
f(a) < g(a),f(b) > g(b)
(o viceversa). I grafici delle due funzioni hanno almeno un punto comune.
Dim. I grafici hanno un punto comune quando esiste una soluzione
x ∈ [a,b]
dell’equazione
f(x) = g(x)ossia di f(x) − g(x) = 0.
L’esistenza di (almeno) una soluzione di quest’equazione segue dal Teorema 112,
notando che
f(a) − g(a) < 0,f(b) − g(b) > 0. ■
4.4.1 La dimostrazione del teorema dei valori intermedi
Nella dimostrazione useremo la proprietà seguente, conseguenza del teorema di
permanenza del segno per le funzioni continue: Osservazione: supponiamo che la
funzione f(x) sia
continua su [a,b]
e sia m ∈ (a,b).
Allora si ha:
- se f(x) < c
per x < m
allora f(m) = lim x→m−f(x) ≤ c
(si noti che si è usato la continuità di f(x)
nel punto m).
- sia {xn}
una successione per cui xn > m,
lim xn = m
ed f(xn) ≥ c.
Sempre usando la continuità di f(x)
nel punto m
si ha f(m) = lim f(xn) ≥ c.
Proviamo ora il teorema. Per fissare le idee facciamo la dimostrazione nel caso
f(a) < f(b) e quindi
f(a) ≤ c ≤ f(b). Naturalmente,
se c = f(a)
oppure c = f(b)
l’asserto è provato e quindi consideriamo il caso in cui le disuguaglianze sono
strette:
Consideriamo l’insieme
Sc = {x ∈ [a,b]|f(x) ≥ c}.
L’insieme Sc
è limitato e quindi esiste
m = inf Sc,m ∈ [a,b].
Osserviamo che:
- La funzione f(x)
è continua e quindi, per (4.5) e per il teorema di permanenza del segno, esiste
𝜖 > 0
tale che
|
f(x) < c∀x ∈ [a,a + 𝜖],f(x) > cx ∈ [b − 𝜖,b].
| (4.6) |
E quindi
Sc ⊆ [a + 𝜖,b],ed m < b − 𝜖, ossia a + 𝜖 ≤ m ≤ b − 𝜖.
Il punto da sottolineare è che
m
è interno al dominio della funzione.
- Inoltre si ha:
|
se x < m allora f(x) < c.
| (4.7) |
La proprietà A) dell’Osservazione mostra che
Proviamo ora che f(m) = c,
e quindi che m
è una soluzione (in generale non l’unica) dell’equazione
f(x) = c.
La dimostrazione consistere nel provare che si ha anche
f(m) ≥ c, cosìche dovrà
essere f(m) = c. Notiamo
che m è il massimo
dei minoranti di Sc.
Dunque, per ogni n
esiste xn ∈ Sc
tale che
m ≤ xn ≤ m + 1
n.
Per il teorema del confornto sui limiti,
xn → m. Inoltre,
essendo xn ∈ Sc, si
ha anche f(xn) ≥ c.
La proprietà B) dell’Osservazione mostra che
Confrontando (4.8) and (4.9) si conclude che si ha
f(m) = c.
Ciò prova l’asserto.
4.4.2 Una conseguenza sulle funzioni iniettive
Una funzione strettamente monotona è iniettiva e quindi invertibile. Il contrario
non vale. Si sono visti esempi di funzioni invertibili ma non monotone. Però gli
esempi che abbiamo visto sono
- esempi di funzioni continue ma non definite su un intervallo;
- esempi di funzioni definite su un intervallo ma non continue.
Il teorema seguente mostra la ragione:
Teorema 117 Sia f(x)
una funzione continua su un intervallo [a,b].
Se essa è iniettiva, allora è strettamente monotona.
Dim. L’iniettività implica che f(a)≠f(b).
Consideriamo il caso
f(a) < f(b).
Proviamo che ciò implica che la funzione è strettamente crescente, ossia che per
ogni x1
ed x2 di
[a,b] con
x1 < x2 si
ha
f(x1) < f(x2)
(l’uguaglianza non può aversi perché la funzione è iniettiva). Consideriamo prima di tutto
i tre punti a,
x1 e
b e proviamo
che f(a) < f(x1) < f(b).
Sia per assurdo
f(x1) < f(a) < f(b).
Il teorema dei valori intermedi applicato a
[x1,b] implica
che esiste d ∈ (x1,b)
tale che f(d) = f(a).
Ciò non può darsi perché la funzione è iniettiva. Dunque,
f(a) < f(x1)
e procedendo in modo analogo si vede anche che
f(x1) < f(b).
Sia ora x2 ∈ (x1,b].
Sull’intervallo [x1,b]
si può lavorare come si è fatto prima sull’intervallo
[a,b] e si
trova
f(x1) < f(x2) < f(b).
In definitiva, qualsiasi coppia di punti
x1,
x2 di
[a,b] tali che
x1 < x2 verifica anche
f(x1) < f(x2). E quindi la funzione
è crescente su [a,b].
Il caso f(a) > f(b) si tratta in
modo analogo. ■
4.5 Funzioni derivabili su intervalli
I due teoremi principali che riguardano le funzioni derivabili in tutti i punti di un
intervallo sono il Teorema di Rolle e il Teorema di Lagrange
Teorema 118 (Teorema di Rolle) Sia
f(x) una
funzione con le seguenti proprietà:
- il suo dominio è un intervallo [a,b]
limitato e chiuso;
- è continua nei punti dell’intervallo chiuso [a,b];
- è derivabile nei punti dell’intervallo aperto (a,b);
- vale f(a) = f(b).
Allora, esiste c ∈ (a,b)
tale che f′(c) = 0.
Dim. Se la funzione è costante, la sua derivata è nulla in ogni punto e quindi un qualsiasi punto
di (a,b) può scegliersi
come punto c. Sia
f(x) non costante. La
funzione è continua su [a,b],
limitato e chiuso, e quindi per il Teorema di Weierstrass ammette un punto di minimo
x0 e un punto
di massimo x1
e vale
f(x0)≠f(x1),
perché la funzione non è costante. Dunque non può essere che
x0 ed
x1 siano gli
estremi a e
b dell’intervallo,
perché in tali punti la funzione prende lo stesso valore. Quindi almeno uno dei due punti
x0 oppure
x1 è interno all’intervallo:
si tratta di un punto c
di estremo, interno all’intervallo, e in cui la funzione è
derivabile. In tale punto la derivata è nulla per il Teorema di
Fermat. ■
Esempio 119 Osserviamo che le ipotesi del Teorema di Rolle non possono essere
eliminate, come provano gli esempi seguenti:
- sia f(x)
definita su [0, 1] ∪ [2, 3],
e sia f(x) = x
se x ∈ [0, 1]
ed f(x) = 3 − x
per x ∈ [2, 3]
(si faccia il grafico di questa funzione). La funzione è continua sul suo
dominio e derivabile nei punti interni al suo dominio. Inoltre prende lo
stesso valore nell’estremo sinistro e nell’estremo destro del dominio, che
non è un intervallo. La derivata di f(x)
non si annulla.
- la funzione
f(x) = x per 0 ≤ x < 1, f(1) = 0
non è continua su [0, 1]
ma verifica le altre ipotesi del Teorema di Rolle. La sua derivata non si
annulla.
- la funzione f(x) = |x|
non è derivabile su (−1, 1)
ma verifica le altre ipotesi del Teorema di Rolle su [−1, 1].
In nessuno dei punti in cui esiste, la derivata prima si annulla.
- la funzione f(x) = x,
definita su [−1, 1],
verifica le prime due ipotesi del Teorema di Rolle, ma non la terza. La sua
derivata prima non si annulla. ■
Se si rimuove l’ultima ipotesi del Teorema di Rolle si trova:
Teorema 120 (Teorema di Lagrange) La funzione
f(x)
verifichi le seguenti ipotesi:
- è definita su un intervallo limitato e chiuso [a,b];
- è continua nei punti di [a,b];
- è derivabile nei punti di (a,b).
Allora, esiste c ∈ (a,b)
tale che
f′(c) = f(b) − f(a)
b − a .
Dim. Si noti che
y = f(a) + f(b) − f(a)
b − a (x − a)
è l’equazione della corda che congiunge i punti del grafico
(a,f(a)),(b,f(b)).
Dunque, la funzione
g(x) = f(x) −f(a) + f(b) − f(a)
b − a (x − a)
verifica le tre ipotesi del Teorema di Rolle. Dunque, esiste
c ∈ (a,b) tale
che
g′(c) = 0 ossiaf′(c) = f(b) − f(a)
b − a . ■
Ricordando che f′(c)
è la pendenza della tangente al grafico della funzione in
(c,f(c)) si vede il
significato geometrico del Teorema di Lagrange: esiste un punto del grafico in cui la
tangente al grafico stesso è parallela alla corda congiungente i suoi estremi.
Il punto c
che figura nel Teorema di Lagrange si chiama punto di Lagrange per
f(x) su
(a,b).
Il teorema asserisce l’esistenza, sotto le opportune ipotesi, del punto di
Lagrange ma non l’unicità: potrebbero esistere infiniti punti di Lagrange per
f(x) sull’intervallo
(a,b).
Osservazione 121 Va osservato che:
- il teorema di Rolle implica il Teorema di Lagrange che, a sua volta, si
riduce al Teorema di Rolle se vale f(a) = f(b).
Ossia, i due teoremi sono equivalenti. Usa tenerli distinti solo per
chiarezza di esposizione;
- come nel caso del Teorema di Rolle, nessuna delle ipotesi del Teorema
di Lagrange si può rimuovere.
- se la funzione è derivabile su (a,b),
allora le ipotesi del Teorema di Lagrange valgono su ogni sottointervallo
[x1,x2] di
(a,b), e anzi vale di più:
le ipotesi valgono in [x1,x2]
se f(x) è
derivabile su (a,b),
anche se non è continua negli estremi. Quindi: sia
f(x) derivabile
su (a,b). Per ogni
coppia di punti x1,
x2 di
(a,b) esiste
c
tale che
|
f′(c) = f(x2) − f(x1)
x2 − x1 .
| (4.10) |
Il punto c
dipende sia da x1
che da x2.
- Applicando il teorema di Rolle alla funzione
f(x) − g(x)
si può anche provare la seguente generalizzazione del teorema di Lagrange:
Teorema 122 se le due funzioni sono continue su [a,b]
e derivabili su (a,b)
e se inoltre
f(a) = g(a),f(b) = g(b)
allora esiste c ∈ (a,b)
con questa proprietà: le tangenti ai grafici di f(x)
e g(x)
rispettivamente nei punti (c,f(c))
e (c,g(c))
(con la medesima ascissa c)
sono parallele. Ossia, in tale punto si ha
f′(c) = g′(c).
Si veda la figura 4.3.
La formula (4.10) si chiama seconda formula degli incrementi finiti o anche
formula della media La formula della media si scrive anche |
f(x2) − f(x1) = f′(c)(x
2 − x1)ossia f(x2) = f(x1) + f′(c)(x
2 − x1).
| (4.11) |
4.5.1 Conseguenze del Teorema di Lagrange
Vediamo due conseguenze importanti del Teorema di Lagrange.
Conseguenza 1) Sia f(x)
continua in un intervallo [a,b].
Se f′(x) = 0 in ogni punto
dell’intervallo (a,b),
allora f(x) è costante
su [a,b]. Infatti, si
fissi un punto x0 ∈ (a,b).
Facciamo vedere che in ogni altro punto vale
f(x) = f(x0).
Per questo, basta notare che la (4.11) implica l’esistenza di
c tale
che
f(x) = f(x0) + f′(c)(x − x
0).
L’asserto segue perché f′(c) = 0.
Di conseguenza:
Lemma 123 Siano F(x)
e G(x)
definite sul medesimo intervallo (a,b)
e derivabili in ciascun punto di (a,b).
Se per ogni x ∈ (a,b)
si ha
F′(x) = G′(x)
allora esiste
c ∈ ℝ
tale che
F(x) = G(x) + c.
Dim. Infatti, la funzione F(x) − G(x)
ha derivata nulla su (a,b)
e quindi è costante,
F(x) − G(x) ≡ c. ■
Se F(x) = G(x) + c
con c
costante, si dice che “le due funzioni differiscono per una costante”.
Osservazione 124 L’ipotesi che il dominio delle funzioni sia un intervallo
è essenziale. Per esempio, si considerino le due funzioni F(x)
e G(x)
definite su (−2, 0) ∪ (0, 2)
con F(x) ≡ 0
e invece G(x) = sgnx.
Ambedue le funzioni hanno derivata nulla in tutti i punti del loro dominio, ma
la loro differenza non è costante. Ciò è conseguenza del fatto che i teoremi
di Rolle e di Lagrange valgono solo quando il dominio della funzione è un
intervallo. ■
Conseguenza 2) Se f(x)
è derivabile su (a,b)
e se f′(x) ≥ 0, allora
f(x) è crescente
su (a,b); se
f(x) è derivabile
su (a,b) e
se f′(x) ≤ 0, allora
f(x) è decrescente
su (a,b).
Sia f′(x) ≥ 0
su (a,b). Si
scelgano x1 ed
x2 arbitrari
in (a,b).
La (4.10) mostra che
f(x2) − f(x1)
x2 − x1 = f′(c).
Il punto c
è un opportuno punto, che non è noto; ma comunque
f′(c) ≥ 0:
f(x2) − f(x1)
x2 − x1 ≥ 0.
Poiché ciò vale per ogni coppia di punti
x1 ed
x2 in
(a,b),
segue che la funzione è crescente. In modo analogo si tratta il caso
f′(x) ≤ 0.
Riassumiamo quanto abbiamo detto nel primo enunciato del teorema seguente:
Dim. La prima affermazione è già stata provata. Proviamo la seconda. La funzione è
crescente in (a,x0) ed
essendo continua in x0
si ha
f(x0) ≥ f(x)∀x < x0.
La funzione è decrescente in (x0,b)
ed essendo continua in x0
si ha ancora
f(x0) ≥ f(x)∀x > x0.
In definitiva, f(x0) ≥ f(x)
per ogni x ∈ (a,b),
ossia x0
è punto di massimo. In modo analogo si tratta il caso del
minimo. ■
4.6 Le primitive
Siano F(x) e
f(x) due funzioni definite su
un medesimo intervallo (a,b).
La funzione F(x) si dice
primitiva di f(x) su
(a,b) se è derivabile
in ogni x ∈ (a,b)
e vale
F′(x) = f(x)∀x ∈ (a,b).
Dunque, una primitiva è sempre una funzione continua. Fatto importante:
mentre la derivata, se esiste, è unica, la primitiva, se esiste, non è mai unica. Infatti,
se c ∈ ℝ, per
ogni x0 ∈ (a,b)
vale:
Dx0 F(x) + c = F′(x
0).
Dunque, F(x)
ed F(x) + c
sono primitive della medesima funzione. Vale anche il viceversa:
Teorema 126 Siano F1(x)
ed F2(x)
due primitive della funzione f(x)
sul medesimo intervallo (a,b).
Esse “differiscono per una costante”, ossia esiste c ∈ ℝ
tale che
F1(x) = F2(x) + c.
Dim. Si veda il Lemma 123. ■
Di conseguenza:
Corollario 127 Supponiamo che f(x)
ammetta primitive su (a,b).
Esiste un’unica primitiva F(x)
che si annulla in un fissato x0 ∈ (a,b).
Dim. Sia infatti F1(x) una
qualsiasi primitiva di f(x)
su (a,b). La primitiva
che si annulla in x0
è
F(x) = F1(x) − F1(x0). ■
L’insieme di tutte le primitive della funzione
f(x) su un
intervallo (a,b)
si indica col simbolo
∫
f(x)dx
e si chiama l’integrale indefinito di f(x).
Si noti che:
Noi useremo il simbolo
∫
x0xf(x)dx
per intendere quella particolare primitiva che si annulla in
x0.
VARIABILE MUTA DI INTEGRAZIONE
Il simbolo
∫
f(x)dx
indica un insieme di funzioni definite su un (sottinteso) intervallo
(a,b).
La lettera che si usa per indicare la variabile indipendente non ha
alcuna influenza sul concetto di primitiva. Per questo potremmo
cambiarla arbitrariamente scrivendo per esempio
F(x) + c = ∫
f(x)dx = ∫
f(s)ds = ∫
f(ξ)dξ
ecc. Analogamente, per indicare la primitiva che si annulla in
x0
potremo scrivere
∫
x0xf(x)dx = ∫
x0xf(s)ds = ∫
x0xf(ξ)dξ.
Per questa ragione la lettera che indica la “variabile” sotto il segno di
primitiva si chiama variabile muta d’integrazione
Attenzione che il simbolo
∫
dx
e il termine “integrale”
hanno vari significati concettualmente diversi. Il significato
di “primitiva” è solo uno di essi.
Sebbene questo non sia esplicitamente richiesto dalla
definizione di primitiva, nella maggior parte dei casi le primitive di
f(x) su
(a,b) sono definite e continue
sull’intervallo [a,b].
In tal caso,
∫
axf(x)dx
indicherà quella particolare primitiva che si annulla in
a. Se
F(x) è una qualsiasi
primitiva (continua in a)
di f(x),
sarà
∫
axf(x)dx = F(x) − F(a)
Infine, notiamo questo teorema, che proveremo in seguito (si veda il Teorema 195):
Teorema 128 Ogni funzione continua su un intervallo ammette ivi
primitive.
Si noti però che esistono funzioni continue la cui primitiva non si può esprimere in
modo elementare. Per esempio, non è possibile rappresentare le primitive di
ex2 oppure
di sin x2
mediante funzioni “elementari”. Se una funzione definita su
(a,b) non
è continua, essa può ammettere primitive o meno. E’ importante conoscere il
risultato:
Teorema 129 Se
f(x)
è definita su
(a,b)
ed ha un salto in
x0 ∈ (a,b)
allora essa non ammette primitive.
Per esempio, la funzione f(x) = sgn(x)
non ammette primitive in nessun intorno di
0.
Regole di calcolo per le primitive
NOTAZIONE
In questo paragrafo, useremo lettere maiuscole
e le corrispondenti lettere minuscole,
F
ed f,
per indicare funzioni. Intenderemo che tra queste coppie di funzioni
valga
f(x) = F′(x).
Le primitive si calcolano leggendo alla rovescia la tabella delle derivate e usando le
regole di calcolo che ora vediamo e che sono conseguenza della linearità della
derivata, della regola di Leibniz e della regola di derivazione della funzione
composta. Nel calcolo delle primitive, è utile ricordare anche le due formule
seguenti, viste all’esempio 98:
|
| | | |
| D log tan x
2 = 1
sin x | D log tan x
2 + π
4 = 1
cos x |
| | |
|
| | |
Esaminiamo ora come si usano le tre regole di derivazione per il calcolo delle
primitive.
Conseguenza della linearità della derivata è la linearità dell’integrale
ossia
c∫
f(x)dx + d∫
g(x)dx = ∫
cf(x) + dg(x) dx
(c e
d sono
numeri).
Conseguenza della regola di Leibniz è una regola che si chiama integrazione per parti
Siano F(x) e
G(x) primitive
rispettivamente di f(x)
e g(x) su
(a,b).
Allora vale
∫
f(x)G(x)dx = F(x)G(x) −∫
F(x)g(x)dx
Questa regola si ricorda facilemte intendendo che
“d” indichi la
derivata, cosìche dx
indica 1.
Con questa convenzione, la regola di integrazione per parti si scrive
∫
F(x)dG(x) = F(x)G(x) −∫
G(x)dF(x).
La regola di integrazione per parti è utile quando è dato da calcolare l’integrale
di sinistra, che non si sa calcolare direttamente, mentre invece si riesce a calcolare
quello di destra.
Esempio 130 Si vogliono le primitive di xex.
Una primitiva del fattore ex
è nota (ed è ex
stessa). Quindi si può procedere cosí:
∫
xexdx = ∫
xdex = xex −∫
exdx = xex − ex + c.
L’uso “sbagliato” della regola di integrazione per parti conduce in genere ad un
integrale più complicato di quello di partenza, ma questo non sempre è un male.
Esempio 131 La tabella delle derivate non aiuta a calcolare le primitive di
1
(1 + x2)2.
Si conosce però una primitiva di 1∕(1 + x2):
arctan x + c = ∫
1
1 + x2dx.
Usiamo la formula di integrazione per parti trovando: |
∫
1
1 + x2dx = x 1
1 + x2 −∫
xd 1
1 + x2 = x 1
1 + x2 + ∫
x 2x
(1 + x2)2dx
= x 1
1 + x2 + 2 ∫
x2 + 1 − 1
(1 + x2)2 dx = x 1
1 + x2 + 2 ∫
1
1 + x2dx − 2 ∫
1
(1 + x2)2dx.
|
Si trova quindi
2 ∫
1
(1 + x2)2dx = x
1 + x2 + arctan x + c.
Conseguenza della regola di derivazione della funzione
composta è la regola di integrazione per sostituzione Sia
F(y) una
primitiva di f(y)
su (a,b) e sia
G(x) definita
su (α,β).
Allora vale
∫
f(G(x))G′(x)dx = F(G(x)) + c.
Anche questa regola si ricorda meglio se si integrpreta
“d”
come segno di derivata perché cosìessa prende la forma
∫
f(G(x))dG(x) = F(G(x)) + c
e si può interpretare come segue: alla
G(x) si sostituisce
la “variabile” u
e si calcola
∫
f(u)du = F(u) + c.
Quindi ad u si
sostituisce nuovamente G(x).
La semplice formulazione non inganni. Questa è la più diffcile delle regole da
usare e presenta due casi distinti.
-
- Caso 1) L’integrando ha forma f(G(x))g(x)
con g(x) = G′(x).
In questo caso, si calcola F(y)
e al posto di y
si sostituisce G(x).
Esempio 132 Si voglia calcolare
∫
(sin x)2 cos xdx.
Si scriva quest’integrale come
∫
sin x2d sin x.
Si sostituisca
sin x = u
e si noti che
∫
u2du = 1
3u3 + c.
Si sostituisca ora u
con sin x.
Si ottiene
∫
(sin x)2 cos xdx = 1
3 sin 3x + c. ■
-
- Caso 2) La sostituzione “va inventata”.
In questo caso è data da calcolare la primitiva di una funzione
f(x)
e l’abitudine o la fantasia porta ad immaginare una funzione
G(x) tale che sia facile il
calcolo delle primitive di f(G(x))G′(x).
Le formule di trigonometria, circolare o iperbolica, spesso suggeriscono la
sostituzione.
Esempio 133 Si vogliono le primitive della funzione
f(x) = 1 − x2.
Ovviamente x ∈ (−1, 1).
Non è affatto evidente come si possano calcolare queste primitive. Però si
nota che
y = 1 − x2
è la metà superiore della circonferenza trigonometrica e, come si è
notato al paragrafo 2.4, ciascun punto della circonferenza trigonometrica si
rappresenta come (cos 𝜃, sin 𝜃).
La rappresentazione è unica se si sceglie 𝜃 ∈ [0, 2π)
e si ha la semicirconferenza superiore se si sceglie 𝜃 ∈ (0,π).
Ciò suggerisce la trasformazione
x = G(𝜃) = cos 𝜃⇒g(𝜃) = G′(𝜃) = − sin 𝜃.
Sostituendo
x→ cos 𝜃 d x→ d cos 𝜃 = − sin 𝜃d 𝜃
si trova l’integrale
−∫
sin 2𝜃d𝜃.
Ricordando la formula di bisezione,
sin 2𝜃 = 1
2 1 − cos 2𝜃.
Quindi
−∫
sin 2𝜃d𝜃 = −1
2𝜃 + 1
4 sin 2𝜃 + c,𝜃 ∈ (0,π).
Il calcolo però non è concluso. Questa è la primitiva
F(G(𝜃)) di
f(G(𝜃))G′(𝜃) mentre noi
vogliamo F(x). La
funzione cos 𝜃 su
[0,π] è invertibile: la sua
funzione inversa è arccos x.
Al posto di 𝜃 si
sostituisce ora arccos x
e si trova |
F(x) = −1
2 arccos x + 1
4 sin 2 arccos x
= −1
2 arccos x + 1
2 sin arccos x cos arccos x
= −1
2 arccos x + x1 − cos arccos x 2
= −1
2 arccos x + x1 − x2. ■
|
Usando la formula
cosh 2x − sinh 2x = 1
si calcolino le primitive di
f(x) = 1 + x2.
Primitive di funzioni razionali
Dalla tabella delle derivate si vede che
∫
xndx = 1
n + 1xn+1 + c.
Combinando quest’osservazione con la linearità dell’integrale, segue che ogni
polinomio ammette primitive, e queste sono polinomi. La tabella delle
derivate mostra che |
∫
1
x − adx = log |x − a| + c,∫
1
1 + x2dx = arctan x + c,∫
1
x2dx = −1
x + c.
|
Dunque, integrando funzioni razionali si possono trovare funzioni “più
complicate”; si possono trovare logaritmi ed arcotangenti. Proviamo ora che
funzioni razionali, logaritmo ed arcotangente bastano ad integrare tutte le funzioni
razionali.
Osservazione sulla notazione
Le primitive devono essere definite su intervalli. Dunque,
log |x − a| ed
1∕x
non sono funzioni primitive. Sono funzioni primitive le funzioni
|
log(x − a)x > a, log(a − x)x < a,
1
xx > 0, 1
xx < 0.
|
Per non appesantire la notazione, in genere si lascia al lettore di
determinare l’intervallo su cui lavorare. Quest’osservazione, che sembra qui
un po’ capziosa, assumerà un significato fisico importante quando
studieremo le equazioni differenziali.
Ricordiamo che come funzione razionale si intende il quoziente di due
polinomi,
R(x) = p(x)
d(x).
Se il grado di p(x)
è maggiore o uguale di quello del denominatore, si può dividere ottenendo
R(x) = p(x)
d(x) = p0(x) + q(x)
d(x)
e il grado di q(x) è
minore di quello di d(x).
Dato che le primitive dei polinomi si sanno calcolare, basta calcolare le primitive
di
q(x)
d(x),grado di q < grado di d.
Il calcolo delle primitive ora si fa identificando i poli della funzione razionale; ossia i
punti in cui si annulla il denominatore, che possono essere reali o complessi. I
numeri complessi si studieranno in seguito, ma per i calcoli che ora andiamo a fare
non ne abbiamo realmente bisogno. Il calcolo delle primitive si fa con i metodi
illustrati negli esempi seguenti.
Poli reali semplici E’ il caso in cui
d(x) ha grado
n ed inoltre
ha n
radici distinte. Se ciò vale si dice che la funzione
f(x) ha
n
poli semplici In questo caso si procede come nell’esempio che segue:
r(x) = x2 − 4x + 1
x(x − 2)(x + 3).
Si scrive r(x)
come somma:
r(x) = A
x + B
x − 2 + C
x + 3
Riducendo allo stesso denominatore si trova che i tre numeri
A,
B,
C
devono verificare
|
A(x − 2)(x + 3) + Bx(x + 3) + Cx(x − 2)
= x2(A + B + C) + x(A + 3B − 2C) + (−6A)
= x2 − 4x + 1.
| (4.12) |
Quindi, i valori di A,
B,
C si
trovano risolvendo il sistema
− 6A =1
A + 3B − 2C = − 4
A + B + C =1 da cui A = −1
6
B = − 3
10
C =22
15.
Noti i valori delle costanti A,
B e
C, il
calcolo della primitiva è immediato. Questo metodo può usarsi tutte le volte che
il denominatore ha tutte le radici reali e distinte.
Risolvere questo sistema è alquanto fastidioso. Un metodo più
semplice è il seguente: sostituendo
x = 0
nei due membri di (4.12) si trova immediatamente
−6A = 1e quindi A = −1∕6.
Analogamente sostituendi x = 2
si trova B = −3∕10
e sostituendo x = −3
si trova il valore di C.
Poli reali semplici o meno Se un polinomio
P(x) si
fattorizza come
P(x) = (x − x0)rQ(x),Q(x
0)≠0,
si dice che x0 è uno
zero di molteplicità r
di P(x); e
se P(x) è
il denominatore di una funzione razionale il cui numeratore non si annulla in
x0, si dice
che x0 è un
polo di molteplicità r
della funzione razionale. In questo caso si procede come nell’esempio seguente:
Esempio 134
r(x) = x2 − 4x + 1
(x − 2)2(x + 3).
Il polo semplice
3
si tratta come sopra: gli si fa corrispondere un’addendo
C
x + 3.
Invece al polo doppio
2
si fa corrispondere l’addendo
Ax + B
(x − 2)2
Imponendo
x2 − 4x + 1
(x − 2)2(x + 3) = Ax + B
(x − 2)2 + C
x + 3
Riducendo allo stesso denominatore si trova che i numeri
A,
B e
C
devono verificare l’identità |
x2 − 4x + 1 = (Ax + B)(x + 3) + C(x − 2)2
| (4.13) |
e quindi
(A + C)x2 + (3A + B − 4C)x + 3B + 4C = x2 − 4x + 1.
Usando il principio di identità dei polinomi si trova il sistema
A + C = 1,3A + B − 4C = −4,3B + 4C = 1
da cui
A = 3
25,B = −21
25,C = 22
25.
A questo punto si nota che
Ax + B
(x − 2)2 = A(x − 2) + (2A + B)
(x − 2)2 = A
x − 2 + 2A + B
(x − 2)2.
La primitiva di questi addendi si trova direttamente dalla tavola delle derivate.
Anche in questo caso, può essere più semplice fare opportune
sostituzioni per ricavare immediatamente almeno una parte dei
coefficienti. Per esempio sostituendo
x = −3
in (4.13) si ottiene immediatamente
C = 22∕25
e quindi
(Ax + B)(x + 3) = x2 − 4x + 1 −22
25(x − 2)2.
Sostituendo x = 0
si ottiene subito, B = −21∕25.
Tenendo conto di ciò e sostituendo
x = 2
si trova A = 3∕25.
In generale, ad ogni polo x0
di molteplicità n
si fa corrispondere un addendo |
p(x)
(x − x0)n.Il grado di p(x) è n − 1.
| (4.14) |
Le primitive di questi addendi possono calcolarsi perché ciascuno di essi a sua
volta può decomporsi come segue: |
p(x)
(x − x0)n = A1
x − x0 + A2
(x − x0)2 + ⋯ + An
(x − x0)n.
| (4.15) |
Talvolta però, specialmente quando
n = 2 oppure
n = 3,
opportuni artifici, come quelli visti all’Esempio 134, conducono al calcolo delle
primitive di (4.14) senza passare attraverso l’ulteriore decomposizione (4.15).
Osservazione 135 Notiamo che |
p(x)
(x − x0)n = A1
x − x0 + A2
(x − x0)2 + ⋯ + An
(x − x0)n
= A1
x − x0 + d
dx − A2
x − x0 + ⋯ + An
(1 − n) 1
(x − x0)n−1 .
|
Dunque, il secondo membro di (4.15) si può anche scrivere come
A1
x − x0 + + d
dx r(x)
(x − x0)n−1.Il grado di r(x) è n − 2.
Quindi se per esempio ci sono due poli reali
x0 ed
x1 di
molteplicità n1
ed n2 (maggiore
di 1) a
tali poli si possono associare gli addendi
1
x − x0+ 1
x − x1+ d
dx r(x)
(x − x0)n0−1(x − x1)n1−1.Il grado di r(x) è n0 + n1 − 3
ossia r(x)
ha grado minore di una unità del grado del denominatore. I coefficienti di
r(x) si
determinano facendo la derivata del quoziente, riducendo i due membri al medesimo
denominatore e imponendo l’uguaglianza dei polinomi a numeratore. Una volta
determinato r(x),
la primitive cercate sono
log |x − x0| + log |x − x1| + r(x)
(x − x0)n0−1(x − x1)n1−1 + c. ■
Il caso generale In generale, il denominatore avà anche zeri
non reali. Noi ci limitiamo al caso in cui gli zeri non reali sono
semplici.
Il prototipo è il caso
1
x2 + bx + c,c −1
4b2 = γ2 > 0.
In questo caso, si può “completare il quadrato”, scrivendo
1
x + b
2 2 + γ2 = 1
γ2 1
1 + x
γ + b
2γ 2
le cui primitive sono
1
γ arctan x
γ + b
2γ + c.
E ora, nel caso in cui ci siano anche poli reali, semplici o meno, si decompone la
funzione razionale in una somma di termini del tipo
p(x)
(x − x0)n
se x0
è radice reale del denominatore, di molteplicità
n. Il polinomio
p(x) deve avere
grado n − 1.
Le primitive di questi addendi si calcolano come abbiamo già visto. A ciascuno dei
fattori x2 + bx + c
del denominatore, con discriminante negativo, si fa corrispondere un addendo della
forma
Ax + B
x2 + bx + c.
La decomposizione appena descritta delle funzioni razionali si chiama
decomposizione in fratti semplici
Osservazione 136 Il metodo descritto all’Osservazione 135 si può anche
usare quando il denominatore ha fattori (x2 + bx + c)k,
privi di zeri. In tal caso si isolano gli addendi Ax+B
x2+bx+c
e al denominatore del termine di cui si calcola la derivata si aggiunge un fattore
(x2 + bx + c)k−1.
Il grado del polinomio al numeratore (che è da determinare) va aumentato di
k − 2. ■
4.6.1 Primitive generalizzate
Supponiamo che F(x)
sia continua su (a,b)
e che valga
F′(x) = f(x)
in tutti i punti di (a,b),
salvo un numero finito di essi. In tal caso si dice che
F(x) è una
primitiva generalizzata di f(x).
Si noti che F(x)
potrebbe non essere derivabile in alcuni punti di
(a,b) (in
numero finito) e quindi la continuità va imposta esplicitamente. Le primitive
generalizzate si calcolano facilmente procedendo come nell’esempio seguente.
Esempio 137 Sia
f(x) = x2 sex < 0
cos x sex > 0.
Le funzioni
F1(x) = (1∕3)x3 + c,F
2(x) = sin x + d
verificano rispettivamente
F1′(x) = f(x) sex < 0
F2′(x) = f(x) sex > 0.
La funzione F(x) = F1(x)
per x < 0
ed F2(x) = F2(x)
per x > 0
NON è una primitiva di f(x)
perché non è definita in 0;
e non lo è in generale nemmeno se si assegna ad essa un valore in
0
perché in generale non sarà continua. Però vale
lim x→0−F1(x) = c
lim x→0+F2(x) = d.
Si imponga allora prima di tutto l’uguaglianza dei limiti ossia in
quest’esempio si imponga
c = d.
Quindi si estenda
F(x)
per continuità anche nel punto
0
ossia, in quest’esempio si imponga
F(0) = c = d.
Si è trovata cosìuna primitiva generalizzata di f(x).
Dunque, l’insieme di tutte le primitive generalizzate di f(x)
è
1
3x3 + c sex ≤ 0
c + sin x sex > 0.
Si noti che la f(x)
non era definita in x = 0,
mentre F(x)
deve essere definita su un intervallo, e quindi anche in 0.
Se si fosse assegnato
f(0) = 7,
o qualsiasi altro numero, niente sarebbe cambiato nella procedura descritta.
Infatti, non si richiede né che F(x)
sia derivabile in 0
né, se derivabile, si richiede F′(0) = f(0).
Dunque, le funzioni
F(x) = 1
3x3 + c sex ≤ 0
c + sin x sex > 0
sono anche le primitive di
f(x) = x2 sex < 0
f(x) = 7 sex = 0
cos x sex > 0. ■
L’esempio precedente si adatta in generale e in particolare si potrebbe provare che
l’insieme delle primitive generalizzate, se non è vuoto, dipende da una
(sola) costante arbitraria.
4.7 Alcuni esercizi
- (⋆)
Il teorema dei valori intermedi asserisce che una funzione continua
trasforma intervalli in intervalli. Si mostri che esistono funzioni non
continue che hanno questa proprietà esaminando le funzioni
f(x) = sin 1
x sex≠0 a se x = 0.
Si consideri separatamente il caso |a|≤ 1
ed il caso |a| > 1
e si noti che, in uno dei due casi, questa funzione, discontinua in
0,
trasforma intervalli in intervalli.
- Il teorema dei valori intermedi combinato col teorema di Weierstrass
implica che una funzione continua definita su un intervallo chiuso lo
trasforma in un intervallo chiuso. L’asserto analogo non vale per gli
intervalli aperti: si costruisca un esempio di funzione continua su un
intervallo aperto, la cui immagine è un intervallo chiuso.
- (⋆)
Le funzioni monotone che trasformano intervalli in intervalli sono
ovunque continue. Si spieghi la ragione e si mostri un esempio di funzione
monotona definita su ℝ,
con un unico punto di discontinuità e la cui immagine non contiene
l’insieme (−1, 0) ∪ (0, 1)
ma contiene il punto 0.
- Sia f(x)
monotona su [a,b].
Mostrare che la funzione ha sia punti di massimo che di minimo assoluto.
- (⋆)
Sia f(x)
crescente su [a,b]
e sia x0 ∈ (a,b)
un suo punto di discontinuità. Si vuol sapere se è possibile che
ambedue gli insiemi f([a,x0])
ed f([x0,b])
siano intervalli chiusi.
- Sia f(x)
crescente su [a,b]
e sia x0 ∈ (a,b)
un suo punto di discontinuità. Si vuol sapere se è possibile che l’insieme
f([a,x0])
sia un intervallo aperto.
- (⋆)
Sia f(x)
monotona su [a,b]
e sia x0 ∈ (a,b).
Supponiamo che esista lim x→x0f(x).
Mostrare che f(x)
è continua in x0.
Vale quest’asserto se x0 = a
oppure x0 = b?
- per x ∈ [0, 1]
sia f(x) = sgn(M(x)) ex
(si ricordi che M(x)
indica la mantissa di x).
Tracciare il grafico di f(x),
studiarne la monotonia e la continuità su [0, 1].
- Sia f(x) ∈ C1(ℝ)
e sia g(x) = 3x.
Provare che se i grafici delle due funzioni si intersecano in due punti allora
la tangente al grafico di f(x)
ha pendenza 3
in almeno un punto. Provare inoltre che esiste un intervallo I
su cui f(x)
è crescente.
- (⋆)
Usando il teorema di Rolle, si provi che se una funzione è di classe
C2
su (a,b)
e se f″(x)
non si annulla allora ogni coppia di tangenti al grafico di f(x)
si interseca.
- (⋆)
Su x > 0
vale 0 < sin x < x.
Usare questa proprietà, il teorema di Rolle ed il teorema dei valori
intermedi per provare che cos x > 1 − x2∕2
sia per x > 0
che per x < 0.
- Si è visto che
d
dx sett thx = 1
1 − x2, d
dx sett cthx = 1
1 − x2.
Spiegare se è vero o meno che le due funzioni sett thx
e sett cthx
differiscono per una costante.
- Le due funzioni f(x) = arcsin x
e g(x) = − arccos x
sono definite sul medesimo intervallo [−1, 1]
e su (−1, 1)
hanno la stessa derivata. Dunque differiscono per una costante. Trovare
il valore della costante e illustrare questo fatto geometricamente a partire
dai grafici delle funzioni sin x
e cos x
(si confronti con l’esercizio 39 del Capitolo 1).
- Sia
f(x) = arctan x,g(x) = arctan x − 1
x + 1.
Mostrare che f′(x) = g′(x).
Tracciare il grafico delle funzioni e notare che le due funzioni non
differiscono per una costante. Spiegare.
- Sia
f(x) = arctan x,g(x) = arctan x + 1
x − 1.
Notare che
d
dx f(x) + g(x) = 0.
E’ vero che f(x) + g(x)
è costante?
- Si mostri, sia mediante le formule di trigonometria che mediante il calcolo
delle derivate:
cotan1
2x = cotanx + 1
sin x.
- Mostrare che
arctan x + arctan 1
x
è costante per x > 0
e per x < 0
e calcolarne i valori.
- (⋆)
Si ricordi che
tan(α − β) = tan α − tan β
1 + (tan α)(tan β).
Dire se si può applicare questa formula con
α = arctan x,β = arctan 1
x
per calcolare il valore di arctan x + arctan(1∕x).
Usare il risultato trovato all’esercizio 17.
- Rolle (1652-1719) enuncia il suo teorema nel suo libro Traité d’algebre
del 1690, limitandosi a considerare “funzioni algebriche”, ossia funzioni
espresse mediante polinomi. Con linguaggio moderno, l’enunciato di
Rolle è il seguente: tra due zeri reali consecutivi della derivata di una
funzione algebrica si trova al più uno zero della funzione stessa. Si
provi che questo enunciato è vero usando la formulazione moderna del
Teorema di Rolle, ossia l’enunciato del Teorema 118.
- Si calcolino le primitive
∫
1
m2 − x2dx
e si mostri che l’uguaglianza
∫
1
m2 − x2dx = arcsin x
m + c
non è corretta. Si trovi l’espressione giusta. In modo analogo si tratti
∫
m2 + x2dx.
- Siano f(x)
e g(x)
due funzioni dotate di primitive F(x)
e G(x)
su un intervallo (a,b).
Sia F(x0) = G(x0)
e sia f(x) ≥ g(x)
per x > x0.
Si deduca che vale la proprietà di monotonia del calcolo delle primitive
F(x) ≥ G(x)
per x ≥ x0.
- Sia f(x) ∈ C1(a,b)
e sia |f′(x)| < K
su [a,b].
Usando il Teorema di Lagrange, si mostri che per ogni coppia di punti
x1
ed x2
in [a,b]
vale
f(x1) − f(x2) ≤ K|x1 − x2|.
- (⋆)
Sia F(x)
primitiva su [a,b]
della funzione f(x)
continua su [a,b]
e valga f(x) ≤ K.
Siano x(t)
ed y(t)
funzioni continue su un intervallo [α,β],
a valori in [a,b].
Mostrare che
∫
αt f(x(t)) − f(y(t)) dt ≤K max
s∈[α,t] x(s) − y(s) (t − a).
Capitolo 5
Teoremi di l’Hospital e di Taylor
Ormai so che l’acqua scorre sempre verso il basso, se non
quando è buio. So che questo accade perché lo stagno non
si prosciuga mai, come naturalmente succederebbe se l’acqua
non ritornasse in su. Diario di Eva, Il diario di Adamo ed Eva
di Mark Twain
In questo capitolo si presentano i Teoremi di l’Hospital e la formula di Taylor e le loro
conseguenze, concludendo lo studio sia locale che globale delle funzioni. Il Teorema
di L’Hospital serve per il calcolo dei limiti quando si incontrano forme
indeterminate di tipo fratto mentre la formula di Taylor estende la prima
e la seconda formula degli incrementi finiti al caso in cui una funzione
f(x)
ammette più derivate.
5.1 Teorema di l’Hospital
E’ un teorema che è utile per il calcolo di limiti nel caso che si incontri una forma
indeterminata di tipo fratto,
0
0 oppure∞
∞,
nel calcolo di un limite per x → α
dove α può essere
un numero oppure +∞
oppure −∞.
Anzi, se α ∈ ℝ
il Teorema di l’Hospital si può usare anche per il calcolo dei limiti direzionali
x → α+ oppure
x → α−. Illustriamolo nel
caso del limite per x → α−
intendendo che se α = +∞ questo
sarà il limite per x → +∞.
Ricordiamo lo scopo: calcolare
lim x→α−f(x)
g(x)
quando si incontra la forma indeterminata
0∕0 oppure
∞∕∞. Le
ipotesi sono le seguenti:
Il teorema asserisce:
Teorema 138 (di l’Hospital) Se valgono le ipotesi enunciate sopra, esiste
lim x→α−f(x)
g(x)
e inoltre, con
β
dato da (5.1),
lim x→α−f(x)
g(x) = β.
La dimostrazione, alquanto complessa, viene omessa.
Esempio 139 Illustriamo alcuni esempi ed alcuni problemi che possono
incontrarsi nell’uso di questo teorema.
- Consideriamo il limite
lim x→+∞ log x
x .
Le funzioni a numeratore e denominatore verificano le ipotesi del
Teorema di l’Hospital e inoltre (D
indica l’operazione di derivazione)
lim x→+∞D(log x)
D(x) = lim x→+∞1
x = 0.
Quindi si ha anche
lim x→+∞ log x
x = 0.
In modo analogo si provi che
lim x→+∞ex
x = +∞.
- Consideriamo ora
lim x→+∞ex
x2.
Proviamo a fare il quoziente delle derivate. Si trova
ex
2x.
Dato che, grazie ad un preventivo uso del teorema di l’Hospital, questo
limite si conosce, ed è +∞,
e le altre ipotesi del teorema valgono, si può concludere che
lim x→+∞ex
x2 = +∞.
Ossia, il teorema di l’Hospital si può applicare più volte in sequenza.
- Non è detto che il Teorema di L’Hospital permetta sempre di calcolare
il limite, nemmeno se le ipotesi sono soddisfatte. Per esempio, sia
f(x) = sinh x
e g(x) = cosh x.
E’ immediato dalla definizione delle funzioni iperboliche che
lim x→+∞ sinh x
cosh x = 1.
Tutte le ipotesi del teorema di l’Hospital valgono per questo quoziente,
ma il teorema stesso non serve al calcolo del limite perché derivando
numeratore e denominatore si trova alternativamente
cosh x
sinh x, sinh x
cosh x, cosh x
sinh x…
Ossia, usando quante volte si voglia il teorema di l’Hospital si finisce
sempre sulla medesima forma indeterminata. Un esempio simile è il
calcolo del limite
lim x→+∞1
x log xlog x.
Il quoziente delle derivate è
1
x log xlog x + log log x
x log xlog x
e quindi fa intervenire nuovamente proprio il quoziente di cui si intendeva
calcolare il limite. Si noti che questo limite è stato calcolato per
sostituzione all’Esempio 84.
- Può anche essere che il limite del quoziente delle funzioni esista, ma
che non esista quello del quoziente delle derivate. Notando che
sin 1
x < 1
si vede che
lim x→0x2 sin 1∕x
sin x = 0.
Se si calcola il quoziente delle derivate si trova
2x sin 1∕x − cos 1∕x
cos x ,
privo di limite per x → 0,
nonostante che le altre condizioni del teorema di l’Hospital siano
soddisfatte.
- Se si usa il teorema di L’Hospital quando le ipotesi non sono soddisfatte,
si possono trovare risultati sbagliati. Per esempio,
lim x→0+ 1
x = +∞.
Le ipotesi del teorema di L’Hospital non sono soddisfatte da questo
quoziente, che non conduce ad una forma indeterminata. Facendo il
limite del quoziente delle derivate si trova
lim x→0+0
1 = 0≠ + ∞.
- Il teorema di L’Hospital talvolta può applicarsi e conduce al risultato
corretto, ma il calcolo fatto è fallace perché tautologico; ossia perché
usa proprio l’informazione che si sta cercando. Per esempio, usando il
teorema di L’Hospital,
lim x→0 sin x
x = lim x→0 cos x
1 = 1.
Sembra quindi di aver trovato un modo molto veloce per il calcolo del
limite notevole. Ciò è però falso perché in questo calcolo si è usato
D sin x = cos x,
formula che si dimostra proprio a partire dal limite notevole di
(sin x)∕x.
- Infine, notiamo che col teorema di l’Hospital si possono anche calcolare
certi limiti che apparentemente non sono nella forma di quoziente. Per
esempio, si voglia studiare
lim x→0x log x.
Scrivendo questo limite come
lim x→0 log x
1∕x
si ha una forma indeterminata (−∞)∕(+∞)
a cui il Teorema di l’Hospital può applicarsi. Il quoziente delle derivate
è
lim x→0 1
x 1
(−1∕x2) = lim x→0(−x) = 0
e quindi
lim x→0 log x
1∕x = 0.
Di consequenza si deduce anche
lim x→0xx = lim
x→0elog xx
= lim x→0ex log x = 1. ■
Infine, osserviamo la seguente conseguenza del Teorema di l’Hospital. Sia
F(x) una
primitiva di f(x)
sull’intervallo [a,b]
e supponiamo che
f(x) = o(x − a).
Usiamo il Teorema di l’Hospital per calcolare |
lim x→aF(x) − F(a)
(x − a)2 = lim x→a F′(x)
2(x − a)
= lim x→a f(x)
2(x − a) = lim x→a o(x − a)
2(x − a) = 0.
|
Ciò mostra che
F(x) − F(a) = o(x − a)2.
Più in generale,
Teorema 140 Sia
F(x)
primitiva di
f(x)
sull’intervallo
(a,b)
e supponiamo che
f(x) = o(x − a)n.
Allora,
F(x) − F(a) = o(x − a)n+1.
5.1.1 Calcolo di derivate direzionali
Un argomento analogo a quello usato nella dimostrazione del Teorema 140 dà
anche un modo molto utile che può usarsi per il calcolo di derivate direzionali. Il
problema è questo: talvolta si può provare che una funzione è derivabile su
(a,x0) e su
(x0,b)
e usando le regole di derivazione se ne calcola facilmente la derivata.
E’ invece diffcile vedere se esistono le derivate direzionali in
x0. Una condizione suffciente
per l’esistenza di f′(x
0)
è la seguente:
Teorema 141 Sia f(x)
continua in x0
e inoltre derivabile in (x0,b).
Se esiste il limite direzionale f′(x
0+),
ossia se siste
lim x→x0+f′(x),
allora esiste anche la derivata direzionale
f+′(x
0)
e inoltre si ha l’uguaglianza
f+′(x
0) = lim x→x0+f′(x) = f′(x
0+).
Dim. Per definizione,
f+′(x
0) = lim x→x0+f(x) − f(x0)
x − x0 .
Il limite è una forma indeterminata
0∕0, perché la funzione
è continua in x0.
Per il calcolo di questo limite si può usare il teorema di l’Hospital,
lim x→x0+f(x) − f(x0)
x − x0 = lim x→x0+f′(x)
1 = lim x→x0+f′(x),
ovviamente se l’ultimo limite scritto
esiste. ■
Asserto analogo vale per la derivata sinistra:
Teorema 142 Sia f(x)
continua in x0
e inoltre derivabile in (a,x0).
Se esiste
lim x→x0−f′(x)
allora esiste
f−′(x
0)
e inoltre
f−′(x
0) = lim x→x0−f′(x) = f′(x
0−).
E quindi:
Teorema 143 Se f(x)
è
- derivabile in (a,x0)
- derivabile in (x0,b)
- continua in x0
- esiste lim x→x0f′(x)
allora la funzione f(x)
è derivabile in x0
e vale
f′(x
0) = lim x→x0f′(x).
Osservazione 144 L’ipotesi che f(x)
sia continua in x0
è essenziale nel Teorema 143. Se non vale, le tangenti nei punti (x,f(x))
tendono a diventare parallele quando x → x0,
senza sovrapporsi per x = x0,
si veda la figura 5.1. ■
Segue dal Teorema 143:
Corollario 145 Se
f′(x)
è definita su
(a,b)
e discontinua in
x0 ∈ (a,b)
allora la discontinuità è di seconda specie.
Dim. Ricordiamo che f′(x)
ha discontinuità eliminabile oppure di prima specie in
x0 ∈ (a,b) quando esistono ambedue
i limiti direzionali lim x→x0−f′(x)
e lim x→x0+f′(x), ed uno almeno
è diverso da f′(x
0).
Per ipotesi, f′(x
0)
esiste e quindi f(x)
è continua in x0.
Il teorema precedente garantisce che i due limiti direzionali, se esistono, valgono
f′(x
0); ossia
x0
non può essere né punto di salto né discontinuità eliminabile di
f′(x). ■
Questo risultato permette in particolare di asserire che la funzione
sgn(x)
non è una funzione derivata in nessun intorno di
0, e
quindi non ammette primitive. Esistono però funzioni ovunque derivabili, la
cui derivata ammette discontinuità di seconda specie. Un esempio è la funzione
f(x) = x2 sin(1∕x) per
x≠0, ed
f(0) = 0.
5.2 La formula di Taylor
La formula di Taylor è un’estensione della prima o della seconda formula degli
incrementi finiti. Vediamo separatamente i due casi.
5.2.1 La formula di Taylor con resto in forma di Peano
La formula di Taylor (con resto in forma di Peano) è un’estensione
della prima formula degli incrementi finiti a funzioni che in un punto
x0
hanno più di una derivata. Notiamo che:
- il punto x0
è indicato in colore, x0,
per sottolineare che è considerato fissato, mentre la variabile si indica
con x;
- se una funzione ha n
derivate in x0
allora ha n − 1
derivate in un intorno di x0.
Supponiamo che in x0
esista la derivata seconda. Allora, si può scrivere la prima formula degli incrementi finiti
in x0 per la
funzione f′(x): |
f′(x) = f′(x
0) + (x −x0)f″(x
0) + o(x −x0).
| (5.2) |
Per definizione, f′(x) ammette
primitive e x → (x −x0)f″(x0) ammette
primitive. Dunque anche o(x −x0)
ammette primitive. Le primitive che si annullano in
x0 di
f′(x), di
f′(x
0) e di
(x −x0)f″(x0) (funzioni
della variabile x)
sono rispettivamente |
f(x) − f(x0),
f′(x
0)(x −x0),
1
2f″(x0)(x −x0)2.
|
Come si è notato, da (5.2) si vede che anche
o(x −x0)
ammette primitive e, per il Teorema 140,
∫
x0x o(s − x
0)ds = o(x −x0)2.
Uguagliando le primitive che si annullano in
x0 dei
due membri di (5.2) si trova
f(x) = f(x0) + f′(x
0)(x −x0) + 1
2f″(x0)(x −x0)2 + o(x −x
0)2.
Quest’argomento si può ripetere se ci sono derivate di ordine successivo. Per esempio, se c’è la
derivata terza in x0,
si può scrivere la prima formula degli incrementi finiti per
f″(x),
f″(x) = f″(x0) + f‴(x0)(x −x0) + o(x −x0).
Prendendo due volte le primitive dei due membri che si annullano in
x0 si
trova
f(x) = f(x0)+f′(x
0)(x−x0)+ 1
2f″(x0)(x−x0)2+ 1
3!f‴(x0)(x−x0)3+ o(x−x
0)3.
In generale, se f(x)
ammette n
derivate in x0,
si trova
f(x) = ∑
k=0nf(k)(x
0)
k! (x −x0)k + o(x −x
0)n.
Questa formula si chiama formula di Taylor con resto in forma di Peano e, più
precisamente:
- il punto x0
si chiama il centro della formula di Taylor;
- il polinomio, della variabile x,
∑
k=0nf(k)(x
0)
k! (x −x0)k
si chiama il polinomio di Taylor di ordine n
di f(x),
di centro x0;
- o(x −x0)n
si chiama il resto in forma di Peano
- E’ particolarmente importante il caso in cui x0 = 0:
f(x) = ∑
k=0nf(k)(0)
k! xk + o(x)n.
Questa formula si chiama formula di MacLaurin Ovviamente, essa è
solamente un caso particolare della formula di Taylor. Per esercizio, si
mostri che le formule degli infinitesimi fondamentali nella tavola 2.7 sono
particolari formule di MacLaurin.
Osservazione 146 Sia f(x)
una funzione dotata di derivata n-mma
in x0
e sia Pn(x)
il suo polinomio di Taylor di grado n
e centro x0.
Esso verifica
f(x) − Pn(x) = o(x − x0)nper x → x
0.
Si potrebbe provare che nessun altro polinomio di grado n
in (x − x0)
ha questa proprietà. ■
5.2.2 La formula di Taylor con resto in forma di Lagrange
La formula di Taylor (con resto in forma di Lagrange) è un’estensione della seconda formula
degli incrementi finiti a funzioni che hanno più di una derivata in un intorno di
x0. Limitiamoci ad
enunciarla. Sia f(x)
definita su (a,b) ed
ivi dotata di n
derivate. Sia x0 ∈ (a,b).
Supponiamo che f(n+1)(x)
esista in (x0,b).
Allora esiste c ∈ (x0,b)
tale che
f(x) = ∑
k=0nf(k)(x
0)
k! (x −x0)k + 1
(n + 1)!f(n+1)(c)(x −x
0)n+1.
Analogo risultato vale, con c ∈ (a,x0)
se f(n+1)(x) esiste
in (a,x0).
L’errore
1
(n + 1)!f(n+1)(c)(x −x
0)n+1
si chiama resto in forma di Lagrange
5.2.3 Polinomio di McLaurin e parità di una funzione
Ricordiamo che una funzione f(x)
dispari e definita in x0 = 0
è ivi nulla. Quest’osservazione è stata usata al paragrafo 3.5 per provare
che le derivate di ordine dispari di una funzione pari sono nulle in
x0 = 0;
le derivate di ordine pari di una funzione dispari sono nulle in
x0 = 0 (si
veda il Teorema 102). Possiamo quindi enunciare:
Teorema 147 Sia p(x) polinomio
di McLaurin di una funzione f(x).
Allora:
- se la funzione è pari, le potenze xn
con n
dispari hanno coeffciente nullo;
- se la funzione è dispari, le potenze xn
con n
pari hanno coeffciente nullo.
Naturalmente, non è vietato che anche i coefficienti di alcune potenze pari siano nulli quando
f(x) è pari (ed analoga
osservazione quando f(x)
è dispari).
5.3 Estremi e convessità
Al Teorema 125 abbiamo visto che i punti di massimo o di minimo di una funzione
continua su un intervallo possono individuarsi studiando la monotonia della
funzione a destra e a sinistra del punto. Qui mostriamo che si possono anche
studiare esaminando le derivate successive nel punto stesso. Inoltre, mostreremo
come studiare la convessità di una funzione.
5.3.1 Derivate successive ed estremi
Sia f(x) derivabile
due volte in x0.
Se f′(x
0)≠0 allora
certamente x0 non
è né punto di massimo né punto di minimo (si ricordi il Teorema di Fermat). Supponiamo
quindi f′(x
0) = 0.
Si ha:
Teorema 148 Se f′(x
0) = 0
e f″(x0) > 0
allora il punto x0
è punto di minimo; Se f′(x
0) = 0
e f″(x0) < 0
il punto x0
è punto di massimo per f(x).
Dim. Scriviamo la formula di Taylor di centro
x0
arrestata al secondo ordine, con resto in forma di Peano. Ricordando che
f′(x
0) = 0 si
vede che
f(x) − f(x0) = 1
2f″(x0)(x − x0)2 + o(x − x
0)2 = (x − x
0)2 1
2f″(x0) + o(1) .
Per x → x0, la
funzione 1
2f″(x
0) + o(1) tende
ad f″(x0)∕2 e quindi in
un intorno di x0
ha il segno di f″(x0)∕2;
il fattore (x − x0)2
è maggiore o uguale a zero e quindi in tale intorno
f″(x0) > 0⇒f(x) − f(x0) > 0; f″(x0) < 0⇒f(x) − f(x0) < 0. ■
Niente può dirsi se f″(x0) = 0.
Però, una dimostrazione in tutto analoga prova che:
Teorema 149 Esista f(2n)(x
0)
e sia f(k)(x
0) = 0
per ogni k < 2n.
Se f(2n)(x
0) > 0
il punto x0
è punto di minimo; se f(2n)(x
0) < 0
il punto x0
è punto di massimo per f(x).
5.3.2 Convessità e punti di flesso
Ricordiamo la definizione di convessità data al paragrafo 1.8.3: una funzione è convessa su un
intervallo [a,b] quando per
ogni coppia di punti x1
ed x2 di
[a,b], la corda
che unisce (x1,f(x1))
ed (x2,f(x2))
sta sopra al grafico della restrizione della funzione ad
(x1,x2).
Ricordiamo anche che una funzione è concava quando
−f(x) è convessa.
La definizione di convessità è stata data usando le secanti, che esistono anche se
f(x) non è derivabile.
Se però f(x) è
derivabile su (a,b)
allora si ha il risultato seguente, illustrato nella figura 5.2 e che non proviamo:
Teorema 150 La funzione
f(x)
è convessa su
(a,b)
se e solo se per ogni
x ∈ (a,b)
e per ogni
ξ ∈ (a,b)
si ha
f(x) ≥ f(ξ) + f′(ξ)(x − ξ).
Ossia, la funzione derivabile
f(x)
è convessa su
[a,b]
se e solo se il suo grafico è ovunque sopra a ciascuna delle tangenti
nei punti del grafico stesso. Si enunci la proprietà analoga per le funzioni
derivabili e concave.
Questa proprietà di tipo geometrico si formula in modo
analitico usando la formula di Taylor. Supponiamo che esista
f″(x) e scriviamo la formula
di Taylor di centro ξ
e resto in forma di Lagrange: |
f(x) −f(ξ) + f′(ξ)(x − ξ) = 1
2f″(c)(x − x0)2
| (5.3) |
Quest’uguaglianza mostra che
se f″(c) ≥ 0 per
ogni c ∈ (a,b)
allora
f(x) ≥ f(ξ) + f′(ξ)(x − ξ).
Dunque:
Teorema 151 Sia f(x)
due volte derivabile su (a,b).
La funzione f(x)
è convessa su (a,b)
se e solo se f″(x) ≥ 0
per ogni x ∈ (a,b).
Sia ora f(x) una funzione
di classe C2. Se
f″(x0) > 0 allora, per il teorema di
permanenza del segno, f″(x) > 0
in un intorno di x0
e in tale intorno la funzione è convessa. Se invece
f″(x0) = 0 ed
f″(x)
cresce oppure decresce, allora la funzione è convessa da una parte di
x0 e
concava dall’altra. Un caso in cui ciò avviene è il seguente:
Teorema 152 Sia f(x)
di classe C3
e sia f″(x0) = 0
ed f‴(x0)≠0.
In questo caso la funzione è convessa da una parte di x0
e concava dall’altra.
Dim. Sia per esempio f‴(x0) > 0.
Allora, per il teorema di permanenza del segno applicato alla funzione
f‴(x), che è continua,
f‴(x) rimane positiva in
un intorno di x0. In tale
intorno, f″(x) è crescente
e quindi negativa per x < x0
(dove la funzione è concava) e positiva per
x > x0
(dove la funzione è convessa. Si tratti in modo analogo il caso
f‴(x0) < 0. ■
Consideriamo più in dettaglio il caso di
f(x) di classe
C3, con
f″(x0) = 0 ma
f‴(x0)≠0. Per fissare
le idee sia f‴(x0) > 0
cosìche f″(x) < 0
per x < x0
ed f″(x) > 0
per x > x0:
la funzione è concava a sinistra e convessa a destra di
x0. Dunque, a
sinistra di x0
il grafico è sotto le tangenti ed a destra è sopra. Vediamo cosa accade in
x0.
Scrivendo la formula di Taylor con resto in forma di Peano si vede che
f(x) −f(x0) + f′(x
0)(x − x0) = (x − x0)3 1
3!f(3)(x
0) + o(1) .
Se f(3)(x
0) > 0,
l’uguaglianza precedente mostra che il grafico della funzione taglia la tangente al
grafico in (x0,f(x0))
e in particolare il grafico è sotto alla tangente per
x < x0 e sopra
per x > x0.
Ciò suggerisce la definizione seguente:
Definizione 153 Sia f(x)
una funzione derivabile su un intervallo (a,b)
che contiene x0.
Se la funzione è convessa su (a,x0)
e concava su (x0,b)
(o viceversa), il punto x0
si dice punto di flesso per f(x).
Si dice che x0
è punto di flesso ascendente per f(x)
se il grafico di f(x)
è sotto la tangente in (x0,f(x0))
per x < x0
e sopra per x > x0;
Il punto x0
si dice punto di flesso discendente se il grafico di f(x)
è sopra la tangente in (x0,f(x0))
per x < x0
e sotto per x > x0.
Se x0
è punto di flesso ed inoltre f′(x
0) = 0,
allora si dice che x0
è punto di flesso a tangente orizzontale
Riassumendo
Teorema 154 Sia x0 ∈ (a,b)
e sia f(x) ∈ C3(a,b).
Se f(2)(x
0) = 0
mentre f(3)(x
0)≠0
allora x0
è punto di flesso. Il flesso è ascendente se f‴(x0) > 0,
discendente se f‴(x0) < 0.
Naturalmente, può accadere che anche f(3)(x
0)
sia nulla. Cosìcome fatto per gli estremi, si possono guardare (se esistono) le
derivate successive e si ha:
Teorema 155 Se la prima derivata non nulla di f(x)
in x0
di ordine maggiore di 1
è di ordine dispari, la funzione ha punto di flesso in x0.
Il flesso è ascendente se tale derivata è positiva, discendente altrimenti.
5.4 Alcuni esercizi
- Sia F(x0) = 0,
con F(x)
primitiva di f(x).
Si è visto (al Teorema 140) che f(x) = o(x − x0)n
per x → x0
implica che F(x) = o(x − x0)n+1.
Si vuol sapere se ciò vale solamente per n
intero, o se vale per qualsiasi esponente positivo (ovviamente restringendosi
alle x > x0).
- (⋆)
Ancora con riferimento al Teorema 140: supponiamo di sapere che
f(x) = o(x − x0)n
per x → x0.
Mostrare su un esempio che in generale non vale f′(x) = o(x − x
0)n−1
per x → x0
(un esempio si trova all’esercizio 11 del Cap. 3).
- Per x → +∞
sia f(x) = o(g(x)).
Siano F(x)
e G(x)
primitive rispettivamente di f(x)
e di g(x).
Supponiamo che lim x→+∞F(x) = lim x→+∞F(x) = +∞.
Si chiede se vale F(x) = o(G(x)).
- Trovare esempi di funzioni diverse
f(x) e
g(x), di classe
C1(ℝ), i cui grafici
hanno un punto (x0,y0)
comune e tali che valga una delle ulteriori proprietà seguenti:
- x0
è punto di massimo oppure di minimo per ambedue le funzioni;
- x0
sia punto di massimo per l’una e di minimo per l’altra;
- una delle due sia convessa e l’altra concava.
(⋆) Può
essere che x0
sia asintoto verticale per una delle due funzioni?
- Sia f(x)
derivabile su (a, +∞)
e illimitata. Si mostri che se esiste un asintoto obliquo
y = mx + n allora
m = lim x→+∞f′(x).
- (⋆)
Sia y = mx + n
asintoto obliquo destro della funzione derivabile
f(x). E’ vero che
deve esistere lim x→+∞f′(x)?
- (⋆) Si consideri la
funzione cosídefinita: f(n) = n;
f(n + 1∕n2) = (n + 1∕n).
Negli altri punti il grafico si ottiene congiungendo con segmenti i punti
(n,f(n)) ed
((n + 1),f(n + 1)). Si
tracci il grafico della funzione. Questa funzione è derivabile salvo che nei punti
n ed
n + 1∕n2. Si dica
se esiste lim x→+∞f′(x).
Si illustri qualitativamente come sia possibile modificare il grafico di questa
funzione, in modo da rispondere alla domanda 6.
- Si mostri un esempio di funzione monotona la cui derivata prima ammette zeri. E’ possibile
che f′(x) ammetta
infiniti zeri su ℝ?
E su un intervallo limitato?
- Si sa che f(x) è
continua in x = 0
e che per x → 0
vale
f(x) = 5 + 3x2 + 2x4 + o(x4).
Si noti che questa funzione è derivabile per
x = 0
(Teorema 96) ma che l’espressione scritta può non essere una formula di Taylor, perché la
f(x) potrebbe non essere
derivabile per x≠0. Ciò
nonostante, si provi che 0
è punto di minimo locale della funzione.
- (⋆) Sapendo
solamente che f(x)
è continua in 5
e che per x → 5
vale
f(x) = 3 + 2(x − 5) − 7(x − 5)9 + o(x − 5)9,
può dedursi che x0 è
punto di flesso di f(x)?
Anche se domf(x) = [−1, 5]?
- Le due funzioni f(x)
e g(x) siano
di calsse C4(ℝ)
e per x → x0
valga
f(x) − g(x) = 4(x − x0)2 + o(x − x
0)2.
Cosa può dedursi sulle tangenti alle due funzioni? E se invece
f(x) − g(x) = 3 + 4(x − x0)2 + o(x − x
0)2
cosa può dedursi sulle tangenti?
- Trovare una coppia di funzioni derivabili su
ℝ,
tali che
lim x→0f′(x) = lim
x→0g′(x)
ma tali che nessuna retta sia tangente ad ambedue le funzioni.
- (⋆)
Talvolta si trova la seguente come definizione di flesso: la funzione derivabile
f(x) ha flesso
in x0
se il grafico traversa la tangente nel punto
(x0,f(x0)).
Dire se questa definizione e quella data al paragrafo 5.3.2 si equivalgono.
Si consideri la funzione all’esercizio 47 del Capitolo 1. Si dica se
x0 = 0
è punto di flesso per questa funzione, per la definizione appena data, per la
definizione al paragrafo 5.3.2, o per ambedue.
- Sia f(x) una funzione
di classe C3
con f‴(x0)≠0.
Mostrare che le due definizioni di punto di flesso, quella del paragrafo 5.3.2 e
quella dell’esercizio 13, coincidono.
- Sia f(x) = x2 se
x ∈ ℚ, ed
f(x) = −x2 altrimenti. Mostrare
che il punto x0 = 0
è punto critico, ossia che la funzione è derivabile in
x0 = 0,
con derivata uguale a zero, ma che il punto
x0 = 0
non è né punto di massimo, né punto di minimo, né punto di
flesso.
- Calcolare
lim x→+∞e−2x + 5x + cos x
sin x − x − log x .
Verificare se questa funzione verifica o meno le condizioni del teorema di
l’Hospital e studiare il limite del quoziente delle derivate.
Capitolo 6
Ricapitolazioni
Il Trònfero s’ammalvola in
verbizie
incanticando sbèrboli giocaci
sbramìna con solènnidi e
vulpizie
tra i tavoli e gli ortèdoni fugaci.
Fosco Maraini, Via Veneto, in Gnòsi delle
Fànfole.
In questo capitolo ricapitoliamo alcuni dei concetti fondamentali incontrati fino ad ora.
Ossia, ricapitoliamo i concetti relativi alle successioni, incontrati in particolare nei
capitoli 1 e 2. La ricapitolazione relativa alle funzioni si otterrà mostrando come i
concetti studiati si possano usare per tracciare qualitativamente i grafici di funzioni.
Naturalmente, definizioni e teoremi vanno studiati ciascuno nel proprio
capitolo.
6.1 le successioni
Ricordiamo che ℕ
indica l’insieme dei numeri naturali (incluso o meno
0, come
generalmente si deduce dal contesto) e che una successione è una funzione il cui dominio
è ℕ.
Il simbolo usato per indicare una successione, invece di
f(n), è
(fn) oppure
{fn}. Quando,
come spesso accade, si intende che la successione prenda valori sull’asse delle ascisse,
scriveremo (xn)
oppure {xn}.
Il simbolo {xn}
è ambiguo perché indica sia la successione, ossia la funzione
n↦xn,
che l’insieme dei numeri xn,
ossia l’immagine della successione. Il significato va capito dal contesto.
Il grafico di una successione è l’insieme delle coppie
(n,xn),
che si rappresenta sul piano cartesiano come nell’esempio della
figura 6.1, a sinistra. Si noti che in questa figura abbiamo indicato con
n l’asse delle
ascisse e con x
quello delle ordinate, per coerenza con il simbolo
{xn} usato per
la successione. Quest’esempio aiuta anche a capire la differenza tra i due significati del
simbolo {xn}.
La figura 6.1, a sinistra riporta il grafico della funzione
{xn}
mentre a destra ne riporta l’immagine, ossia l’insieme
{xn}.
figure 6.1: Successione e immagine: II grafico della successione
(
n
,
(
-
1
)
n
n
)
è l'insieme dei punti del piano cartesiano
(
1
,
-
1
)
,
(
2
,
1
2
)
,
(
3
,
-
1
3
)
,
(
4
,
1
4
)
,
…
L'immagine della successione è l'insieme dei punti sulla retta
-
1
,
1
2
,
-
1
3
,
1
4
,
…
Grafico della successione
(
(
-
1
)
N
/
n
)
 La sua immagine
La sua immagine 
In pratica però tracciare il grafico di una successione non è molto utile perché
di una successione interessa il “comportamento asintotico”, ossia il comportamento
per n → +∞ e
questo non si vede disegnando pochi punti del grafico. Una successione è crescente
se n > m
implica xn ≥ xm
(se n > m
implica xn > xm
la successione si dice strettamente crescente). Si diano le definizioni di successione
decrescente e strettamente decrescente. Una successione strettamente monotona
(crescente o decrescente) è una trasformazione iniettiva e quindi invertibile.
Gli unici limiti che possono studiarsi per una successione sono i limiti per
n → +∞. In
particolare una successione si dice
- regolare se lim n→+∞xn
esiste, uguale a +∞,
a −∞
oppure ad l ∈ ℝ.
- altrimenti, la successione si dice indeterminata o oscillante
Le definizioni di limite di una successione sono state studiate al paragrafo 2. Dato che
l’unico caso di limite che può studiarsi per una successione è quello per
n → +∞, invece di scrivere
lim n→+∞xn, si può scrivere
piuù brevemente lim xn.
Infine, ricordiamo che per le successioni vale il teorema delle funzioni monotone, che
può enunciarsi come segue:
Teorema 156 Ogni successione monotona è regolare e precisamente vale:
- se la successione {xn}
è crescente,
lim xn = sup{xn};
- se la successione {xn}
è decrescente,
lim xn = inf{xn}.
Per interpretare l’enunciato di questo teorema, è importante aver capito i due significati diversi
della notazione {xn}.
Infine, ricordiamo il limite notevole
lim 1 + 1
nn = e.
Combinando questo limite col teorema sui limiti di funzioni composte, si trova:
|
lim 1 + a
nn = ea, lim 1 −1
nn = lim 1 + 1
n−n = 1
e.
|
6.2 Studi di funzione
Si chiama “studio di funzione” il processo che conduce a tracciare qualitativamente
il grafico di una funzione, individuandone dei punti particolarmente significativi.
Nel fare ciò, si devono usare tutte le nozioni che abbiamo incontrato fino ad ora e
conviene procedere con un certo metodo. Elenchiamone i punti salienti e poi
commentiamoli.
-
- A) il primo passo consiste nel determinare il dominio della funzione.
-
- B) si determinano eventuali simmetrie e periodicità
-
- C) Determinazione dei limiti (per x
tendente agli estremi del dominio o ad altri punti notevoli) e degli
eventuali asintoti.
-
- D) Si studia quindi la continuità della funzione, identificando gli eventuali
punti di discontinuità.
-
- E) Si studia la derivabilità della funzione, individuando gli eventuali punti
di non derivabilità.
-
- F) Si determinano gli intervalli di monotonia ed i punti di estremo della
funzione.
-
- G) Si studia la convessità della funzione.
NOTA IMPORTANTE In
un compito d’esame usualmente viene proposta una funzione e vengono
richieste solamente alcune delle proprietà del grafico. Per esempio, lo
studio della convessità potrebbe non essere richiesto. Ciò non solo
perché è diffcile, ma anche perché si valuta che porti via del tempo da
dedicare invece ad altre domande. Per questo si sconsiglia di fare studi non
richiesti. Infatti:
- parti in più oltre a quelle richieste non hanno punteggio, ma gli
eventuali errori possono venir valutati;
- parti in più di una parte del compito non compensano eventuali
parti non svolte. Il punteggio delle parti non svolte non viene
comunque attribuito.
Il grafico della funzione va tracciato qualitativamente solo sulla base
degli elementi richiesti, ed è importante che sia coerente con i
risultati trovati, anche se sono sbagliati. Un grafico corretto
ma non coerente con gli errori fatti viene considerato incoerente
e penalizzato. Talvolta certi errori rendono impossibile tracciare
un grafico (per esempio, se si trova che la funzione decresce per
x > 0
e contemporaneamente che diverge positivamente per
x → +∞ il
grafico non può farsi). In questo caso una delle informazioni
trovate è sbagliata. Se possibile, conviene correggerla. Se non c’è
tempo di correggerla, al momento di tracciare il grafico, NOTARE
ESPLICITAMENTE l’incoerenza dei risultati trovati, dicendo quali si
conservano nel tracciare il grafico. Ciò per evitare penalizzazioni dovute al
grafico incoerente. Inoltre, un compito d’esame può fare altre domande,
per esempio di individuare il numero delle intersezioni tra il grafico
tracciato e certe famiglie di curve, per esempio rette; di dedurre dal
grafico tracciato quello di altre funzioni (per esempio, dal grafico di
f(x) quello
di 1∕f(x) o
di |f(x)|).
Ora commentiamo i vari passi.
-
- A) Determinazione del dominio della funzione. Ricordiamo che questo è
un problema puramente scolastico. Il dominio della funzione fa parte
della descrizione del processo fisico che si intende studiare, e quindi
è assegnato insieme alla funzione stessa. Invece, come puro esercizio
scolastico, si intende che la funzione è definita in ciascuno dei punti nei
quali possono effettuarsi le operazioni mediante le quali viene assegnata.
-
- B) Simmetrie e periodicità. Ricordiamo che una funzione è pari o dispari
se il suo dominio è simmetrico rispetto all’origine ed inoltre è pari se
f(x) = f(−x)
(grafico simmetrico rispetto all’asse delle ordinate) ed è dispari se
f(x) = −f(−x)
(grafico simmetrico rispetto all’origine). Se una funzione è pari o dispari
ci si può limitare a studiare la funzione per x > 0
e ottenerne il grafico su tutto il dominio usandone la simmetria.
Non va dimenticato di studiare esplicitamente la natura che il punto
x = 0
ha rispetto alla funzione (continuità, derivabilità, punto di estremo…).
Una funzione è periodica se esiste T > 0
tale che f(x) = f(x + T).
Il numero T
si chiama “periodo” della funzione. Se esiste un minimo periodo
che è strettamente positivo, generalmente è tale numero che si
chiama “periodo”. Naturalmente, una funzione periodica ha dominio
illimitato sia superiormente che inferiormente ed è priva di limite per
x → +∞
ed x →−∞,
salvo il caso in cui sia costante. Se una funzione è periodica di periodo
T,
ci si può limitare a studiarne la restrizione all’intervallo [0,T]
e quindi tracciarne il grafico per periodicità (senza dimenticare di
studiare la continuità, derivabilità, massimi o minimi…in 0
e in T).
-
- C) Determinazione dei limiti e degli asintoti. Se il dominio è illimitato, si
calcolano i limiti per x → +∞
e per x →−∞.
Se uno di questi limiti è finito, e vale l,
la retta y = l
si chiama “asintoto orizzontale” (destro, sinistro oppure bilatero). Se
invece la funzione è un infinito del primo ordine rispetto all’infinito di
confronto x,
può esistere o meno un “asintoto obliquo”. Questo va determinato. Si
calcolano quindi i punti x0
tali che uno almeno dei due limiti
lim x→x0±|f(x)| = +∞.
In tal caso, la retta x = x0
si chiama “asintoto verticale” per la funzione. Ricordiamo che se
x = x0
è un asintoto verticale, il punto x0
può appartenere o meno al dominio della funzione.
-
- D) Continuità della funzione, ed eventuali punti di discontinuità. Conviene
anche studiare se la funzione ammette o meno estensione continua a
punti che non appartengono al dominio. La funzione è continua in
x0
se
lim x→x0f(x) = f(x0).
Può accadere che f(x)
non sia definita in x0
ma che esista
lim x→x0f(x) = l ∈ ℝ.
In tal caso, la funzione
g(x) = f(x) sex≠0
l sex = 0
è continua in x0
e si chiama l’estensione per continuità di f(x)
ad x0.
Per esempio, la funzione
f(x) = e−1∕x2
non è definita in 0
ma può essere estesa per continuità a 0
perché
lim x→0e−1∕x2
= 0.
Naturalmente, può accadere che si possa definire un’estensione della
funzione che è continua o solo da destra o solo da sinistra, come accade
per la funzione
f(x) = e1∕x.
Questa funzione è priva di limite per x → 0
e si ha
lim x→0−f(x) = 0, lim x→0+f(x) = +∞.
L’estensione
g(x) = f(x) sex≠0
0 sex = 0
non è continua in 0, ma è
continua da sinistra in 0.
Se f(x) non è
continua in x0
si possono avere i tre casi seguenti:
- discontinuità eliminabile: se il limite
lim x→x0f(x) = l ∈ ℝ,
con l≠f(x0).
Un esempio è in figura 6.2, a sinistra.
- discontinuità di prima specie o salto se ambedue i
limiti direzionali seguenti esistono finiti, ma diversi tra
loro. Non si esclude che uno dei due possa essere uguale ad
f(x0),
si veda la figura 6.2, a destra.
- discontinuità di seconda specie ogni altro caso. Esempi sono
in figura 6.3.
-
- E) Si studia la derivabilità della funzione ed eventuali punti di non derivabilità.
Supponiamo che esista, finito o meno, il limite seguente:
lim x→x0f(x) − f(x0)
x − x0
Si hanno i due casi seguenti:
Supponiamo ora che il limite (6.1) non esista, ma che esistano, finiti o meno,
ambedue i limiti direzionali
lim x→x0−f(x) − f(x0)
x − x0 = f−′(x
0), lim x→x0+f(x) − f(x0)
x − x0 = f+′(x
0).
I due limiti si chiamano derivate direzionali (destra o sinistra) in
x0.
Si ha:
- se la derivata destra è finita, la funzione è continua in x0
da destra; analoga affermazione per la derivata sinistra. Se una
derivata direzionale è +∞
oppure −∞,
la funzione può essere continua o meno.
- Se le due derivate direzionali sono ambedue finite e diverse tra loro, il punto
(x0,f(x0))
si dice punto angoloso e le due rette
|
y = f(x0) + f−′(x
0)(x − x0),
y = f(x0) + f+′(x
0)(x − x0)
|
si chiamano le tangenti al grafico di
f(x)
da sinistra o da destra in x0
(più correttamente, sono le tangenti in
(x0,f(x0))
ai grafici delle restrizioni di f(x)
a x ≤ x0,
rispettivamente a x ≥ x0).
Un esempio è in figura 6.6, a sinistra.
- se la funzione è continua in
x0
e se le due derivate direzionali in
x0 sono una
+∞ e l’altra
−∞, il punto
(x0,f(x0)) si dice cuspide
La retta x = x0
si dice ancora tangente al grafico in
(x0,f(x0)).
Un esempio è in figura 6.8, a destra mentre la figura 6.6
mostra due casi in cui il rapporto incrementale ha limite
+∞.
- Infine, supponiamo che f(x) sia
definita su un intervallo [a,b]
e x0 = a
(oppure x0 = b).
Se esiste la derivata, rispettivamente destra o sinistra, in
x0,
si può ancora parlare di tangente al grafico della funzione in
(x0,f(x0)).
Naturalmente, se la derivata direzionale è
+∞ oppure
−∞
allora dovremo preventivamente richiedere che la funzione sia continua in
x0.
Osservazione 157 Supponiamo f(x)
definita su (a,b),
continua in x0 ∈ (a,b).
Supponiamo che le due derivate direzionali in x0
esitano e siano ambedue +∞
oppure −∞.
Allora, x = x0
è tangente verticale al grafico di f(x)
nel punto (x0,f(x0)).
Il grafico taglia la tangente nel solo punto (x0,f(x0)),
perché la funzione è univoca. Quindi, il grafico sta da una parte
della tangente per x < x0
e dall’altra per x > x0.
Se accade che la funzione è convessa da una parte di x0
e concava dall’altra, il punto x0
si chiama flesso a tangente verticale Questo caso è illustrato nella
figura 6.6, a destra. ■
Lo studio della derivabilità nei punti in cui non si possono applicare le
formule di derivazione, si fa studiando esplicitamente il limite del rapporto
incrementale, generalmente mediante il Teorema di L’Hospital.
-
- F) Gli intervalli di monotonia ed i punti di estremo della funzione. Gli intervalli di
monotonia si determinano studiando il segno della derivata prima e quindi
conducono alla risoluzione di opportune disequazione. Lo studio della monotonia
può portare ad identificare immediatamente alcuni punti di estremo: quei punti
x0
nei quali la funzione è continua e monotona di senso opposto dalle due
parti del punto. In generale, i punti di estremo della funzione vanno cercati
tra i punti in cui si annulla la derivata prima e tra i punti nei quali la funzione
non è derivabile (inclusi gli estremi del dominio, se la funzione vi è
definita). Alternativamente, invece di dedurre le proprietà di estremo dallo
studio della monotonia, si può studiare il segno delle derivate successive
(ma spesso ciò conduce a calcoli più complessi e inoltre non si
può fare negli estremi del dominio e nei punti in cui le derivate non
esistono).
-
- G) Convessità della funzione. Quando la funzione è derivabile, conviene studiare la
monotonia della derivata prima, ossia il segno della derivata seconda. Supponiamo ora
x0 ∈ (a,b) e che esista
f′(x
0). Confrontiamo il
grafico di f(x) con la
retta tangente in (x0,f(x0)).
Si hanno tre casi:
- esiste un intorno di x0
in cui vale
f(x) ≥ f(x0) + f′(x
0)(x − x0).
In tal caso la funzione si dice convessa in x0
- esiste un intorno di x0
in cui vale
f(x) ≤ f(x0) + f′(x
0)(x − x0).
In tal caso la funzione si dice
concava in x0
La figura 6.7 mostra il grafico di una funzione che è convessa in
alcuni punti, concava in altri.
- esiste un I
intorno di x0
tale che
|
x ∈ I,x ≤ x0⇒f(x) ≥ f(x0) + f′(x
0)(x − x0),
x ∈ I,x ≥ x0⇒f(x) ≤ f(x0) + f′(x
0)(x − x0)
|
(o le analoghe, con i versi delle disuguaglianze a
destra scambiati tra loro). In tal caso si dice che
x0
è “punto di flesso”. Un esempio è in figura 6.8, a sinistra.
La figura 6.8, a destra, mostra una funzione che cambia di
concavità in corrispondenza di un punto che non è di flesso,
perché in tale punto non esiste la tangente al grafico della
funzione.
Naturalmente, può darsi che nessuno dei casi descritti si verifichi. Si
consideri l’esempio della funzione
f(x) = x2 sin(1∕x) sex≠0
0 sex = 0.
Capitolo 7
Numeri complessi
Non è per la sua cultura che lo amo—no, non è per quello.
E’ un autodidatta; in realtà conosce una quantità di cose,
solo che non stanno cosìcome le sa lui. Diario di Eva, Il
diario di Adamo ed Eva di Mark Twain
In questo capitolo introduciamo le proprietà essenziali di una nuova classe di numeri
che si chiamano numeri complessi Per quanto storicamente falso, conviene pensare
ai numeri complessi come introdotti per risolvere l’equazione
x2 + 1 = 0,
ovviamente priva di soluzioni in ℝ.
7.1 La definizione dei numeri complessi
Si riferisca il piano ad un sistema di coordinate cartesiane
ortogonali di origine in un
punto O. In questo modo, un
punto P viene identificato
dalle sue coordinate x
(ascissa) ed y
(ordinata) e viene indicato in vari modi, per esempio
P(x,y). I
numeri complessi sono i punti del piano cartesiano dotati di due operazioni che
hanno un significato fisico che vedremo, ma la notazione che si usa per indicare i
numeri complessi è diversa da quella usuale della geometria analitica o della fisica.
La seconda componente, ossia l’ordinata, si identifica mediante un “fattore”
usualmente
indicato con i,
scritta indifferentemente prima o dopo. E il punto
P di
coordinate x
ed y si
indica con x + iy
o anche x + yi.
Questa notazione permette di identificare immediatamente l’ordinata del punto, che è
y, e quindi anche
l’ascissa, che è x.
Dunque, l’ordine in cui esse vengono scritte non ha influenza e lo stesso numero
complesso può rappresentarsi indifferentemente
x + iy = x + yi = yi + x = iy + x.
Inoltre, se una delle due coordinate è nulla essa si sottintende e quindi
xindica x + i0,iyindica 0 + iy.
Se ambedue le coordinate sono nulle, ossia se il punto corrisponde all’origine, esso si
indica con 0.
Si noti in particolare: |
1 indica 1 + i0 e si chiama unità dei numeri complessi;
i indica 0 + 1i e si chiama unità immaginaria
|
Inoltre, i numeri iy
si chiamano numeri immaginari (talvolta “immaginari puri”) e quindi
l’asse delle ordinate si chiama anche asse immaginario I numeri
x = x + i0 si
chiamano numeri complessi reali e l’asse delle ascisse si chiama anche asse reale Nel
contesto dei numeri complessi, i termini “ascissa” ed “ordinata” vengono sostituiti dai
termini parte reale e parte immaginaria Inoltre, i numeri complessi si indicano spesso con
le lettere z,
u,
v,
w ed è più frequente
usare le lettere a
e b (per esempio)
invece di x
ed y.
Ossia, scriveremo
z = a + ib
e useremo le notazione seguenti per la parte reale e la parte immaginaria:
ℜez = a,ℐmz = b.
Si noti che “parte reale” e “parte immaginaria” sono ambedue numeri reali. Se
z = a + ib, il simbolo
−z indica il numero
−a + i(−b) che si scrive più
semplicemente −a − ib.
Ossia,
−z = −a − ib.
L’insieme dei numeri complessi si chiama anche piano complesso o
piano di Argand-Gauss I numeri complessi si chiamano anche i “punti”
del piano complesso. Per esercizio, si indichi un numero complesso
z sul piano
complesso, e quindi −z.
L’insieme dei numeri complessi, dotato delle operazioni che vedremo, si indica col simbolo
ℂ. La
rappresentazione a + ib
si chiama rappresentazione algebrica dei numeri complessi. E’ importante anche una
seconda rappresentazione, che si chiama “trigonometrica”.
Rappresentazione trigonometrica dei numeri complessi Consideriamo
un’altra rappresentazione dei punti del piano cartesiano, e quindi anche dei punti
del piano complesso, che si chiama la rappresentazione polare Si congiunga il punto
P(x,y), ossia il numero
complesso z = x + iy,
con l’origine delle coordinate. Si trova un segmento la cui lunghezza è
r = x2 + y2.
Il numero r
si chiama il modulo del numero complesso. Il segmento fa un’angolo
𝜃 con
l’asse reale positivo.
Il numero 𝜃
si considera positivo se il semiasse reale positivo
gira in senso antiorario per sovrapporsi al segmento
PO,
orientato da O
verso P;
negativo altrimenti.
Quest’angolo si chiama argomento o anomalia La coppia
(r,𝜃)
si chiama rappresentazione polare ad ogni coppia
(r,𝜃) corrisponde un
solo punto P.
Si noti però che la corrispondenza tra
P
e la sua rappresentazione polare non è biunivoca: l’angolo
𝜃
è determinato a meno di multipli di
2π
se r > 0.
Infatti,
(r,𝜃) e(r,𝜃 + 2π)
identificano il medesimo punto P.
Se r = 0,
tutte le coppie (0,𝜃)
identificano l’origine delle coordinate. Si ritrova
una corrispondenza biunivoca, ma solamente per
r > 0,
se si impone di scegliere 𝜃 ∈ [0, 2π).
L’argomento cosìscelto si chiama argomento principale
Noti r
e 𝜃, si
ha
x = r cos 𝜃,y = r sin 𝜃
e quindi il numero complesso x + iy
si scrive come
r cos 𝜃 + ir sin 𝜃
che usa scrivere come
r(cos 𝜃 + i sin 𝜃).
Si chiama questa la rappresentazione trigonometrica dei numeri complessi
7.2 Operazioni tra i numeri complessi
Per ora abbiamo descritto l’insieme dei numeri complessi. Descriviamo ora le
operazioni tra essi, che sono due: la somma e il prodotto (che daranno anche la
sottrazione e la divisione).
7.2.1 Somma di numeri complessi
E’ l’operazione di somma di vettori con la regola del parallelogramma, ossia essa si
fa sommando le componenti corrispondenti:
(a + ib) + (c + id) = (a + c) + i(b + d).
Si osservi che
- z + 0 = z
- z + (−z) = 0
- (v + z) + w = v + (z + w)
- z + w = w + z.
7.2.2 Il prodotto
Il prodotto di due numeri complessi si indica con
z ⋅ w (o anche
semplicemente come zw)
e si capisce meglio rappresentando i numeri in forma trigonometrica. Definiamo
[r(cos 𝜃 + i sin 𝜃)] ⋅ [ρ(cos ϕ + i sin ϕ)] = rρ cos(𝜃 + ϕ) + i sin(𝜃 + ϕ) .
Ossia, il prodotto opera in questo modo: prima si sommano gli argomenti, e quindi
il primo punto viene ruotato di tanto quanto è l’argomento del secondo, e poi
si fa il prodotto dei moduli. Per chi conosce un po’ di elettrotecnica: è
questa la forma che assume la legge di Ohm per le correnti alternate! Il
numero
1 = 1 + i0 = 1(cos 0 + i sin 0)
è l’elemento neutro rispetto al prodotto:
z ⋅ 1 = 1 ⋅ z = z
per ogni z ∈ ℂ.
Il numero w = 1∕z
deve verificare
wz = 1.
Quindi, se z = r(cos 𝜃 + i sin 𝜃),
1
z = 1
r cos(−𝜃) + i sin(−𝜃) = 1
r(cos 𝜃 − i sin 𝜃).
Definito il prodotto, si possono definire le potenze ad esponente intero:
z2 = z ⋅ z,z−1 = 1
z,z−2 = 1
z2,…
Il prodotto in notazione algebrica Usiamo i colori per distinguere un
numero complesso dall’altro: sia
z = a + ib,w = c + id
quando i due numeri sono rappresentati in notazione algebrica e, corrispondentemente
z = r cos 𝜃 + i sin 𝜃,w = ρ cos ϕ + i sin ϕ.
Dunque |
a = r cos 𝜃,b = r sin 𝜃,
c = ρ cos ϕ,d = ρ sin ϕ.
|
Il prodotto è: |
z ⋅w = r cos 𝜃 + i sin 𝜃 ⋅ρ cos ϕ + i sin ϕ
(rρ) cos(𝜃 + ϕ) + i sin(𝜃 + ϕ)
= (rρ) cos 𝜃 cos ϕ − sin 𝜃 sin ϕ + i sin 𝜃 cos ϕ + cos 𝜃 sin ϕ
= (r cos 𝜃)(ρ cos ϕ) − (r sin 𝜃)(ρ sin ϕ) + i (r sin 𝜃)(ρ cos ϕ) + (r cos 𝜃)(ρ sin ϕ)
= ac −bd + i ad + bc.
|
Abbiamo quindi la seguente formula per il prodotto di numeri complessi in
notazione algebrica: |
z ⋅w = a + ib ⋅c + id = ac −bd + i ad + bd.
| (7.1) |
Non è necessario ricordare questa formula, perché si può ottenerla
facilmente in questo modo: distribuiamo i prodotti sulle somme, ottenendo
|
a + ib ⋅c + id
= ac + ibd + aid + ibid
|
Ora si proceda con le usuali regole algebriche, scambiando i simbili
i nei
prodotti e raccogliendoli. Si trova |
a + ib ⋅c + id
= ac + ibc + aid + ibid
= ac + ibc + iad + (i ⋅ i)bd
= ac + i bd + ad + (i ⋅ i)bd.
|
Confrontiamo (7.1) con (7.1). Si vede che la seconda restituisce la prima
se ad
i ⋅ i = i2 si
sostituisce −1.
Infatti, con quest’ultima sostituzione si trova la formula del prodotto:
a + ib ⋅c + id = ac −bd + i ad + bc.
Segue da qui che le operazioni algebriche tra i numeri complessi si
fanno operando con le usuali regole algebriche, alle quali va aggiunta
l’ulteriore “regola”
i2 = −1.
7.3 Il coniugato
Sia z = a + ib = r(cos 𝜃 + i sin 𝜃). Il coniugato
del numero z
è il numero
z̄ = a − ib,
simmetrico di z
rispetto all’asse reale. In notazione trigonometrica,
z̄ = r(cos 𝜃 − i sin 𝜃).
Si noti che
zz̄ = r2 = |z|2.
I numeri z̄
e 1∕z
hanno i medesimi argomenti ma in generale modulo diverso. Si ha
z̄ = 1∕z
se e solo se |z| = 1,
ossia se e solo se il punto del piano
cartesiano che corrisponde al numero complesso
z
è sulla “circonferenza goniometrica”, ossia sulla circonferenza di raggio
1
e centro l’origine delle coordinate.
Il coniugato è utile per esempio per scrivere in modo semplice l’espressione di
1∕z in
rappresentazione algebrica:
1
z = 1
z z̄
z̄ = x − iy
|z|2 = x − iy
x2 + y2;
e quindi
w
z = wz̄
|z|2 .
Si verifica immediatamente che il coniugato di una somma è la somma dei
coniugati e il coniugato di un prodotto è il prodotto dei coniugati,
ossia,
z + w¯ = z¯ + w¯,z ⋅ w¯ = z¯ ⋅w¯.
Si suggerisce di verificare la regola relativa al prodotto sia usando la
rappresentazione algebrica che quella trigonometrica. Notiamo infine che se
z = a + ib,
ℜez = a = z + z̄
2 ,ℐmz = b = z −z̄
2i .
7.4 Radici di numeri complessi
Ricordiamo che la radice n–ma
di un qualsiasi numero z
è un numero w
che risolve l’equazione
wn = z.
Vogliamo studiare quest’equazione tra i numeri complessi. Ricordiamo il significato geometrico del
prodotto w ⋅ w: è quel
numero il cui modulo è |w|2
ed il cui argomento è il doppio dell’argomento di
w. In
generale, se
w = r(cos 𝜃 + i sin 𝜃)⇒wn = rn(cos n𝜃 + i sin n𝜃);
ossia, wn ha per
modulo |w|n e per
argomento n𝜃. In
particolare, se w≠0
allora wn≠0.
Dunque, l’equazione
wn = 0
ha la sola radice w = 0.
Sia invece
z = ρ(cos ψ + i sin ψ) = ρ cos(ψ + 2kπ) + i sin(ψ + 2kπ) ≠0.
Si ricercano numeri
w = r(cos 𝜃 + i sin 𝜃)
tali che
wn = zossiarn cos(n𝜃) + i sin(n𝜃) = ρ cos(ψ + 2kπ) + i sin(ψ + 2kπ) .
Quest’uguaglianza vale se e solo se rn = ρ,
ossia r = ρn
e inoltre
n𝜃 = ψ + 2kπ
ove k è un qualunque
numero intero. Dunque, 𝜃
deve essere uno dei numeri
𝜃 = ψ + 2kπ
n .
Sono questi infiniti argomenti ma, a causa della periodicità delle funzioni
sin 𝜃 e
cos 𝜃, solamente gli argomenti
che si ottengono per k = 0,
1,
…,
n − 1 danno valori
diversi di w.
Ricapitolando:
Geometricamente, le radici n–me
di z sono i vertici di un
poligono regolare di n
lati, i cui vertici giacciono sulla circonferenza di centro l’origine e raggio
|z|n. La
formula (7.2) talvolta si chiama anche formula di Moivre Torniamo ora
all’uguaglianza
cos n𝜃+i sin n𝜃 = cos 𝜃 + i sin 𝜃n = ∑
k=0n n k cos k𝜃 (i)n−k sin n−k𝜃.
Uguagliando parte reale ed immaginaria di queste formule, si trovano espressioni
per cos n𝜃 e
sin n𝜃, scritte combinando
solamente cos 𝜃
e sin 𝜃.
Anche queste formule si chiamano formule di Moivre Un fatto notevole
da notare è che i termini reali al membro destro devono avere
n − k pari e in tal caso
sin n−k𝜃 si esprime mediante
potenze (di ordine pari) di cos 𝜃,
ossia cos n𝜃
può rappresentarsi come combinazione di potenze di
cos 𝜃, senza far
intervenire sin 𝜃.
7.5 Esponenziale ad esponente complesso
Consideriamo un numero complesso non nullo, rappresentato in forma
trigonometrica
z = r(cos 𝜃 + i sin 𝜃).
Dato che r > 0,
si potrà scrivere
r = ea
(con a = log r).
Dunque avremo
z = ea(cos 𝜃 + i sin 𝜃).
Quest’uguaglianza suggerisce di definire
ei𝜃 = cos 𝜃 + i sin 𝜃
cosìche
z = eaei𝜃.
Definiremo poi
ea+i𝜃 = eaei𝜃
cosìche
z = ea+i𝜃.
Si è cosìdefinita l’esponenziale di esponente complesso, |
eα+i𝜃 = eα cos 𝜃 + i sin 𝜃
| (7.3) |
Questo è niente altro che un simbolismo diverso per la rappresentazione
trigonometrica di numeri complessi. Però, l’esponenziale di numeri complessi
cosìdefinita gode delle proprietà caratteristiche dell’esponenziale reale. Infatti,
siano z
e w due
numeri complessi non nulli,
z = r(cos 𝜃 + i sin 𝜃) ,w = ρ(cos ϕ + i sin ϕ) .
I moduli sono positivi e quindi si può scrivere
r = eα,ρ = eβ.
Dunque, il prodotto è
zw = eαeβ cos(𝜃 + ϕ) + i sin(𝜃 + ϕ) = eα+β+i(𝜃+ϕ).
Si trova quindi
eα+i𝜃eβ+iϕ = e(α+β)+i(𝜃+ϕ).
Ed inoltre,
e0 = e0+i0 = e0 cos 0 + i sin 0 = 1 + i0 = 1.
Ossia, le proprietà cruciali dell’esponenziale reale continuano a valere per
l’esponenziale complesso. La (7.3) definisce una funzione che ad un numero complesso
associa un numero complesso, che si chiama l’esponenziale di numeri complessi. Le
sue proprietà essenziali sono:
- |ei𝜃| = cos 2 𝜃 + sin 2 𝜃 = 1;
- |eα+i𝜃| = |eαei𝜃| = eα.
In particolare, l’esponenziale di numeri complessi non si annulla;
- e0 = 1;
- eα+i𝜃eβ+iϕ = e(α+β)+i(𝜃+ϕ);
- eα+i0 = eα + i0;
Queste proprietà sono le ovvie estensioni delle corrispondenti proprietà dell’esponenziale
di numeri reali. Le seguenti proprietà invece non hanno analogo tra i numeri reali:
- eα+iβ¯ = eα−iβ;
- e(α+iβ)+2πi = eα+iβ.
L’ultima proprietà mostra che l’esponenziale di numeri complessi è periodica di
periodo 2πi.
E quindi la definizione di logaritmo tra i numeri complessi, che non trattiamo, sarà
alquanto delicata. Notiamo infine le formule seguenti: |
eiπ = e−iπ = −1,e2πi = 1,
eiπ∕2 = i, e−iπ∕2 = −i.
|
L’uguaglianza
e2πi = 1
si chiama formula di Eulero La (7.3), che è la rappresentazione trigonometrica
dei numeri complessi scritta in modo più compatto, è la forma più
semplice e maneggevole quando si debbano fare operazioni di prodotto,
quoziente, potenza e radice di numeri complessi. Per questo gli si dà il nome di
rappresentazione esponenziale dei numeri complessi. Si noti che il numero
0 = 0 + i0
è l’unico numero complesso che non ha rappresentazione
esponenziale, ossia non si può scrivere in forma
ez. Infatti,
l’esponenziale non si annulla mai. Usando la rappresentazione esponenziale dei numeri complessi,
le radici n-me
di
eα+i𝜃
sono rappresentano come
e(α+i𝜃)∕ne(2kπi)∕n,0 ≤ k ≤ n − 1
(ed ovviamente k
intero). I numeri
𝜖k = e(2kπi)∕n,0 ≤ k ≤ n − 1
sono le n
radici n-me
di 1.
7.6 Continuità e derivate
Consideriamo ora una funzione a valori complessi di una variabile reale che indichiamo
con t:
t↦z(t) = f(t) + ig(t).
Supponiamo che t
appartenga ad un intervallo (a,b).
Limiti e continuità si definiscono per componenti, ossia, per la definizione di
limite,
lim t→t0z(t) = lim t→t0 f(t) + ig(t) = lim t→t0f(t) + i lim t→t0g(t) .
E quindi, in particolare, z(t)
è continua in t0
se e solo se sia f(t)
che g(t) lo
sono. La derivata si definisce come il limite del rapporto incrementale,
|
lim h→0z(t0 + h) − z(t0)
h = lim h→0 f(t0 + h) + ig(t0 + h) −f(t0) + ig(t0)
h
= lim h→0f(t0 + h) − f(t0)
h + i lim h→0 g(t0 + h) − g(t0)
h .
|
Dunque, anche la derivata si definisce per componenti e
z(t) è derivabile se e solo
se sono derivabili sia f(t)
che g(t).
In tal caso si ha:
sez(t) = f(t) + ig(t) alloraz′(t) = f′(t) + ig′(t).
A noi interessa calcolare la derivata dell’esponenziale. Per essa vale una forma in
tutto analoga a quella che si ha per l’esponenziale reale:
Teorema 158 Vale:
d
dtez0t = z
0ez0t.
Dim. Sia
z0 = a + ibcosìcheez0t = eat(cos bt + i sin bt).
Dunque,
ez0t = f(t)+ig(t), con f(t) =eat cos bt
g(t) =eat sin bt.
Calcoliamo la derivata della parte reale e della parte immaginaria: |
f′(t) = eat a cos bt − b sin bt,
g′(t) = eat a sin bt + b cos bt.
|
Quindi: |
d
dtez0t = f′(t) + ig′(t) = eat a cos bt − b sin bt + ieat a sin bt + b cos bt
(a + ib) ⋅eat cos bt + i sin bt = z
0ez0t. ■
|
7.7 Il teorema fondamentale dell’algebra
L’esistenza delle radici permette di risolvere le equazioni della forma
zn + a = 0
ove a è il
termine noto e z
è l’incognita: Quest’equazione ha la sola soluzione nulla se
a = 0. Altrimenti
ammette n
soluzioni. Consideriamo ora l’equazione che si ottiene uguagliando a zero un generico
polinomio
|
0 = anzn + a
n−1zn−1 + ⋯a
1z + a0 = ∑
r=0na
rzr,a
n≠0.
| (7.4) |
Se n = 1
oppure n = 2
allora quest’equazione ammette soluzioni (rispettivamente, una soluzione oppure
due soluzioni) ed esiste una formula per rappresentare le soluzioni. Formule
risolutive per le equazioni di terzo e quarto grado esistono, e sono state scoperte nel
XVI secolo. Naturalmente, in generale le soluzioni sono numeri complessi. Tra il
XVIII e il XIX secolo è stato provato che non esistono formule risolutive per
equazioni di grado superiore al quarto (espresse mediante un numero finito di
operazioni algebriche). Ciò nonostante, è stato provato il teorema seguente:
Teorema 159 (fondamentale dell’algebra) Ogni equazione di grado
n > 0
ammette almeno una soluzione complessa.
Ora, si sa che se z = z0
risolve l’equazione (7.4) allora si può scrivere
anzn + a
n−1zn−1 + ⋯a
1z + a0 = (z − z0) ∑
r=0n−1b
rzr.
ossia, z − z0
divide il polinomio. Il teorema 159 può ora applicarsi al polinomio
∑
r=0n−1b
rzr.
Se n > 1 si trova
un numero z1
che annulla questo polinomio e che quindi risolve (7.4). Ovviamente, può accadere
che sia z1 = z0.
Iterando questo procedimento, si viene a scrivere
∑
r=0na
rzr = (z − z
0)r0
(z − z1)r1
⋯(z − zν)rν
e |
n = r1 + r2 + ⋯ + rn.
| (7.5) |
I numeri zj, che sono
tutte e sole le soluzioni di (7.4) si dicono radici o anche zeri del polinomio e si dice che la radice
zj di (7.4), equivalentemente
lo zero zj del polinomio,
ha molteplicità rj,
ove rj è l’esponente
del fattore (z − zj).
La (7.5) vuol dire che il numero totale delle radici, ciascuna contata
secondo la propria moltaplicità, è uguale al grado del polinomio.
7.7.1 Polinomi a coefficienti reali
Ricordiamo queste proprietà dell’operazione di coniugio: il coniugato di una
somma è la somma dei coniugati e il coniugato di un prodotto è il
prodotto dei coniugati. Ossia
z + w¯ = z¯ + w¯,z ⋅ w¯ = z¯ ⋅w¯.
Dunque, zk¯ = (z¯)k = z¯k.
Ricordiamo inoltre che un numero è reale se e solo se coincide col suo coniugato.
Consideriamo ora un polinomio a coefficienti reali
∑
k=0na
kzk
e supponiamo che esso si annulli in z0,
0 = ∑
k=0na
kz0k.
Prendendo i coniugati dei suoi membri, e notando che
0 ̄ = 0, si
trova
0 = ∑
k=0nā
kz̄0k = ∑
k=0na
kz̄0k.
Ossia, anche z̄0
è uno zero del polinomio, che pertanto è divisibile per il trinomio a coefficienti
reali
(z − z0)(z −z̄0) = z2 − (2ℜez
0)z + |z0|2.
Dunque,
Teorema 160 Sia P(z)
un polinomio a coefficienti reali e sia z0
un suo zero di molteplicità r.
In tal caso, anche z0¯
è uno zero di P(z),
della medesima moltiplicità r.
Di conseguenza, le radici non reali di un polinomio a coefficienti reali vengono a
coppie, e quindi esse sono in numero pari. Ricordiamo ora che il numero totale
delle radici di un polinomio è il grado del polinomio, e quindi un polinomio di
grado dispari ha un numero dispari di radici. Di conseguenza, se i coefficienti di un
polinomio di grado dispari sono reali, almeno una delle sue radici deve essere
reale:
Teorema 161 Il numero delle radici reali di un polinomio di grado dispari e
a coefficienti reali è dispari. In particolare, ogni polinomio a coefficienti reali
di grado dispari ha almeno una radice reale.
Questo risultato si è già provato in altro modo, si veda il Corollario 114.
7.7.2 Il metodo di completamento dei quadrati
E’ utile ricordare come si ottiene la formula risolutiva di |
az2 + bz + c = 0 cona≠0.
| (7.6) |
Si nota che quest’equazione si sa risolvere se
b = 0. In questo caso le soluzioni
sono le due radici di −c∕a.
Se quest’equazione può ricondursi alla forma
allora essa è ancora immediatamente risolubile,
z = α + β
a
(si ricordi che la radice nel campo complesso prende due valori, e quindi questa
espressione rappresenta due soluzioni). Mostriamo che ogni equazione
della forma (7.6) può ricondursi alla forma (7.7) mediante il metodo del
completamento dei quadrati Prima di tutto si nota che risolvere (7.6) equivale a
risolvere
z2 + 2 b
2az + c
a = 0.
Vogliamo considerare il secondo addendo come il “doppio prodotto” di
z con
b∕2a. Dunque sommiamo
e sottraiamo (b∕2a)2.
Si trova
z + b
2a2 + c
a − b2
4a2 = 0.
E’ ora immediato vedere che l’equazione ammette due soluzioni, date da
− b
2a + − c
a − b2
4a2 = − b + b2 − 4ac
2a .
Si noti che non abbiamo scritto ±
di fronte alla radice perché per definizione la radice complessa prende due valori.
In contrasto con ciò, la radice positiva di un numero reale positivo si chiama
radice aritmetica
7.8 Alcuni esercizi
- Sul piano di Argand-Gauss si segni la posizione di un numero complesso
z.
Si segnino quindi i punti della lista seguente:
|
1∕z, z̄, −z̄,
1∕z̄, − 1∕z̄,iz,
iz¯, 1∕iz, 1∕iz¯.
|
Si consideri in particolare il caso in cui
z
giace su uno dei quattro semiassi coordinati.
- Sia z = a + ib,
w = c + id. Calcolare
z̄w.
chi conosce le espressioni in coordinate cartesiane ortogonali del prodotto
scalare e del prodotto vettoriale, noti come queste si ritrovano in questo
prodotto.
- Siano z = 1
2(1 + i) e
w = −z̄. Si identifichi
la posizione di z
e w
sul piano complesso, e si rappresentino i due punti
z + w e
z − w.
- Si calcolino i numeri in
per n intero
compreso tra 0
e 16.
- Usando la formula del binomio di Newton, si calcoli
(1 + i)9.
Si scriva quindi la rappresentazione trigonometrica del numero
(1 + i) e si usi questa
per calcolare (1 + i)9.
Rappresentare questo numero sul piano di Argand-Gauss.
- I numeri complessi z,
w abbiano
modulo 1 e
inoltre z abbia
argomento 2π∕3
mentre w abbia
argomento 4π∕3.
Sul piano complesso, si individui il punto
z + w. Si vuol sapere
se esiste u
tale che z + w + u = 0
e, nel caso affermativo, la sua posizione sul piano complesso.
- Si consideri un quadrato sul piano complesso, inscritto nella circonferenza
trigonometrica e i cui lati sono paralleli agli assi coordinati oppure alle
bisettrici degli assi. Si vuol sapere se i suoi vertici sono o meno radici di un
certo ordine di qualche numero.
- Il numero complesso z
abbia moduli 1 ed
argomento π∕12. Calcolare
un numero di cui z
è radice quarta. Quanti sono tali numeri?
- Scrivere in forma trigonometrica il numero
(cos π − i sin π∕2).
- (⋆)
Rappresentare sul piano di Argand-Gauss i numeri
(1∕2) cos π∕4
+i sin π∕4 n
e notare che essi si trovano su un numero finito di rette uscenti
dall’origine. Dire se accade un fatto analogo per i numeri
2 cos π∕7 + i sin π∕7 n e
2 cos(2π) + i sin(2π) n.
- (⋆) Si mostri che vale
l’uguaglianza (zw)2 = z2w2. Si consideri
quindi l’uguaglianza −4−9 = 36 = 6.
Dire se quest’uguaglianza è corretta. In generale discutere l’uguaglianza
zw = zw.
- Rappresentare sul piano complesso i numeri
z(t) = eit per
t ∈ ℝ. E se invece si
considerano i numeri z(t) = e−it?
- rappresentare sul piano di Argand-Gauss l’immagine della trasformazione
t↦teit.
- Calcolare le derivate prima e seconda della funzione
f(t) = e2it
e rappresentare sul piano di Argand-Gauss sia
f(t) che
f′(t) ed
f″(t).
- (⋆) Scrivere la formula
di McLaurin di ex
e sostituire ad iy
ad x.
Trovare le relazioni tra la formula ottenuta e le formule di McLaurin di
sin y e
cos y
(si ottiene una prima versione della “most remarkable formula in
mathematics”, come si esprime R. Feyman, nelle Feyman Lectures on
Physics).
- (⋆)
Sia z(t) = Aei(ωt+α),
w(t) = Bei(ωt+β). Dire se,
fissati A ed
ω, esitono
valori di α
e β tali
che z(t) + w(t) = 0 per
ogni t
(è possibile cancellare un suono mediante un altro suono? Si calcolino le
parti reali).
- (⋆)
Sia z(t) = eiωt,
w(t) = ei(ω+ν)t. Calcolare la
parte reale di z(t) + w(t).
Si riesce a scriverla in modo da vedere una relazione col fenomeno dei
battimenti?
- (⋆) si consideri
la funzione t↦z(t) = Ae−iωt+ϕ.
Se ne rappresenti il valore sul piano complesso per ogni valore di
t. Si trova
un vettore applicato nell’origine, ruotante (in quale verso?) al crescere del tempo
t. Si riesce ad
interpretare z(t) + z̄(t)
facendo intervenire il moto armonico?
Capitolo 8
Equazioni differenziali
Ebbi dunque il mio relatore, tanto coscienzioso quanto
ben disposto; si lasciò sfuggire qualche lacuna nelle
dimostrazioni, però mi diede utili consigli sulle virgole.
André Weil, Ricordi di apprendistato, vita di un matematico
In questo capitolo studiamo tre tipi di equazioni differenziali, ossia equazioni in cui
l’incognita è una funzione, e che coinvolgono, insieme alla funzione incognita,
anche le sue derivate.
ATTENZIONE
Nello studio delle equazioni differenziali è cruciale questo risultato,
provato al Teorema 195: ogni funzione continua su un intervallo
ammette primitive.
8.1 Introduzione
Le equazioni differenziali sono un argomento importantissimo in tutte le
applicazioni della matematica, e molto vasto. Noi ci limitiamo a studiare le
equazioni differenziali di tre classi particolari, che ora descriviamo. Diciamo
però prima di tutto che, a differenza delle equazioni studiate fino ad ora,
l’incognita da determinare quando si “risolve” un’equazione differenziale
è una funzione derivabile. Le applicazioni fisiche richiedono che tale
funzione sia definita su un intervallo. Le equazioni differenziali che
studieremo hanno infinite soluzioni. Le applicazioni alla fisica richiedono di
identificare tra tutte le soluzioni una (o più) che soddisfano certe condizioni
accessorie. Noi ci limiteremo a considerare delle condizioni accessorie dette
condizioni iniziali o anche condizioni di Cauchy Vedremo che la soluzione che
verifica queste condizioni è unica se valgono opportune ipotesi usualmente
soddisfatte nelle applicazioni. Descriviamo ora le equazioni differenziali che
studieremo.
Equazioni a variabili separabili. Le equazioni a variabili separabili sono equazioni
differenziali del primo ordine ossia equazioni in cui compare, insieme alla funzione
incognita x(t),
anche la sua derivata prima (ma non compaiono derivate successive). Eventualmente
dopo opportune manipolazioni, le equazioni a variabili separabili si riconducono alla
forma seguente: |
x′(t) = f(x(t))g(t).
| (8.1) |
La proprietà essenziale è che la funzione
f non dipende
esplicitamente da t
mentre la funzione g non
dipende da x. Per esempio,
l’equazione differenziale x′ = sin tx(t)
NON è un’equazione a variabili separabili.
Definizione 162 Una funzione x(t)
si chiama soluzione dell’Eq (8.1) se ha le seguenti proprietà:
- è definita su un intervallo apero (a,b)
(limitato o meno);
- è di classe C1(a,b);
- sostituita nei due membri di (8.1) verifica l’uguaglianza per ogni
t ∈ (a,b).
Osservazione 163 (IMPORTANTE)
- Come si è detto, la funzione x(t)
da determinare deve essere definita su un intervallo. Un’equazione a
variabili separabili (con f(x)
e g(t)
continue) ammette infinite soluzioni. E’ importante notare che soluzioni
diverse della medesima equazione differenziale possono essere
definite su intervalli diversi.
- la variabile indipendente è stata indicata con la lettera t
perché in pratica indica il tempo. Però la stessa equazione differenziale
potrebbe essere scritta con lettere diverse, per esempio
y′(x) = f(y(x))g(x).
In questo caso la variabile “tempo” si è indicata con la lettera
x.
- La forma (8.1) in cui abbiamo scritto l’equazione differenziale è
corretta, ma generalmente non usata. Di regola non si indica la
dipendenza della soluzione dalla variabile “tempo” e la (8.1) si scrive
usualmente in forma
x′ = f(x)g(t).
E’ importante tener conto di ciò per esempio quando si vuol calcolare la
derivata seconda di x,
che va calcolata usando la regola di derivazione della funzione composta:
|
x″(t) = g′(t)f(x(t)) + g(t)f′(x(t))x′(t) =
= g′(t)f(x(t)) + g2(t)f′(x(t))f(x(t)).
|
- La funzione g(t)
potrebbe essere costante. In questo caso, inglobando la costante nella funzione
f(x),
l’equazione differenziale prende forma
x′ = f(x)
e si chiama autonoma o tempo invariante
Il problema di Cauchy per la (8.1) consiste nel trovare la soluzione o le soluzioni che verificano la
condizione accessoria x(t0) = x0
ove t0
ed x0
sono assegnati. Ossia si chiede di determinare una soluzione il cui grafico contiene il
punto (t0,x0).
Convenzionalmente, t0
si chiama istante iniziale e il problema di Cauchy si chiama anche
problema ai dati iniziali Il problema di Cauchy per la (8.1) si scrive
x′ = f(x)g(t)
x(t0) = x0;
Vedremo che se f(x)
è una funzione di classe C1
mentre g(t)
è continua, il problema di Cauchy ammette
soluzione unica, definita in un intorno di
t0.
Equazioni differenziali lineari del primo ordine. Le equazioni differenziali
lineari del primo ordine sono sono le equazioni
x′(t) = a(t)x(t) + f(t)
usualmente scritte
La funzione a(t)
si chiama il coeffciente dell’equazione differenziale (lineare del primo ordine) mentre
f(t) si chiama il termine noto
Assumeremo che a(t)
ed f(t) siano
continue.
L’equazione differenziale del primo ordine si dice a coeffciente costante quando
a(t) è costante e si chiama
omogenea quando f(t) = 0.
Quando f(t)≠0
l’equazione si dice completa o anche affne Data l’equazione affne (8.2), la sua
equazione omogenea associata è
x′ = a(t)x.
Notiamo che un’equazione differenziale lineare omogenea del primo ordine
x′ = a(t)x
è anche un’equazione differenziale a variabili separabili. Per definizione,
x(t)
è una soluzione dell’equazione differenziale (8.2) se è di classe
C1 su un
intervallo (a,b)
e se, sostituita nell’equazione, verifica l’uguaglianza per ogni
t ∈ (a,b). Il
problema di Cauchy per la (8.2) consiste nel cercare la soluzione che soddisfa la condizione accessoria
x(t0) = x0, ossia il cui grafico
contiene il punto (t0,x0).
Esso si scrive
x′ = a(t)x + f(t)
x(t0) = x0.
Vedremo che nel caso delle equazioni lineari
con coefficienti e termini noti continui su
ℝ,
il problema di Cauchy ammette una ed una sola
soluzione. Questa affermazione è analoga a quella fatta per
le equazioni differenziali a variabili separabili, ma c’è una
differenza importante: Nel caso delle equazioni differenziali
lineari, le soluzioni del problema di Cauchy sono definite su
ℝ.
Nel caso delle equazioni a variabili separabili in
generale il dominio è un intervallo (diverso da
ℝ)
anche se il membro destro è definito per ogni
x
e per ogni t.
Equazioni differenziali lineari del secondo ordine. Sono le equazioni di
forma |
x″ + bx′ + cx = f(t).
| (8.3) |
In quest’equazione, f(t) si chiama
il termine noto o forzante e b,
c si
chiamano i coefficienti. Noi studieremo solamente le equazioni differenziali lineari
del secondo ordine a coefficienti costati, mentre il termine noto potrà essere
costante o meno. Ancora, l’equazione si dice omogenea se il termine noto è nullo; si
dice affne o completa altrimenti; e l’equazione lineare omogenea del secondo ordine
associata alla ( 8.3) è
x″ + bx′ + cx = 0.
Per definizione, x(t)
è una soluzione dell’equazione differenziale (8.3) se è di classe
C1 su un
intervallo (a,b)
e se, sostituita nell’equazione, verifica l’uguaglianza per ogni
t ∈ (a,b). Nel
caso delle equazioni differenziali del secondo ordine, il problema di Cauchy consiste
nel risolvere
x″ + bx′ + cx = f(t),
x(t0) = x0,x′(t
0) = x1.
Ossia, si richiede una soluzione che in un istante
t0 ha il
valore x0
e anche tale che la sua derivata nel medesimo istante
t0 vale
x1.
Geometricamente, si cerca una soluzione il cui grafico passa per il punto
(t0,x0) e che, in tale punto ha
tangente di pendenza x1.
Convenzionalmente, l’istante t0
si chiama ancora istante iniziale Ricordando l’interpretazione della derivata come
velocità istantanea, il problema di Cauchy consiste nel trovare una traiettoria
t↦x(t) che ad un certo
istante t0 passa
per la posizione x0
con velocità x1.
Anche nel caso delle equazioni differenziali lineari
del secondo ordine, con termine noto definito su
ℝ,
le soluzioni sono definite su ℝ.
Osservazione 164 Consideriamo il problema
x″ + bx′ + cx = f(t),x(t
0) = x0
Questo non è un problema di Cauchy perché non impone alcuna
condizione alla velocità iniziale, ed ammette infinite soluzioni: una soluzione
per ciascuna condizione che si ottiene assegnando anche il valore di x′(0).
Analogamente, il problema x″ + bx′ + cx = f(t),
x′(t
0) = x1
non è un problema di Cauchy. ■
8.2 Soluzione delle quazioni differenziali a variabili separabili
Ricordiamo che queste sono le equazioni della forma |
x′ = f(x)g(t)ossiax′(t) = f(x(t))g(t).
| (8.4) |
Le funzioni f(x)
e g(t)
sono continue (più avanti richiederemo la derivabilità di
f(x)).
Studiamo prima come trovare tutte le soluzioni dell’equazione, e poi come trovare le
soluzioni del problema di Cauchy |
x′ = f(x)g(t),x(t
0) = x0.
| (8.5) |
Il primo passo nella ricerca delle soluzioni consiste nel ricercare le
eventuali soluzioni costanti. Un’equazione a variabili separabili
può ammettere o meno soluzioni costanti. Naturalmente, se
f(x) ≡ 0 oppure
g(t) ≡ 0
l’equazione si riduce a
x′ = 0
e le sue soluzioni sono tutte e sole le funzioni costanti. Le funzioni definite su un
intervallo e costanti, sono tutte e sole quelle con derivata nulla. Dunque, le soluzioni
x(t) ≡ k che
risolvono la (8.4) sono quelle per cui vale
0 = f(k)g(t)per ogni t.
Ciò accade se il numero k
è uno zero della funzione f(x).
Si ha quindi:
Primo passo della ricerca di soluzioni: si risolve l’equazione
f(x) = 0.
Se il numero
k
risolve quest’equazione, allora la funzione costante
x(t) = k
è soluzione di ( 8.5).
Ora ricerchiamo soluzioni non costanti. Se
f(x(t))≠0 per un
valore t = t0,
la disuguaglianza continua a valere in un intorno di
t0, grazie
al teorema di permanenza del segno per le funzioni continue. Dunque, in un intorno
di t0 si
può scrivere |
1
f(x(t))x′(t) = g(t).
| (8.6) |
Le due funzioni
g(t),h(x) = 1
f(x)
sono continue. Dunque ammettono primitive
G(t) ed
H(x).
Ricordando la formula per la derivata delle funzioni composte, si vede che la (8.6)
è niente altro che
d
dtH(x(t)) = g(t) = d
dtG(t).
Abbiamo cosìdue funzioni della variabile
t,
definite sul medesimo intervallo e con la medesima derivata. Dunque, la
differenza di queste due funzioni è costante: |
H(x(t)) = G(t) + c.
| (8.7) |
Quest’espressione si chiama integrale primo o integrale generale dell’equazione a
variabili separabili. Ogni soluzione non costante dell’equazione si trova assegnando
a c
un opportuno valore. E’ anche possibile che certi valori di
c
portino ad identificare soluzioni costanti, ma ciò non è garantito
perché il procedimento che abbiamo fatto (in particolare la divisione per
f(x(t)) ) non è
lecito se x(t)
è una soluzione costante.
8.2.1 Problema di Cauchy per le equazioni differenziali a variabili
separate
Consideriamo ora il problema di Cauchy (8.5) e ricerchiamo condizioni perché
esso ammetta soluzioni, e perchè la soluzione sia unica. Vale il seguente
Teorema 165 (Teorema di Cauchy) Se la funzione g(t)
è continua in un intorno di t0
e se la funzione f(x)
è continua in un intorno di x0,
il problema di Cauchy (8.5) ammette soluzione, definita in un opportuno
intorno di t0.
Se inoltre f(x)
è di classe C1,
la soluzione è unica.
Per trovare esplicitamente la soluzione, dobbiamo prima di tutto
controllare se la soluzione richiesta è costante, cosa che accade se
f(x0) = 0. Altrimenti,
dobbiamo sostituire t0
ed x0
nei due membri di (8.7). Ciò identifica il valore della costante
c.
Ossia, si deve scegliere
c0 = H(x(t0)) − G(t0).
Ciò fatto, per ogni t
si risolve rispetto ad x
l’equazione
H(x(t)) = G(t) + c0.
Osservazione 166 Se f(x0)≠0,
la funzione continua f(x)
ha segno costante in un intorno di x0
cosìche H(x)
è ivi continua e strettamente monotona. Infatti, la sua derivata
H′(x) = 1∕f(x)
ha segno costante. Dunque l’immagine di H(x)
è un intervallo I
che contiene G(t0) + c.
Per t
“vicino” a t0,
avremo G(t) + c ∈ I,
perché anche G(t)
è continua Essendo strettamente monotona, H(x)
è invertibile. L’unica soluzione x(t)
del problema (8.7), e quindi del problema di Cauchy, è data da
x(t) = H−1 G(t) + c
0
ed è definita per ogni t
in un opportuno intorno di t0.
Però non è detto che sia sempre possibile esprimere questa funzione
mediante funzioni elementari. Spesso dovremo contentarci dell’espressione
implicita (8.7) e della determinazione del valore c0. ■
Il significato geometrico del teorema 165 va capito bene: esso asserisce che, se
g(t) è continua
ed f(x) è
derivabile, i grafici di soluzioni diverse della medesima equazione differenziale non
si intersecano. La figura 8.1 mostra, in azzurro, i grafici di alcune soluzioni
dell’equazione differenziale
Il grafico in rosso interseca le soluzioni dell’equazione differenziale e quindi
non è grafico di una soluzione di (8.8).
Osservazione 167 Si sa, dalla tavola delle derivate fondamentali, che
d
dtet = et, d
dteat = aeat.
Quindi, la funzione
ceat
risolve il problema di Cauchy
x′ = ax,x(0) = c.
Il Teorema 165 garantisce che non ci sono altre funzioni che verificano queste
condizioni. Infatti, il secondo membro f(x) = ax
è funzione derivabile di x. ■
Vediamo ora un’applicazione del Teorema 165, che conduce a risolvere un’equazione
differenziale lineare omogenea del primo ordine.
Esempio 168 Sia
a(t)
una funzione continua e consideriamo l’equazione differenziale
x′ = a(t)x.
Vogliamo trovarne tutte le soluzioni. Come sempre quando si studiano
equazioni a variabili separabili, se ne cercano prima di tutto le soluzioni
costanti. In questo caso l’unica soluzione costante è x(t) ≡ 0.
Se x(t)
è una soluzione non costante, essa rimane o sempre positiva o
sempre negativa. Infatti, essendo continua e definita su un intervallo, se
cambiasse segno dovrebbe annullarsi in un certo istante t0
e quindi x(t)
sarebbe una soluzione non costante del problema di Cauchy
x′ = a(t)x,x(t
0) = 0.
Cioè, questo problema avrebbe sia la soluzione non costante
x(t)
che la soluzione identicamente nulla. Il Teorema 165 mostra che ciò non può
essere, e quindi che
x(t)
non si annulla: o prende valori solamente positivi
oppure prende valori solamente negativi. Dunque, possiamo dividere per
x(t)
ottenendo
a(t) = x′(t)
x(t) = d
dt log |x(t)|.
Sia ora A(t)
una primitiva di a(t).
Allora vale
log |x(t)| = A(t) + c ossia|x(t)| = eceA(t).
Il numero
c
è qualsiasi e quindi il numero
k = ec
è un numero positivo qualsiasi:
|x(t)| = keA(t),k > 0.
Ma, x(t)
ha segno costante, e quindi abbiamo
per ogni t vale x(t) = |x(t)| oppure x(t) = −|x(t)|.
Dunque avremo
x(t) = +keA(t) oppurex(t) = −keA(t).
In definitiva,
x(t) = keA(t)
con k = ±ec
reale qualsiasi, non nullo. Si noti che la soluzione
x(t) ≡ 0 non si è ritrovata.
Però, noi sappiamo che x(t) ≡ 0
è una soluzione dell’equazione e quindi possiamo permettere a
k di prendere
il valore 0,
trovando |
x(t) = keA(t)k reale qualsiasi
| (8.9) |
come espressione di tutte le soluzioni. ■
Si noti il ruolo particolare delle soluzioni costanti: talvolta queste non si ritrovano
nell’integrale generale. Può essere possibile farvele comparire forzando la
costante ad assume dei valori che non potrebbe assumere. Talvolta invece ciò
non può farsi. Per questa ragione, le soluzioni costanti si chiamano anche
soluzioni singolari Un’altra applicazione importante del Teorema 165 è che
spesso permette di tracciare qualitativamente il grafico delle soluzioni,
senza risolvere l’equazione differenziale, come mostra l’esempio seguente:
Esempio 169 Consideriamo l’equazione differenziale
y′ = (1 − x2) sin y
Il Teorema 165 permette immediatamente di concludere che le soluzioni sono
tutte funzioni limitate. Infatti, quest’equazione ha infinite soluzioni costanti,
che “affettano” il piano in strisce parallele:
y(x) = kπ,k ∈ ℤ.
Ovviamente queste soluzioni sono limitate. Sia
y(x)
un’altra soluzione. Il punto
(x0,y(x0))
del suo grafico starà in una striscia
{(x,y),x ∈ ℝ,kπ < y < (k + 1)π}.
Il grafico della soluzione non può uscire da questa striscia altrimenti, per
il teorema dei valori intermedi, dovrebbe intersecare il grafico di una delle
soluzioni costanti; e ciò non può essere per il Teorema 165. In realtà può
dirsi anche di più: consideriamo una soluzione il cui grafico sta nella striscia
0 < y < π
(le altre strisce si trattano in modo analogo). In questa striscia,
sin y > 0
e quindi avremo
y′(x) > 0se e solo se (−1 < x < 1).
Dunque, una soluzione y(x)
(il cui grafico è in questa striscia) decresce per x < −1
e per x > 1.
In particolare, x = −1
è punto di minimo ed x = +1
è punto di massimo delle soluzioni. Note queste informazioni, non è diffcile
disegnare qualitativamente il grafico della soluzione. I grafici di alcune soluzioni
sono in figure 8.2. ■
Infine, consideriamo l’esempio seguente, che mostra che il problema di
Cauchy (8.5) in generale ha più soluzioni, ovviamente quando la funzione
f(x) non è
di classe C1:
Esempio 170 Si consideri il problema di Cauchy
x′ = x3,x(1) = 0.
Ovviamente,
x(t) = 0
risolve questo problema. Si verifichi che anche la funzione
x(t) = 2
3(t − 1) 3∕2 set ≥ 1
0 set < 1
risolve il medesimo problema di Cauchy. ■
8.2.2 Domini massimali di soluzione
Per definizione, il dominio di una soluzione di un’equazione differenziale deve essere
un intervallo (limitato o meno). Può venire il dubbio che nel caso in cui il membro
destro di un’equazione a variabili separabili sia regolare il dominio debba essere
ℝ. E’
importante sapere che ciò è falso.
Esempio 171 Consideriamo il problema di Cauchy
x′ = 1 + x2,x(t
0) = x0.
Ricordando che
d
dt tan(t + c) = 1 + tan 2(t + c)
si vede immediatamente che la soluzione di questo problema di Cauchy è
x(t) = tan (t − t0) + arctan x0
definita sull’intervallo
t0 −π
2 − arctan x0 < t < t0 + π
2 − arctan x0.
La soluzione ha per dominio un intervallo limitato, nonostante il fatto che il
secondo membro dell’equazione non dipenda esplicitamente da t,
e sia una funzione di classe C∞.
Il dominio della soluzione cambia al variare di t0,
e questo è ovvio; ma, fissato il valore di t0,
cambia anche al variare di x0. ■
Naturalmente, una soluzione definita su un intervallo
(a,b) è anche soluzione su
qualsiasi sottointervallo (c,d) ⊆ (a,b).
L’interesse di quest’osservazione si vede leggendola al
contrario: può essere che si riesca ad identificare un intervallo
(c,d) su cui
la soluzione è definita, ma che questo non sia il massimo intervallo su cui la
soluzione è definita. Tale massimo intervallo si chiama dominio massimale
della soluzione. E’ molto facile verificare se un intervallo su cui abbiamo
trovato una soluzione è dominio massimale o meno. Torniamo a considerare
le soluzioni dell’equazione dell’Esempio 171. Queste divergono per
x
tendente agli estremi dell’intervallo su cui sono definite. Ciò avviene sempre:
Teorema 172 Si consideri l’equazione differenziale
x′ = g(t)f(x).
Supponiamo che g(t)
sia continua su ℝ
e che f(x)
sia derivabile (e quindi continua) su ℝ.
Consideriamo la soluzione che verifica
x(t0) = x0.
Sia (S,T)
il dominio massimale della soluzione e sia T < +∞.
Allora,
lim t→T−|x(t)| = +∞.
Proprietà analoga vale per t → S+
se S > −∞.
Di conseguenza:
- se troviamo una soluzione definita su (a,b)
con −∞ < a < b < +∞
e che non diverge per t
tendente ad uno dei due estremi dell’intervallo, questo intervallo non è
il dominio massimale della soluzione;
- le soluzioni dell’equazione differenziale dell’Esempio 169, essendo limitate,
sono definite su ℝ.
Una soluzione definita su ℝ può
avere limite o meno per t → +∞
oppure per t →−∞.
Per tracciare qualitativamente il grafico di soluzioni di equazioni differenziali, è
utile conoscere il risultato seguente:
Teorema 173 Sia
f(x)
una funzione di classe
C1(ℝ)
e consideriamo un’equazione differenziale del primo ordine autonoma
x′ = f(x).
Sia
x(t)
una sua soluzione definita su una semiretta. Se
lim t→+∞x(t) = l ∈ ℝ(oppure lim t→−∞x(t) = l ∈ ℝ).
Allora,
f(l) = 0.
Ossia, le soluzioni di equazioni differenziali autonome del primo
ordine, con secondo membro regolare, se ammettono limite per
x → +∞ oppure
x →−∞,
convergono al valore di una soluzione costante.
8.3 Le equazioni differenziali lineari
La seconda classe di equazioni che vogliamo trattare è quella delle equazioni
differenziali lineari, limitandoci ai casi:
- equazioni differenziali lineari del primo ordine
x′ = a(t)x + f(t)
col coeffciente a(t)
e termine noto f(t)
funzioni anche non costanti (assumeremo continue, ma basta che siano
dotate di primitiva anche in senso generalizzato);
- equazioni differenziali lineari del secondo ordine a coefficienti costanti
x″ + bx′ + cx = f(t)
con b
e c
costanti (mentre f(t)
non è costante; assumeremo per semplicità che sia continua, ma basta
che sia dotata di primitiva anche in senso generalizzato). Il metodo che
vedremo per le equazioni del secondo ordine si applica anche ad equazioni
differenziali lineari di ordine più alto, purché a coefficienti costanti:
x(n) + a
1x(n−1) + ⋅ + a
n−1x′ + a
nx = f(t).
8.3.1 Equazioni differenziali lineari del primo ordine
Studiamo l’equazione |
x′ = a(t)x + f(t).
| (8.10) |
Ricordiamo che quest’equazione si dice completa o affne se
f(t)≠0 e che
l’equazione differenziale lineare omogenea ad essa associata è quella che si ottiene
ponendo f(t) = 0,
ossia è
Questa è un’equazione a variabili separabili e si è già risolta all’Esempio 168.
Ogni sua soluzione ha forma
x(t) = keA(t)
ove A(t) è una qualsiasi
primitiva di a(t). Se vogliamo
la soluzione che verifica x(t0) = x0
sceglieremo
k = e−A(t0)x
0e quindix(t) = eA(t)−A(t0)x
0.
Nel caso particolare in cui a(t) ≡ a è
costante, una delle primitive è at
e quindi le soluzioni sono
x(t) = keat
Risolviamo ora l’equazione completa. Presentiamo i calcoli nel caso in cui
a(t) ≡ a è
costante. In modo del tutto analogo troveremo la soluzione anche nel caso del
coeffciente variabile. Prima di tutto scriviamo la (8.10) come
x′− ax = f(t).
Poi moltiplichiamo i due membri per e−at:
e−atx′− ae−atx = e−atf(t).
L’espressione a sinistra è la derivata di un prodotto e quindi si ha:
d
dte−atx(t) = e−atf(t).
Dunque, una primitiva del membro destro e una del membro sinistro differiscono
per una costante (ricordiamo che stiamo lavorando su un intervallo):
e−atx(t) = k + ∫
cte−asf(s)ds
ossia
x(t) = eatk + eat ∫
cte−asf(s)ds
ove k è un qualsiasi
numero reale. Quando a = a(t)
calcoli del tutto analoghi portanto a trovare la formula seguente per la soluzione. In questa formula,
A(t) è una qualsiasi
primitiva di a(t): |
x(t) = eA(t)k + eA(t) ∫
ct e−A(s)f(s) ds.
| (8.12) |
Osserviamo ora questa formula, notando in particolare due fatti importanti.
La formula (8.12) mostra che x(t)
è somma di due addendi. Il primo è
eA(t)k.
Al variare della costante arbitraria k
quest’addendo dà tutte le soluzioni dell’equazione differenziale lineare
omogenea associata. Il secondo è |
eA(t) ∫
ct e−A(s)f(s) ds.
| (8.13) |
Questa è una particolare soluzione dell’equazione completa (quella che si annulla
per t = c).
Dunque: l’integrale generale di (8.10) si ottiene scegliendo una soluzione particolare
dell’equazione (8.10) stessa e sommandogli tutte le soluzioni dell’omogenea
associata (8.11).
Se accade che il termine affne è combinazione lineare di due funzioni
αf(t) + βg(t)
allora
∫
cteA(s) αf(s) + βg(s) ds = α∫
cteA(s)f(s)ds + β∫
cteA(s)g(s)ds
si ricordi la proprietà di linearità del calcolo delle primitive. Dunque, quando il
termine noto è somma di funzioni più semplici, per trovare una soluzione
particolare si possono trovare soluzioni particolari corrispondenti ai singoli addendi,
e poi sommarle. Introduciamo ora i termini seguenti: il membro destro di (8.12) si
chiama integrale generale di (8.10) mentre la funzione in (8.13) si chiama
integrale particolare di (8.10). Ciò che abbiamo notato è particolarmente
importante, e vale la pena di evidenziarlo:
Per trovare l’integrale generale dell’equazione completa (8.10) si
calcola, in qualunque modo, anche semplicemente per tentativi, una
soluzione particolare dell’equazione (8.10) stessa e le si sommano tutte
le soluzioni dell’omogenea associata (8.11). Quando il termine noto è
somma di più addendi, una soluzione particolare si trova ricercando
soluzioni particolari relative ai singoli addendi, e quindi sommandole.
8.3.2 Problema di Cauchy per le equazioni differenziali lineari del primo
ordine
Ricordiamo che il problema di Cauchy per le equazioni differenziali lineari del primo
ordine è il problema |
x′ = a(t)x + f(t),x(t
0) = x0.
| (8.14) |
Supponiamo che f(t)
sia definita su ℝ.
Allora, questo problema ammette soluzione unica, definita su
ℝ. Essa
si ottiene imponendo l’uguaglianza
x(t0) = x0 ossiax0 = eA(t0)k + eA(t0) ∫
ct0
e−A(s)f(s) ds.
In particolare, se si è scelto c = t0
e come primitiva A(t)
quella che si annulla in t0,
basta scegliere k = x0.
Ciò completa quanto si può dire in generale sull’equazione differenziale lineare
del primo ordine. Però in pratica è importantissimo saper trattare col minimo di
calcoli alcuni casi particolari, che ora andiamo a vedere. Si tratta di equazioni
col coeffciente costante e termine noto di tipo particolare, che si incontra
frequentemente nelle applicazioni alla fisica.
Casi particolari di equazioni differenziali lineari del primo ordine, a coefficienti
costanti
Vogliamo dare dei metodi semplici per calcolare una soluzione particolare
dell’equazione
x′ = ax + f(t)
(con coeffciente a costante)
quando il termine noto f(t)
ha forma particolare. Esaminiamo i casi che interessano:
Il caso f(t) = 1 ed
a≠0In questo caso, si ricerchi
una soluzione di forma x(t) = c,
costante. Sostituendo nei due membri dell’equazione si vede che deve essere
0 = ac + 1ossia c = −1∕a.
Dunque, se f(t) = α,
costante, una soluzione particolare è
x(t) = −α
a.
La forma esplicita della soluzione non va ricordata, nè in questo caso
né nei successivi. Bisogna invece capire il procedimento in modo da
poterlo usare correttamente, ricavando volta per volta l’espressione
della soluzione particolare.
Il caso f(t) = t
ed a≠0Si
ricerchi una soluzione di forma
x(t) = ct + d.
Sostituendo nei due membri dell’equazione si vede che deve aversi
c = act + ad + te quindi c = −1∕a, d = −1∕a2.
Il caso f(t) polinomio
ed a≠0Procedendo
per sostituzione, come nei casi precedenti, si vede che una soluzione è un polinomio dello
stesso grado di f(t).
Il caso f(t) = 1
ed a = 0.
In questo caso l’equazione è
x′ = 1
e le sue soluzioni si ottengono semplicemente calcolando primitive,
x(t) = t + c. Conviene però
cercare di procedere come nei casi precedenti, per capire meglio il metodo. In questo caso,
x(t) = α non risolve l’equazione
completa, infatti, x(t) = α
risolve l’equazione omogenea. Sostituendo si trova infatti
0 = aα + 1 = 0 ⋅ α + 1
e l’uguaglianza non può valere. Però, se si prova a sostituire
x(t) = αt
si trova
α = 0 ⋅ (αt) + 1
e ora l’uguaglianza vale con α = 1.
Ossia in questo caso la soluzione è un polinomio, di grado
1 invece che
di grado 0.
Il caso f(t) polinomio
ed a = 0Procedendo
come sopra, si vede che una soluzione particolare è un polinomio, di grado
n + 1 se il termine
noto f(t) ha
grado n. I
coefficienti del polinomio si ricavano sostituendo nei due membri e richiedendo che i
due membri siano uguali (alternativamente ed in modo più semplice, calcolando le
primitive dei due membri).
Il caso f(t) = ebt
con b≠aIn
questo caso, una soluzione particolare ha forma
x(t) = αebt α = 1
b−a
come si vede immediatamente sostituendo nei due membri dell’equazione.
Il caso f(t) = ebt
con b = aIn
questo caso, x(t) = αebt = αeat
risolve l’equazione omogenea associata, e quindi non può risolvere l’equazione
completa. Infatti, sostituendo si trova
αaeat = aαeat + eat ossia0 = eat
uguaglianza ovviamente falsa. Una soluzione particolare però si trova
scegliendo
x(t) = teat,
come si vede immediatamente sostituendo nei due membri dell’equazione.
Il caso f(t) = p(t)ebt
con p(t)
polinomio.Vanno esaminati separatamente due casi:
-
caso a≠b:
-
una soluzione particolare dell’equazione completa è
x(t) = q(t)ebt
ove q(t)
è un polinomio dello stesso grado di p(t).
-
caso a = b:
-
una soluzione particolare dell’equazione completa è
ove q(t) è un
polinomio di grado n + 1
se n è il
grado di p(t).
I coefficienti del polinomio si ricavano sostituendo nei due membri e
richiedendo che i due membri siano uguali.
Nei casi particolari precedenti, un’attenzione
particolare è necessaria quando il temine forzante
f(t)
ha forma p(t)y(t),
con p(t)
polinomio ed y(t)
soluzione dell’equazione differenziale lineare omogenea associata (e
quindi y(t)
multiplo di eat).
In tal caso una soluzione particolare ha forma
y(t) = q(t)eat
ove q(t)
è un polinomio il cui grado supera di
1
quello di p(t).
Osservazione 174 Quest’osservazione semplifica un po’ i calcoli nel caso
a = b:
il termine costante q0
del polinomio q(t)
conduce a q0eat
che è una soluzione dell’equazione lineare omogenea associata e quindi
possiamo limitarci a lavorare con polinomi q(t)
privi di termine costante; ossia, possiamo sostituire la (8.15) con
x(t) = tq1(t)eat
con q1(t)
polinomio dello stesso grado di p(t). ■
Notiamo ciò che hanno in comune i casi particolari precedenti: il termine noto appartiene ad
un insieme 𝒮
di funzioni, che gode di questa proprietà: le derivate di elementi di
𝒮
sono ancora elementi dell’insieme; e inoltre, moltiplicando elementi di
𝒮 si trovano altri
elementi di 𝒮.
L’insieme 𝒮 = {α sin ωt}
con α ∈ ℝ,
ω ∈ ℝ
non ha questa proprietà di invarianza, perché la derivata di
sin ωt è
ω cos ωt. Però,
l’insieme 𝒮 = {α sin ωt + β cos ωt}
(con α
e β
reali qualsiasi) gode della proprietà detta sopra. E quindi:
Il caso f(t) = sin ωtIn
questo caso una soluzione particolare è
x(t) = α sin ωt + β cos ωt
come si vede sostituendo nell’equazione: per avere una soluzione, l’uguaglianza seguente deve
valere per ogni t:
αω cos ωt − βω sin ωt = aα sin ωt + aβ cos ωt + sin ωt.
Ciò accade se
αω = aβ − βω = aα + 1 ossia α = − a
ω2+a2
β = − ω
ω2+a2.
In modo analogo si tratta il caso f(t) = cos ωt
ed i casi in cui il termine noto è combinazione lineare di polinomi moltiplicati per
seni e coseni.
8.3.3 L’equazione differenziale lineare del secondo ordine
Premettiamo un’osservazione importante sull’equazione differenziale lineare
omogenea del primo ordine, a coeffciente costante:
Si è già notato che le soluzioni dell’equazione
x′ = ax
sono tutte e sole le funzioni x(t) = keat.
Qui, a
è costante. L’osservazione che ci interessa è che sia
a
che la costante k
possono essere sia reali che complessi, si veda il paragrafo 7.6.
Consideriamo ora le soluzioni di
x′ = ax + bect
con a,
b
e c
numeri complessi ed a diverso da c.
Un calcolo analogo a quello fatto nel caso reale mostra che le soluzioni
sono le funzioni
keat + γect
(sostituendo nell’equazione si trova
γ = b∕(c − a)).
Passiamo ora a capire come sia possibile risolvere equazioni lineari del secondo
ordine, a coefficienti costanti, omogenee o meno. Per questo indichiamo con
D
l’operazione di fare la derivata e consideriamo un’equazione data in questa forma |
(D − m1)(D − m2)x = f(t).
| (8.16) |
Spieghiamo cosa si intende con questa notazione. Con
(D − m2)x
intendiamo
(D − m2)x(t) = Dx(t) − m2x(t) = x′(t) − m
2x(t)
A quest’espressione applichiamo D − m1,
ossia |
(D − m1) (D − m2)x = (D − m1) x′(t) − m
2x(t)
= D x′(t) − m
2x(t) − m1 x′(t) − m
2x(t)
= x″(t) − m2x′(t) −m
1x′(t) − m
1m2x(t) .
|
Dunque, la (8.16) è niente altro che l’equazione di secondo ordine |
x″ − (m1 + m2)x′ + m
1m2x = f.
| (8.17) |
Come risolvere la (8.16) è immediatamente evidente. Si introduca il simbolo
y(t) per
indicare la funzione (ancora incognita)
y(t) = (D − m1)x(t).
Allora, la funzione y(t)
deve risolvere l’equazione differenziale
equazione che sappiamo risolvere. Calcolata
y(t), la
soluzione x(t)
di (8.16) si ottiene semplicemente risolvendo
Questi sono calcoli che già sappiamo fare, con
m1,
m2 sia
reali che complessi. Ma ora, se l’equazione da risolvere è data nella forma |
x″ + bx′ + cx = f(t),
| (8.20) |
si sa come ridurla alla forma (8.16): si risolve l’equazione
ottenendo le due soluzioni m1
ed m2,
che saranno numeri reali oppure complessi. Si sa che queste soluzioni verificano
m1 + m2 = −b,m1m2 = c
e quindi la (8.20) è niente altro che la (8.16), con questi numeri
m1 ed
m2; e
quindi si sa come risolvere tutte le equazioni differenziali lineari a coefficienti
costanti, del secondo ordine. In questo contesto, l’equazione (8.21) si chiama
l’equazione caratteristica dell’equazione differenziale e le sue soluzioni si chiamano
autovalori dell’equazione differenziale.
Si ricordi che se i coefficienti
b
e
c
sono reali, gli autovalori possono essere sia reali che complessi, coniugati
l’uno dell’altro.
Osservazione 175 Si parla di “equazione caratteristica” ed “autovalore”
anche nel caso delle equazioni lineari del primo ordine. Nel caso di x′ = ax,
l’equazione caratteristica è λ − a = 0
e l’unico autovalore è a.
In particolare, è reale se il coeffciente è reale. ■
E’ del tutto ovvio che un metodo di fattorizzazione analogo si possa applicare a tutte le
equazioni differenziali lineari a coefficienti costanti, di qualsiasi ordine.
A noi non interessa scrivere esplicitamente una formula per le soluzioni
dell’equazione (8.20). La (8.20) in generale si risolve risolvendo prima la (8.18) e
poi la (8.19). Interessa piuttosto conoscere il risultato seguente, che è
semplice conseguenza dei fatti 1–3 studiati per le equazioni del primo ordine:
Oltre a questo fatto, interessa:
- saper risolvere con prontezza i casi particolari che si incontrano più
frequentemente nelle applicazioni;
- saper trovare soluzioni reali nel caso in cui gli autovalori siano numeri
complessi e coniugati.
Casi particolari di equazioni differenziali lineari del secondo ordine,
omogenee
Esaminiamo i seguenti casi, che si risolvono applicando i metodi visti per le
equazioni lineari del primo ordine con termine noto di tipo particolare.
Caso 1: autovalori reali e distinti. In questo caso, risolvendo una dopo
l’altra le due equazioni del primo ordine (8.18) e (8.19), si vede che l’integrale
generale dell’equazione è
αem1t + βem2t
con α e
β
arbitrari numeri reali.
Caso 2: autovalori coincidenti. Sia
m = m1 = m2 il
valore comune degli autovalori In questo caso, risolvendo una dopo l’altra le due
equazioni del primo ordine (8.18) e (8.19), si vede che l’integrale generale
dell’equazione è
αemt + βtemt
con α e
β
arbitrari numeri reali. Si noti il caso particolare in cui
m1 = m2 = 0. In
questo caso la soluzione generale è
α + βt.
Caso 3: autovalori complessi e coniugati. In questo caso gli autovalori
sono distinti e quindi, risolvendo una dopo l’altra le due equazioni del primo
ordine (8.18) e (8.19), si vede che l’integrale generale dell’equazione è |
x(t) = αem1t + βem2t
| (8.22) |
con α e
β
arbitrari numeri che ora potranno essere o reali o complessi. Nella maggior
parte delle applicazioni i coefficienti dell’equazione sono reali e quindi
m1 ed
m2 sono
tra loro coniugati
m1 = ξ + iω,m2 = ξ − iω.
In tal caso, la (8.22) prende forma
x(t) = eξt αeiωt + βe−iωt .
Se α e
β sono
numeri complessi qualsiasi, queste soluzioni prendono valori complessi.
Spesso interessa identificare quelle che prendono valori reali. Dato che
eiωt ed
e−iωt
sono tra loro coniugate, ciò si ottiene scegliendo anche
α e
β tra
loro coniugati:
α = c + id,β = c − id.
Con questa scelta si trova
x(t) = eξt 2ℜe (c + id)eiωt = 2eξt c cos ωt − d sin ωt.
Nei corsi di fisica si preferisce scrivere quest’espressione in una forma diversa.
Prima di tutto questa si scrive
eξtc2 + d2 c
c2 + d2 cos ωt − d
c2 + d2 sin ωt.
I numeri
c
c2 + d2, d
c2 + d2
sono le coordinate di un punto della circonferenza trigonometrica e quindi esiste un
angolo ϕ
tale che
c
c2 + d2 = cos ϕ, d
c2 + d2 = sin ϕ.
Dunque, |
x(t) = Aeξt (cos ϕ) cos ωt − (sin ϕ) sin ωt = Aeξt cos(ωt + ϕ).
| (8.23) |
In quest’espressione, A
è un numero non negativo arbitrario. Anche
ϕ
è un numero arbitrario ma naturalmente basta scegliere
ϕ ∈ [0, 2π). Quando
la soluzione x(t)
è scritta in forma (8.23), si usa la seguente terminologia:
- il numero A
si chiama ampiezza
- il numero ϕ
si chiama fase
- il numero ω
si chiama frequenza angolare
- il numero −ξ
(notare il segno!) si chiama costante di tempo del sistema.
Casi particolari di equazioni differenziali lineari del secondo ordine complete
Nel caso affne, le soluzioni si trovano risolvendo a catena le due equazioni
differenziali del primo ordine (8.18) e (8.19), con calcoli che sappiamo già fare.
Consideriamo esplicitamente i casi in cui il termine noto ha forma particolare, e
ricerchiamo soluzioni particolari dell’equazione. A queste, per ottenere la
soluzione generale, dovremo aggiungere tutte le soluzioni dell’equazione differenziale
lineare omogenea associata. ossia
SOMIGLIANZA col caso del primo ordine: ricercheremo soluzioni particolari di forma
p(t)eγt, con
p(t) polinomio
di grado n,
se γ
non è autovalore dell’equazione; altrimenti ricercheremo soluzioni di forma
tp(t)eγt se
γ è autovalore
semplice oppure t2p(t)eγt se
γ è autovalore doppio.
In ambedue i casi, p(t)
ha grado n
(si veda l’Osservazione 174 per spiegare l’assenza del termine di grado
0
e, nel caso dell’autovalore doppio, anche di grado
1).
DIffERENZA rispetto al caso del primo ordine: il procedimento
per la ricerca della soluzione particolare ora va fatto due volte, una per
l’equazione (8.18) e una seconda volta per (8.19). Ciò spiega perché è possibile
che il grado debba essere aumentato di due unità invece che di una.
- il caso f(t) = p(t)eξt sin ωt
oppure f(t) = p(t)eξt cos ωt
con p(t)
polinomio di grado n.
Nel caso delle equazioni del primo ordine (a coefficienti reali)
ξ + iω non
è mai un autovalore dell’equazione e quindi queste funzioni non sono mai
soluzioni dell’equazione; e quindi si ricerca una soluzione particolare in forma |
q1(t)eξt sin ωt + q
2(t)eξt cos ωt
| (8.24) |
con q1(t) e
q2(t) polinomi ancora
di grado n.
SOMIGLIANZA col caso del primo ordine: anche nel caso dell’equazione
lineare del secondo ordine si ricerca una soluzione di questa stessa forma (8.24) se
ξ + iω non è autovalore
dell’equazione;
DIffERENZA rispetto al caso del primo ordine: nel caso del secondo ordine, il numero
complesso ξ + iω
può essere autovalore dell’equazione (necessariamente semplice se i
coefficienti sono reali). In questo caso, dovremo aumentare il grado di
1,
ricercando una soluzione particolare di forma
eξt tq
1(t) sin ωt + tq2(t) cos ωt
con q1(t) e
q2(t) polinomi del
medesimo grado di p(t).
Quando il termine forzante ha forma
p(t)eξt sin ωt
oppure p(t)eξt cos ωt,
con ξ + iω
autovalore dell’equazione, si dice che si presenta il fenomeno della
risonanza e si dice che il termine forzante è risonante
8.3.4 Problema di Cauchy per le equazioni differenziali lineari del secondo
ordine
Ricapitolando, nel caso di un generico termine noto
f(t) (e non solo
quando f(t)
ha forma particolare) l’integrale generale di (8.17) è
x(t) = αu1(t) + βu2(t) + F(t)
con F(t)
integrale particolare dell’equazione completa ed
u1(t),
u2(t)
integrali particolari dell’equazione omogenea associata (questi avranno forme
diverse a seconda che gli autovalori siano reali o meno, coincidenti o meno). Il
problema di Cauchy per l’equazione del secondo ordine (8.17) consiste nel
determinarne una soluzione che soddisfa alle ulteriori condizioni di Cauchy
x(t0) = x0,x′(t
0) = x1.
Non è diffcile mostrare
Teorema 176 Sia f(t)
continua su ℝ.
Il problema di Cauchy ammette soluzione unica qualunque siano t0,
x0
ed x1
e questa soluzione è definita su ℝ.
8.3.5 Il comportamento in futuro e la stabilità
Le applicazioni alla fisica delle equazioni differenziali, lineari o meno, richiedono spesso
di poter dedurre informazioni sul comportamento delle soluzioni in futuro, ossia
per t → +∞,
senza dover preventivamente risolvere l’equazione.
Noi ci limitiamo a considerare questo problema per le soluzioni dei problemi
di Cauchy |
x′ = ax,x(t
0) = x0.
| (8.25) |
|
x″ + bx′ + cx = 0,x(t
0) = x0,x′(t
0) = x1,
| (8.26) |
con coefficienti reali e costanti. Si noti: abbiamo esplicitamente assunto
che il termine affne sia nullo.
Diamo quindi alcune definizioni in forma semplificata, valida solamente
per le equazioni differenziali (8.25) e (8.26).
Ripetiamo che se l’equazione da studiare non fosse lineare a coefficienti costanti, queste
definizioni andrebbero precisate meglio. Le soluzioni della (8.25) sono le
funzioni
x(t) = eatx
0.
Dunque, ricordando che a
è reale, si hanno i risultati compendiati nella tabella 8.1.
Table 8.1: Equazioni differenziali del primo ordine omogenee, con coeffciente
reale e costante
soluzioni oscillanti
mai
stabilit
quando
a ≤ 0
stabilità asintotica
quando
a < 0
Consideriamo ora l’equazione differenziale (8.26) a coefficienti reali. Introduciamo le
notazioni nella tabella 8.2, a sinistra. Ricordiamo infatti che se i coefficienti sono
reali, si ha in ogni caso
ℜeλ1 = ℜeλ2.
Con queste notazioni, le soluzioni (in forma reale) si esprimono come scritto nella
tabella 8.2, a destra mentre i risultati sulla stabilità per l’equazione (8.26),
quando i coefficienti sono reali, si leggono nella tabella 8.3.
Table 8.2: Secondo ordine, coefficienti reali e costanti. Sinistra: notazioni.
Destra: Equazioni del secondo ordine omogenee, soluzioni
Δ = b2 − 4c > 0 allora λ1 = −b+b2 −4c
2
λ2 = −b−b2 −4c
2
Δ = b2 − 4c = 0 allora λ
1 = λ2 = λ
Δ = b2 − 4c < 0 allora λ
1 = ξ + iω = λ̄2.
Δ > 0
αeλ1t + βeλ2t
Δ = 0
αeλt + βteλt
Δ < 0
Aeξt cos(ωt + ϕ)
Table 8.3: Secondo ordine, coefficienti reali e costanti
(e quindi ℜeλ1 = ℜeλ2.
Se gli autovalori sono reali allora λ1 = ℜeλ1,
λ2 = ℜeλ2)
soluzioni oscillanti
quando
Δ < 0
stabilità
quando
ℜeλ1 ≤ 0ℜeλ2 < 0 oppure
ℜeλ1 = ℜeλ2 = 0 ma λ1≠λ2
stabilità asintotica
quando
ℜeλ1 < 0,ℜeλ2 < 0
(non si esclude λ1 = λ2 < 0)
8.4 Manipolazioni usate nei corsi applicativi
Anche nel contesto delle equazioni differenziali, nei corsi di fisica e di
ingegneria verranno usate delle manipolazioni piuttosto “libere”, che è bene
capire.
Prima di tutto consideriamo un modo veloce per risolvere equazioni a variabili
separabili. La giustificazione di questo metodo è quella che noi abbiamo
illustrato al paragrafo 8.2. Consideriamo quindi l’equazione a variabili
separabili
x′ = g(t)f(x) ossiah(x(t))x′(t) = g(t) ove h(x) = 1
f(x).
Come si è visto, per trovarne le soluzioni, basta notare che
h(x(t))x′(t) = d
dtH(x(t))
ove H(x) è
primitiva di h(x).
E dunque
d
dtH(x(t)) = d
dxG(t)
con G(t)
primitiva di g(t).
Ora calcoliamo le primitive dei due membri. Il simbolo usato per indicare le primitive
di H(x)
è
H(x) = ∫
h(x)dx + c
e pensando di fare la sostituzione x = x(t)
(con x(t)
soluzione di cui ancora non conosciamo l’esistenza) si trova
∫
h(x)dx = ∫
h(x(t))dx(t) = ∫
h(x(t))x′(t)dt = ∫
g(t)dt.
Leggendo il primo e l’ultimo termine si trova che basta uguagliare
∫
h(x)dx = ∫
g(t)dt
e poi sostituire x con
la funzione incognita x(t),
Se uno dimentica che il segno di primitiva è
∫
dx,
da intendere come un unico simbolo indivisibile, potrebbe
sembrargli che questa formula sia stata ottenuta intendendo
x′ = dx
dt ; “moltiplicando
per dt” i
due membri dell’equazione differenziale e poi mettendo davanti a tutto il simbolo
∫
,
operazioni prive di senso. Nelle applicazioni, spesso si devono considerare sistemi di
equazioni differenziali. Per esempio, si considera il sistema
x′ = f(x,y)
y′ = g(x,y).
L’incognita è la coppia di funzioni (x(t),y(t)),
dipendente da una variabile t
che, come al solito, non si indica esplicitamente. Usando la notazione di Leibniz, la variabile
“nascosta” tviene
esplicitamente indicata almeno nel membro sinistro, e il sistema si scrive |
dxd t = f(x,y)
dyd t = g(x,y).
| (8.27) |
A questo punto i fisici dividono un’equazione per l’altra e “semplificano”
dt,
ottenendo
dy
dx = g(x,y)
f(x,y) ossiay′ = g(x,y)
f(x,y)
una sola equazione nell’incognita y,
e con la x
che è la variabile indipendente. La spiegazione di questo procedimento
è la seguente: supponiamo di aver trovato una soluzione
(x(t),y(t)) del sistema (8.27).
Se accade che x′(t
0)≠0
allora, almeno localmente, in un intorno di
t0, la
funzione t↦x(t)
è strettamente monotona e quindi invertibile. La sua funzione inversa
t = t(x) ha
derivata
dt
dx = t′(x) = 1
x′(t)con x = x(t).
Si può quindi costruire la funzione composta
y(t(x))
e
d
dxy(t(x)) = y′(t(x)) 1
x′(t(x)).
I valori di t
e di x
sono correlati da
x = x(t) ossiat = t(x)
e quindi (almeno localmente) y(t(x))
è funzione della sola x,
che viene indicata come y(x),
“nascondendo” t.
Quindi
scrivendo y(x) per y(t(x)) si hay′ = y′(x) = dy
dx = g(x,y)
f(x,y).
Va tenuto presente però che, a differenza delle pratiche descritte al paragrafo 3.4, questo
procedimento ha senso soltanto in un intorno di un punto assegnato: in generale, un dato
iniziale (x0,y0)
per cui f(x0,y0)≠0
(oppure g(x0,y0)≠0,
scambiando x
con y)
e che il risultato è corretto finché la traiettoria non incontra un punto in cui
f(x,y) si
annulla. Però, non c’è nessun modo di capire se e quando ciò accadrà,
guardando il dato iniziale.
8.5 Alcuni esercizi
- Dire quali delle equazioni differenziali seguenti sono scritte in forma normale,
quali sono a variabili separate e quali sono lineari:
|
x2y′ = (log x)y + sin x,x(y′)2 = (log x)y + sin x,x d
dx(y)2 = (log x)y + sin x,
x′ = x2 sin t, x′ = x sin t, x′ = x sin t + cos t.
|
- Identificare le soluzioni costanti delle equazioni differenziali a variabili
separabili seguenti, e spiegare se esse possono usarsi per studiare la
limitatezza delle altre soluzioni
|
x′ = (t3 − 1)(x3 − 1), y′ = (t3 − 1)(y2 − 1),
x′ = (t2 − 1)(x2 − 1), y′ = y(y2 − 1)(x2 − 4),
y′ = x(y2 − 1)(x2 − 4),y′ = xy2(y2 − 1)(x2 − 4).
|
E’ possibile avere anche qualche informazione sulla monotonia delle
soluzioni?
- Sapendo che x(t)
verifica
x′ = 3x2 − sin t,x(0) = 1
calcolarne le derivate prima, seconda e terza per
t = 0.
- Si consideri l’equazione differenziale
x′ = −2x2.
Sia x(t) la soluzione che
verifica x(0) = 1. Si vuol sapere
se esitono valori di α > 1
tali che questa soluzione verifichi anche
x(1) = α.
Si vuol sapere inoltre se esistono valori di
β > 0 tali che la
soluzione x(t)
verifichi x′(1) = β.
- Si determinino i domini massimali delle soluzioni dei
seguenti problemi di Cauchy. L’equazione differenziale è
x′ = −2x2
mentre la condizione di Cauchy è una delle seguenti:
|
x(0) = 0,x(1) = 0,x(0) = 1,
x(1) = 1,x(1) = 2,x(1) = −2.
|
- Si consideri l’equazione del moto armonico
(m > 0 indica la
massa e k > 0
è la costante elastica). Moltiplicando ambedue i membri per
x′(t)
si trovi la legge di conservazione dell’energia
1
2mv2 + 1
2kx2 = E = costante.
Si interpretino i due addendi che figurano in quest’uguaglianza.
- Si sappia che una funzione x(t)
definita su un intervallo verifica
|
1
2mv2 + 1
2kx2 = 1
2m x′(t) 2 + 1
2kx2(t) = E = costante.
| (8.29) |
Si mostri che la funzione x(t)
risolve l’equazione del moto armonico (8.28). Quindi le due equazioni (8.28)
e (8.29) “sono equivalenti” nel senso che hanno le medesime soluzioni. Si noti
però che una è scritta in forma normale e l’altra no.
- Si considerino le funzioni y(t) = αt2,
con α
parametro reale.
- Si mostri che ciascuna di queste funzioni risolve l’equazione
differenziale y′ = 2y∕t.
Si noti che l’equazione differenziale non è definita per t = 0,
ma le soluzioni dell’equazione hanno estensione continua a t = 0.
Cosa si nota se si prova ad imporre la condizione di Cauchy
y(0) = 0?
- Esistono soluzioni dell’equazione che verificano lim t→0+y(t) = 1?
- (⋆) Per
t > 0 si consideri l’equazione
differenziale y′ = −y∕t2.
Si vuol sapere se esistono soluzioni dell’equazione differenziale tali che
lim t→0+y(t) = +∞ oppure
lim t→0+y(t) = c ∈ ℝ.
- (⋆)
Si vuole un’equazione differenziale soddisfatta da una funzione
f(x)
che gode di questa proprietà, che deve valere salvo un numero finito di valori
x0: la
tangente in (x0,f(x0))
al grafico della funzione incontra l’asse delle ascisse in un punto
x che deve
verificare x∕x0 = c,
con c numero
indipendente da x0
(se c = 2
si confronti con l’esercizio 15 del Cap. 3).
- (⋆) Per
t > 0 si consideri l’equazione
differenziale y′ = −(tan y)∕t2. Si
imponga la condizione y(1) = π∕2
(si noti che il secondo membro non è definito per
y = π∕2.
Si mostri che esiste una soluzione che verifica questa condizione, ma che il suo
dominio di esistenza massimale non è un intervallo aperto.
- Al variare del parametro reale α
si studi la stabilità dell’equazione differenziale
y″ = −y − αy′.
- Si consideri l’equazione differenziale
y″ = −y − αy′ + sin t con
α≠0.
Si mostri che una soluzione particolare è
y(t) = −(1∕α) cos t
e si calcoli una soluzione particolare quando
α = 0.
- (⋆)
Si considerino l’osservazione 166 e l’esempio 170. Si spieghi
perchè l’argomento nell’osservazione 166 non si applica
al caso dell’esempio 170 (quante soluzioni ha l’equazione
(3∕2)x2∕3 = t?).
Si usi la spiegazione trovata per costruire una terza soluzione del problema di
Cauchy all’esempio 170.
- (⋆)
Siano x(t)
ed y(t)
due soluzioni diverse del medesimo problema di Cauchy (8.5), definite sullo stesso
intervallo
[t0,T].
Calcolando le primitive dei due membri di (8.5), si ha
x(t) = x0 + ∫
0tg(s)f(x(s))ds,y(t) = x
0 + ∫
0tg(s)f(y(s))ds.
Usando la proprietà di monotonia del calcolo delle
primitive (esercizio 21 del Capitolo 4) si ottenga per
0 ≤ t ≤ T
|x(t) − y(t)|≤∫
0t|g(s)|f(x(s)) − f(y(s)) ds.
Si deduca, usando l’esercizio 23 del Capitolo 4, che
|x(t) − y(t)|≤ T(HK)M
con M = max [0,T]|x(t) − y(t)|,
H = max [0,T]|g(t)|,
K = max [0,T]|f′(x)|.
Si spieghi perché questa disuguaglianza non può valere se il numero
T è stato scelto
in modo che sia THK < 1∕2
e se x(t)
e y(t)
sono diverse. Ciò mostra che, se valgono le ipotesi del Teorema di
Cauchy, i grafici di due soluzioni diverse non possono intersecarsi,
nemmeno se una delle due soluzioni è costante (caso non considerato
nell’osservazione 166).
- Si xonsideri il problema di Cauchy
x′ = 1∕x,
x(0) = 1.
Si mostri che la soluzione è definita per
t > −1 e se ne studi
il limite per t →−1+.
Si spieghi la relazione di quanto trovato col Teorema 172.
Capitolo 9
Integrali definiti ed impropri
Erano tali per me queste angustie che sopraggiunta
l’invasione dei Francesi, e nella età di soli 20
anni correndo pericolo della libertà e della vita,
in quelli orribili frangenti dicevo fra me “questo
tuttavia è meno male che lo stare alla scuola”.
Monaldo Leopardi, Autobiografia.
L’integrale è un numero che si associa ad una funzione definita su un intervallo (e
dotata di opportune proprietà). Nel caso che la funzione prenda valori positivi, il
suo integrale definisce l’area della parte di piano compresa tra il grafico e l’asse delle
ascisse.
9.1 La definizione dell’integrale
Sia f(x)
una funzione limitata e definita su un intervallo
[a,b]. Dunque, assumiamo
che esista un numero M
tale che |f(x)| < M per ogni
x ∈ [a,b]. Si noti che non
richiediamo che la funzione f(x)
prenda valori maggiori o uguali a zero. chiamiamo trapezoide individuato dalla funzione
f(x) l’insieme
dei punti (x,y)
tali che
a ≤ x ≤ b,e f(x) ≤ y ≤ 0 sef(x) ≤ 0 0 ≤ y ≤ f(x) se f(x) ≥ 0,
si veda la figura 9.1, nella quale [a,b] = [0, 6].
Il trapezoide è la parte di piano tratteggiata.
Vogliamo definire un numero che corrisponda al concetto intuitivo di area del
trapezoide di f(x),
se f(x) prende
valori non negativi; oppure, in generale, alla differenza tra le aree della parte di trapezoide
sopra l’asse delle ascisse e di quella che sta sotto. Per questo, suddividiamo l’intervallo
[a,b] con un numero finito di
punti equidistanti.
|
a = x0 < x1 < x2 < ⋯ < xn−2 < xn−1 < xn = b,
con xk = a + kb−a
n , 0 ≤ k ≤ n .
|
In questo modo,
[a,b] = [x0,x1) ∪ [x1,x2) ∪⋯ ∪ [xn−2,xn−1) ∪ [xn−1,xn].
Abbiamo cioè costruito una partizione di
[a,b] di tipo particolare:
abbiamo rappresentato [a,b]
come unione di intervalli (disgiunti) chiusi a sinistra ed aperti a
destra (salvo l’ultimo che è anche chiuso a destra). Indichiamo con
𝒫n la
partizione introdotta sopra e chiamiamo finezza della partizione il numero
δn = (b − a)∕n, che
è la distanza tra due punti consecutivi della partizione. Data la partizione
𝒫n, indichiamo
con mi
ed Mi i
numeri
mi = inf x∈[xi,xi+1)f(x),
Mi = sup x∈[xi,xi+1)f(x).
Ricordiamo che la funzione f(x)
è limitata: |f(x)| < M. Dunque,
per ogni indice i
si ha:
−M ≤ mi ≤ Mi ≤ M.
Associamo ora alla partizione 𝒫n
due numeri, sn
ed Sn, |
sn = ∑
i=0n−1m
i(xi+1 − xi) = b−a
n ∑
i=0n−1m
i,
Sn = ∑
i=0n−1M
i(xi+1 − xi) = b−a
n ∑
i=0n−1M
i.
| (9.1) |
Questi numeri rappresentano somme di “aree” di rettangoli, l’area
essendo presa col segno negativo se il rettangolo è sotto l’asse delle
ascisse. La figura 9.2 illustra i rettangoli che si usano per costruire la
sn quando i punti di
divisione xi sono i numeri
interi i. Si faccia la
figura analoga per Sn.
E’ chiaro che |
−M(b − a) ≤ sn ≤ Sn ≤ M(b − a)
| (9.2) |
(la disuguaglianza intermedia segue dal fatto che ciascun addendo di
sn
è minore o uguale all’addendo corrispondente di
Sn). Per
per la proprietà di Dedekind esistono i numeri
s = sup n{sn},S = inf n{Sn}.
Si potrebbe provare che |
s ≤ SossiaS − s ≥ 0.
| (9.3) |
Più precisamente:
−M(b − a) ≤ sn ≤ s = sup n{sn}≤ inf n{Sn} = S ≤ Sn ≤ M(b − a).
DEfiNIZIONE DI INTEGRALE DI RIEMANN
Sia
f(x)
una funzione definita su un intervallo
[a,b]
e limitata. Se accade che
s = Sossias = sup n{sn} = inf n{Sn} = S
il numero s = S
si chiama integrale di Riemann (o semplicemente integrale) di
f(x)
su [a,b];
e la funzione f(x)
si dice integrabile su [a,b].
L’integrale di Riemann si chiama anche integrale definito
L’integrale di Riemann di f(x)
su [a,b] si
indica col simbolo
∫
abf(x)dx.
Osservazione 177 Si noti il contrasto tra i termini integrale definito ed
integrale indefinito. Il primo indica un numero mentre il secondo indica
l’insieme di tutte le primitive di f(x). ■
Usando la definizione, si verifichi che una funzione costantemente uguale a
c su
[a,b] ha integrale
uguale a c ⋅ (b − a),
ossia uguale all’area del rettangolo di base
[a,b] ed altezza
c, se
c ≥ 0; all’opposto
dell’area se c < 0.
L’integrale ∫
abf(x)dx
si interpreta come area del trapezoide quando accade che
f(x) ≥ 0; come
differenza tra l’area della parte di trapezoide che sta sopra l’asse delle ascisse e
quella che sta sotto altrimenti.
Osservazione 178 (Sulla notazione) La notazione ∫
abf(x)dx
ha una ragione storica e va presa come unico blocco: non si possono separare
∫
ab
e dx.
Anzi, sarebbe anche lecito scrivere semplicemente ∫
abf
invece di ∫
abf(x)dx.
Il simbolo più complesso aiuta a ricordare certe formule che vedremo, sia in
questo che in corsi successivi. Inoltre, sottolineiamo che ∫
abf(x)dx
è un numero. La “variabile” x
non ha alcun ruolo e si chiama la variabile muta d’integrazione “Muta” nel
senso che il simbolo prescelto per essa non influisce sul valore dell’integrale, e
può essere cambiato a piacere. Quindi,
∫
abf(x)dx = ∫
abf(s)ds = ∫
abf(y)dy = ∫
abf(ξ)dξ…
E’ però importante capire subito un uso della variabile muta d’integrazione e
del simbolo dx.
Talvolta si ha una famiglia di funzioni x↦f(x,y),
una funzione di x ∈ [a,b]
per ogni valore del parametro y.
Può essere necessario integrare ciascuna di queste funzioni, ottenendo un
numero per ogni valore di y;
ossia ottenendo una funzione della variabile y:
Φ(y) = ∫
abf(x,y)dx.
E’ la presenza della notazione dx
che ci dice quale è la variabile muta d’integrazione e quale è il parametro. ■
Esempio 179 Quest’esempio mostra la debolezza della definizione che
abbiamo scelto: per calcolare
∫
abcdx = c(b − a)
basta usare un solo rettangolo. Non c’è nessun bisogno di suddividere
il trapezoide in “tanti” rettangoli. Ciò fa capire che dovendo calcolare
numericamente l’integrale di una funzione il cui grafico è quello in figura 9.3,
a sinistra, converrà usare una partizione non uniforme dell’intervallo [a,b],
mettendo pochi punti di suddivisione dove la funzione è circa costante
e tanti punti dove varia velocemente. La figura 9.3, a destra, mostra
che un metodo ancora più effciente consiste nell’approssimare l’area da
calcolare mediante trapezi, invece che mediante rettangoli. Nella figura a
destra abbiamo disegnato i trapezi usando meno punti di suddivisione
di quanti ne avessimo usati per i rettangoli per non confondere il lato
del trapezio col grafico della funzione; e ciò nonostante è evidente che
l’approssimazione mediante “pochi” trapezi è migliore di quella con “tanti”
rettangoli. ■
Una definizione più generale. L’esempio 179 mostra l’utilità per il calcolo
numerico di approssimare il valore dell’integrale mediante partizioni dell’intervallo
[a,b] ottenute
con punti non equidistanti. Si potrà quindi cercare di ripetere la costruzione
dell’integrale usando partizioni con punti non equidistanti, costruendo le somme
s ed
S con formule analoghe
a quelle delle sn
ed Sn e
mandando a zero la finezza della partizione, ossia la massima delle distanze tra i
punti consecutivi della partizione. Potrebbe venire il dubbio che in questo modo
si ottenga un numero diverso da quello che si trova mediante partizioni
con punti equidistanti. Senza indugiare a provarlo, diciamo che ciò non
accade.
9.1.1 Proprietà dell’integrale
Le proprietà cruciali dell’integrale sono la linearità, la monotonia e
l’additività.
Linearità dell’integrale. In generale si chiama “lineare” una
trasformazione che si distribuisce sulla somma e da cui “si portano
fuori” le costanti moltiplicative; ossia una trasformazione, diciamo
𝒥, con
questa proprietà:
𝒥 αf + βg = α𝒥f + β𝒥g.
L’integrale di Riemann ha questa proprietà. Infatti, vale:
Teorema 180 Siano
f(x)
e
g(x)
due funzioni integrabili sul medesimo intervallo
[a,b]
e siano
α
e
β
due numeri reali. In tal caso la funzione
αf(x) + βg(x)
è integrabile su
[a,b]
e inoltre vale
∫
ab αf(x) + βg(x) dx = α∫
abf(x)dx + β∫
abg(x)dx.
La dimostrazione non è diffcile ma un po’ macchinosa. Questa proprietà si chiama
linearità dell’integrale Ricordiamo che
f+(x) = max{f(x), 0},f−(x) = min{f(x), 0}
da cui
f(x) = f+(x) + f−(x),|f(x)| = f+(x) − f−(x).
Si potrebbe provare:
Teorema 181 La funzione f(x),
limitata su (a,b),
è integrabile se e solo se sono integrabili ambedue le funzioni f+(x)
ed f−(x).
Ciò combinato con la proprietà di linearità dell’integrale dà:
Teorema 182 Se f(x)
è integrabile su [a,b]
allora |f(x)|è
integrabile su [a,b].
Inoltre, valgono le uguaglianze |
∫
abf(x)dx = ∫
abf
+(x)dx + ∫
abf
−(x)dx,
∫
ab|f(x)|dx = ∫
abf
+(x)dx −∫
abf
−(x)dx.
|
Monotonia dell’integrale. E’ pressoché immediato dalla definizione di
integrale:
Teorema 183 Sia
f(x)
integrabile e positiva. Allora,
∫
abf(x)dx ≥ 0.
Sia ora
g(x) ≤ f(x) ossiaf(x) − g(x) ≥ 0.
Usando la linearità si vede che
0 ≤∫
ab f(x) − g(x) dx = ∫
abf(x)dx −∫
abg(x)dx.
Dunque:
Corollario 184 Se f(x)
e g(x)
sono integrabili sul medesimo intervallo [a,b]
e se g(x) ≤ f(x)
per ogni x ∈ [a,b],
allora si ha
∫
abg(x)dx ≤∫
abf(x)dx.
Questa proprietà si chiama monotonia dell’integrale Usando l’integrabilità del valore
assoluto (Teorema 182) e la disuguaglianza
−|f(x)|≤ f(x) ≤|f(x)|
si trova
∫
abf(x)dx ≤∫
ab|f(x)|dx.
Additività dell’integrale. Sia f(x)
definita su [a,b]
e sia c ∈ (a,b).
Vale
Teorema 185 La funzione
f(x)
è integrabile su
[a,b]
se e solo se è integrabile sia su
[a,c]
che su
[c,d]
e in tal caso si ha
∫
abf(x)dx = ∫
acf(x)dx + ∫
cbf(x)dx.
Questa proprietà si chiama additività dell’integrale Grazie
a questo teorema, possiamo definire la funzione integrale di
f(x). Sia
f(x) integrabile
su [a,b]. Per
ogni x ∈ (a,b]
calcoliamo la funzione
F(x) = ∫
axf(s)ds.
Poniamo inoltre
F(a) = 0
cosìche F(x) è
definita su [a,b]. La
funzione F(x) si chiama la
funzione integrale di f(x).
Integrale ed operazioni. La proprietà di linearità mostra
le relazioni tra le operazioni di somma e di moltiplicazione per
costanti e il calcolo dell’integrale. Il Teorema 182 mostra che se
f(x) è integrabile
allora f+(x),
f−(x) e
|f(x)|
sono integrabili, senza dare modo di calcolarne l’integrale. Vale anche:
Teorema 186 Si ha:
- se f(x)
e g(x)
sono integrabili su [a,b]
anche f(x)g(x)
è integrabile su [a,b];
- se f(x)
e g(x)
sono integrabili su [a,b]
e inoltre se g(x)
è continua e non si annulla su [a,b],
allora anche f(x)∕g(x)
è integrabile su [a,b].
Va detto però che non c’è alcuna relazione semplice tra gli integrali di due
funzioni e quello del loro prodotto o del loro quoziente.
9.1.2 Classi di funzioni integrabili
Valgono i due teoremi seguenti:
Teorema 187 Se f(x)
è continua sull’intervallo limitato e chiuso [a,b],
essa è integrabile su [a,b]
e quindi su ciascun suo sottointervallo.
Teorema 188 Se f(x)
è monotona sull’intervallo limitato e chiuso [a,b],
essa è integrabile su [a,b]
e quindi su ciascun suo sottointervallo.
Combinando questi teoremi con la proprietà di additività dell’integrale, segue che se
l’intervallo [a,b]
è unione di due o più sottointervalli su ciascuno dei quali la
funzione ha restrizione continua oppure monotona, allora la funzione
f(x) è integrabile su
[a,b]. Dimostrazione
del Teorema 188. Supponiamo per fissare le idee che la funzione sia crescente su
[a,b]. Notiamo che la
funzione è limitata su [a,b].
Infatti vale
f(a) ≤ f(x) ≤ f(b).
Suddividiamo l’intervallo [a,b]
in n parti
uguali [xi,xi+1) e
consideriamo le somme (9.1), ossia |
sn = ∑
i=0n−1m
i(xi+1 − xi) ove mi = inf x∈[xi,xi+1)f(x),
Sn = ∑
i=0n−1M
i(xi+1 − xi)ove Mi = sup x∈[xi,xi+1)f(x).
|
cosìche
mi = f(xi),Mi ≤ f(xi+1).
Ricordiamo che l’integrale esiste se
s = Sove s = sup n{sn}, S = inf n{Sn}
e che in generale (si veda la (9.3)):
0 ≤ S − s.
Dobbiamo quindi provare che la differenza
S − s non è strettamente
positiva. Ossia, dobbiamo
provare che per ogni 𝜖 > 0
vale
0 ≤ S − s < 𝜖.
Notiamo che
sn ≤ s ≤ S ≤ Sn⇒0 ≤ S − s ≤ Sn − sn.
Dunque, basta provare che per ogni 𝜖 > 0
esiste un opportuno N = N𝜖
tale che
SN − sN < 𝜖.
Si ricordi che l’intervallo [a,b]
si è diviso in n
parti uguali, ossia xi+1 − xi = (b − a)∕n.
Dunque si ha |
Sn − sn = ∑
i=0n−1(M
i − mi)(xi+1 − xi) = b − a
n ∑
i=0n−1(M
i − mi)
= b − a
n ∑
i=0n−1 M
i − f(xi) ≤b − a
n ∑
i=0n−1 f(x
i+1) − f(xi)
= b − a
n [ f(x1) − f(x0) + f(x2) − f(x1) + ⋯
+ f(xn−1) − f(xn−2) + f(xn) − f(xn−1) ] = b − a
n f(b) − f(a) .
|
Queste relazioni valgono per ogni n.
fissato 𝜖 > 0
esiste N
tale che
b − a
N f(b) − f(a) < 𝜖
e quindi vale
0 ≤ S − s ≤ SN − sN ≤ 𝜖,
come volevamo. ■
9.1.3 La media integrale
Sia f(x)
integrabile su [a,b]
e sia
m = inf [a,b]f(x),M = sup [a,b]f(x).
Consideriamo le due funzioni
h(x) ≡ m,k(x) ≡ M
cosìche
h(x) ≤ f(x) ≤ k(x).
La monotonia dell’integrale mostra che
m(b − a) = ∫
abh(x)dx ≤∫
abf(x)dx ≤∫
abk(x)dx = M(b − a);
ossia esiste c ∈ (m,M)
tale che:
c(b − a) = ∫
abf(x)dx.
Il numero c
è ovviamente definito da
c = 1
b − a∫
abf(x)dx.
La sua proprietà essenziale è di essere compreso tra
inf [a,b]f(x) e
sup [a,b]f(x). Il numero
c si chiama la
media integrale di f(x).
Sia ora f(x)
continua su [a,b].
Ricordando il teorema dei valori intermedi si ha:
Teorema 189 Se f(x)
è continua su [a,b],
la sua media integrale è uno dei valori della funzione; ossia esiste x0 ∈ [a,b]
tale che
(b − a)f(x0) = ∫
abf(x)dxossiaf(x
0) = 1
b − a∫
abf(x)dx.
Se f(x) ≥ 0,
il significato del numero c,
media integrale di f(x)
su [a,b],
è il seguente: il numero c
è l’altezza del rettangolo di base
[a,b],
la cui area è uguale a quella del trapezoide. Ciò è illustrato in
figura 9.4. La figura mostra anche la bisettrice del primo quadrante che non
ha alcun ruolo nella media integrale. E’ disegnata solo per sottolineare il fatto
che l’unità di misura è la medesima sui due assi.
9.2 Integrale orientato
Nel simbolo dell’integrale di Riemann
∫
ab
necessariamente a ≤ b.
Vogliamo ora definire questo simbolo anche nel caso
a > b. Ciò
si fa semplicemente ponendo
∫
abf(x)dx = −∫
baf(x)dx.
Uno dei due membri è definito e l’uguaglianza definisce l’altro. Si noti che se
a = b si
trova
∫
aaf(x)dx = 0.
L’integrale
∫
abf(x)dx
cosìintrodotto, senza che debba essere
a ≤ b, si
chiama integrale orientato Per esso valgono tutte le proprietà viste per l’integrale
di Riemann, salvo la monotonia che richiede un po’ di cautela, perché le
disuguaglianze cambiano verso quando si cambia segno ai due membri.
Quindi:
la disuguaglianza
∫
abf(x)dx ≤∫
ab|f(x)|dx
NON VALE PER L’INTEGRALE ORIENTATO perché il secondo
membro può essere negativo ed il primo positivo. Essa va sostituita
da
∫
abf(x)dx ≤∫
ab|f(x)|dx.
Invece, la definizione della media integrale rimane la stessa anche
per l’integrale orientato: la media integrale sull’intervallo di estremi
x0
ed
x1
è
1
x1 − x0 ∫
x0x1
f(s)ds
e tale numero è compreso tra l’estremo inferiore e l’estremo
superiore dei valori che la funzione prende sull’intervallo di estremi
x0
ed x1,
sia quando x0 < x1
che quando x1 < x0.
Invece, per l’integrale orientato vale la proprietà di additività
∫
abf(x)dx = ∫
acf(x)dx + ∫
cbf(x)dx
senza alcun vincolo sull’ordine dei tre numeri
a,
b e
c.
Usando ciò, si può definire la funzione integrale
F(x) = ∫
axf(s)ds
sia per x ≥ a che per
x < a (ovviamente,
se è definita f(x)).
Infatti
F(x) = ∫
axf(s)ds = ∫
axf(s)ds sex ≥ a
(∫
ax indica l’integrale di Riemann),
−∫
xaf(s)ds sex < a
(∫
xa indica l’integrale di Riemann).
In particolare,
Teorema 190 Se
f(x) ≥ 0
è definita su
ℝ
e positiva, la funzione
F(x) = ∫
axf(s)ds
è crescente su ℝ.
9.3 La funzione integrale
Ricordiamo che se f(x)
è integrabile su [a,b]
essa è integrabile su ogni sottointervallo. In particolare è integrabile su
[a,x]
e quindi possiamo definire la funzione integrale di
f(x), ossia
la funzione
F(x) = ∫
axf(s)dsx ∈ (a,b],F(a) = 0.
Se accade che la funzione f(x) è
definita anche a sinistra di a,
la funzione integrale si definisce anche a sinistra di
a,
facendo intervenire l’integrale orientato:
se x < a alloraF(x) = ∫
axf(s)ds = −∫
xaf(s)ds.
Se la funzione f(x)
ha segno costante, la funzione integrale è monotona:
Teorema 191 Se
f(x)
è positiva la funzione integrale è crescente mentre se
f(x)
è negativa allora la funzione integrale è decrescente.
Dim. Proviamo la crescenza, supponendo che
f(x) sia positiva. Sia
x1 < x2 e proviamo che
F(x1) ≤ F(x2). Ciò è ovvio se
x1 < a < x2 perché in tal caso
F(x1) ≤ 0 ≤ F(x2). Quindi consideriamo
i due casi a ≤ x1 < x2
ed x1 < x2 ≤ a:
-
- caso a ≤ x1 < x2:
usando l’additività dell’integrale si ha
F(x2) = ∫
ax2
f(s)ds = ∫
ax1
f(s)ds + ∫
x1x2
f(s)ds ≥∫
ax1
f(s)ds = F(x1)
perché ∫
x1x2f(s)ds ≥ 0.
-
- caso x1 < x2 ≤ a: la
definizione di integrale orientato e l’additività dell’integrale danno
|
∫
ax1
f(s)ds = −∫
x1af(s)ds = −∫
x1x2
f(s)ds + ∫
x2af(s)ds
= −∫
x1x2
f(s)ds −∫
x2af(s)ds = −∫
x1x2
f(s)ds + ∫
ax2
f(s)ds
= −∫
x1x2
f(s)ds + F(x2) ≤ F(x2)
|
perché x1 < x2 e quindi
−∫
x1x2f(s)ds ≤ 0. ■
Proviamo il lemma seguente:
Lemma 192 Sia f(x)
integrabile su [a,b]
e sia x0 ∈ [a,b].
Si ha:
lim h→0 ∫
x0x0+hf(s)ds = 0
(se x0 = a
allora h > 0
mentre se x0 = b
allora h < 0).
Dim. Ricordiamo che una funzione integrabile è per definizione limitata:
|f(x)|≤ M∀x ∈ [a,b].
Dunque si ha
0 ≤∫
x0x0+hf(s)ds ≤∫
x0x0+h|f(s)|ds ≤∫
x0x0+hMds = M|h|.
L’asserto segue dal teorema di confronto dei
limiti. ■
Conseguenza di questo risultato è che la funzione integrale è continua anche
se f(x)
può non essere continua:
Teorema 193 La funzione F(x)
è continua su [a,b].
Dim. Va provato:
lim h→0 ∫
ax0+hf(s)ds −∫
ax0
f(s)ds = 0
(se x0 = a
oppure x0 = b
allora h > 0
oppure h < 0).
L’additività dell’integrale permette di scrivere |
∫
ax0+hf(s)ds −∫
ax0
f(s)ds = ∫
ax0
f(s)ds + ∫
x0x0+hf(s)ds −∫
ax0
f(s)ds
= ∫
x0x0+hf(s)ds→0
|
per il Lemma 192, come si voleva. ■
Proviamo ora:
Lemma 194 Sia f(x)
continua in x0 ∈ [a,b].
Allora,
lim h→0 1
h∫
x0x0+hf(s)ds = f(x
0).
Dim. Va provato che per ogni 𝜖 > 0
esiste δ > 0 tale
che se |h| < δ
si ha |
f(x0) − 𝜖 < 1
h∫
x0x0+hf(s)ds < f(x
0) + 𝜖.
| (9.4) |
Usando la continuità di f(x)
in x0 si trova:
per ogni 𝜖 > 0
esiste δ > 0 tale
che se s ∈ (x0 − δ,x0 + δ)
si ha:
f(x0) − 𝜖 < f(s) < f(x0) + 𝜖.
Scegliamo h con
|h| < δ. La monotonia
dell’integrale dà (sia se h > 0
che se h < 0,
usando la definizione di integrale orientato):
1
h∫
x0x0+h f(x
0) − 𝜖ds ≤ 1
h∫
x0x0+hf(s)ds ≤ 1
h∫
x0x0+h f(x
0) + 𝜖ds
ossia, se |h| < δ
si ha
f(x0) − 𝜖 ≤ 1
h∫
x0x0+hf(s)ds ≤ f(x
0) + 𝜖,
che è quanto volevamo provare. ■
Se f(x)
è una funzione integrabile qualsiasi, la funzione
F(x) può non essere
derivabile. Invece, se f(x)
è continua la funzione F(x)
è derivabile:
Teorema 195 (Teorema fondamentale del calcolo integrale) Se f(x)
è continua su [a,b],
la funzione F(x)
è derivabile su (a,b)
e vale
F′(x) = f(x)∀x ∈ (a,b),F
+′(a) = f(a),F
−′(b) = f(b).
Ossia, la funzione integrale di una funzione continua
f(x) ammette
derivata in ogni
punto di [a,b], ed
F′(x) è la funzione
integranda f(x).
Di conseguenza,
Corollario 196 Ogni funzione continua su un intervallo ammette primitive.
Dimostrazione del Teorema 195. La funzione
f(x) è continua
su [a,b]
e quindi il Lemma 194 può applicarsi in ciascun punto di
[a,b]. Dunque,
per ogni x ∈ [a,b]
si ha: |
f(x) = lim h→0 1
h∫
xx+hf(s)ds = lim
h→0 1
h ∫
ax+hf(s)ds −∫
axf(s)ds
= lim h→0 1
h F(x + h) − F(x) = F′(x)
|
(intendendo che F′(x) indica la derivata
destra se x = a e la derivata sinistra se
x = b). ■
L’importanza pratica di questo risultato sta nel fatto che, se
f(x) è
continua, il calcolo dell’integrale definito può ottenersi tramite il calcolo delle primitive.
Ossia, la F(x),
funzione integrale, è una particolare primitiva di
f(x): è quella primitiva
che si annulla in a.
Ricordiamo ora che due primitive diverse su un intervallo
(a,b) di
una medesima funzione hanno differenza costante. Quindi, se mediante le
tecniche di calcolo delle primitive, si è trovata una qualsiasi primitiva
F(x) della funzione
continua f(x),
si ha:
∫
abf(x)dx = F(b) − F(a).
Lo scarto F(b) − F(a)
si indica anche col simbolo
Fab
e quindi si scrive
∫
abf(x)dx = F
ab.
9.3.1 Integrazione per sostituzione
Il teorema fondamentale del calcolo integrale permette di correlare integrali
calcolati mediante trasformazioni del dominio di integrazione. Sia
f(x) continua
su [a,b] e
sia F(x)
una sua primitiva. Come si è visto, |
∫
abf(x)dx = F(b) − F(a).
| (9.5) |
Sia ϕ(t) una funzione
continua su un intervallo [α,β]
e derivabile su (α,β).
Supponiamo inoltre che ϕ([α,β]) ⊆ [a,b].
Quindi esistono punti c
e d in
[a,b] tali
che
ϕ(α) = c,ϕ(β) = d.
E’
d
dtF(ϕ(t)) = F′(ϕ(t))ϕ′(t) = f(ϕ(t))ϕ′(t)
e quindi
F(ϕ(β)) − F(ϕ(α)) = ∫
αβf(ϕ(t))ϕ′(t)dt.
Ma,
F(ϕ(β)) − F(ϕ(α)) = F(d) − F(c) = ∫
cdf(x)dx
e quindi si ha anche
∫
cdf(x)dx = ∫
αβf(ϕ(t))ϕ′(t)dt
ossia |
∫
αβf(ϕ(t))ϕ′(t)dt = ∫
ϕ(α)ϕ(β)f(x)dx.
| (9.6) |
Si noti che questa formula vale in generale per l’integrale orientato. Anzi,
anche se l’integrale a sinistra di (9.6) è un’integrale di Riemann, può ben
essere che gli estremi dell’integrale di destra coincidano o anche che sia
ϕ(α) > ϕ(β).
Osservazione 197
Se l’integrale da calcolare è (9.5) allora dovremo identificare un intervallo
[α,β]
ed una trasformazione
ϕ(t)
tale che
ϕ(α) = a
e
ϕ(β) = b
(o viceversa) e tale che l’integrale a sinistra in (9.6) sia più facile
da calcolare di quello a destra. Non abbiamo richiesto che la funzione
ϕ(t)
sia iniettiva. Se lo è allora la formula (9.6) si può scrivere nella forma
∫
abf(x)dx = ∫
ϕ−1(a)ϕ−1(b)f(ϕ(t))ϕ′(t)dt. ■
9.4 Integrale improprio
Si chiama integrale improprio quello che si ottiene estendendo l’integrale di
Riemann a funzioni dotate di asintoto verticale oppure definite su una semiretta (o
ambedue le cose) mediante il calcolo di un limite. Conviene vedere separatamente i
due casi seguenti, che verranno poi combinati insieme. Introduciamo un termine: sia
f(x) definita su
un intervallo (a,b),
limitato o meno. Non si richiede che la funzione sia limitata. La funzione
f(x)
si dice localmente integrabile quando è integrabile (nel
senso di Riemann e quindi anche limitata) su ogni intervallo
[c,d] limitato e chiuso
contenuto in (a,b).
9.4.1 L’integrale su una semiretta
Consideriamo una funzione f(x)
definita sulla semiretta [a, +∞)
ed integrabile (nel senso di Riemann e quindi limitata) su ogni intervallo
[a,T]. E’
cosìpossibile definire la funzione
F(T) = ∫
aT f(x)dx
Consideriamo
lim T→+∞F(T).
Se questo limite esiste, finito o meno, si definisce
∫
a+∞f(x)dx = lim
T→+∞F(T)
e si chiama integrale improprio (su (a, +∞))
di f(x). Si
hanno i casi elencati nella tabella 9.1
Table 9.1: I casi dell’integrale improprio
Se
l'integrale improprio
si dice
si scrive
lim T→+∞∫
aT f(x)dx = l ∈ ℝ
integrale convergente
∫
a+∞f(x)dx = l
lim T→+∞∫
aT f(x)dx = ±∞
integrale divergente
∫
a+∞f(x)dx = ±∞
lim T→+∞∫
aT f(x)dx non esiste
non esiste indeterminato oscillante
9.4.2 L’integrale in presenza di un asintoto verticale
Supponiamo che la funzione f(x)
sia definita su (a,b] ed abbia
asintoto verticale x = a:
lim x→a|f(x)| = +∞.
Supponiamo inoltre che sia localmente integrabile su
(a,b]. In
questo caso, si può definire la funzione
F(𝜖) = ∫
𝜖bf(x)dx
per ogni 𝜖 ∈ (a,b] e si può
studiarne il limite per 𝜖 → a+.
Se questo limite esiste lo indicheremo col simbolo
∫
abf(x)dx = lim
𝜖→a+ ∫
𝜖bf(x)dx
e lo chiameremo ancora integrale improprio su
(a,b).
Se il limite è finito diremo che l’integrale improprio converge; se è
+∞ oppure
−∞ diremo
che diverge. Se il limite non esiste, diremo che l’integrale improprio non esiste
(equivalentemente, oscilla o è indeterminato). Ossia, per l’integrale improprio su
(a,b] si
può fare una tabella analoga alla 9.1.
9.4.3 Casi più generali
I due casi precedenti possono combinarsi tra loro. Per esempio:
- se f(x)
è localmente integrabile su (a, +∞),
si possono studiare i due limiti
lim 𝜖→a ∫
𝜖cf(x)dx, lim
T→+∞∫
cT f(x)dx
con lo stesso c.
Usando l’additività dell’integrale, si mostra che se i due limiti esistono
finiti o infiniti di segno concorde la loro somma non dipende dalla
scelta di c ∈ (a, +∞)
e si scrive
∫
a+∞f(x)dx = lim
𝜖→a ∫
𝜖cf(x)dx + lim
T→+∞∫
cT f(x)dx.
- in modo analogo si procede se la funzione ha più asintoti verticali;
- in modo analogo, se f(x)
è localmente integrabile su ℝ,
scriveremo
∫
−∞+∞f(x)dx = lim
S→−∞∫
Scf(x)dx + lim
T→+∞∫
cT f(x)dx
(i limiti devono essere finiti o infiniti di segno concorde). E’ importante
sottolineare che i due limiti, per S →−∞
e per T → +∞,
vanno calcolati indipendentemente. Per esempio, la funzione f(x) = arctan x
non ha integrale improprio su ℝ
perché i due limiti precedenti sono il primo −∞
e il secondo +∞.
Però,
lim T→+∞∫
−T T arctan xdx = 0
perché la funzione è dispari e quindi
∫
−T T arctan xdx = 0
per ogni T.
9.5 Criteri di convergenza per integrali impropri
In pratica, il calcolo di un integrale improprio è diffcile e non si riesce a fare
esplicitamente. Si danno però dei criteri che assicurano la convergenza o
divergenza dell’integrale, che conviene esaminare prima nel caso di funzioni
positive.
9.5.1 Criteri di convergenza: funzioni positive su semirette
Per fissare le idee, supponiamo di lavorare su una semiretta verso destra,
[a, +∞)
e di avere una funzione che prende valori maggiori o uguali
a zero e che è integrabile su ogni intervallo limitato
[a,b].
Consideriamo la funzione
T↦∫
aT f(x)dx.
Questa è una funzione crescente di
T perché
la f(x) è
positiva. Quindi, per il teorema delle funzioni monotone,
lim T→+∞∫
aT f(x)dx
esiste, finito o meno. Dunque,
Teorema 198 Se la funzione
f(x)
prende valori maggiori o uguali a zero, l’integrale improprio
∫
a+∞f(x)dx
converge oppure diverge. Esso non può essere oscillante.
Quindi, se possiamo dire che esiste M
tale che
∫
aT f(x)dx < M
per ogni T
allora l’integrale converge; se invece la funzione di
T è minorata da una
funzione divergente a +∞,
l’integrale improprio diverge. Quest’osservazione si usa confrontando la funzione
f(x) con
funzioni di “forma più semplice” il cui integrale si sa calcolare. Infatti:
Teorema 199 (di confronto per gli integrali impropri) Siano f(x)
e g(x)
localmente integrabili su [a, +∞).
Valga inoltre
0 ≤ f(x) ≤ g(x).
Allora: |
∫
a+∞g(x)dx < +∞⇒∫
a+∞f(x)dx < +∞;
∫
a+∞f(x)dx = +∞⇒∫
a+∞g(x)dx = +∞.
|
Siamo quindi ridotti a cercare delle funzioni di confronto
g(x)
abbastanza semplici. Ricordando che gli infinitesimi fondamentali di confronto per
x → +∞ sono
le funzioni
g(x) = 1
xγ
è naturale confrontare con queste funzioni, i cui integrali si calcolano
facilmente:
seγ≠1 ∫
aT 1
xγdx = 1
1−γ 1
Tγ−1 − 1
aγ−1
seγ = 1 ∫
aT 1
xdx = log T − log a
Dunque, si ha la situazione riassunta nella tabella 9.2.
Table 9.2: integrali impropri su una semiretta
0 ≤ f(x) ≤ M 1
xγ
γ > 1
∫
a+∞f(x)dx < +∞
f(x) ≥ M 1
xγ
γ ≤ 1 e M > 0
∫
a+∞f(x)dx = +∞
Inoltre,
Teorema 200 la funzione f(x)
(non negativa) abbia parte principale M
xγ
per x → +∞.
I due integrali impropri di f(x)
e di 1∕xγ
hanno lo stesso comportamento.
Dim. Infatti, l’ipotesi implica che M≠0
e inoltre
f ∼M
xγper x → +∞.
e quindi in particolare, per x
abbastanza grande, vale
1
2 M
xγ ≤ f(x) ≤ 2M
xγ. ■
Si noti che la condizione
0 ≤ f(x) < M 1
xγ
si verifica in particolare se f(x) è
(positiva ed) un infinitesimo per x → +∞,
di ordine maggiore di 1∕xγ.
Dunque,
Teorema 201 Se f(x) ≥ 0
ed inoltre per x → +∞
la funzione f(x)
è un infinitesimo di ordine maggiore di 1∕x1+𝜖
con 𝜖 > 0,
ossia
f(x) = o 1
x1+𝜖 per x → +∞ e con 𝜖 > 0 ,
allora l’integrale improprio
∫
a+∞f(x)dx
è convergente.
E’ importante notare che nell’enunciato precedente la condizione
𝜖 > 0
è cruciale. La condizione che f(x)
sia infinitesima di ordine maggiore ad
1∕x,
con esponente esattamente 1,
non implica la convergenza dell’integrale. Per esempio,
f(x) = 1
x log x = o 1
x
ma una primitiva di
1∕(x log x)
è
log(log x)
e quindi
lim T→+∞∫
2T 1
x log xdx = lim T→+∞log(log T) − log(log 2) = +∞.
9.5.2 Criteri di convergenza: funzioni positive su intervalli
Consideriamo il caso in cui f(x) ≥ 0
su (a,b], con asintoto
verticale x = a.
In questo caso, la funzione
𝜖↦∫
𝜖bf(x)dx
è decrescente e quindi dotata di limite per
x → a+, finito
o meno. E quindi si può ancora enunciare il teorema del confronto, come segue:
Teorema 202 (di confronto per gli integrali impropri) Siano f(x)
e g(x)
localmente integrabili su (a,b].
Valga inoltre
0 ≤ f(x) ≤ g(x).
Allora: |
∫
abg(x)dx < +∞⇒∫
abf(x)dx < +∞;
∫
abf(x)dx = +∞⇒∫
abg(x)dx = +∞.
|
Naturalmente, è ancora naturale scegliere come funzione di confronto gli infiniti campione
f(x) = 1∕(x − a)γ. Vale
anche in questo caso
Teorema 203 la funzione f(x)
(non negativa) abbia parte principale M
(x−a)γ
per x → a.
I due integrali impropri di f(x)
e di 1∕(x − a)γ
hanno lo stesso comportamento.
Quindi, va capito quando diverge oppure converge l’integrale improprio di
1
(x−a)γ.
E’ ancora vero che l’integrale improprio è divergente se
γ = 1, però ora le
due condizioni γ > 1
e γ < 1
hanno ruolo scambiato:
∫
ab 1
(x − a)γdx < +∞ seγ < 1,
∫
ab 1
(x − a)γdx = +∞ seγ ≥ 1.
Quindi, si può ancora dare una tavola analoga alla 9.2, ma con
versi delle disuguaglianze scambiate. Si veda la tabella 9.3 (dove
c > a e si intende che
f(x) è integrabile nel
senso di Riemann su [a + 𝜖,c]
per ogni 𝜖 > 0).
Table 9.3: integrali impropri su un intervallo
0 ≤ f(x) ≤ M 1
(x−a)γ
γ < 1
∫
acf(x)dx < +∞
f(x) ≥ M 1
(x−a)γ
γ ≥ 1 e M > 0
∫
acf(x)dx = +∞
Si noti che la condizione
0 ≤ f(x) < M 1
xγ
si verifica in particolare se f(x) è
(positiva ed) un infinito per x → +∞,
di ordine inferiore ad 1∕(x − a)γ.
Dunque,
Teorema 204 Se f(x) ≥ 0
ed inoltre per x → a+
la funzione f(x)
è un infinito di ordine inferiore ad 1∕(x − a)1−𝜖
con 𝜖 > 0,
ossia
f(x) = o 1
(x − a)1−𝜖 per x → a+ e con 𝜖 > 0 ,
allora l’integrale improprio
∫
abf(x)dx
è convergente.
Ripetiamo ancora che se f(x)
è un infinito di ordine inferiore esattamente ad
1 (ossia se nell’enunciato
precedente si ha 𝜖 = 0)
niente può affermarsi dell’integrale improprio di
f(x).
9.5.3 Il caso delle funzioni che cambiano segno
Ricordiamo le notazioni
f+(x) = max{f(x), 0},f−(x) = min{f(x)0}
cosìche
f(x) = f+(x) + f−(x),|f(x)| = f(x) − f−(x).
Dunque, se |f(x)|
ha integrale improprio convergente, anche le due funzioni
f+(x) e
−f−(x)
hanno integrale improprio convergente. E quindi la loro somma
f(x) ha
integrale improprio convergente. Si può quindi enunciare
Teorema 205 Una funzione localmente integrabile il cui valore assoluto
ha integrale improprio convergente, ha essa stessa integrale improprio
convergente.
E si noti che quest’asserto vale sia su semirette che su intervalli. In sostanza, questo è
l’unico criterio (ovviamente solo suffciente) di cui disponiamo per provare che una
funzione di segno variabile ha integrale improprio convergente: si prova che è
assolutamente integrabile (ossia che il suo valore assoluto è integrabile) usando i
criteri noti per le funzioni di segno costante. Se ne deduce che l’integrale improprio
della funzione converge.
9.6 Alcuni esercizi
- Si traccino i grafici delle funzioni
|
f(x) = sgn(sin x),g(x) = sgn(sin 2x),h(x) = sgn(sin 4x)
|
e si calcolino gli integrali su [0,π]
dei loro prodotti.
- Sia f(x) integrabile
su (−a,a) e dispari.
Si mostri che ∫
−aaf(x)dx = 0.
- Trovare una funzione pari e non nulla, tale che
∫
−aaf(x)dx = 0, con
a > 0.
- (⋆)
Se esiste, si trovi un esempio di funzione integrabile
f(x) ≥ 0, definita
su [0, 1], con
∫
01f(x)dx = 0. Può
essere che f(x)
sia continua? (Si ricordi il teorema di permanenza del segno).
- Sia f(x)
continua su ℝ,
con xf(x) > 0 per
x≠0. Mostrare
che f(x2)
ha integrale strettamente positivo su qualsiasi intervallo.
- Sia f(x) dispari e
continua su ℝ.
Mostrare che ∫
−11f(x3)dx = 0.
- Sia f(x)
integrabile su [a,b]
e non negativa. Si mostri che
a∫
abf(x)dx ≤∫
abxf(x)dx ≤ b∫
abf(x)dx.
E se f(x)
è negativa?
- (⋆) Si provi che
se f(x) è positiva
su ℝ e localmente
integrabile e g(x)
crescente, allora
H(x) = ∫
0g(x)f(s)ds
è crescente. Esaminare cosa può dirsi se
g(x)
è decrescente, e cosa può dirsi di
K(x) = ∫
g(x)0f(s)ds
- I due problemi seguenti sono formulazioni diverse dello stesso fatto:
- sia f(x) ∈ C1(0, +∞).
Calcolare
∫
abf′(t)f(t)dt.
- sia f(x)
continua per t ≥ 0.
Mostrare che per ogni t > 0
si ha
∫
0tf(s) ∫
0sf(r)drds ≥ 0
(è possibile che, con f(x)
non nulla, valga l’uguaglianza per un opportuno t > 0?
E per ogni t > 0?)
Sia f ∈ C(ℝ).
Mostrare che la disuguaglianza precedente vale anche se t < 0
intendendo l’integrale come integrale orientato.
- (⋆) Sia
f(x) monotona
crescente su ℝ.
Mostrare che esiste il limite
lim T→+∞∫
0T f(x2)dx.
Il limite può essere nullo?
- La funzione f(x)
sia positiva, con integrale improprio convergente su
[0, +∞). Si chiede di sapere
se può essere lim x→+∞f(x) = a > 0.
- (⋆) La
funzione f(x)
sia positiva, con integrale improprio convergente su
[0, +∞). Si chiede di sapere
se deve essere lim x→+∞f(x) = 0.
- (⋆)
Sia
f(x) = 1 sen − (1∕2n) < x < n
0 altrimenti.
Si disegni il grafico di f(x)
e (usando la formula (1.6)) si calcoli
∫
0+∞f(s)ds.
- (⋆)
Si dica se esiste una funzione continua e positiva, con integrale improprio finito su
[0, +∞), ma priva di
limite per x → +∞.
- Sia
∫
0+∞f(s)ds = L
(L
finito o meno). Calcolare
lim x→+∞∫
0x3(3+sin x)f(s)ds.
- Sia f(x)
una funzione per la quale converge l’integrale improprio
∫
−∞+∞f(x)dx.
Mostrare che
∫
−∞+∞f(x)dx = ∫
−∞+∞f(x + a)dx
per ogni a ∈ ℝ.
Cosa può dirsi se l’integrale improprio diverge oppure oscilla?
- Si mostri che ∫
0tf(t − s)g(s)ds = ∫
0tf(s)g(t − s)ds.
Spiegare come si trasforma questa formula se l’integrale è sull’intervallo
[a,t] con
a≠0 (incluso
il caso a = −∞,
supponendo la convergenza degli integrali impropri).
- (⋆) Si
considerino le funzioni definite all’esercizio 26 del Cap. 2, ossia le funzioni definite
su [0, 1]
da
fn(x) = 0 se0 ≤ x ≤ 1∕n
n se1∕n < x < 2∕n
0 se2∕n ≤ x ≤ 1.
Si calcoli ∫
01f
n(x)dx
e si consideri la successione di numeri
∫
01f
n(x)dx.
Se ne calcoli il limite e si rifletta sulla relazione, o mancanza di
relazione, che intercorre tra questa successione e il limite di
{fn(x)}, per
ogni x ∈ [0, 1],
calcolato all’esercizio 26 del Cap. 2.
- (⋆)
Una sbarretta di densità variabile è distesa sull’intervallo
[a,b] dell’asse
x. Sia
ρ(x) la densità del
punto di ascissa x.
In fisica, si definiscono massa e centro di massa della sbarra i due numeri
seguenti:
M = ∫
abρ(x)dx,x
0 = 1
M∫
abxρ(x)dx = 1
∫
abρ(x)dx∫
abxρ(x)dx.
Si provi che se ρ(x) = f″(x)
vale
x0 = bf′(b) − af′(a) −f(b) − f(a)
f′(b) − f′(a) .
- Sia f ∈ C(a,b)
e sia
S(x) = ∫
axxf(x)dx
∫
axf(x)dx ,∀x ∈ (a,b).
Usando la formula di L’Hospital si provi che
lim x→aS(x) = a;
ossia: il centro di massa di un segmento
[a,x] tende
ad a
quando la lunghezza del segmento tende a
0.
Appendix A
Glossario
- Limitazione superiore di un insieme significa “maggiorante”; per dire
“minorante” si dice anche limitazione inferiore
- Le notazioni seguenti si equivalgono:
sup{x,x ∈ A}, sup x∈A{x}.
Analogamente, si equivalgono
max{x,x ∈ A}, max x∈A{x}.
In particolare si potrà scrivere:
sup{f(x),x ∈ A}, sup x∈A{f(x)}; max{f(x),x ∈ A}, max x∈A{f(x)}.
- La notazione (xn)
indica la successione n → xn.
Il simbolo {xn}
può indicare sia la successione n → xn
che l’insieme degli elementi xn,
ossia l’immagine della successione. Talvolta una successione si indica col
simbolo xn,
senza parentesi, cosìcome si scrive f
per indicare la funzione x↦f(x).
- Abbiamo notato che le definizioni di limite si formulano in modo
unificato se si usa il linguaggio degli intorni. Però noi abbiamo preferito
specificare
“x → x0
con x0 ∈ ℝ
oppure x0 = +∞
oppure x0 = −∞”.
Si può abbreviare questa frase introducendo la notazione ℝ¯,
ove ℝ¯
indica l’unione di ℝ
e dei due simboli +∞
e −∞.
In questo modo, la frase tra virgolette viene compendiata dalla scrittura
α ∈ℝ¯.
Invece di ℝ¯
si usa anche il simbolo ℝ∗.
- Successione indeterminata o successione oscillante è una successione
priva di limite (per n → +∞).
Si noti che invece soluzione oscillante di un’equazione differenziale indica
una soluzione con infiniti cambiamenti di segno, anche se dotata di
limite, come per esempio e−x sin x.
- Funzione indeterminata (per x → α)
si usa per dire che lim x→αf(x)
non esiste.
- Il punto x0
si dice
- punto estremale,
- punto critico,
- punto singolare,
- punto stazionario,
- punto di stazionarietà
per una funzione f(x)
se è un punto interno al dominio di
f(x), la
f(x) è
derivabile in x0
e si ha f′(x
0) = 0.
I punti di massimo e di minimo (locali o globali) di
f(x)
si chiamano anche “estremi globali” o “estremi locali” della funzione. Fare
ben attenzione a non confonderli con gli estremi dell’immagine della
funzione!
- Si equivalgono i termini integrale definito ed integrale di Riemann.
- Sia (a,b)
un intervallo, limitato o meno. Una funzione si dice localmente integrabile su
(a,b) quando
è integrabile (nel senso dell’integrazione di Riemann) su ogni intervallo limitato e chiuso
[c,d] contenuto
in (a,b).
- Un integrale improprio si dice indeterminato quando non esiste il limite mediante
il quale esso è definito; ossia, se per esempio l’integrale improprio da considerare
è lim T→+∞∫
aT ,
quest’integrale è indeterminato quando il limite non esiste.
- Per indicare l’insieme delle primitive, invece di
∫
f(x)dx
si può anche scrivere
∫
f.
Per indicare l’integrale definito, invece di
∫
abf(x)dx
si può anche scrivere
∫
abf.
Simboli analoghi possono usarsi anche per gli integrali impropri.
|